数与形哪个先出现好

邹远容

人教版六年级上册《数学广角———数与形》中的第1个例题如图1所示。

教材上有两段对话，意在引导学生看图联系算式，体现数与形的结合。现在的问题是：呈现这个问题时，是先出现算式还是先出现图形？

我们设想先出现算式吧。

出示：1+3+5。教师说，算出结果太容易了，今天我們的任务不是算，而是用图形表示这个算式，然后从图形上看出结果。

好吧，用1个正方形表示1，2个正方形表示2，3个正方形表示3，如何将这些正方形组成一个图形呢？学生试着画，可能有下面的图形（如图2所示）。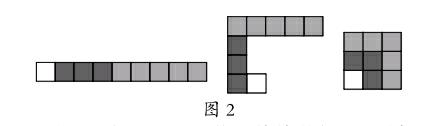

对这3个图形，要学生说说哪个图形最便于看出1+3+5的结果。学生的说法肯定不会相同，没关系。教师这时引导学生观察，第一个图没什么作用，需要一一数出来；第二个图中的方格横竖排列有重叠，容易数重复；第三个图是正方形，三种颜色的小正方形个数分别是1，3，5，一看就知道大正方形中方格有3×3=9（个）。通过这样的比较，学生会发现采用正方形表示1+3+5好。

为什么要设计这个环节？在教学实践中，教师往往直接说，我们可以用正方形表示1+3+5。虽然学生能够看懂，但对为什么只用正方形，而不用其他图形还是存在疑问的。教知识，有时有必要讲清知识教学的必要性，即为什么要学这个知识。有了前面的比较，学生就能发现采用正方形构图比其他图形优越———一看即明。进一步思考，就能得到以形表数的思路是：构造的图形能够将算式中的数及结果直观地用图表示出来。也就是说，图能够反映算式。

如果先出示图，再在图上找算式1+3+5，又会怎样呢？

如果从图上找算式，可以找出很多个，一时还难以想到1+3+5。比如，第三个图，肯定有学生会找出3+3+3，也会有学生找出1+2+3+2+1。这两个算式很有规律，你不能说错呀。这时，教师只能从众多算式中挑出1+3+5，转到教学内容上来。

由此可见，教材这个内容，重点应该在由数构形。由数构形重在思考构什么样的形，才能将算式很直观地在图上反映出来，而且算式的结果也能够从图上看出来，不要进行复杂的计算。这是构形的基本要求。

为了让学生进一步理解构形的要素，还可举下面的例子。