“三位数乘两位数”教学研究报告
2017-05-20
一、问题
人教版四年级上册第三单元三位数乘两位数是小学阶段整数乘法模块的最后一个内容。如果理解了两位数、三位数乘一位数的乘法竖式是对加法竖式的简写,两位数乘两位数的乘法竖式记录“用乘法分配律进行演算的算理”的一般原理,我们就不难看出三位数乘两位数的计算与两位数乘两位数的计算并无本质上的区别。显然,三位数乘两位数的教学目标不再是掌握原理本身,而是同一原理的运用:学生能根据两位数乘两位数的笔算方法,类推并掌握三位数(多位数)乘两位数的笔算方法。从这个角度看,与两位数乘两位数相比,三位数乘两位数更容易被学生理解与接受,但计算难度高于两位数乘两位数。
(一)教学实践中的问题
在学习三位数乘两位数之前,为了了解学生的相关知识和经验,保证教学活动的科学性和有效性,我们随机抽取了三年级刚学完两位数乘两位数的62名学生进行了学前检测。从前测看,大部分学生已经掌握了两位数乘两位数的算理。即便是没有学过三位数乘两位数,59.7%的学生能够自觉迁移两位数乘两位数的方法,顺利得出计算结果。
同时,我们对相关教师进行了问卷调查与访谈,部分老师认为学生不难获得三位数乘两位数的方法。但是由于计算教学的训练单调枯燥,学生的学习热情不高,消极应对,计算准确率低;教材中计算器的引入导致学生更加不重视三位数乘两位数的笔算,认为大数据应该由计算器完成。此外,计算教学过分强调精确计算,忽视估算能力的培养;过分追求算法多样化而影响了课堂教学的效率等,都是老师们在教学实践中遇到的真问题。
(二)解决问题的策略
对于老师们在教学实践中发现的这些问题,在进行教学设计时,我们进行了有针对性的研究,认为可以采用如下的策略进行教学实践。
1.问题引领,促进算理正迁移。
波利亚说:“如果我们成功地回想起一个与当前问题密切相关的问题,那是很幸运的。我们应当争取这样的运气。”设置“与当前问题关系密切”的问题显然是学生顺利进行正迁移的重要途径。那么,与三位数乘两位数非常密切的是两位数乘两位数。因此教师可以引导学生思考:与两位数乘两位数相比,今天的问题有什么不同?能不能利用两位数乘两位数的竖式解决?
2.任务诱发,促进算法的优化。
有人把口算、笔算、估算称为“计算三宝”。要让学生认识到不同的计算方法的适用性,在学习中感受到计算方法学习的乐趣,掌握运用“计算三宝”解决数学问题,教师可以精心设计问题、习题,用具体任务驱动学生的数学思考。
3.情境驱动,促进运算自动化。
运算技能的形成阶段论将运算技能的形成分为认知阶段———联结阶段———自动化阶段,在这里也就是指小学生学习计算时经历探索、习得计算法则的阶段(如两位数乘两位数笔算时的程序化),到尝试运用法则独立进行计算的阶段,再到熟练掌握并灵活运用法则的阶段(如三位数乘两位数的笔算)。心理学研究表明,当个体进入计算自动化阶段以后,他们的运算速度和正确率就会大大提升。要帮助学生的运算技能实现自动化,教师可以把枯燥的计算融入到各种有趣的情境中,使学生乐在其中,在不知不觉中增加训练,提升计算技能。
二、实践
基于以上的思考,我们在教学三位数乘两位数时进行了尝试,意图让学生在问题的驱动下自由穿梭在各种算法中,水到渠成地达到训练计算技能、涵养理性精神的目标。
教学过程:
1.巧设问题练口算
师:孩子们,今天这节课我们将举行一场有趣的计算竞赛。我们一起加油吧!请听规则———在下面的7道算式中,找出能口算出得数的算式,然后算出得数,想一想你是怎样算的。(课件出示:576×39,400×27,310×52,206×30,520×40,45×57,408×25)
生1:我覺得400×27,206×30,520×40可以口算。
(师引导学生说清算理,强调中间和末尾有0的情况,组织评价)
生2:408×25也可以口算,我知道乘25的速算规律,只要看408里面有几个4,得数就是几个百。
师:太厉害了,真是计算高手!
2.比较大小学估算
师:在剩下的3个算式中,不动笔计算,你能看出哪个算式的得数最大,哪个算式的得数最小吗?为什么?
生3:得数最小的算式是45×57。因为45×57是两位数乘两位数,而其他的算式是三位数乘两位数。
生4:我也认为45×57的得数最小,但是他说两位数乘两位数的结果一定比三位数乘两位数的小是不对的,80×50不是比100×10大吗?
师:你很会说理,举例子的确是一种说理的好方法。你是怎么知道45×57的得数最小的呢?
生4:我估算出45×57大约是3000,而其他算式的得数都大于15000。
师:他采用估算的方法,真不错!不过,老师有点好奇的是,老师还没教三位数乘两位数(板书课题),你怎么就会估算了?
生4:我想三位数乘两位数的估算和两位数乘两位数的估算,道理是一样的。576×39中,576大于500,39大于30,得数肯定大于15000;310×52中,310大于300,52大于50,得数也肯定大于15000。
师:真是会学习的孩子。他从两位数乘两位数的估算中学会了这么多道理。那么,在剩下的2个算式里,哪个的得数更大呢?
生5:576×39的得数比15000大得多,而310×52的得数更接近15000。
3.精确比较学笔算
师:576×39,310×52的得数都比15000大,如果我想知道到底大多少,怎么办?
生:那就笔算!用计算器也可以!
师:那我们先笔算,然后用计算器检验,如何?(可以!)这么快就同意了,三位数乘两位数的笔算老师还没教呢!
生:和两位数乘两位数的笔算方法一样嘛!
师:好样的,试试吧!
学生笔算后,同桌交流算法。师指名上台展示讲解,教师及时追问并板书每一部分积的意义(如图所示)。
师:谁还有问题吗?
生6:310×52笔算时可不可以把末尾的0放在一边呢?
生7:应该可以的,0乘任何数都得0,乘完0前面的数,在积的最后添上0就行了。
学生练习,指名板演(如图所示)。
师:通过笔算,我们知道了576×29的积确实大于310×52的积。三位数乘两位数的笔算,老师没有教你们就会了,真棒!如果是四位数乘两位数的笔算,你们还会吗?如果是四位数乘三位数呢?
生8:会啊!一样的道理嘛,只是多了一位数。
生9:四位数乘三位数,积应该有三层,第三层积的右边第一位要和百位对齐。
师:我想,“举一反三,触类旁通”就是专门用来表扬你们这种孩子的!
4.灵活运用各算法
师:谁能用310×52中的5个数字编一道三位数乘两位数的题,每个数字不能重复,积比310×52小?
学生小组活动,得到的算式有:125×30,230×15,105×23,203×15,235×10。
师:在这些算式中,哪个算式的积最小?
生10:我们认为最小数占最高位的积会比较小,125×30的积比其他算式的要大。
师:你说得有道理。剩下的算式又怎么判断?
生11:我们认为235×10的积最小,是2350;而203×15只要把203估成200,积比3000大,明显比2350大;105×23也比100个23多5个23,肯定比2350大;230×15的积也比3000大。
师:大家笔算105×23,检验你们的判断是否正确。刚才我们玩了最小的,现在换个玩法———玩最大的。在所有三位数乘两位数的算式中,最大的一个是多少?(999×99)不计算,你知道它的得数是几位数吗?为什么?
生12:这个算式的得数是五位数。因为1000×100=100000,这是一个最小的六位数,而999×99比它小,所以得数应该是个五位数。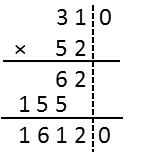
生13:我把99估成100,因为999×100=99900,实际结果比这个数要小,肯定是个五位数。
师:真是精益求精,掌声送给计算高手!下面是四(2)班三位同学的作业,他们算得对吗?说说理由。甲:999×99=98999;乙:999×99=99901;丙:999×99=98901。
学生观察、思考,然后汇报。
生14:第一个算式个位上是9乘9,积的个位不可能是9,所以甲的答案肯定是错的。
生15:第二个算式中99估成100都只有99900,积不可能大于它,所以乙的答案也不对。
生16:丙的答案不能一眼看出来,我们可以笔算。
……
师:孩子们,你们今天的表现让老师倍感欣喜,你们的创造力远远超出了我的想象!
5.追根溯源释算理
师:在很早以前,我们的祖先们是怎样笔算乘法的呢?(课件出示:据《算法统宗》一书记载,中国明朝时期还没有出现乘法竖式这种计算方法,古人都是用“铺地锦”的方法计算乘法。)关于“铺地锦”,你想了解些什么呢?请同學们看书,上面介绍的“格子乘法”就是“铺地锦”算法。(学生阅读)你知道怎样用“铺地锦”的方法计算了吗?
学生质疑,相互答疑。
师:“铺地锦”是古代阿拉伯人计算乘法时用的一种方法,后来传入我国,因为计算完了以后,形如我国古代织出的铺在地上的锦缎,人们将这种计算称为“铺地锦”。感兴趣的孩子课后可以用“铺地锦”的方法研究462×34。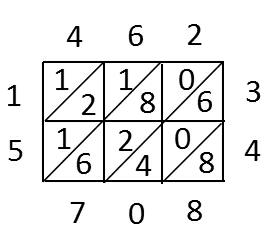
设计意图综述:三位数乘两位数与两位数乘两位数,内容看起来差不多,但却各有其独特的教育功能和价值。本节课遵循因材施教理念,即因教材而教,把促进正迁移、促进计算技能形成、促进思维训练作为主要目标,努力实现计算教学应该承载的技能习得、心智培育、习惯培养等育人价值。
1.促进正迁移。知识迁移就是人们已有的认知结构对新知识学习发生影响。本节课中,教师设计开放的问题情境,让学生自动唤醒两位数乘两位数的计算经验,自觉地建立新旧知识的关联点,并迁移到三位数乘两位数的学习中。因不教而会,学生自然会体验到学习带来的成就感。
2.促进计算技能形成。计算技能的形成离不开练习。教师需要创设高质量的问题情境,使学生能安安静静地思考、安安静静地练习。本节课中,学生在教师设计的情境中进行了口算、估算、笔算,积累了计算经验,有利于形成扎实的计算技能。
3.促进思维训练。对学生进行思维训练是数学教学的重点也是难点。本节课中,教师设计的“比最小”“比最大”等教学活动都是很好的训练数学思维的活动。学生在参与的过程中,大脑皮层始终保持最活跃的状态,联系、类比、假设等思维活动贯穿课堂始终,学生的心智水平也因此得以提升。
三、讨论
1.学生计算水平整体下滑带来的思考
计算教学一直是我国小学数学教学中的一个重点。新课标实施以前,大纲对学生計算能力的要求是“准确、快速、灵活、简便”。老师们常常通过一些程式化的计算教学和大量的机械训练使学生达到这个目标。由于这种简单操练没有充分实现计算教学的教育功能和培育学生素养的价值,久而久之,很多老师和孩子对计算教学活动失去了兴趣,都希望能从这种机械模仿中解放出来。
随着计算机和计算器的普及,越来越多的人认为:对学生来说,知道什么时候需要哪种计算方法,比拥有熟练的计算技能更有价值。对大数据的精算,更是可以采用现代化计算工具代劳。同时,新课标也对计算教学提出了新要求,提倡设计生动有趣的学习活动,激发学生的学习兴趣,重视数学思维能力的培养。但是在实施过程中,老师们发现学生的计算水平整体下滑趋势非常明显,计算正确率降低、口算速度减慢现象普遍存在,学生对计算的兴趣似乎也没提高多少。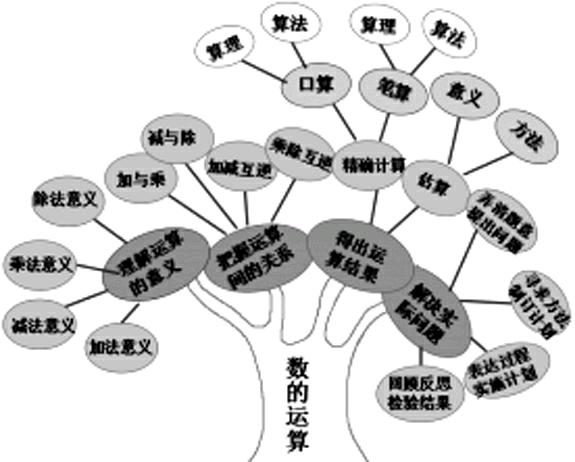
我们认为,培养学生学习数学的兴趣,不能以牺牲学生的计算能力为代价,而应该对学生的计算提出清晰的要求,规范、认真、细致、准确、灵活等都是计算教学需要秉承的原则。在计算教学实施中,老师们如何正确运用教学策略,既落实计算基本功的训练,又能最大限度地调动学生的学习积极性,发挥计算教学的育人功能,值得我们一线教师不断思考与践行。
2.计算教学与解决问题的联系
数的运算一般按照理解运算的意义、把握运算间的关系、得出运算结果、解决实际问题四个部分进行教学。右图的“知识树”很好地概括了数的运算板块各内容之间的结构关系。
人教版教材中将得出运算结果、解决实际问题这两个内容结合起来教学,旨在把计算教学融入到应用中,让学生利用问题的现实背景经历算法的探索过程,在解决问题中认识计算的工具性作用和解决实际问题的价值。但是,我们在进行三位数乘两位数的教学设计时,发现例1的实际问题中,学生体会不到估算的必要性。于是,我们舍弃了例1,选择了7个简单的乘法算式,通过问题的设计和教学情境的设置,激励学生自主参与算理的回顾迁移、计算方法的灵活选择与计算技能的训练,把常见的数量关系的教学移到了下一课时。这种取舍也留给了我们一些思考:教师如何认真研讨教材,做到因材施教,即准确把握什么样的内容承载什么样的教育功能,实现什么样的教学目标,什么样的教学策略能使计算教学带来最大的效益,值得我们不断实践与探索。
(本文系湖南省教育科学“十二五”规划2014年度立项课题(编号:XJK014CZXX041)研究成果)
(执笔:邓求平、谢加文、刘硕鹏、戴益祥、王志林、王丽燕、徐旺、李闯)
