SOP算法在抗干扰卫星导航天线中的应用

唐洪军

(中国电子科技集团公司第10研究所 共性技术部，四川 成都 610036)

SOP算法在抗干扰卫星导航天线中的应用

唐洪军

(中国电子科技集团公司第10研究所 共性技术部，四川 成都 610036)

抗干扰算法研究是解决卫星导航天线易受干扰问题的重要途径，针对常用的LMS算法收敛速度慢的缺点，采用子空间正交投影算法，其忽略噪声的扰动影响，在干扰比噪声功率稍大的情况下，方向图对干扰噪声比是鲁棒的，并且在不先行得到干扰来波方向的情况下，直接对干扰形成零点。通过仿真与LMS算法进行比较，SOP算法具有更快的收敛速度。

卫星导航；抗干扰；自适应阵列；LMS算法；间正交投影

随着卫星导航的广泛应用，许多武器装备平台对卫星导航的依赖度增加，卫星导航的应用将大幅提高武器装备平台或武器打击的自主性、精确性和实时性[1]。战争实践证明，现代战争精确快速的定位和导航是提高武器的命中精度及杀伤力的关键因素。因此，卫星导航在军事指挥、控制、通信、计算、情报、监视和侦察系统方面也成了重要的组成部分，是精确指挥控制、精确打击和精确兵力部署的关键支撑系统。民用方面，卫星导航也已经广泛应用在交通运输、测绘资源勘探、科学研究、土建工程、社会治安医疗急救等领域。

但卫星导航信号本身比较弱，比环境噪声还低30 dB，普通的广播信号也可能对其造成干扰。随着无线电的广泛应用，空间电磁环境复杂，特别是在战争中，有针对性的人为干扰更能影响接收机的正常工作[2-3]。当导航接收机受干扰而无法工作时，导航技术的所有优势及便利则无从谈起。在强干扰环境下，自适应调零天线是提高卫星导航接收机抗干扰能力的有效措施[4]。自适应算法作为抗干扰卫星导航天线的核心，对其进行深入研究将促进卫星导航抗干扰技术的发展，具有一定的研究价值[5-6]。目前常用的抗干扰算法为LRM算法，但其收敛速度较慢，本文采用SOP(Subspace Orthogonal Projection，SOP)算法对LRM算法进行改进，并对两种方法进行对比。

1 抗干扰天线基本原理

自适应调零天线以自适应天线技术为基础，将若干独立的天线阵元的输出自动地组合起来，采用自适应算法来形成方向图，使进入接收机系统的总输入功率降至噪声电平大小，可以有效抑制信号电平高于噪声水平的干扰。从空间响应看，自适应调零天线是一个空间滤波器，它实际上是实现阵列方向图的空域调零，在天线阵的方向图中产生对着干扰源方向的零点，以减低干扰源的效能[7]。

自适应调零天线的核心部分为自适应波束形成器，依据权值在模拟信号上调节或在数字信号上调节的不同，可分为模拟波束形成和数字波束形成两种[8-9]。以数字波束自适应调零天线为例，其系统组成如图1所示。射频信号被天线接收，经带通滤波和下变频后，变为低中频或者基带信号，再被ADC数字化后送入波束形成器。波束形成器根据接收到的信息，以功率最小化为准则自适应地加权各个通道送入的信号，相加合并后输出[10-13]。

图1 自适应调零天线系统

波束形成器权值计算的基本过程是：先建立系统的数学模型，在描述系统中各处的信号后，根据系统的性能要求，将信号组合或分配表述为一个数学问题，寻求其最优解[14]。

假设接收天线为M元均匀线阵，相邻阵元之间的间隔为Δd，且各阵元各向同性，对各阵元的加权分别为w1,…,wm。入射信号s(t)是窄带信号，载波波长为λ，从俯仰角φ平面波形式入射，如图2所示。

图2 信号入射在线阵上的示意图

M阵元阵列中第m阵元收到的信号为

(1)

其中，τi(φ)为阵元i收到信号相对参考点的入射波时间延迟。在入射信号窄带情况下

si(t-τi(θ))≈si(t)

(2)

那么接收到的信号可以向量表示为

x(t)=[x1(t),…,xm(t)]T=s(t)·VT(φ)

(3)

其中，T代表转置运算；xi(t)为第i个单元通道接收到的信号；V(φ)为的阵列响应矢量，与阵面上阵元分布和窄带平面波信号入射角度有关

(4)

接收信号经数字化后，信号可用向量X(n)来表示。在无噪声情况下，加权后天线阵的输出为

Y(n)=WHX(n)

(5)

上标H表示求共轭转置运算。在考虑噪声N(n)时，用

X(n)=s(n)V(n)+N(n)

(6)

代替前面的X(n)。为使输出平均功率最小，可以通过调节权值W实现

(7)

其中，E{·}为求期望运算。

2 抗干扰算法分析

工程应用中通常使用LMS算法来实现权值计算，但LMS算法收敛速度慢是制约系统指标的关键因素，并且当干扰信号间的空间相关性很大时会使算法收敛速度变慢[15]。当卫星接收机对抗干扰的实时性能要求高时，由于LMS算法收敛速度的限制，有时LMS算法就不能满足要求。针对该问题，提出一种以特征值分解为基础的正交子空间投影算法，即SOP算法。

假设天线为N元阵列，接收信号为X=[x1,x2,…,xN]T，记W=[w1,w2,…,wN]T为阵列的加权矢量，δ0GPS为假定的无干扰时的导向向量。那么天线输出为Y=WHX，输出功率P=Y*Y。为保证卫星导航信号的单位增益，那么线形约束功率最小准则可表示为

(8)

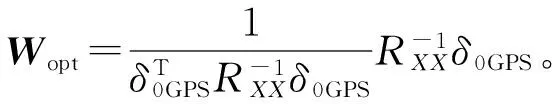
(9)

其中，Sk(t)、Jk(t)和N(t)分别为第K个GPS信号、第K个干扰信号和各阵元的热噪声；δGPS、δJ为GPS信号和干扰信号的方向矢量，对于N-1个阵元均匀分布在圆边，1个阵元位于圆心的阵列分布，当来波方向为俯仰角θ，方位角φ时，天线的响应方向矢量

当各卫星信号和干扰信号之间不相关时，由RXX=E[X(t)XH(t)]式得

(10)

(11)

它可正交化为

(12)

其中，λk和ek(k=1,2,…,D)为对应第k个干扰信号的特征值和特征向量。

(13)

在干扰功率远大于噪声电平时

(14)

那么最优权

(15)

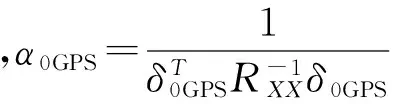
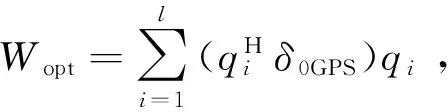
相关矩阵的大特征值的对应特征向量与高于噪声电平的干扰信号的导向向量相关，利用该特性，SOP算法可以忽略噪声的扰动影响，直接对干扰形成零点，因为它移除了噪声量的影响，使得干扰比噪声功率稍大的情况下，方向图对干扰噪声比是鲁棒的。SOP算法可以在未得到干扰来波方向的情况下，产生正对干扰的零点，避免了对卫星导航信号来波方向判断的依赖。同时，与LMS算法相比，SOP算法有更快的收敛速度，它与SMI算法有相同的收敛速度量级，与干扰来波方向和噪声无关。

3 仿真分析

假设两个干扰分别来自(20，40)(30，-140)方向，SOP算法的收敛情况和方向图，如图3所示。

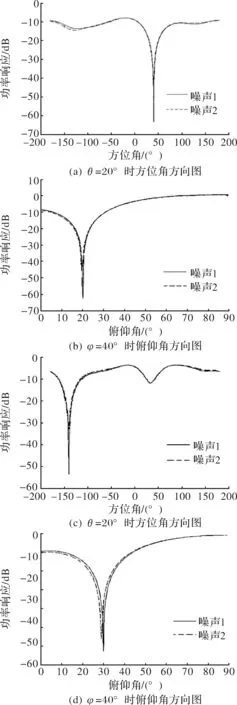
图3 SOP算法所得的方向图

图3(a)～图3(d)中，分别给出了两种噪声电平下的天线方向图，其中噪声2的电平比噪声1的电平高20 dB，由图可见两条曲线有较好的重叠，方向图对噪声是鲁棒的。

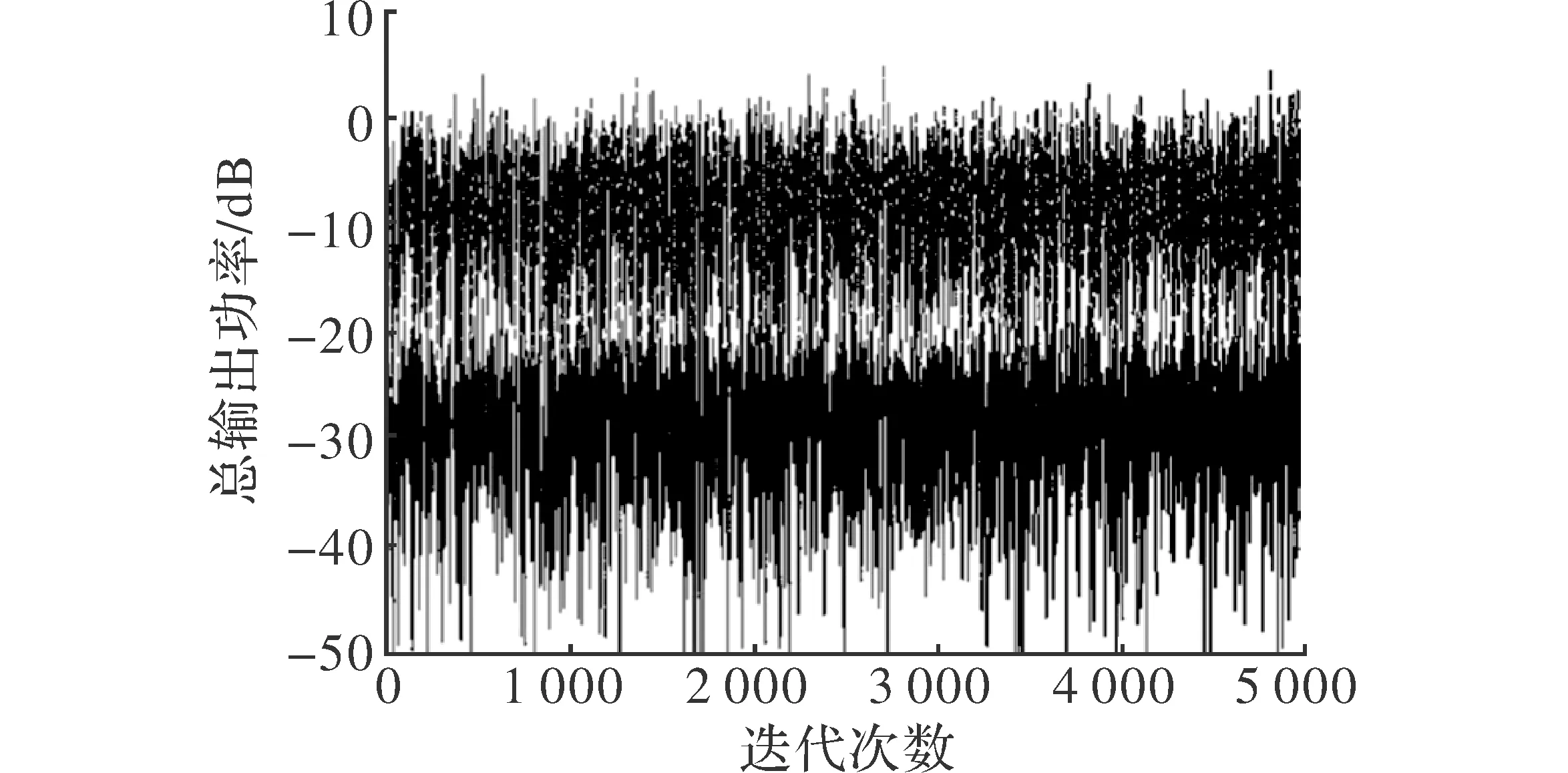
图4 SOP算法所得的收敛曲线

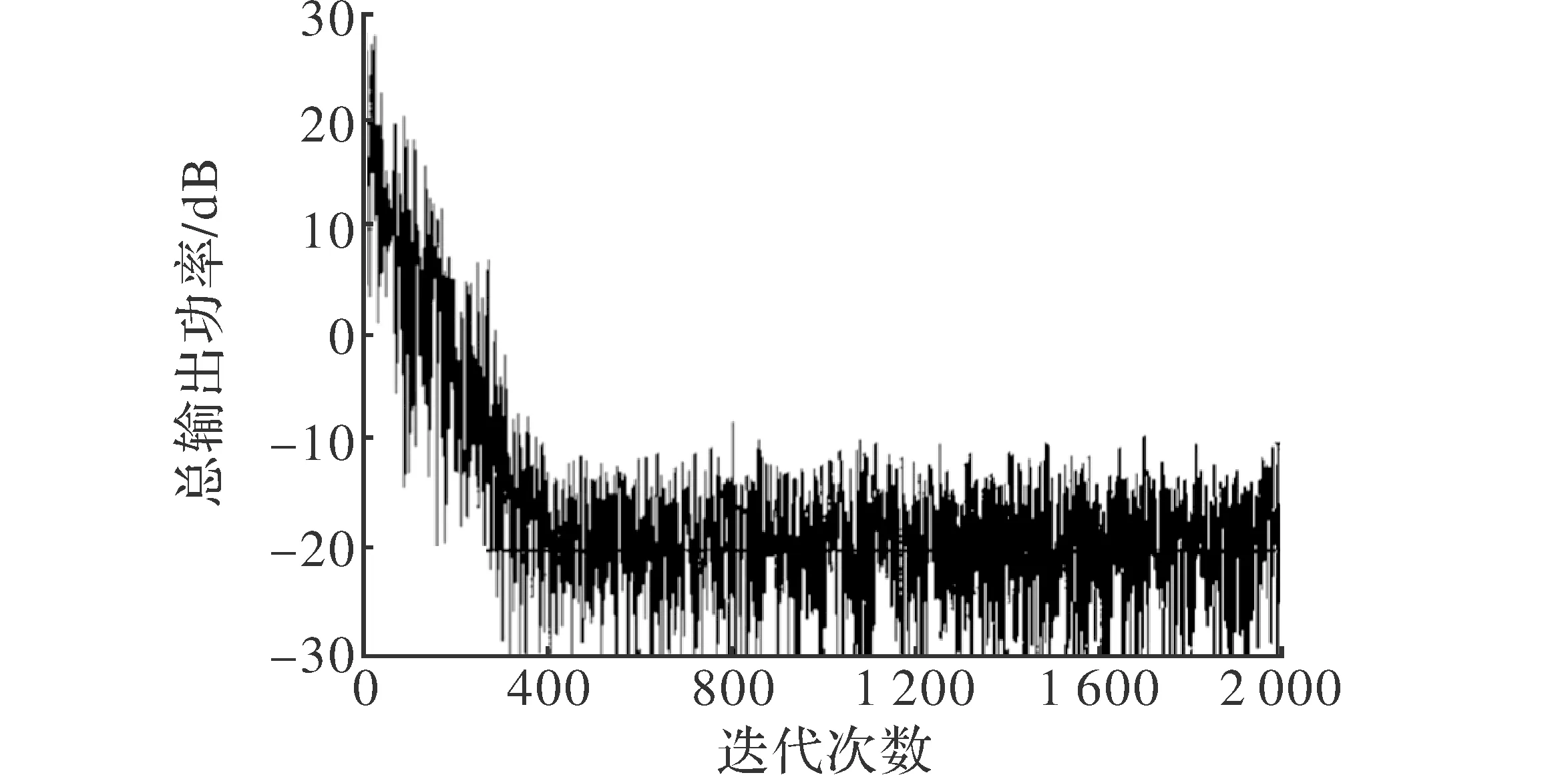
图5 LMS算法所得的收敛曲线

图4和图5分别是SOP算法和LMS算法所得的总功率随着采样次数的收敛曲线，其中图4中分别给出了两种噪声电平下的收敛情况，上面曲线的噪声电平比下面曲线的噪声电平高20 dB。对比图4和图5可以看出，SOP的功率曲线收敛不同于LMS算法，需要多次采样迭代后收敛，SOP算法有更快的收敛速度。

4 结束语

相关矩阵的大特征值的对应特征，向量与高于噪声电平的干扰信号的导向向量相关，利用该特性，SOP算法可以忽略噪声的扰动影响，直接对干扰形成零点，因为它移除了噪声量的影响，使得在干扰比噪声功率稍大的情况下，方向图对干扰噪声比是鲁棒的。SOP

算法可以在不先行得到干扰来波方向的情况下，产生对着干扰的零点，避免了对卫星导航信号来波方向判断的依赖。同时，SOP算法的收敛速度比LMS算法更快，并与干扰来波方向和噪声无关，可以应用在自适应抗干扰的卫星导航天线中。

[1] 边少峰,李文魁.卫星导航系统概论[M].北京:电子工业出版社,2005.

[2] 宋颖凤,葛海龙.对GPS的干扰与抗干扰技术研究[J].舰船电子工程,2004,24(6):26-30.

[3] 郭艳丽,林象平.GPS抗干扰技术浅析[J].航天电子对抗,2001(6):23-26.

[4] 王运东,徐锦,李军,等. GPS接收机系统的抗干扰技术[J].船舶电子工程,2006,26(3):31-35.

[5] 石镇.自适应天线原理[M].北京:国防工业出版社,1991.

[6] 崔玥.卫星导航系统接收机抗干扰技术研究[D].天津:天津大学,2012.

[7] Widrow B.Adaptive antenna systems[J]. Proceeding of IEEE,1967(55):143-2159.

[8] 王超,吴德伟.自适应调零天线GPS抗干扰技术研究[J].全球定位系统,2003,28(6):15-17.

[9] Brown A, Morley D. Test results of a 7-element small controlled reception pattern antenna[C]. CA,USA:Proceedings of Ion Gps, 2001.

[10] Ly H, Eyring P, Traum E, et al. Design, simulation, and testing of a miniaturized GPS dual-frequency (L1/L2) antenna array[C]. MA,USA:Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2002.

[11] Zeng H,Zeeshan A,Dong T,et al.Null steering antenna beamforming utilizing space-time adaptive processing[J].Journal of China Universities of Posts & Telecommunications,2015,22(4):51-55.

[12] Zoltowski M D, Gecan A S.Advanced adaptive null steering concepts for GPS[C].UK:Military Communications Conference, 1995.

[13] Wang L J,Xu J M. The simulation analysis and experiment results of null steering antenna for GPS receiver[C]. Lanzhou:Proceedings of the 6th International Conference on Wireless Communications Networking and Mobile Computing,2010.

[14] 卢昕,熊昌仑，郑建生,等.基于DSP技术的GPS接收机天线自适应抗干扰模块的设计与实现[J]．武汉大学学报:信息科学版,2005,30(7):654-657.

[15] 晋军,王华力,段涛,等.混合遗传算法用于卫星自适应调零天线研究[J].通信学报,2006,27(8):35-40.

Application of Subspace Orthogonal Projection in Satellite Navigation Receiver Antennas

TANG Hongjun

(Common Technology Department, 10th Research Institute of CETC, Chengdu 610036, China)

Ante-interference algorithm is important for satellite navigation’s vulnerability to interferences. Since the LMS converges slowly, the SOP (subspace orthogonal projection) algorithm has been used. Because the turbulence of noise has been ignored, the antenna pattern is robust to the interference noise ratio when it is large. And SOP can get a null beam on the direction of interference. Simulation results in comparison with LMS show that SOP has faster convergence.

satellite navigation; anti-interference; adaptive array; LMS; subspace orthogonal projection

2016- 06- 14

唐洪军(1983-)，男，工程师。研究方向：信号处理。

10.16180/j.cnki.issn1007-7820.2017.05.033

TN967.1

A

1007-7820(2017)05-120-04