基于PCA-ELM的模拟电路故障诊断

周江嫚

(武汉烽火富华电气有限责任公司，湖北 武汉 430000)

基于PCA-ELM的模拟电路故障诊断

周江嫚

(武汉烽火富华电气有限责任公司，湖北 武汉 430000)

针对模拟电路的故障诊断，提出一种基于主元分析与极限学习机相结合的方法。该方法利用主成分分析法对提取的特征数据进行降维，再结合极限学习机对电路故障进行分类。主元分析具有数据压缩及特征提取的优点，极限学习机学习速度快、泛化性能好。实验结果表明，采用PCA-ELM结合对故障数据处理，故障诊断分类的准确性可达98.3%以上。

模拟电路；故障诊断；极限学习机；主元分析

随着电子设备的广泛应用，其电路设计也愈加复杂，电路故障的快速诊断和准确定位就成为研究热点。由于电路集成度增加、输入输出均是连续量、电路元件参数具有容差性、且存在反馈回路和非线性问题[1-2]，使得模拟电路的故障诊断异常复杂，技术发展缓慢。

故障字典法等传统模拟电路故障诊断方法，因其局限性已逐步被机器学习方法所代替。其中基于神经网络的故障诊断方法目前在国内外研究较为广泛，如基于小波神经网络的方法[3-4]、基于BP及SVM神经网络的方法[5-7]、基于支持向量机的方法[8]以及基于神经网络和模糊理论的方法[9]，主元分析和神经网络相结合的方法[10]等。但这类方法普遍存在着对学习样本要求高、模型结构和参数难以优化等局限性，且至今仍未得到很好的解决。近年来，由G B Huang提出的极限学习机(Extreme Learning Machine，ELM)[11-14]因其学习速率快和泛化能力好，开始在故障诊断中得到应用，并显示出良好的应用前景。

在实际的故障中，原始的故障数据中会包含很多与故障特征不相关的变量信息。而这些变量会影响分类器性能，同时也增加了计算量，导致实时性变差，因此需要对原始样本进行适当的降维处理。本文提出一种基于主元分析与极限学习机相结合的模拟电路故障诊断方法，先利用主元分析法(Principal Component Analysis，PCA)提取样本集的主元，得到故障特征，然后利用ELM对特征向量进行分类，实现故障诊断。实验结果表明，该方法分类准确率高、推广能力好，能够实现模拟电路故障的快速检测与准确定位，并具有较高的鲁棒性。

1 基于PCA的故障特征提取

1.1 主元分析

故障检测的首要问题就是对可测信号进行故障特征提取，即对信号进行处理，从而获取反映故障信息的特征。通常，从待测电路的响应曲线获得原始数据，通过对原始数据进行采样，可将原始数据映射成为样本空间中的点。但由于这些数据包含了很多与故障特征不相关的信息，因此需要对这些数据进行预处理。

主元分析是通过对多变量进行降维的一种数据现行组合方法，它在尽可能保留原有信息的基础上，而且彼此互不关联，使其能更集中地反映原来变量中所包含的变化信息。变量的主成分分析，可以观察到变量在主成分上的分布，通过对各个变量在主成分上的载荷因子大小找出影响结果的重要变量，进而选择主要表征变量[10]。通过主成分分析，可以减少神经网络的输入参数的维数量，同时加快了网络的收敛，也起到了去噪的作用。它克服了由于非线性等不易建立精确数学模型的缺点，正日益受到关注。

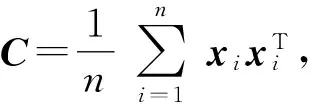
1.2 特征提取

模拟电路中不同故障情况下的输出响应与正常情况下的输出响应相比，在同一频率会有较大的差别，因此各频率响应中包含了丰富的故障信息，构成了反映故障特征的原始数据。利用主元分析对这些样本提取故障特征，较大程度反映了故障特征，降低了空间维数，更利于模拟电路的故障分类。

建立主元模型和进行特征提取的具体步骤是：

(1)原始数据标准化。设原始数据样本为X∈Rm×n，其中，m为样本数量；n为特征值的数量。对其进行标准化的方法是

(1)

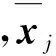
(2)建立样本的协方差矩阵，并求其特征值及其特征向量

(2)

式中，Λ=diag(λ1,λ2,…,λn),且λ1≥λ2≥…≥λn，U=[u1,u2,…,un]是与特征值相对应的标准正交特征向量组成的矩阵；

(3)计算前p个主元的累积贡献率η(p)，选取主成分

(3)

累积贡献率用于衡量新生成分量对原始数据的信息保存程度,通常要求其大于85%即可；

(4)取前p个较大特征值对应的特征向量构成变换矩阵P

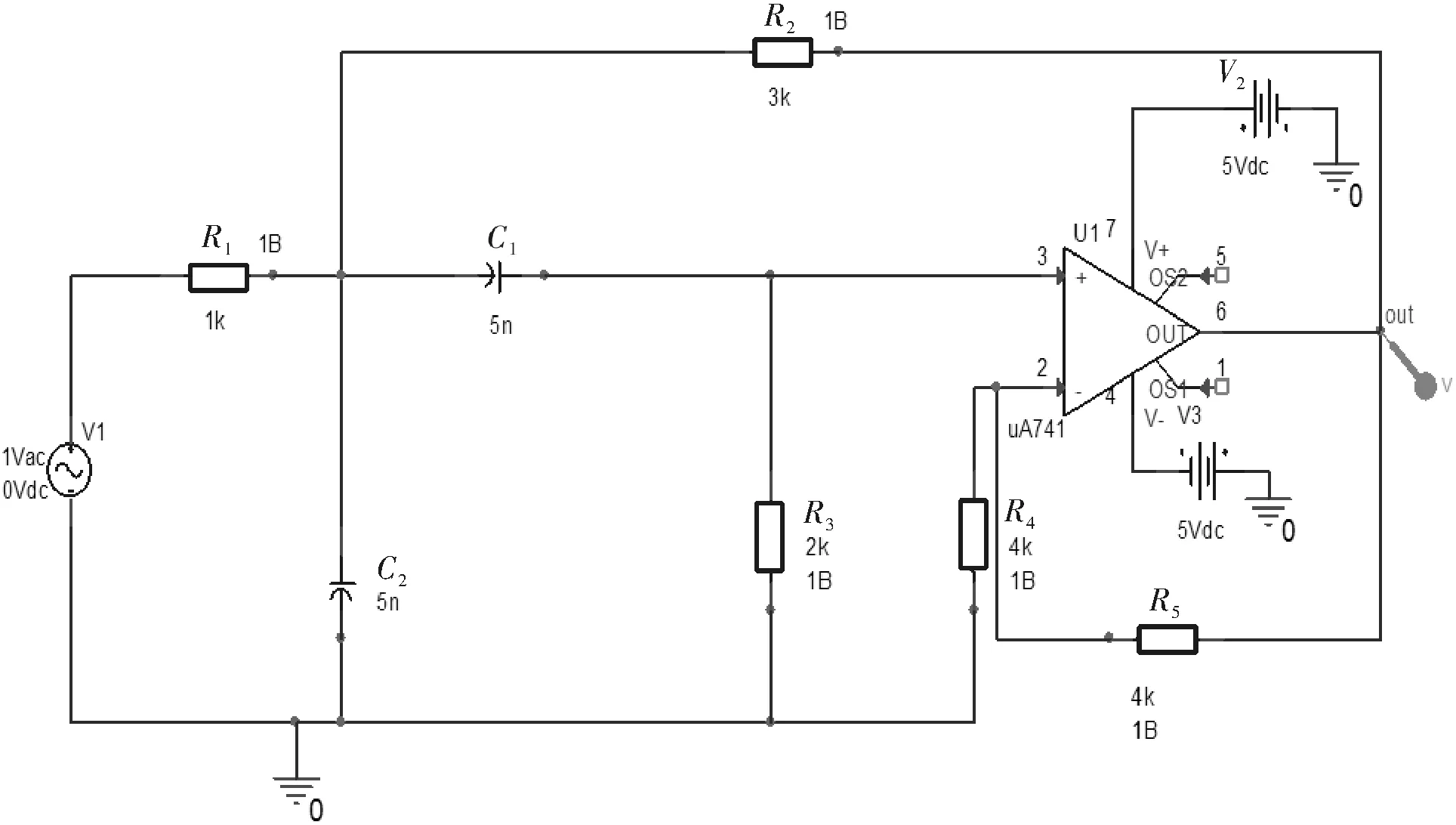
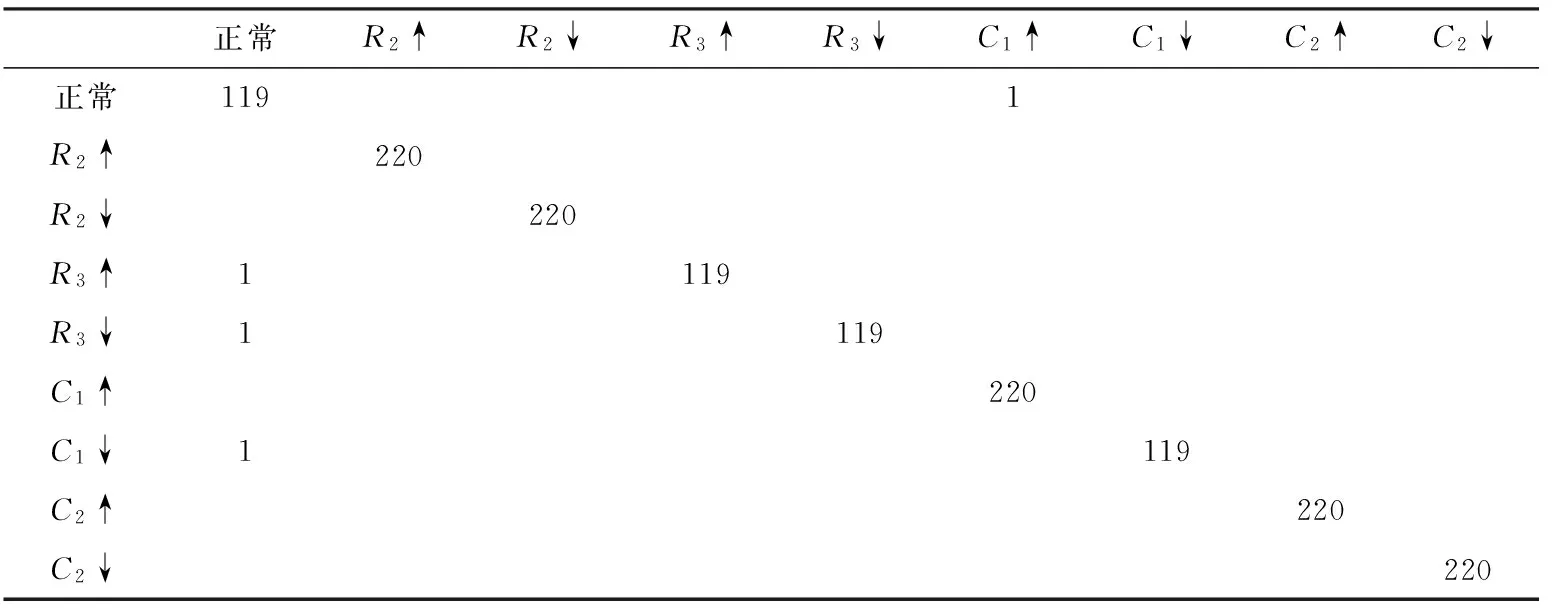
P=(u1,u2,…,up),p

(4)

(5)建立故障向量。根据公式T=XP计算新的训练样本集和测试样本集，从而消除了电路故障原始数据属性之间的相关性，达到降维的目的。因此，通过PCA处理减少了计算量，也可大幅提高系统的学习效率。

2 基于ELM的故障检测

ELM模型只需对输入权和隐藏层偏置进行随机赋值，设置合适的隐藏层结点数，通过最小二乘法得到输出层权值。整个过程一次完成，无需迭代，与BP相比速度显著提高。ELM大幅提高了学习速率，具有良好的泛化能力。

上述N个方程的矩阵形式可写为Hβ=T，其中

E(W)表示期望值和实际值之间的误差平方和，问题求解就是寻找最优的权值W=(a,b,β)使代价函数E(W)最小，其数学模型可表示为

其中，εj=[εj1,εj2,…,εjm]是第j个样本的误差。

通过定理[10]表明：只要隐含层结点数足够多，SLFN就能在输入权随机赋值情况下逼近任何连续函数。但为使SLFN具有良好的泛化性能，通常 。当输入权以随机赋值的方式确定后，所得隐藏层权值可以通过线性方程Hβ=T的最小二乘解解决。

给出一个训练样本N={(xi,ti)|xi∈Rn,ti∈Rm,i=1,…,N}, 激励函数g(x)和隐含层节点数为M。

(1) 随机选取权值ai，偏置bi(i=1,…,M)；

(2) 计算隐层输出矩阵

(3) 计算输出权重β:β=(HTH)HTT。

由此可知，相比于传统的SLFN，ELM在训练的过程中不需要调整输入权值和偏置，只需根据相应算法来调整输出权值β，便可获得一个全局最优解。参数选择较为容易，训练速度显著提升，且不会陷入局部最优。通过ELM进行分类，能达到良好的实时性和准确率[11]。

3 基于PCA和ELM的故障诊断

3.1 诊断方法

基于PCA-ELM的电路故障诊断的过程为：首先向被测电路输入信号源，对电路的输出响应信号进行采样，获取故障信息；然后对采样数据进行PCA预处理，提取故障特征；最后通过ELM分类器进行模式分类确定故障类型，从而实现电路的故障诊断。该方法的结构如图1所示。

图1 故障诊断过程图

3.2 仿真实例

3.2.1 被测电路1--Sallen-key滤波器

本文以Sallen-key滤波器验证算法的有效性。图2是该滤波器电路原理图，图中所示参数值为元件的标称值，各元件容差为电容±5%、电阻±10%；电路激励为正弦信号源。

图2 滤波器电路

(1)样本建立。用Orcad16.3软件对上述电路进行仿真，通过灵敏度分析，发现元器件R2、R3、C1、C2的变化对电路输出响应的影响最大。因此可确定8种故障模式，即R2、R2、R3、R3、C1、C1、C2、C2。其中符号和分别表示偏大和偏小类型的软故障。即

R2,R3：(-50%,-90%)∪[-90%,110%]∪(110%,150%)

C1,C2：(-50%,-95%)∪[-95%,105%]∪(105%,150%)

对电路进行参数分析，可以看出在故障模式下的输出电压波形。图3为R3正常和故障下的输出电压幅频特性。

图3 R3正常和故障下的输出电压幅频特性

从图3中可看出，故障模式下的输出电压频率响应波形与正常模式时相比有较大区别，尤其在1～100 kHz频率范围内，输出电压Vout对应幅值变化最大，最能体现出各个模式下的响应波形的变化差异。因此，可以在1～100 kHz频率范围内选取一组采样点，将其幅值组合成多维形式的特征向量，作为各模式的故障特征，用于训练ELM。本文选取6个采样点的信号幅值作为有效特征值，构成每个故障模式下的特征向量，即频率分别为1 kHz、10 kHz、20 kHz、50 kHz、70 kHz、100 kHz下所对应的输出电压Vout的幅值。针对该带通滤波器电路，如上述8种故障模式，再加上正常模式共9种模式类别，分别对每一模式类别下的电路进行50次蒙特卡诺(Monte-Carlo)分析，其中30种用于训练，另20种用于测试。共得到9×50个输出电压频率响应波形，分别对每一波形按上述方法提取6维的特征向量，构成了故障特征向量组。

(2)样本预处理。利用每次MC分析时输出响应的特征向量，构成训练样本矩阵X1∈R(270，6),测试样本矩阵X2∈R(180，6)。利用X1、X2即可建立主元模型，各特征值及其方差贡献率如表1所示。可见，对于该滤波器，选取前3个主元即可使累计方差贡献率达到99%。

表1 特征值及其贡献率

(3)故障诊断结果。未使用PCA处理后的样本进行分类，得到结果如表2所示。

表2 基于ELM的诊断结果

对经过PCA处理后的新样本进行分类，得到结果准确率为100%，而且耗时较短，两者比较如表3所示。

表3 ELM和PCA+ELM处理结果比较

如表3所示，直接将原始样本数据输入ELM分类器进行分类决策，故障诊断准确率达到98.3%，而经过PCA处理的新样本输入ELM分类器，故障准确率达到100%，而且用时更短。

3.2.2 被测电路2--Elliptic Filter

为进一步验证本文所提方法的有效性，本文用ITC97中的Elliptic Filter进行检测，电路如图4所示。

图4 Elliptic Filter

各元件容差为±5%。对R2、R6、R13、C1、C5设置故障，故障值如表4所示。

表4 器件故障值设置表

设置10种故障，加上正常，共11种状态。方法如上所述，分别对电路每种状态进行50次Monte-Carlo分析，30次用于训练，20次用于测试。其中选取频率为100 Hz，200 Hz，…，1 100 Hz对应下输出电压的值，提取每种波形输出下的11维特征向量。经过PCA处理，变为4维，累计贡献率达到92.04%。最后送入ELM分类器，此时选用隐含层神经数目为280，诊断结果为100%。

表5 Elliptic Filter的诊断结果

由表5所示的诊断结果可以看出，PCA+ELM对10种状态的分类正确率达到了100%，而且整个算法的耗时较短。PCA+ELM对Elliptic Filter电路故障诊断不但能够正确识别出故障的类别，也能满足工程应用中对实时性的要求。

4 结束语

本文对基于PCA和极限学习机的模拟电路故障诊断进行研究，利用PCA对数据样本进行预处理，达到降维的目的，又因ELM用时短，泛化性能好，再通过ELM进行分类，能实现良好的诊断效果。通过对Sallen-key滤波器及Elliptical Filter电路的故障诊断表明，此方法用时短、准确率高，能够实现电路故障的快速检测与准确定位，具有速度快、精度高、鲁棒性好等特点，为故障诊断提供了参考。

[1] 杨士元.模拟系统的故障诊断与可靠性设计[M].北京:清华大学出版社,1993．

[2] 杨士元,胡梅,王红.模拟电路软故障诊断的研究[J].微电子学与计算机,2008,25(1):1-8.

[3] 林美琴,陈艳峰.基于多小波变换的模拟电路故障诊断[J].计算机工程与应用,2009,45(23):239 -241.

[4] Mehran Aminian, Farzan Aminian.A modular fault diagnostic system for analog electronic circuits using neural networks with wavelet transform as a preprocessor[J].IEEE Transactios on Instrument and Measurement,2007,56(3):1546-1554.

[5] 钱莉,姚恒.基于LMD和SVM算法的模拟电路故障诊断[J].电子科技,2015,28(11):82-85．

[6] Wang Cheng,Xie Yongle,Chen Guangju.Fault diagnosis based on radial basis function neural network in analog circuits[C].Tianjin:Chinese Conference on Control and Decision,CCDC,2008.

[7] Toczek W,Kowalewski M.A neural network based system for soft faults diagnosis in electronic circuits[J].Metrology and Measurements Systems,2005,6(4):463-474.

[8] 孙永奎,陈光踽,李辉.灵敏度分析和SVM诊断模拟电路故障的方法[J].电子科学技术学报,2009,38(6):971-974.

[9] 唐静远,师奕兵.采用模糊支持向量机的模拟电路故障诊断新方法[J].电子测量与仪器学报,2009,23(6):7- 12.

[10] 张洪波,何怡刚,周炎涛,等.主成分分析法与概率神经网络在模拟电路故障诊断中的应用[J].计算机测量与控制,2008,16(12):1789-1791.

[11] Huang G B, Zhu Q Y, Siew C K.Extreme learning machine:theory and applications[J]. Neurocomputing,2006,70(1-3):489-501.

[12] 程松,闫建伟,赵登福,等.短期负荷预测的集成改进极端学习机方法[J].西安交通大学学报,2009,43(2):106-110．

[13] 邓万宇,郑庆华,陈琳,等.神经网络极速学习方法研究[J].计算机学报,2010,33(2):279-287．

[14] 潘孝礼,肖东,常玉清,等.基于极限学习机的软测量建模方法研究[J].计量学报,2009,30(4):324-327.

A Fault Diagnosis Method in Analog Circuits Based on PCA-ELM

ZHOU Jiangman

(Wuhan Fiberhome Fuhua Electric Co. Ltd, Wuhan 43000, China)

Based on principal component analysis (PCA) and the extreme learning machine (ELM), a method of fault diagnosis in analog circuits is proposed. The response feature parameters are preprocessed by PCA to generate the major ones. Feature vectors under certain states can be classified using ELM, and fault diagnosis is realized. The ELM enjoys quick learning speed and good generalization performance and compressing data characteristics of PCA. Simulation results on benchmark circuits show that this scheme is feasible with a fault diagnosis accuracy of over 98.3%.

fault diagnosis; analog circuits; extreme learning machine; principal component analysis

2016- 06- 22

周江嫚 (1987-)，女，硕士。研究方向：电路与系统故障诊断等。

10.16180/j.cnki.issn1007-7820.2017.05.020

TN431.1；TP277

A

1007-7820(2017)05-072-05