读懂计算教学的价值所在

【摘要】运算能力是数学能力的核心要素，是数学学科独有的能力。在数学计算教学中，教师应突出学习计算的价值，帮助学生理解运算的算理，寻求合理简洁的运算途径解决问题。

【关键词】数学计算教学；运算能力；价值

【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009（2017）25-0074-02

【作者简介】荆亚琴，江苏省常州市新北区龙虎塘实验小学（江苏常州，213000）教师，一级教师，常州市数学学科带头人。

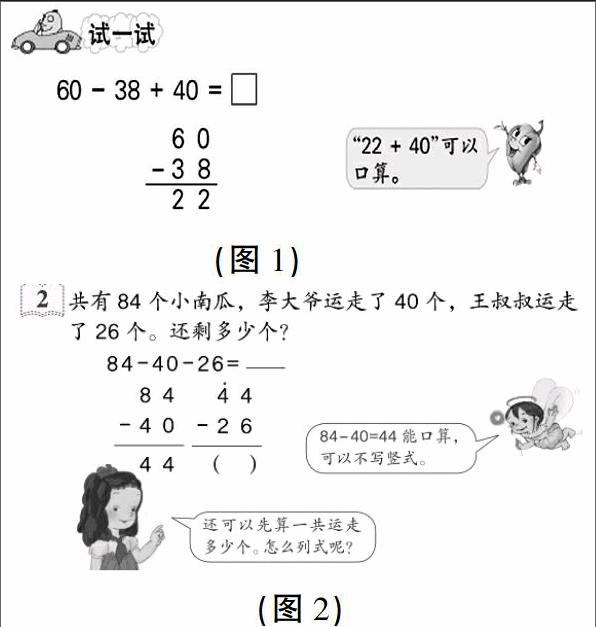
近日，笔者所在年级的同事在备课苏教版二上第5页“试一试：60-38+40”时出现了不同意见，原因是教材中提到“22+40”可以口算（如图1），有的教师认为学生刚接触连加连减竖式，还没有掌握好就要改变计算方法，很可能掌握不牢，提倡22+40也列竖式计算，提高正确率。也有的教师认为就应该按照教材的要求，22+40能口算的，就口算。那么这道算式该如何教？如何处理笔算与口算之间的关系呢？

“数与运算”是小学数学教材中的重要内容，其对象是自然数、分数和小数，包括数的认识与数的运算。我国传统的数学教学强调的是数运算的快速性与准确性，在新课标实施以前，教学大纲对学生运算能力的要求是：“正确、迅速、合理、灵活”，尤其以准确率和速度作为衡量运算能力的标准。正因此，说到运算，很多教师立刻想到“熟能生巧”，认为数学运算能力无非就是依靠多练习，练速度，练正确率。

新课改以来，与运算能力密切相关的数感、符号感进入数学教育的视野，《义务教育数学课程标准（2011版）》明确提出把“运算能力”作为十大核心词之一。运算能力主要是“能够根据法则和运算律正确地进行运算的能力，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。”能够按照一定的程序进行运算只能称之为运算技能；“运算能力”不仅是数学操作技能，还包括观察、记忆、思维、联想等有关的从低级到高级的综合能力，是一种数学思维能力。

笔者查阅了其他相关版本的教材，发现苏教版和人教版（如图2）在教学连加、连减和加减混合的笔算时，都不约而同提到了“能口算的可以不写竖式”。

苏教版和人教版都将100以内的连加、连减和加减混合的计算教学，安排在了小学二年级上学期进行。首先：教材将笔算教学与解决问题的教学有机结合，先从现实情境中提出要解决的计算问题，突出学习计算的价值。不论是苏教版中的“38+42+33”，还是人教版中的“28+34+32”，让学生明确连加、连减或加减混合运算的一般方法是按照同级运算从左往右，依次计算。此外，不论是苏教版的试一试，还是人教版的例2，都努力帮助学生在挖掘信息的基础上，选择解决问题的最佳运算方法，如能口算的就不写竖式，从而使运算过程更简单；这恰恰是在帮助学生养成根据参与运算的數据特点灵活选择算法的自觉意识，能口算的应该大胆口算。该内容的教学，指向的是对数的认识与数的运算的“理解”，而不是指向快速准确计算的目标。“理解”强调的是对数之间关系的认识，是对算理的把握，而快速计算侧重的是对算法的熟悉乃至自动化操作，二者有着截然不同的价值取向。因此，将合理选择算法渗透到笔算教学中，不仅有利于突出运算思维的推理成分，更有利于提升学生的运算策略水平。

事实上，平时的数学教学，教师为了追求口算的速度和笔算的正确率，往往习惯将口算与笔算“割裂”教学。正因如此，教学到二年级《加减混合》这一内容时，即使意识到要让学生掌握灵活的计算方法，但为了追求计算的准确性，教师认为还是选择竖式计算更为稳妥。其实，笔算仅仅是记录计算过程与结果的书面形式，一味地强调竖式笔算，虽然能较快实现技能目标，却也容易造成学生算法认知上的缺陷，以及由此带来的运算程序僵化。再如看到“灵活运算”，教师往往把灵活运算等同于简便计算。传统的简便运算局限于根据运算定律、运算性质将算式变形，这与问题解决策略多样化和寻求合理简洁的运算途径解决问题，还存在较大差距。灵活运算不仅涵盖简便计算的任何一道题，更要让学生在解决问题的过程中运算简便。

这不禁让笔者联想到一次对全校五年级学生调研时的运算题“3.07-0.19×2-1.62”，大约有36%的学生采用以下的方法进行计算。

从追求运算的正确性来说，该题答案正确，学生按照两级运算规则来答题，先算乘除，再算加减。再细细思考，学生在简化运算能力方面却暴露了薄弱之处。简化运算能力，是学生解决问题过程中的优化手段，是在正确合理的方法指导下，使运算过程变得更简洁。如果教师在运算教学中一味追求运算结果的正确率，偏重准确的结果，必然会对题目缺少深入的理解与思考，难以选择解决问题的最佳运算方法，从而会将学生的思维禁锢在机械模仿和记忆的初级水平上。

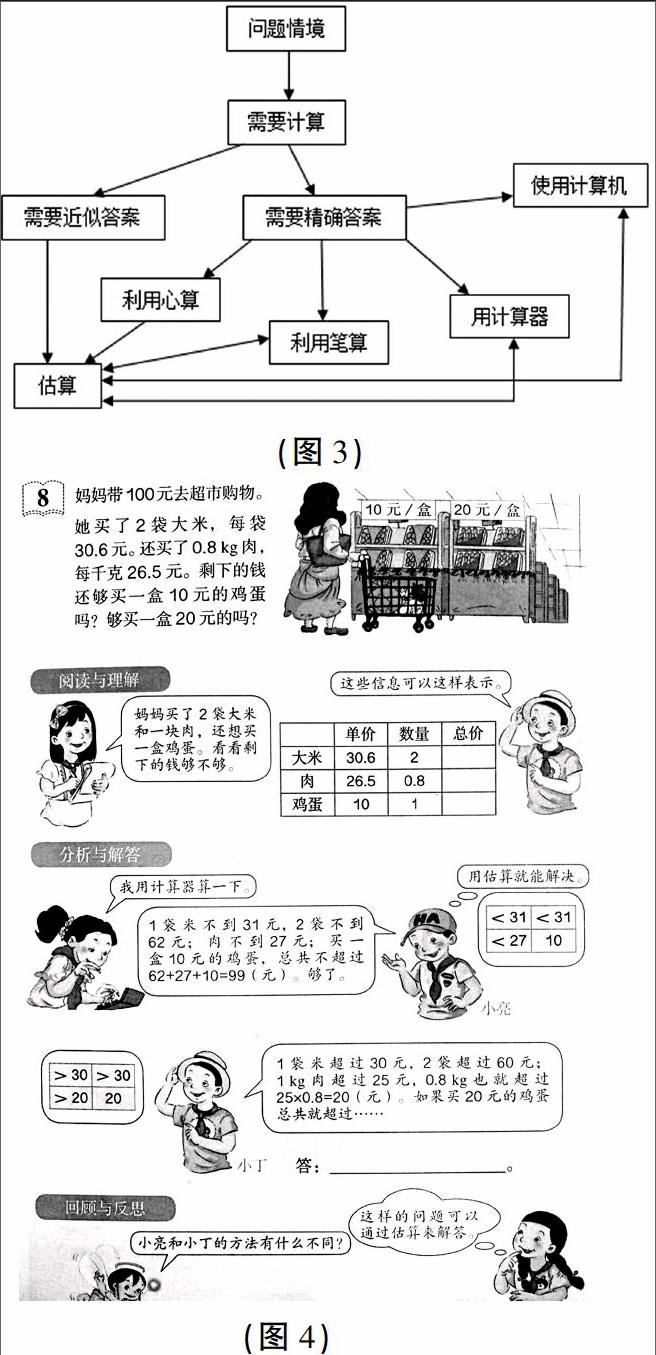
关于运算，美国数学教师学会在1989年编写的《学校数学课程与评价标准》中有一段论述（如图3），反映了其对运算基本概念的理解。当面临实际问题进行计算时，首先应当考虑需要近似答案还是精确答案：如果一个近似答案就足够了，那就估算；如果需要精确答案，那就要依次选择口算、笔算，是否需要使用计算器算等。也就是说，选择计算方法，应在确定了计算方式之后进行。

人教版五上的一道例题（如图4）就较好地诠释了面对实际问题时如何选择适合的方法来解决。

随着课程改革的实施与深化，计算已不再作为独立的内容进行教学。教师要把学习计算与解决问题的过程结合起来，凸显计算是解决问题的手段，解决问题是计算的目的。通过计算教学培养数感，包括借助计算器探索规律，发展数与运算的概念，都是为了提升人的数学素养与运算能力。