帧间自适应的压缩感知谱减去噪方法
2017-05-18畅江张雪英李凤莲
畅江++张雪英++李凤莲


摘 要: 针对应用压缩感知理论对含噪语音进行去噪其信噪比低的问题,以及应用谱减法对含噪语音去噪后语音信号仍不清晰的情况,提出帧间自适应的压缩感知谱减去噪方法。同时,由于传统压缩感知理论不能使语音信号在重构时实现帧间自适应的去噪效果,对此缺陷提出一种改进算法,并且将该算法应用到谱减法的去噪过程中。相比于经典的谱减法,实验结果表明,所提算法对含噪语音进行去噪不仅可以提高含噪语音的去噪效果,还可以有效地解决谱减法无法去除背景噪声及音乐噪声的问题。
关键词: 压缩感知; 谱减法; 语音去噪; 正交匹配追踪算法
中图分类号: TN912.3?34 文献标识码: A 文章编号: 1004?373X(2017)09?0014?04
Abstract: Since the noisy speech denoising based on compressed sensing theory has low signal?to?noise ratio, and the spectrum subtraction used to denoise the noisy speech still has poor speech signal, a speech denoising method based on adaptive inter?frame compressed sensing of spectrum subtraction is put forward. The traditional compressed sensing theory can′t realize the adaptive inter?frame denoising effect while reconstructing the speech signal, so an improved algorithm is proposed, and applied to the denoising process of the spectrum subtraction. The experimental results show that, in comparison with the classical spectrum subtraction, the proposed algorithm used to denoise the noisy speech can improve the denoising effect of the noisy speech, and effectively eliminate the background noise and music noise that the spectrum subtraction can′t do.
Keywords: compressed sensing; spectrum subtraction; speech denoising; orthogonal matching pursuit algorithm
0 引 言
目前,有越来越多的研究已证明压缩感知(Compressed Sensing,CS)理论[1]能够使语音信号在较大的压缩比下达到较好的重构效果[2?4]。此外,还有研究指出该理论可以提高语音信号的抗噪性能,例如文献[5]指出,若噪声分布已知时,通过修改压缩感知的约束条件,用基追踪(Basis pursuit,BP)算法就可抑制噪声。文献[6?8]提出可采用自适应基追踪的方法对语音信号进行去噪。虽然CS理论可以被用来进行语音去噪,但对于噪声较强的语音信号,单独使用CS理论无法获得理想的去噪效果,因此要想采用CS理论对语音信号进行去噪,就需要对该理论本身进行改进,或结合其他理论[9]。
本文根据谱减法[10]能简单有效地去除语音信号中多数噪声的优点以及去噪后的语音仍含有大量背景噪声和音乐噪声的缺点,提出帧间自适应的压缩感知谱减(Adaptive Inter?frame Compressed Sensing of Spectrum Subtraction,AICSSS)去噪方法,并将该方法用于含噪语音的去噪处理中,其中CS的重构算法采用正交匹配追蹤(Orthogonal Matching Pursuit,OMP)算法,但OMP算法在重构时必须根据预先估计好的稀疏度进行重构,而实际上,稀疏度通常不可知,对于语音信号而言,语音信号经分帧进行稀疏化处理后,其每一帧的稀疏度都是完全不同的,所以不能用一个固定的稀疏个数对每一帧语音信号进行重构。为此本文进一步提出了一种帧间自适应的OMP算法,并将该算法与谱减法结合对含噪语音进行去噪处理。实验结果表明,本文的方法能有效修正应用谱减法对含噪语音去噪后存在背景噪声和音乐噪声的缺陷,并且还能改进单独使用CS理论对含噪语音信号的处理效果。
1 压缩感知理论模型
2 语音信号的帧间自适应OMP算法
2.1 帧间自适应OMP算法的基本原理
虽然传统的OMP[12?13]算法具有重构效果好,算法复杂度低的优点,但它却无法在稀疏度未知的情况下进行重构。在实际的仿真实验中,语音信号经分帧稀疏化处理以后,不仅稀疏个数是未知的,而且对于每一帧的语音信号来说,其稀疏度都有很大不同。为此,本文对传统的OMP算法进行改进,提出一种帧间自适应的OMP算法。
所谓的帧间自适应就是在应用CS理论重构语音信号时,根据每帧语音信号稀疏度的不同,自动估算出语音信号重构时所需要的稀疏个数从而达到自适应重构语音信号的目的。
帧间自适应OMP算法是在传统OMP算法的基础上去掉预先设定好的稀疏度,并在每次重构信号时采用残差逐步逼近的方法自动终止迭代,而程序的迭代次数即为所需要的稀疏度。
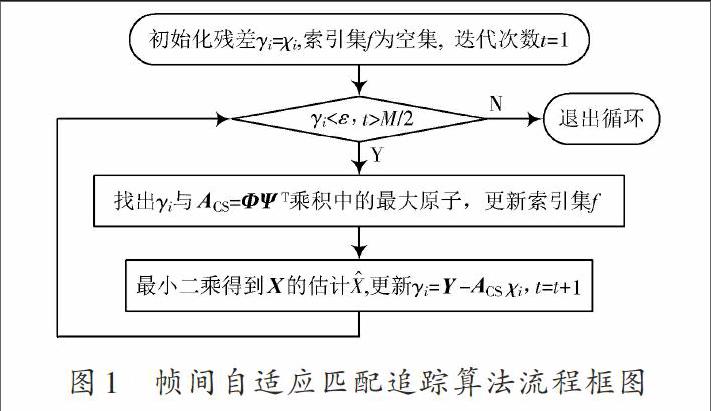
图1为该算法的流程框图,其中,为每次迭代时重构信号的残差,如果残差小于某个设定值则停止迭代,但为了防止迭代过程中残差未能小于某个设定值而出现反复迭代的现象,又设定了一个迭代次数的最大值作为终止条件,这样就完成了语音信号的帧间自适应重构。
2.2 帧间自适应OMP算法的去噪原理
由于语音信号经稀疏化后,其噪声信号的稀疏度非常大,且明显大于其有用信号的稀疏度,为了能使改进后的OMP算法在重构时就达到对语音信号进行去噪的目的,需要分别进行两方面的操作:一是在信号进行稀疏化时,通过设置信号的压缩比,就可先滤除部分噪声;二是在重构语音信号时,需要估算出信号的稀疏个数,若当某一帧的稀疏个数远小于其他帧的稀疏个数时,则可认为该段语音帧为噪声帧,可通过限制其稀疏度阈值的方式将噪声滤除。
通过上述原理就可以滤除语音信号中的部分噪声,经实验发现,在低噪声背景下,采用OMP算法去噪可以得到更高的PESQ值,这说明其主观质量评价要好于经典的谱减法,从实际听觉效果来说它能有效滤除背景噪声,但是对于背景噪声较强的语音噪声,OMP算法去噪重构后的效果并不好。
3 谱减法去噪模型
4 AICSSS去噪方法
由于谱减法计算简单,去噪后的信噪比较高,但主观语音质量评价较低,而CS重建后的语音虽然在强噪声环境下信噪比较低,但其主观质量评价要高于谱减法去噪。基于二者的优缺点,本文提出AICSSS去噪方法。该方法能够有效改善上述两种方法的缺点,提高语音信号的抗噪性能。
原始语音信号经过谱减法去噪后仍然含有大量背景噪声,而这些噪声经变换域变换后得到的稀疏个数要远小于有效信号的稀疏个数,根据这个原理,就可以依据CS理论,调整稀疏度的阈值对语音信号进行去噪。该阈值的选取为实验得出,阈值选取的越大,去噪效果也就越明显,但阈值太大就会影响到所需语音的重构效果,因此在选取阈值方面要根据噪声的强度而定,噪声强度大那么设定的阈值就大,噪声强度小,设定的阈值就小。该方法的具体步骤为:
步骤1:将读入的语音信号进行分帧加窗,采用DCT矩阵对信号进行稀疏化,调节其压缩比,并求出带噪语音的功率谱和噪声功率谱
步骤2:用得到降噪后语音的功率谱开方后即为谱减法初步降噪的语音幅度谱
步骤3:采用高斯随机矩阵对初步降噪的语音幅度谱进行观测,得到观测值同时初始化残差索引集为空集,迭代次数设置迭代终止条件
步骤4:找出残差和感知矩阵乘积中最大值所对应的位置;根据噪声强度,设置稀疏度的阈值,并且更新索引集
步骤5:通过最小二乘法得到的系数逼近并求出每帧信号的稀疏度,把稀疏度大于的信号帧置零,同时更新残差和迭代次数
步骤6:判断是否满足若满足则停止迭代,不满足则跳至步骤(4)。
5 实验的仿真结果及分析
本文采用信噪比SNR和PESQ值的方法评估去噪后的语音质量,其中压缩比和信噪比SNR的公式为:
实验的测试软件为Matlab,对象为10个男生和10个女生的语音。由于实际的噪声经白化及同态滤波处理后,都可以转化为高斯白噪声,所以本文采用Noisex92数据库中的高斯白噪声作为噪声语音。
实验1:取512个样点为语音信号的帧长,当含噪语音的信噪比为0 dB,5 dB,10 dB,15 dB,20 dB时,分别考察谱减法、帧间自适应OMP算法以及AICSSS去噪方法的去噪效果,得到的实验结果如表1所示,在本实验中,除谱减法外,剩下两种算法的压缩比统一设定为0.3。
由表1可知,虽然谱减法的信噪比都优于帧间自适应OMP算法的信噪比,然而对于语音质量而言,当原始语音的信噪比大于15 dB时,即使谱减法的信噪比好于帧间自适应OMP算法的信噪比,帧间自适应OMP算法的主观语音质量PESQ值都要好于谱减法。基于这个原因,本文提出AICSSS方法就可以有效改善它们的缺陷,从表1最后一列可以看出AICSSS方法不论是从信噪比方面还是从PESQ值上效果都有所提高,在20 dB时,AICSSS方法在信噪比方面提高不大,这是因为原始语音信号进行去噪以后语音的噪声强度低,所以对含噪语音信号去噪后的信噪比改善不明顯。
图2为上述三种方法在信噪比为5 dB时的效果图,其中语音信号的压缩比仍然为0.3,从图中可以看出,AICSSS去噪后的效果明显好于其他两种方法,在实际的主观听音测试时,语音信号的背景噪声大大减小,并且无不连续的声音状态存在。
实验2:在与实验1相同的条件下,设置原始语音噪声的信噪比为10 dB,改变压缩比分析AICSSS算法的实验结果。当原始语音的信噪比固定为10 dB时,由于单独使用谱减法时不会考虑压缩比的变化,所以,这时单独使用谱减法的信噪比恒为16.688,PESQ值恒为1.633。
从表2可以看出,在原始语音的信噪比为10 dB的情况下,本文算法在压缩比为0.4时的效果最好,PESQ值最高,在压缩比沿着0.4增大或减小时,语音质量都会逐步下降,这是因为当增大时,含噪语音的一部分噪声信号也被重构出来。可见在压缩比不同时,AICSSS方法的去噪效果也会有所变化。
6 结 论
本文进一步证明了压缩感知理论在语音信号去噪领域中的可行性,基于经典的谱减法和压缩感知的去噪重构方法的不同优缺点,本文提出一种帧间自适应的压缩感知谱减去噪方法,该方法不仅克服了谱减法具有背景噪声和音乐噪声的缺点,同时也相对的改善了压缩感知理论在较大背景噪声下重构效果不理想的情况。另外,本文还比较了在不同压缩比的情况下本文算法的实验效果,实验结果表明,在相同的背景噪声下,信号重构时压缩比不同会对语音信号的去噪效果有直接影响。关于压缩感知理论在含噪语音中的应用还有待进一步的研究。
参考文献
[1] DONOHO D. Compressive sampling [J]. IEEE transactions on information theory, 2006, 52(4): 1289?1306.
[2] LOW S Y, PHAM D S, VENKATESH S. Compressive speech enhancement [J]. Speech communication, 2013, 55(6): 757?768.
[3] DONOHO D L, ELAD M, TEMLYAKOV V N. Stable recovery of sparse overcomplete representations in the presence of noise [J]. IEEE transactions on information theory, 2006, 52(1): 6?18.
[4] SHARMA P, ABROL V, SAO A K. Compressed sensing for unit selection based speech synthesis [C]// Proceedings of 2015 23rd European Signal Processing Conference. [S.l.]: IEEE, 2015: 1731?1735.
[5] TSAIG Y, DONOHO D L. Extension of compressed sensing [J]. Signal processing, 2006, 86(3): 549?571.
[6] 孙林慧,杨震.基于自适应基追踪去噪的含噪语音压缩感知[J].南京邮电大学学报(自然科学版),2011,31(5):1?6.
[7] 程经士.压缩感知理论在语音信号去噪中的应用[J].现代电子技术,2012,35(7):84?85.
[8] DO T T, LU G, NAM N, et al. Sparsity adaptive mating pursuit algorithm for practical compressed sensing [C]// Proceedings of 2008 42nd Asilomar Conference on Signals, Systems and Computers. Pacific Grove: IEEE, 2008: 581?587.
[9] 李凤莲,畅江,张雪英,等.基于压缩感知的语音盲稀疏重构算法及其去噪应用[J].中南大学学报(自然科学版),2015(1):164?170.
[10] PARDEDE H, IWANO K, SHINODA K. Spectral subtraction based on non?extensive statistics for speech recognition [J]. IEICE transactions on information & systems, 2013, 96(8): 1774?1782.
[11] JI Y, YANG Z. Study on adaptive compressed sensing & reconstruction of quantized speech signals [J]. Journal on advances in signal processing, 2012(1): 1?21.
[12] TROPP J, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE transactions on information theory, 2008, 53(12): 4655?4666.
[13] 刘记红,黎湘,徐少坤,等.基于改进正交匹配追踪算法的压缩感知雷达成像方法[J].电子与信息学报,2012,34(6):1344?1350.
[14] YKHLEF F. An efficient solution to improve the spectral noise suppression rules [J]. Digital signal processing, 2013, 23(5): 1578?1584.
[15] 高留洋,朱文,桑振夏,等.一种基于改进的谱减法的语音增强算法[J].现代电子技术,2012,35(7):60?62.
