基于模糊与虚拟力预测的多机器人围捕问题研究

张旭　贾磊磊　李玲

[摘要]多机器人追捕一逃跑问题一直是人工智能研究的一个典型问题。当存在多个机器人时，他们可以通过实时通信和协商来提高追捕效率，即机器人协调合作问题。因此，多机器人围捕问题具有一定的代表性，已成为目前研究多个智能体合作与协调系统的理想研究平台。本文通过对多机器人围捕问题的研究与分析，采用模糊控制的围捕协调策略，成功的完成了围捕任务。

[关键词]多机器人；围捕；模糊控制；协调策略

0引言

近年来，多机器人系统研究因其自身的复杂性和并行性，以及广泛的应用领域，受到越来越多专家和学者的关注。多机器人协调与对抗是多机器人系统研究中的基本问题，而多机器人围捕问题是多机器人系统研究的一个典型问题。随着机器人技术的不断发展。多机器人系统的研究成果已经广泛应用于工业、航天、军事和民用服务业等各个领域。多机器人围捕是指在多机器人追捕过程中，不仅要顺利完成追逃任务，同时在特定的条件下保持一定的追捕队形实现最终的一种“包围”状态Ⅲ。能够有效应用于多机器人围捕问题的协调策略，经过简化后同样能够适用于一般的追捕任务。因此，本文主要针对多机器人围捕问题的协调策略进行分析研究，更加具有典型的意义。

本文主要讨论的多机器人围捕问题是基于局部信息感知的，即在追捕过程中，双方并不能完全感知周围的所有信息。因为在实际应用中，追逃双方往往不能完全探测到周围的复杂地形以及对抗双方的实时位置信息。

1基于虚拟力预测的逃逸机器人策略

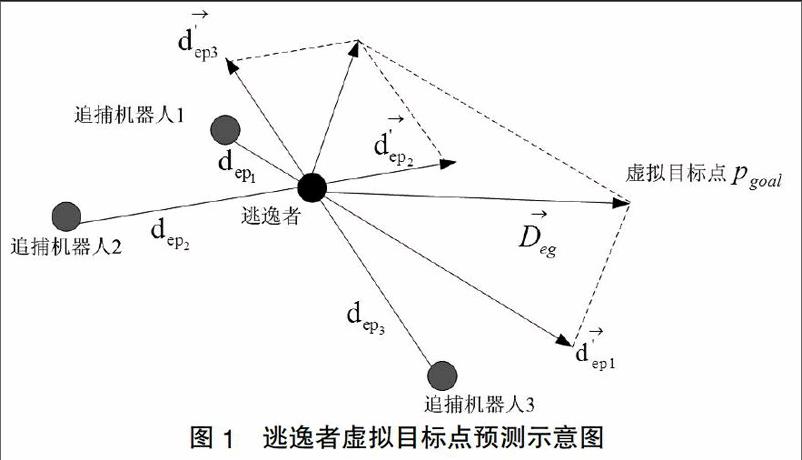
文中主要讨论多机器人围捕单机器人的策略分析问题，对于单个逃逸者而言，在速度固定的情况下，需要躲避所有的追捕者以防止被围捕，因此只需要讨论对抗策略，不涉及自身的协调问题。根据图1分析可知，距离逃逸者最近的追捕者p_k对逃逸者的威胁最大，反之距离越远的追捕者对逃逸者的威胁越小。根据每个追捕者与逃跑者的位置距离的远近，设置反比例权系数，对于逃逸者当前的虚拟目标点预测计算如图1所示。

根据传感器反馈的位置信息，找出距离逃逸者最远的追捕者i，其距离逃逸者的距离设为d_epi，令它对逃逸者的威胁系数设为λ_d，即距离最大的追捕者相对于逃逸者的反矢量距离，则其他追捕者对逃逸者的威胁分别取为（仿真中令λ_d=3）：

（1）

（2）

则求得逃逸者到虚拟目标的矢量为：

（3）

由式（3）结合当前逃逸者的位置可得到逃逸者的虚拟目标点p_goal。若最终无法找到合适的逃逸者的虚拟目标点，即没有可以选择的可行方向，或者逃逸机器人与每个追捕机器人之间的距离均小于某一确定阈值时，则围捕任务结束。

2基于模糊控制的追捕机器人协调策略

模糊集合理论的概念是L.A.Zadeh教授在1965年在Information&Control杂志中首次提出，随后得到了不断的扩展与完善，逐渐由数学领域应用推广到工业及信息等领域的应用。模糊逻辑控制就是在模糊集合的应用与发展中提出的一个新的分析方法及控制策略。

在本文中。假设一共有三个围捕机器人。通过模糊逻辑进行分析，对每一个追捕机器人的每一步运动方向及夹角进行控制，通过实时在线检测。每一步确定距离逃逸者最近的追捕机器人为p_k，距离最近的追捕机器人在追捕过程中直接奔向逃跑者的下一步的虚拟目标点。此时对于追捕机器人p_k而言，其每一步的追捕效率是最高的。对于其它两个距离逃逸者较远的追捕机器人，采用模糊逻辑控制，来确定其每一步的运动方向。即对于除p_k以外的两个追捕机器人，输入为每一个追捕机器人与p_k的夹角大小，输出为追捕机器人的追捕运动的方向角。以逃跑机器人为中心，实时检测任意一个追捕机器人与p_k的夹角大小θ₁（θ₁是指追捕机器人与p。之间较小的小于180～的夹角）。将θ₁量化为三个论域（0°，90°），（60°，120°），（90°，180°），并按照一定的隶属度关系使论域与模糊变量{小（s），中（M），大（L）}湘对应。

进一步的，通过解模糊来确定两个追捕机器人每一步的运动方向及夹角θ₂。将θ₂量化為三个论域：（扩大与p_k夹角即反向旋转60°），（不旋转即保持原有运动方向）和（缩小与p_k夹角即正向旋转60°），并按照一定的隶属度关系使该论域与模糊变量的三个语言取值{F，Z，N}相对应。

三个追捕者最终的运动状态为追上逃跑者，同时呈120°夹角包围逃跑者的状态，此时追捕任务结束。

模糊控制规则如下：

规则1：if θ₁ is S then θ₂ is F；

规则2：if θ₁ is M then θ₂ is Z；

规则3：if θ₁ is L then θ₂ is N……

3确定障碍物环境中机器人运动方向

本文仿真环境为mobotsim软件，该软件包含传感器信息，可以自由定义传感器个数。本文在分析研究过程中，选择传感器的个数为三个，设定传感器的有效范围为三米。当传感器的当前测量返回值为3时，说明此传感器探测到障碍物的距离为3m或当前状态下障碍物相距相对较远没有探测到障碍物，因此默认3m以外的障碍物对机器人的影响忽略不计。

根据当前追捕机器人与逃逸机器人分别的传感器输入测量值的大小，按照一定的比例，对避障行为与追逃双方根据围捕策略确定的运动方向进行矢量和计算，最后确定各个追逃机器人的每一步的最终运动方向，

根据“木桶原理”，对于任意一个机器人的三个传感器输入值，找出其最小值设为λ_min，λ_min∈（0，3m）。根据λ_min值的大小，进而分别确定围捕任务时目标策略与避障策略的权系数ω₁和ω₂，其中ω₁+ω₂=1。当λ_min∈（0，1）时，ω₁取值为0.2，ω₂取值为0.8；当λ_min∈[1，2]时，ω₁取值为0.4，ω₂取值为0.6；当λ_min∈（2，3）时，ω₁取值为0.8，ω₂取值为0.2。设任意时刻机器人根据目标选择运动方向的转角为θ_F，避障策略的转角为θ_Z，则机器人每一步最终的运动方向角θ为：

θ=ω₁θ_F-ω₂θ_Z （4）

4设置追捕者优先级

在围捕过程中，若追捕机器人追捕速度远大于逃逸者的速度，或者多个机器人运动到障碍物较复杂且距离较近区域时，根据当前的策略选择运动方向后，由于追捕机器人之间的互相影响，可能会导致两个追捕者停滞运动而导致最终的围捕失败的结果。由于传感器的感应范围限制在0到3m之间，因此当机器人的运动速度过大时，可能会造成双方位置距离较小的状态，或是此时若两边存在类似对称的障碍物，则可能陷入局部极小永远无法继续运动。而且，当机器人的速度过大时，对仿真的有效性验证也有影响，且在一定程度上会影响避障和路径选择策略的效果。因此本文在仿真时选择比较接近的追逃机器人速度，即尽量保证追捕者与逃逸者在速度上不存在优劣，以便更加直观有效的对追逃协调策略的性能进行验证。

同时，在多机器人围捕过程中，对追捕机器人分别设置优先级别，设RI>R2>R3（1、2、3为仿真中机器人的编号），即1号追捕机器人优先级最高，3号优先级最小。若是出现了上述可能的陷入局部运动失败的情况，根据优先級判断，优先级别高的机器人根据当前策略继续前进，优先级别较低的机器人稍作停顿，等待下一周期策略选择后再继续运动，这样就能够在不影响策略整体效果的情况下及时的转化僵局保证围捕任务的顺利进行。

5仿真实验

本文的仿真环境为mobotsim移动机器人仿真软件，仿真环境为用网格表示的二维坐标平面，其中一个单位网格表示实际lm的距离。除初始位置不同外，各个机器人的其它性能参数均相同，即追捕机器人与逃逸机器人分别具有相同的传感器探测范围，大小体积相等。

基于模糊控制的多机器人围捕仿真结果如图3所示。由图可知，仿真结果达到了良好的协调围捕效果，同时验证了本文中所研究围捕策略的有效性及稳定性。

[责任编辑：杨玉洁]