一类二阶微分方程新的Kamenev型振动准则
2017-05-18杨甲山覃桂茳
杨甲山, 覃桂茳
(1.梧州学院 信息与电子工程学院,广西 梧州 543002; 2.梧州学院 复杂系统仿真与智能计算实验室,广西 梧州 543002)
一类二阶微分方程新的Kamenev型振动准则
杨甲山1,2, 覃桂茳1,2
(1.梧州学院 信息与电子工程学院,广西 梧州 543002; 2.梧州学院 复杂系统仿真与智能计算实验室,广西 梧州 543002)
研究了一类具有非线性中立项的二阶变时滞微分方程的振动性.采用广义的Riccati变换及多种不等式技巧,获得了该类方程的2个新的Kamenev型振动准则,这些准则能用于其他已知结果不适用的情形,推广并改进了相关文献的结果.
振动性;变时滞;非线性中立项
Journal of Zhejiang University(Science Edition), 2017,44(3):274-280
0 引 言
在微分方程定性理论的研究中,振动性理论作为重要的研究方向之一,具有极为广泛的应用背景,近年来引起了国内外众多学者的极大兴趣和高度关注,该研究领域取得了大量成果[1-22].笔者考虑如下一类形式非常广泛的具有非线性中立项的二阶Emden-Fowler型微分方程:
{a(t)|[x(t)+p(t)xα(τ(t))]′|β-1[x(t)+p(t)xα(τ(t))]′}′+
q(t)|x(δ(t))|γ-1x(δ(t))=0,t≥t0
(1)
的振动性.为了叙述方便,假设:
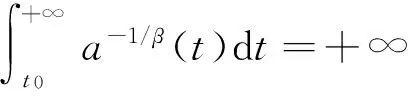

关于方程(1)的解及其振动性的定义可参见文献[1]或[9].对具有非线性中立项的微分方程振动性的研究是一项很困难的工作,因此学者们或是回避这类方程,或是通过附加一些条件将其转化为线性中立项进行讨论[1-4,6-17].仅有文献[5]直接研究具有一个拟线性中立项的一阶微分方程:
[x(t)-pxα(t-τ)]′+
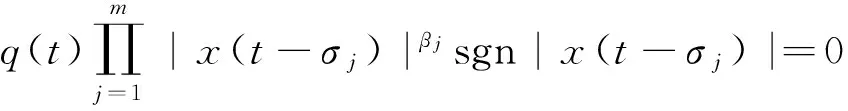
得到了其解振动的一些判别准则.
最近,文献[15]研究了方程(1)的特殊情形(即当α=1时,相当于中立项是线性的情形)的振动性,得到了如下结果:
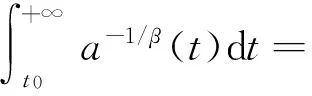
则方程
{a(t)|z′(t)|β-1z′(t)}′+
q(t)|x(δ(t))|γ-1x(δ(t))=0(t≥t0)
(2)
是振动的,其中函数Q(t)=q(t)[1-p(δ(t))]γ,z(t)=x(t)+p(t)x(τ(t)),k>0为常数.
定理A是文献[15]中的定理2.2,也是其主要结果.值得注意的是,当β<γ时,文献[15]没有得到方程(2)的振动准则,且其条件“a′(t)≥0”似乎较为苛刻.受以上研究的启发,笔者利用Riccati变换技术和多种不等式(如Bernoulli不等式、Yang不等式和Hölder不等式等)技巧来研究具有非线性中立项的微分方程(1)的振动性,得到了该方程振动的Kamenev型振动准则,而作为方程(1)的特殊情形,即当α=β=γ=1或者α=1且β=γ时的情形,本文的这些振动准则改进了现有文献中的一系列结果.
1 方程振动的判别定理
首先给出4个引理,其中引理1由函数f(x)=xλ(0<λ≤1)的凹凸性便可证得,引理2~4为公知的不等式,略去其证明.
引理1 设X,Y为非负实数,则当0<λ≤1时,Xλ+Yλ≤21-λ(X+Y)λ.
引理2(Bernoulli不等式) 对任意实数x>-1,当0≤r≤1时,(1+x)r≤1+rx,当r≤0或r≥1时,(1+x)r≥1+rx.
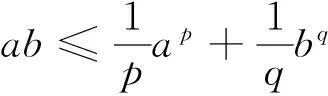
方便起见,引入下列记号:
z(t)=x(t)+p(t)xα(τ(t)),
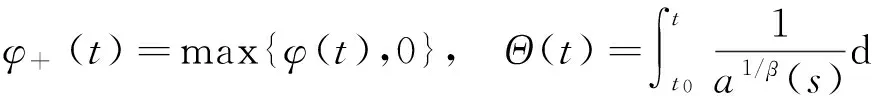
定理1 设(H1)和(H2)成立,若存在函数φ∈C1([t0,+∞),(0,+∞))及常数ω≥0,使得
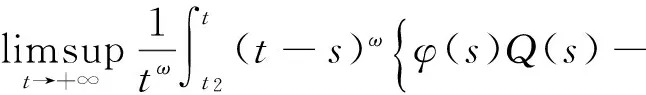
(3)
其中函数
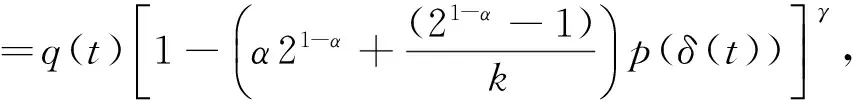
(4)
而t2≥t0,k>0和m>0均为常数,则方程(1)是振动的.
证明 反证法:设方程(1)存在一个非振动解x(t),不失一般性,设x(t)最终为正(当x(t)最终为负时类似可证),则∃t1≥t0,使得当t≥t1时,x(t)>0,x(τ(t))>0,x(δ(t))>0.由方程(1),并注意到函数z(t)的定义,可得z(t)≥x(t)>0(t≥t1),且[a(t)|z′(t)|β-1z′(t)]′=-q(t)xγ(δ(t))<0,
(5)
利用条件(H1),由式(5)易得z′(t)>0(t≥t1).分别利用引理1及引理2,可得
x(t)=z(t)-p(t)xα(τ(t))=z(t)-p(t)[1+xα(τ(t))]+p(t)≥z(t)-21-αp(t)[1+x(τ(t))]α+p(t)≥z(t)-21-αp(t)[1+αx(τ(t))]+p(t)=z(t)-α21-αp(t)x(τ(t))+(1-21-α)p(t)≥z(t)-α21-αp(t)z(τ(t))+(1-21-α)p(t)≥ [1-α21-αp(t)]z(t)-(21-α-1)p(t).
(6)
定义函数w(t)如下:
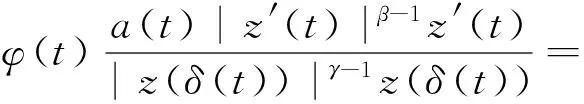
(7)
则有w(t)>0(t≥t1).利用式(5),(6)及a(t)(z′(t))β≤a(δ(t))(z′(δ(t)))β,由式(7)可推得

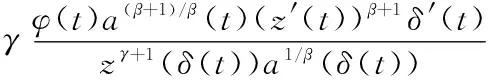
(8)
注意到z(t)>0,z′(t)>0(t≥t1),因此
z(δ(t))≥z(δ(t1))=k(t≥t1).
(9)
其中常数k>0.于是,利用式(7)、(9)和函数Q(t)的定义,由式(8),可得
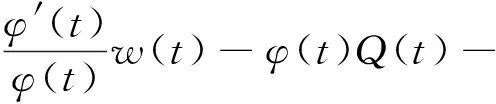
(10)
(i) 若β=γ,则z(γ-β)/β(δ(t))=1.
(ii) 若β<γ,则由式(9)知,z(γ-β)/β(δ(t))≥k(γ-β)/β.

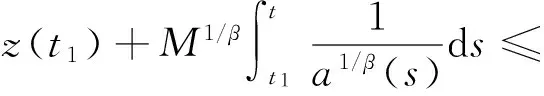
因此存在常数m>0,使得当t2≥t1充分大时,有
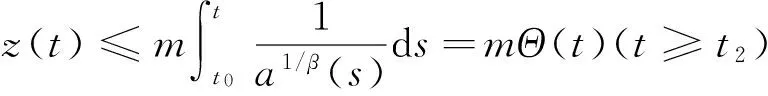
于是
z(γ-β)/β(δ(t))≥[mΘ(δ(t))](γ-β)/β.
(11)
现将式(11)中的t改成s,两边同乘以(t-s)ω,再从t2到t(t≥t2)积分,得


(12)

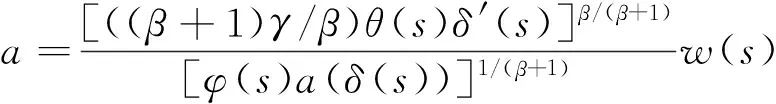
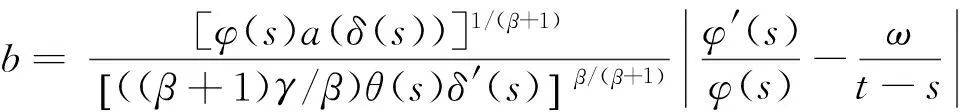
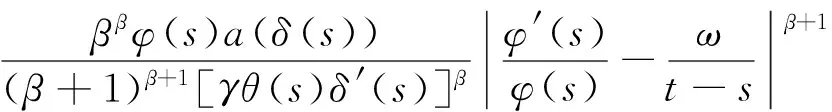
代入式(12),得
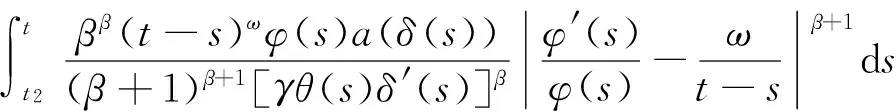

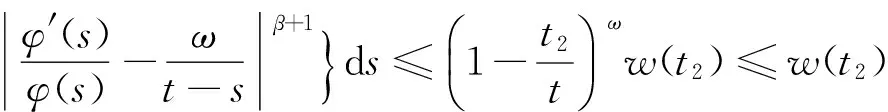
(13)
与式(4)矛盾.定理证毕.
推论1 设(H1)和(H2)成立,若存在函数φ∈C1([t0,+∞),(0,+∞)),使得
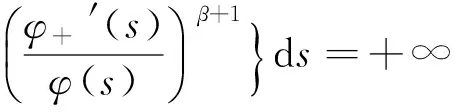
其中常数t2,k,m及函数Q(t)和θ(t)的定义都同定理1,则方程(1)是振动的.
证明 在定理1中,取ω=0,即可得推论1成立.

+∞,
则方程
[a(t)|x′(t)|β-1x′(t)]′+
q(t)|x(δ(t))|β-1x(δ(t))=0(t≥t0)
(14)
是振动的.
证明 在方程(1)中,令p(t)≡0且β=γ,并在推论1中取φ(t)=Θβ(δ(t)),即可得推论2.
注1 当α=1(即中立项是线性的情形)且β≥γ时,由推论1可得定理A(即文献[15]中的定理2.2),但这里去掉了文献[15]中的限制条件“a′(t)≥0”,且当β≤γ时也满足方程(1)的振动准则;而推论2就是SUN等[16]得到的关于方程(14)振动的主要判别定理.
若定理1中的条件(3)不成立,则方程(1)的振动准则如下:
定理2 设(H1)和(H2)成立,若存在函数φ(t)∈C1([t0,+∞),(0,+∞))及ξ1(t),ξ2(t)∈L2([t0,+∞),R),使得对∀u≥t2,有
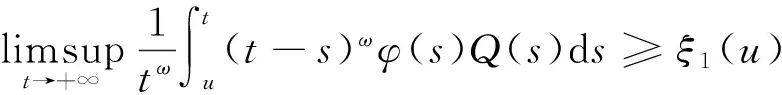
(15)
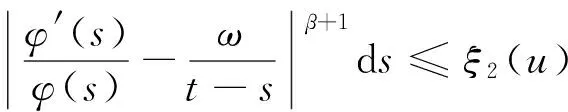
(16)
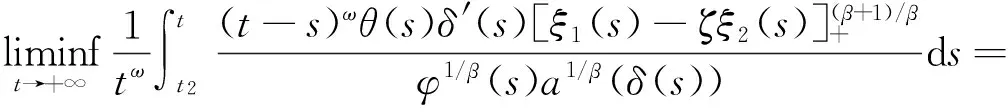
+∞,
(17)
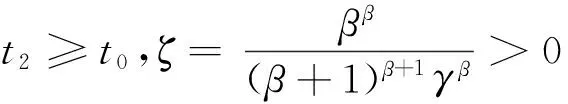
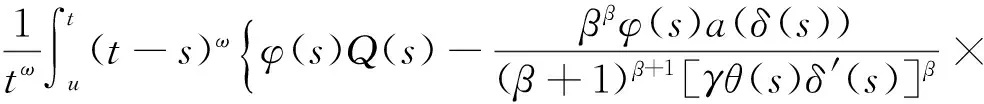

便可得
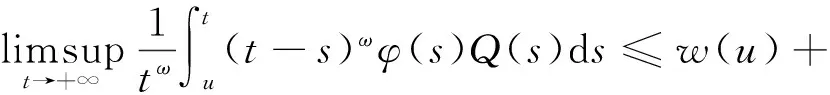
利用式(15)和(16),即可得

ξ1(u)-ζξ2(u)≤w(u),u≥t2≥t0.
(18)

注意到式(15),有
w(t2)-ξ1(t2)≤M0,
(19)
其中M0是常数.这样,根据式(19)就可断言:
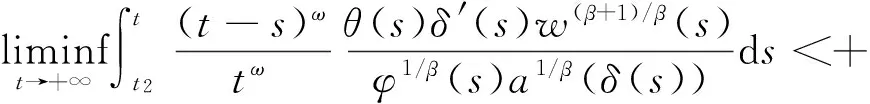
(20)
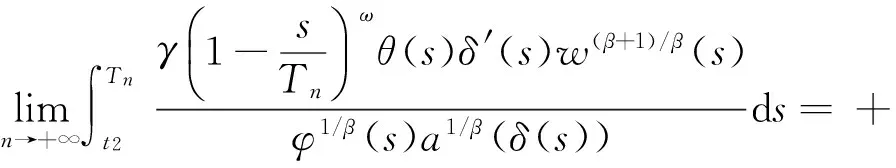
(21)
(22)
则对充分大的正整数n,有
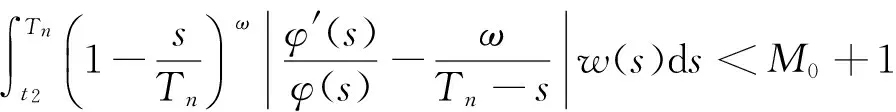

(23)
另一方面,应用引理4中的Hölder不等式,得

(24)
但由式(16)知,上式右边是有界的,这与式(22)矛盾! 式(20)得证.
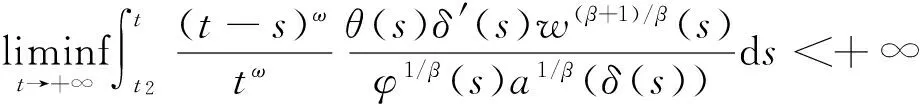
这与式(17)矛盾! 定理证毕.
推论3 设(H1)和(H2)成立,若存在函数φ(t)∈C1([t0,+∞),(0,+∞))及ξ1(t),ξ2(t)∈L2([t0,+∞),R),使得对∀u≥t2,有

(25)
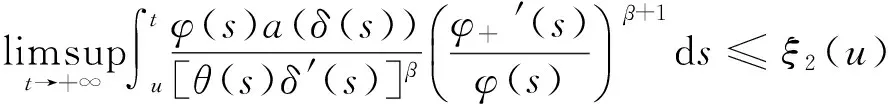
(26)
且ξ1和ξ2满足

(27)
其中常数t2,ζ及函数[ξ1(s)-ζξ2(s)]+,Q(t)和θ(t)的定义均同定理2,则方程(1)是振动的.
例1 考虑二阶时滞微分方程:

(28)
其中常数q0>0.这相当于方程(1)中a(t)≡1,p(t)=1/5,q(t)=q0/t2,τ(t)=t/5,δ(t)=t,α=1,β=1,γ=1.容易验证条件(H1)与(H2)均满足.现取φ(t)=t,则当q0>5/16=0.312 5时,
因此,由推论1知,当q0>0.312 5时方程(28)是振动的.
注2 现用文献[7]中的定理3.4来判定方程(28)的振动性:因为当q0>2.5时,

所以当q0>2.5时方程(28)是振动的.这说明本文定理的特殊情形即当α=1(相当于方程(1)的中立项是线性的)时的振动准则要比文献[7]的有关结论“精细”得多.
例2 考虑具非线性中立项的二阶微分方程
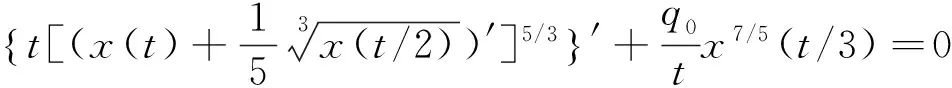
t≥1,
(29)
其中常数q0>0.这相当于方程(1)中α=1/3,β=5/3,γ=7/5,a(t)=t,p(t)=1/5,q(t)=q0/t,τ(t)=t/2,δ(t)=t/3.显然条件(H1)和(H2)均满足.现取φ(t)=1,由于β>γ,且
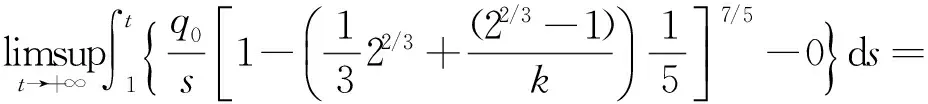
+∞,
所以由推论1知,方程(29)是振动的.
注3 由于方程(29)是具有非线性中立项的微分方程,并且β≠γ,所以文献[1-4,6-17,19-22]中的定理均不能用于方程(29).
从以上例子可看出,即使中立项是线性的,即当α=1且β=γ时,本文的振动准则也是较“精准”的,几乎是方程(1)振动的“sharp”条件,所以本文定理推广、改进并丰富了现有文献的结果.
[1]AGARWALRP,BOHNERM,LIWT. Nonoscillation and Oscillation: Theory for Functional Differential Equations[M]. New York: Marcel Dekker,2004.
[2] HASANBULLI M, ROGOVCHENKO Y V. Oscillation criteria for second order nonlinear neutral differential equations[J]. Appl Math Comput,2010,215:4392-4399.
[3] LI T, AGARWAL R P, BOHNER M. Some oscillation results for second-order neutral differential equations[J]. J Indian Math Soc,2012,79:97-106.
[4] LI T, ROGOVCHENKO Y V, ZHANG C. Oscillation of second-order neutral differential equations[J]. Funkc Ekvac,2013,56:111-120.
[5] LIN X,TANG X.Oscillation of solutions of neutral differential equations with a superlinear neutral term[J]. Appl Math Lett,2007,20:1016-1022.
[6] HAN Z, LI T, SUN S, et al. Remarks on the paper [Appl Math Comput 207 (2009) 388-396][J]. Appl Math Comput,2010,215:3998-4007.
[7] SUN S R, LI T X, HAN Z L, et al. Oscillation theorems for second-order quasilinear neutral functional differential equations[J]. Abstract and Applied Analysis,2012,2012(1085-3375):933-947.
[8] YANG J S, QIN X W. Oscillation criteria for certain second-order Emden-Fowler delay functional dynamic equations with damping on time scales[J].Advances in Difference Equations,2015,2015(1):1-16.
[9] 杨甲山.具正负系数和阻尼项的高阶泛函微分方程的振动性[J].华东师范大学学报:自然科学版,2014(6):25-34,38. YANG J S. Oscillation of higher order functional differential equations with positive and negative coefficients and damping term[J]. Journal of East China Normal University: Natural Science,2014(6):25-34,38.
[10] LI T, ROGOVCHENKO Y V. Oscillation theorems for second-order nonlinear neutral delay differential equations[J]. Abstract and Applied Analysis,2014:Article ID 594190.
[11] 杨甲山,方彬.一类二阶中立型微分方程的振动性[J].数学的实践与认识,2013,43(23):193-197. YANG J S, FANG B. Oscillation of a class of second order neutral differential equations[J]. Mathematics in Practice and Theory,2013,43(23):193-197.
[12] 杨甲山.具阻尼项的高阶中立型泛函微分方程的振荡性[J].中山大学学报:自然科学版,2014,53(3):67-72. YANG J S.Oscillation of higher order neutral functional differential equations with damping[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2014,53(3):67-72.
[13] YANG J S, QIN X W, ZHANG X J. Oscillation criteria for certain second-order nonlinear neutral delay dynamic equations with damping on time scales[J]. Mathematica Applicata,2015,28(2):439-448.
[14] 杨甲山,覃学文.具阻尼项的高阶Emden-Fowler型泛函微分方程的振荡性[J].中山大学学报:自然科学版,2015,54(4):63-68. YANG J S, QIN X W. Oscillation of higher hrder Emden-Fowler functional differential equations with damping[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni,2015,54(4):63-68.
[15] 黄记洲,符策红.广义Emden-Fowler方程的振动性[J].应用数学学报,2015,38(6):1126-1135. HUANG J Z, FU C H. Oscillation criteria of generalized Emden-Fowler equations[J].Acta Mathematicae Applicatae Sinica,2015,38(6):1126-1135.
[16] SUN Y G, MENG F W. Note on the paper of Dzurina and Stavroulakis[J]. Appl Math Comput,2006,174:1634-1641.
[17] 杨甲山,方彬.一类二阶中立型微分方程的振动和非振动准则[J].四川师范大学学报:自然科学版,2012,35(6):776-780. YANG J S, FANG B. Oscillation and non-oscillation criteria for a class of second order neutral differential equations[J]. Journal of Sichuan Normal University: Natural Science,2012,35(6):776-780.
[18] 莫协强,张晓建,杨甲山.一类高阶泛函微分方程非振动解的存在性[J].四川师范大学学报:自然科学版,2014,37(6):861-866. MO X Q, ZHANG X J, YANG J S. Existence of nonoscillatory solutions for a class of higher order functional differential equations[J]. Journal of Sichuan Normal University: Natural Science,2014,37(6):861-866.
[19] 杨甲山.具可变时滞的二阶非线性中立型泛函微分方程的振动性[J].浙江大学学报:理学版,2016,43(3):257-263. YANG J S.Oscillation of certain second-order nonlinear neutral functional differential equations with variable delay[J]. Journal of Zhejiang University: Science Edition,2016,43(3):257-263.
[20] 于强,杨甲山.二阶非线性变时滞中立型微分方程的振荡性分析[J].安徽大学学报:自然科学版,2016,40(4):22-29. YU Q, YANG J S. Oscillation analysis of second-order nonlinear variable delay neutral differential equations[J]. Journal of Anhui University:Natural Science Edition,2016,40(4):22-29.
[21] 于强,杨甲山.时间测度链上一类二阶非线性中立型泛函动态方程的振荡性[J].西北师范大学学报:自然科学版,2015,51(5):12-17. YU Q, YANG J S. Oscillation for certain second-order nonlinear neutral functional dynamic equations on time scales[J]. Journal of Northwest Normal University:Natural Science,2015,51(5):12-17.
[22] 杨甲山.具非线性中立项的二阶变时滞微分方程的振荡性[J].华东师范大学学报:自然科学版,2016(4):30-37. YANG J S. Oscillation of second-order variable delay differential equations with nonlinear neutral term[J]. Journal of East China Normal University: Natural Science,
2016(4):30-37.
Kamenev-type oscillation criteria for certain second-order differential equations.
YANG Jiashan1,2, QIN Guijiang1,2
(1.SchoolofInformationandElectronicEngineering,WuzhouUniversity,Wuzhou543002,GuangxiZhuangAutonomousRegion,China; 2.LaboratoryofComplexSystemsSimulationandIntelligentComputing,WuzhouUniversity,Wuzhou543002,GuangxiZhuangAutonomousRegion,China)
We study the oscillatory behavior of a class of second-order variable delay differential equations with a nonlinear neutral term in this article. By using the generalized Riccati transformation and inequality technique, two new Kamenev-type oscillation criteria are presented that can be used in cases when the known results fail to apply. Our results extend and improve some related results reported in the literature.
oscillation; variable delay; nonlinear neutral

2016-06-26.
广西教育厅科研项目(2013YB223);硕士学位授予单位立项建设项目(桂学位[2013]4号);梧州学院2014年校级科研重大项目(2014A003).
杨甲山(1963-), ORCID: http://orcid.org/0000-0002-0340-097X,男,教授,主要从事微分方程的理论与应用研究,E-mail: syxyyjs@qq.com.
10.3785/j.issn.1008-9497.2017.03.005
O 175. 7
A
1008-9497(2017)03-274-07
