平面薄膜天线张拉系统优化设计及天线结构模态分析
2017-05-18刘志全林秋红
刘志全,邱 慧,李 潇,林秋红
(中国空间技术研究院总体部,北京100094)
平面薄膜天线张拉系统优化设计及天线结构模态分析
刘志全,邱 慧,李 潇,林秋红
(中国空间技术研究院总体部,北京100094)
设计航天器平面薄膜天线双重索网张拉系统的构型,并以可伸展支撑杆承受轴力最小、薄膜阵面有效面积比最大、端杆长度最小为优化目标,对张拉系统进行多目标优化。优化后可伸展支撑杆所受轴力减小了15.51%,薄膜阵面有效面积比提高了1.25%,端杆长度减小了0.30%。利用ABAQUS软件对索膜结构、支撑框架以及天线整体的模态分别进行仿真分析,将天线结构等效模型基频的解析解与仿真结果进行比对,二者相互印证。最后通过仿真分析,得出薄膜内拉应力、可伸展支撑杆壁厚、可伸展支撑杆铺层角度和端杆壁厚对天线整体基频的影响规律。
平面薄膜天线;双重索网张拉系统;优化;结构;模态
0 引 言
相对于传统的航天器平面刚性天线[1],柔性平面薄膜天线因质量轻、收拢体积小等优点[2]而成为大型天线(面积达数百平方米甚至更大)的重要发展方向。作为一种新型空间结构,平面薄膜天线备受航天器研制者的关注。平面薄膜天线的薄膜阵面刚度、薄膜阵面有效面积比、支撑框架的受力和支撑框架的尺寸均取决于绳索张拉系统的设计,天线结构模态分析又与该薄膜天线的设计密切相关,所以对大型平面薄膜天线张拉系统开展优化设计、对天线结构进行模态分析均具有重要意义。
薄膜天线张拉系统是薄膜阵面和支撑框架之间的绳索系统,以实现对薄膜阵面施加均匀拉应力及提供薄膜阵面和支撑框架间的柔性连接。目前薄膜天线的张拉系统主要有一级绳索张拉系统[3]和双重索网张拉系统[4]等。一级绳索张拉系统是将薄膜边缘裁剪为曲线索套(花边),绳索穿在索套内,从索套穿出的绳索两端拉紧固连于支撑框架上。双重索网张拉系统包含内索、中间索和外索[4],相比一级绳索张拉系统,双重索网张拉系统具有减小薄膜与支撑框架之间连接点、增大薄膜阵面有效面积比的优点。因此,双重索网张拉系统具有更好的应用前景。
2006年,美国JPL公司Fang等[5]和Fang等[6]将双重索网张拉系统应用到薄膜天线上,以支撑框架受力最小为目标对花边数量、跨距进行了优化,但未涉及中间索长度的优化。 2008年,浙江大学关富玲等[7]基于支撑框架受力最小优化了双重索网张拉系统的薄膜花边数量,给出了奇数跨优于偶数跨的结论,但未涉及花边数量对薄膜阵面有效面积比的影响分析。
国内外也开展了薄膜天线结构的模态分析。2007年,加拿大航天局Shen等[8]利用ABAQUS软件对圆弧花边薄膜进行了模态分析,得出薄膜一阶固有频率(简称基频)与膜内拉应力平方根成正比的结论。2010年,上海交通大学肖薇薇等[9]分析了不同矢跨比(花边曲线弓形高与弦长之比)下单花边矩形薄膜的基频,结果表明薄膜基频随矢跨比减小而降低。2015年,西安电子科技大学刘充等[10]研究了薄膜花边几何参数对薄膜基频的影响,给出了薄膜基频随花边圆心角增大而增大的结论。然而,文献[8-10]并未涉及薄膜天线整体(含薄膜阵面、张拉系统和支撑框架)的模态分析,而天线整体结构的基频及其影响规律更为工程设计所关注。2012年,上海交通大学胡宇[11]虽对薄膜天线整体进行了模态分析,并给出了薄膜拉应力变化比面密度变化对基频影响更大的分析结论,但未涉及对天线整体结构仿真分析结果的验证和支撑框架结构参数对基频的影响分析。
综上,目前张拉系统的优化未涉及中间索的优化,且优化为单目标优化;已有的薄膜天线结构模态分析大多是针对局部结构开展的。针对上述问题,本文拟以支撑框架(主要为可伸展支撑杆[12-13])受力最小、薄膜阵面有效面积比最大和端杆长度最小为优化目标,开展平面薄膜天线双重索网张拉系统的多目标优化设计(含中间索的优化),以获得平面薄膜天线张拉系统结构参数的最优解;利用有限元分析软件ABAQUS对张拉系统优化后的薄膜天线整体进行模态分析,利用天线整体结构等效模型基频的解析解和ABAQUS仿真结果进行互相印证,以获取薄膜内拉应力、可伸展支撑杆壁厚、可伸展支撑杆铺层角度和端杆壁厚对天线整体基频的影响规律。
1 平面薄膜天线双重索网张拉系统的优化设计
1.1 双重索网张拉系统构型的初步设计
平面薄膜天线主要包含:支撑框架、薄膜阵面和张拉系统,其中支撑框架包含端杆、可伸展支撑杆和若干个横杆,如图1所示。
在航天器发射时平面薄膜天线卷曲收拢,当航天器进入预定轨道后,可伸展支撑杆按飞行程序要求展开,从而带动薄膜展开为薄膜阵面结构。依靠薄膜阵面与支撑框架之间的张拉系统保持薄膜阵面所需的刚度和平面度[2]。为了减小支撑框架的受力和横杆的数量并增大薄膜阵面有效面积比,本文将平面薄膜天线张拉系统设计为双重索网张拉系统(下文简称张拉系统) ,如图1所示。与可伸展支撑杆相垂直的均布各横杆与张拉系统中的绳索相连,以避免可伸展支撑杆的受力变形。
张拉系统构型的初步设计如图2所示。
在X轴方向上,绳索分为若干大跨(如图2中的CD折线段或DE折线段),每一大跨中绳索构型如图3所示。
薄膜边缘裁剪为曲线索套(花边),内索穿在索套内,从索套中穿出的内索与中间索相连,中间索与外索连接,外索端点与支撑框架相连,通过对外索端点施加拉力来张紧薄膜。
设薄膜长(X向)为a、宽(Y向)为b,薄膜厚度为t。薄膜X向有x大跨,每一大跨中有N个花边,薄膜Y向有y个花边。则薄膜X向每一大跨的跨度D=a/x。
依据文献[14]的研究结论,当薄膜内的应力状态处于各向等拉应力状态时,薄膜花边为圆弧形。设圆弧花边圆心角为θ,半径为R,当薄膜内拉应力为σ时,内索拉力Tic为[14]
Tic=σtR
(1)
中间索AiBi(i=0,1,2,…,n)拉力Timc均为
Timc=2Ticsin(θ/2)=σtD/N
(2)
设最短中间索A0B0长度为L0,最长中间索AnBn长度为Ln,两者之差Q=Ln-L0,根据文献[4] ,本文推导出:
1)当N为奇数时(N=2n+1),中间索AiBi的长度Li(i=0, 1, 2, …,n)为
(3)
外索AnAn-1上的拉力Tocn最大,其值为
(4)
2)当N为偶数时(N=2n),中间索AiBi的长度Li(i=0, 1, 2, …,n)为
(5)
外索AnAn-1上拉力Tocn为
(6)
式中:Tx为外索AnAn-1上X向的拉力,Ty为外索AnAn-1上Y向的拉力。
从式(3)和式(5)可以看出,只要确定了每个大跨中花边数量N、花边圆弧半径R、最短中间索长度L0以及最长中间索与最短中间索长度之差Q就可确定张拉系统中各部分绳索的长度。
当天线展开后,绳索张紧,从而使膜面产生拉应力,与支撑框架相连的绳索上的拉力使可伸展支撑杆上产生轴力,单根可伸展支撑杆上承受的轴力为
(7)
薄膜阵面有效面积比ω为花边内包络矩形面积与薄膜未裁剪花边前矩形面积之比
(8)
端杆总长度为
Lend=b+2(L0+Q+L0tanβn)
(9)
式中:βn为外索AnAn-1与X轴夹角。
1.2 双重索网张拉系统的多目标优化
平面薄膜天线的可伸展支撑杆为薄壁结构,所受轴力T过大易诱发失稳,所以希望T越小越好;薄膜阵面有效面积比ω越大,电性能越好,所以应尽可能增大ω;端杆长度Lend影响着天线的收纳体积。在保证ω的前提下,缩短中间索长度,可减小Lend,从而减小平面薄膜天线的收纳体积。T、ω和Lend这三者均与张拉系统的结构参数有关,且三者之间相互制约。所以有必要对双重索网张拉系统的结构参数进行多目标优化。
优化数学模型为
minF(Z)=[F1(Z),F2(Z),F3(Z)]
s.t.g(Z)≤0
(10)式中:F1(Z)指单根可伸展支撑杆上承受的轴力,F2(Z)指薄膜阵面有效面积比,F3(Z)指端杆总长度。设计变量Z=[N,R,Q]。花边圆弧需为小圆弧,故约束条件g(Z)为:D/(2N)-R≤0。
将表1的原始数据代入式(10)的优化模型,利用MATLAB的fgoalattain优化函数进行多目标优化。
2.1 第一次记笔记 第一次笔记记载的是课堂教学时的课程内容,一般所占篇幅约为整页纸的2/3。在陈述性知识的新授课中,学生可以采用学案式笔记。

表1 优化所用的原始数据Table 1 Initial data for the optimization
由上述优化模型和原始数据得到优化结果是:当N=35,R=4.290×10-2m,Q=0.2693m时对应的目标函数值为T=11.35N,ω=96.45%,Lend=3.674m。
然而,上述优化过程尚未考虑薄膜花边数量N的影响。若N较大,则张拉系统发生绳索缠绕的概率也同时增大。为了降低张拉系统的复杂性,有必要限制N的取值。图4(a)、(b)、(c)分别展示了T、ω和Lend优化结果随N的变化规律。
由图4可知,随着N逐渐增大,曲线的斜率逐渐降低,当N≥8时,斜率接近0。所以,N最佳取值范围为5~8。根据文献[7]的研究结论,这里取N为奇数7。将N=7代入优化模型重新进行优化,最终获得的最优解为:R= 0.499m,Q=0.293m,优化结果见表2。
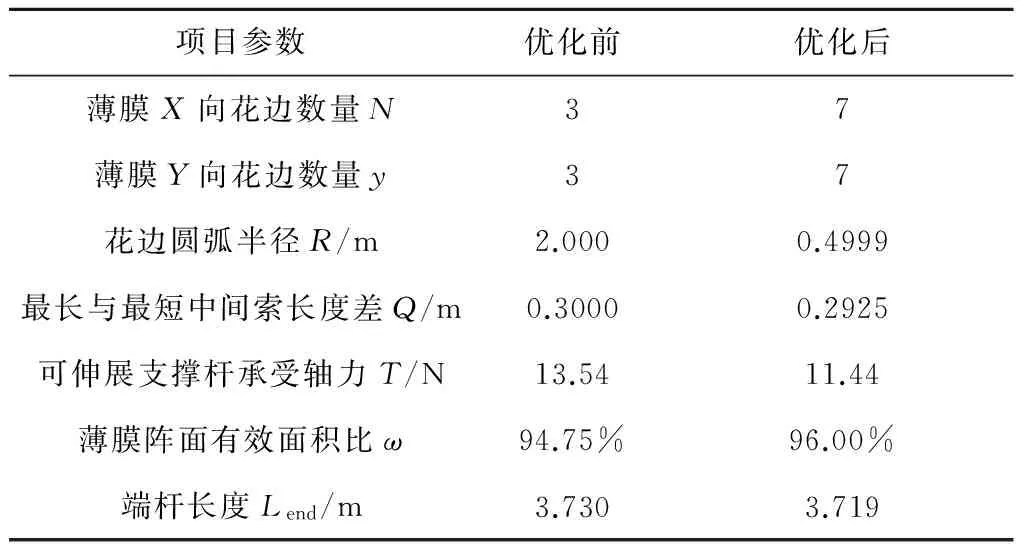
表2 平面薄膜天线张拉系统优化前后对比Table 2 Comparison of parameters before and after optimization
从表2可以看出,相对于张拉系统的初步设计,多目标优化后T减小了15.51%,ω提高了1.25%,Lend减小了0.30%。
应当指出,图2所示的张拉点C、D、E处的受力情况均为汇交力系,存在静不定问题。为将此静不定问题转化为静定问题,对C、D、E处的索网结构进行局部修改,如图5所示。
针对调整后的张拉系统,重新计算了T、ω和Lend(此处不再赘述)。结果表明,T和Lend的结果与上文的结果保持不变,仅ω的数值有所下降,但与上文的结果的差值约为0.05%,可忽略不计。
2 平面薄膜天线结构的模态分析
2.1 平面薄膜天线中索膜结构的模态分析
索膜结构中的张拉系统为上文优化后的双重索网张拉系统。本文索膜结构中薄膜和绳索材料的性能参数如表3所示。
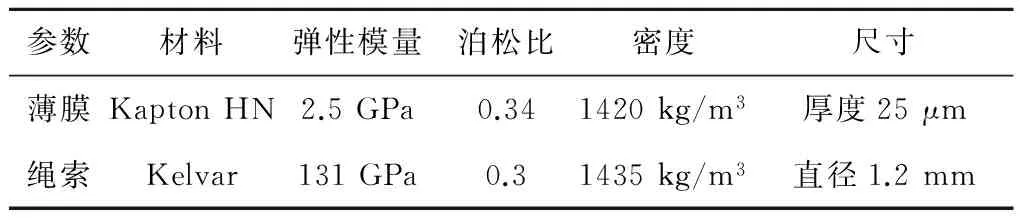
表3 索膜结构各部分材料参数Table 3 Material parameters of cable-membrane structure
在ABAQUS软件中建立索膜结构模型,用膜单元(M3D3)模拟薄膜阵面;用杆单元(T3D2)模拟绳索,花边和绳索之间的连接用绑定约束。模态分析分为两步:1)对索膜结构进行静力分析,通过张拉外索将拉应力导入到薄膜和绳索中;2)固定外索张拉点,对有拉应力的索膜结构进行模态分析。分析结果表明,当σ=0.08MPa时,索膜结构的基频f1cm=1.0609Hz。
2.2 平面薄膜天线中支撑框架的模态分析
支撑框架中的端杆和横杆分别为壁厚1mm的矩形(100mm×50mm)薄壁管和圆形(外径15mm)薄壁管。
可伸展支撑杆为特殊截面的复合材料薄壁管,由5层复合材料铺设而成,铺层角度为45°/-45°/0°/-45°/45°,每层厚度tb=0.04mm。其中,每层碳纤维复合材料的材料参数为:弹性模量E1=114.38GPa,E2=7.06GPa,剪切模量G12=2.96GPa,泊松比ν12=0.289,密度ρ=1600kg/m3。
在ABAQUS软件中建立支撑框架模型。其中,可伸展支撑杆用叠层复合材料建模,且采用壳单元(S4R)对其进行模拟[13]。端杆和横杆均为各向同性材料薄壁管,用壳单元(S4)进行模拟。固定可伸展支撑杆中间,对支撑框架进行模态分析。分析得到支撑框架基频f1b=0.9454Hz。
由叠层复合材料的本构关系可计算出可伸展支撑杆的轴向等效弹性模量。本构关系式[15]为
(11)
式中:P和M分别为截面单位宽度的内力和内力矩,ε0为中面应变,k为中面曲率变化向量,A、B、H分别为叠层材料的拉压刚度矩阵、拉(压)弯(扭)耦合刚度矩阵和弯曲(扭转)刚度矩阵。
对于对称铺层,B=0,即不存在拉(压)弯(扭)耦合效应。根据单层材料的刚度矩阵和铺层角度,可算出A和H,分别为
可见,H的值相对于A的值很小,且B=0,因此可忽略弯曲刚度和扭转刚度。将A代入式(11),可得到叠层复合材料的应力-应变关系。最终可得到5层复合材料的面内等效工程弹性系数为:E1,eq=31.94GPa,E2,eq=18.34GPa,G12,eq=25.19GPa,ν12,eq=0.802。
因支撑框架为对称结构,取其1/4进行分析。可伸展支撑杆可等效为一根悬臂梁,端杆等效为悬臂梁端点的集中质量,横杆等效为悬臂梁上中点处的集中质量。可伸展支撑杆为复合材料薄壁管,根据上文计算,可忽略此复合材料的面外刚度。最终,该悬臂梁的基频为[16]
(12)
式中:Eb、Ib、Lb、mb分别为可伸展支撑杆的轴向等效弹性模量、横截面惯性矩、半长、1/2质量,mend为端杆质量之半,mbar为横杆质量之半。其值分别为:Eb=31.94GPa,Ib=79.064×10-9m4,Lb=5.475m,mb=0.875kg,mend=1.055kg,mbar=0.290kg。
由式(12)计算得到的支撑框架等效模型的基频为0.9479Hz,与上文仿真得到的支撑框架基频0.9454Hz相比,二者差别仅0.264%,从而支撑框架的仿真结果和等效模型基频的解析解互为印证。
2.3 平面薄膜天线整体模态分析
天线整体模态分析分为两步:1)分别对支撑框架和索膜结构进行静力分析,对外索张拉点施加相应的拉力,得到索膜结构和支撑框架的应力状态。2)用ABAQUS软件中的Initial State命令(初始状态导入)将静力分析得到的各部分的应力导入,然后固定可伸展支撑杆的中间,对天线整体进行模态分析,仿真得到天线整体结构的基频f1ante=0.8826 Hz。
由第2.1节可知,当σ=0.08MPa时,索膜结构的基频f1cm=1.0609Hz,比支撑框架基频(f1b=0.9454Hz)高12.22%,故可把索膜结构近似等效为支撑框架上的均布质量。根据薄膜的长宽比a/b,可把索膜结构总质量(mmem+mcable)的b/(a+b)分配给端杆,作为端杆上的均布质量;把索膜结构总质量(mmem+mcable)的a/(a+b)分配给可伸展支撑杆,作为可伸展支撑杆上的均布质量。横杆质量不变。故加上分配的均布质量后的端杆质量mend1和可伸展支撑杆的质量mb1分别为
(13)
(14)
式中:mmem为整个薄膜质量的1/4,mcable为所有绳索质量的1/4,其值分别为mmem=1.120kg,mcable=9.540×10-2kg。
当把索膜结构等效为支撑框架上的均布质量后,天线整体结构就可简化为具有等效质量的支撑框架,进而由第2.2节的方法简化为一根在端点和中部有集中质量的悬臂梁。故可用式(13)和式(14)所获得的mend1和mb1分别替换式(12)中的mend和mb,然后由式(12)计算天线整体结构等效模型的基频。该基频计算结果为0.8776Hz,与上文仿真得到的f1ante=0.8826Hz相比,二者差别仅0.570%,从而使得天线整体结构基频的仿真结果和等效模型基频的解析解互为印证。
2.4 平面薄膜天线结构参数对基频的影响分析
1) 薄膜内拉应力σ对基频的影响
在ABAQUS软件中,保持支撑框架结构参数不变,改变薄膜内拉应力σ的大小,分别分析索膜结构、支撑框架和天线整体结构的基频,可得到基频f1cm、f1b、f1ante随薄膜内拉应力σ的变化,如图6所示。
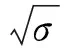
图7分别展示了σ为0.01、0.08和0.25MPa时天线整体的一阶振型。从图7可以看出,当σ=0.01MPa时,天线的振动主要来自于索膜结构;当σ=0.08MPa时,天线的振动来自于索膜结构和支撑框架两者;当σ=0.25MPa时,天线的振动主要来自于支撑框架。
2) 可伸展支撑杆壁厚tboom对基频的影响
若保持σ=0.08MPa不变,改变tboom大小,则基频f1cm、f1b和f1ante随tboom的变化曲线见图8(虽然索膜结构的基频f1cm与tboom没有关系,图8中表示出f1cm的变化曲线主要是为了展示f1cm、f1b和f1ante三者之间的关系,下文中的图9~10均与此类似)。
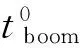
3) 可伸展支撑杆铺层角度γ对基频的影响
若保持σ=0.08MPa不变,改变γ大小,则基频f1cm、f1b和f1ante随γ的变化如图9所示。
由图9可知,索膜结构的基频f1cm始终保持不变(1.0609Hz)。当γ≤45°时,随γ增大,支撑框架基频f1b减小,且减小速率较大;当γ>45°后,f1b减小速率放缓;当γ≥60°时,f1b基本保持不变。设当铺层角度为γ0时,f1cm=f1b。则天线整体结构的基频f1ante在γ<γ0时有微下降的趋势;且当γ=γ0左右时,f1ante减小速率加大,随后f1ante减小速率逐渐放缓,最后f1ante基本保持不变。
4) 端杆壁厚tend对基频的影响
若保持σ=0.08MPa不变,改变tend大小,则基频f1cm、f1b和f1ante随tend的变化如图10所示。
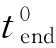
3 结 论
针对本文的平面薄膜天线模型,开展了双重索网张拉系统的多目标优化以及平面薄膜天线结构的模态分析,获得了如下结论:
1) 张拉系统经多目标优化后可伸展支撑杆承受轴力减小了15.51%,薄膜阵面有效面积比提高了1.25%,端杆长度减小了0.30%。张拉系统结构参数的最优解见表2。该结论是基于文中表1原始数据获得的,对于其它平面薄膜天线双重索网张拉系统,本文的优化模型和方法具有普适性,但优化结果会有所不同。
2) 天线整体结构的基频f1ante近似等于索膜结构和支撑框架两者中基频较低者。并有以下规律:
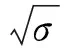
(3) 设当铺层角度为γ0时,f1cm=f1b。则天线整体结构的基频f1ante在γ<γ0时有微下降趋势;且当γ=γ0左右时,f1ante减小速率加大,随后f1ante减小速率逐渐放缓,最后f1ante基本保持不变。
[1] 李春升,王伟杰,王鹏波,等. 星载SAR技术的现状与发展趋势[J]. 电子与信息学报,2016,38(1): 229-240. [Li Chun-sheng, Wang Wei-jie, Wang Peng-bo, et al. Current situation and development trends of spaceborne SAR technology [J]. Journal of Electronics & Information Technology, 2016, 38(1): 229-240.]
[2] Lopez B C, Lou M C, Huang J, et al. Development of an inflatable SAR engineering model [C]. 42nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Seattle, USA, April 16-19, 2001.
[3] Lin J K H, Cadogan D P, Feria V A, et al. An inflatable microstrip reflectarray concept for Ka-band applications [C]. 41st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, USA, April 3-6, 2000.
[4] Sakamoto H, Miyazaki Y, Park K C. Evaluation of cable suspended membrane structures for wrinkle-free design [C]. 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, USA, April 7-10, 2003.
[5] Fang H, Lou M, Hsia L M, et al. Catenary systems for membrane structures [C]. 42nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference and Exhibit, Seattle, USA, April 16-19, 2001.
[6] Fang H, Huang J, Quijano U, et al. Design and technologies development for an eight-meter inflatable reflectarray antenna [C]. 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Newport, USA, May 1-4, 2006.
[7] 关富玲,汪有伟,杨超辉. 新型折叠卷收式反射阵天线的设计与制作[J]. 工程设计学报,2008,15(6): 466-471. [Guan Fu-ling, Wang You-wei, Yang Chao-hui. Design and fabrication of new type reflect array antenna [J]. Journal of Engineering Design, 2008, 15(6): 466-471.]
[8] Shen Y, Zheng W, Wang X. Dynamic and vibration analysis of a SAR membrane antenna [C]. 2007 ASME International Mechanical Engineering Congress and Exposition, Seattle, USA, November 11-15, 2007.
[9] 肖薇薇,陈务军,付功义.空间薄膜阵面预应力导入效应及影响因素[J].宇航学报,2010,31(3): 845-849. [Xiao Wei-wei, Chen Wu-jun, Fu Gong-yi. Pre-stress introduction effects and influence factors investigation for the space planar film reflect-array [J]. Journal of Astronautics, 2010, 31(3): 845-849.]
[10] 刘充,李玉宇,保宏,等.边界几何参数对空间平面张拉膜结构固有频率影响研究[J]. 振动与冲击,2015,34(20): 198-202. [Liu Chong, Li Yu-yu, Bao Hong, et al. Natural frequencies of pre-tensioned membrane structure with different boundary geometrical parameters [J]. Journal of Vibration and Shock, 2015, 34(20): 198-202.]
[11] 胡宇. 空间薄膜阵面预应力及结构特性分析[D]. 上海: 上海交通大学,2012. [Hu Yu. Analysis of pre-stress and structural characteristic of space film reflect-array [D]. Shanghai: Shanghai Jiao Tong University, 2012.]
[12] 张展智,赵国伟,焦景勇,等. 空间薄壁式伸展臂的展开仿真与卷曲方式研究[J]. 宇航学报,2013,34(3): 299-307. [Zhang Zhan-zhi, Zhao Guo-wei, Jiao Jing-yong, et al. Deployment simulation and coiling method study of a space thin-wall deployable boom [J]. Journal of Astronautics, 2013, 34(3): 299-307.]
[13] 李瑞雄,陈务军,付功义. 透镜式薄壁CFRP管空间伸展臂轴压屈曲分析及试验[J]. 宇航学报,2012,33(8): 1164-1170. [Li Rui-xiong, Chen Wu-jun, Fu Gong-yi. Buckling analysis and experiment of lenticular CFRP thin-walled tube space boom under axial compression [J]. Journal of Astronautics, 2012, 33(8): 1164-1170.]
[14] Greschik G, White C V, Salama M A. On the precisely uniform and uniaxial tensioning of a film sheet via integrated catenary [C]. 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, USA, April 7-10, 2003.
[15] 陈烈民,杨宝宁.复合材料的力学分析[M]. 北京:中国科学技术出版社,2006:98-104.
[16] 胡海岩. 机械振动基础[M]. 北京:北京航空航天大学出版社,2005:100-106.
通信地址:北京市5142信箱408分箱(100094)
电话:(010)68747342
E-mail: liuzhiquanymj@sina.com
(编辑:牛苗苗)
Optimal Design of Catenary System and Model Analysis for a Planar Membrane Antenna Structure
LIU Zhi-quan, QIU Hui, LI Xiao, LIN Qiu-hong
(Institute of Spacecraft System Engineering, China Academy of Space Technology, Beijing 100094, China)
The double catenary system is designed for a planar membrane antenna. A multi-objective optimization strategy is applied to the catenary system, which exhibits the improvement of following three design objectives. The optimization result shows that the force loaded to the boom reduces by 15.51%, the percentage of the effective area for the membrane increases by 1.25% and the hub length reduces by 0.30%. Furthermore, the model of the cable-membrane structure, the frame and the whole antenna structure is analyzed by the software ABAQUS. The fundamental frequency simulation results of the antenna structure are compared with the analytic solutions based on the equivalent model, and the results are verified. Finally, the influence law of the membrane stress, deployable boom thickness, fabric layers angle of the deployable boom and wall thickness of the hub on the fundamental frequency of the whole antenna structure is revealed.
Planar membrane antenna; Double catenary system; Optimization; Structure; Model
2016-12-14;
2017-02-18
V414
A
1000-1328(2017)04-0344-08
10.3873/j.issn.1000-1328.2017.04.003
刘志全(1963-),男,研究员,博士生导师,主要从事航天器结构与机构技术、可靠性技术等方面的研究。
