广义变分模态分解及其在齿轮箱复合故障诊断中的应用

杨 宇 罗 鹏 程军

圣湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

广义变分模态分解及其在齿轮箱复合故障诊断中的应用

杨 宇 罗 鹏 程军

圣湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

针对变分模态分解在实际应用过程中需要根据先验知识确定惩罚函数和分量分解个数这一缺陷，提出了一种改进方法，即广义变分模态分解方法。该方法减少了人为因素对分解结果造成的主观影响，将信号分解转化为非递归、变分模态分解方式，能够有效分离频率成分相近的谐波分量，且对信噪比较小的信号有着良好的鲁棒性。将该方法应用于齿轮箱复合故障诊断中，仿真和实验的结果验证了该方法的有效性。

广义变分模态分解；齿轮箱；复合故障诊断；特征提取

0 引言

旋转机械设备的大部分工作状态都会以振动的形式表现出来，因此，采集设备的振动信号并对其进行相应的处理就能提取得到故障特征,但是随着设备的机构复杂化，采集得到的振动信号往往表现出非线性、非平稳特征[1]，传统的时域分析和频域分析方法不能有效提取其故障特征，而时频分析方法作为一种有效的信号处理方法，已经成为旋转机械故障诊断的重要手段。

经验模态分解(empirical mode decomposition，EMD)作为一种自适应信号处理方法，在齿轮箱等机械设备故障诊断中有着广泛应用[2-3]，但它存在模态混叠以及端点效应的短板，因而在实际故障诊断中的应用受到限制[4]；集合经验模态分解(ensemble empirical mode decomposition，EEMD)对于模态混叠现象有着一定程度上的抑制作用，但EEMD计算量较大，添加的白噪声不能被完全中和，不具有完备性[5-6]；变分模态分解(variational mode decomposition，VMD)将信号分解转化为非递归、变分模态分解方式，在很多方面相对于传统方法表现出更加优良的性能[7-10]，比如，它能够成功将频率成分相近的谐波分量分离，对噪声信号有着良好的鲁棒性,但是VMD算法的信号处理结果同时受惩罚参数和分量分解个数的影响[11-12]，在运用该方法进行分解时需要人为设定这两个参数，而在工程实际中，由于采集得到的信号成分分量个数未知，同时惩罚参数的选择也是随工况变化而变化的，这就给实际故障诊断应用带来了不便。

针对VMD方法的缺陷，本文提出了一种改进方法，即广义变分模态分解(generalized variational mode decomposition,GVMD)方法，该方法克服了VMD方法受信号分量个数以及惩罚参数影响的不足，同时又能够解决模态混叠的问题，特别是对于频率成分相近的信号分离有着十分显著的效果。运用仿真信号对比分析了GVMD与EEMD以及VMD方法的分解结果，最后将GVMD方法运用到齿轮箱复合故障仿真及实验信号处理之中，成功将故障信号从原始信号中分离出来。

1 广义变分模态分解

GVMD方法的核心思想就是将信号分解成有限个模态函数之和，通过对变分问题的求解使得每个模态的估计带宽最小。其中，约束变分问题描述如下：

(1)式中,uk为分解得到的有限个分量,k∈[1,K]；ωk为各分量的频率中心；δ(t)为脉冲函数；f为原始信号；t为时间序列；K为模态函数个数，由给定求解精度ε确定。

利用傅里叶等距变换，将式(1)转换到频域，得到各模态的频域更新：

(2)

运用模态函数功率谱重心法可得中心频率的更新公式：

(3)

对于给定求解精度ε(根据运算次数和精度综合考虑，ε取10-7)，满足下式时迭代终止：

(4)

GVMD的具体实现过程如下：

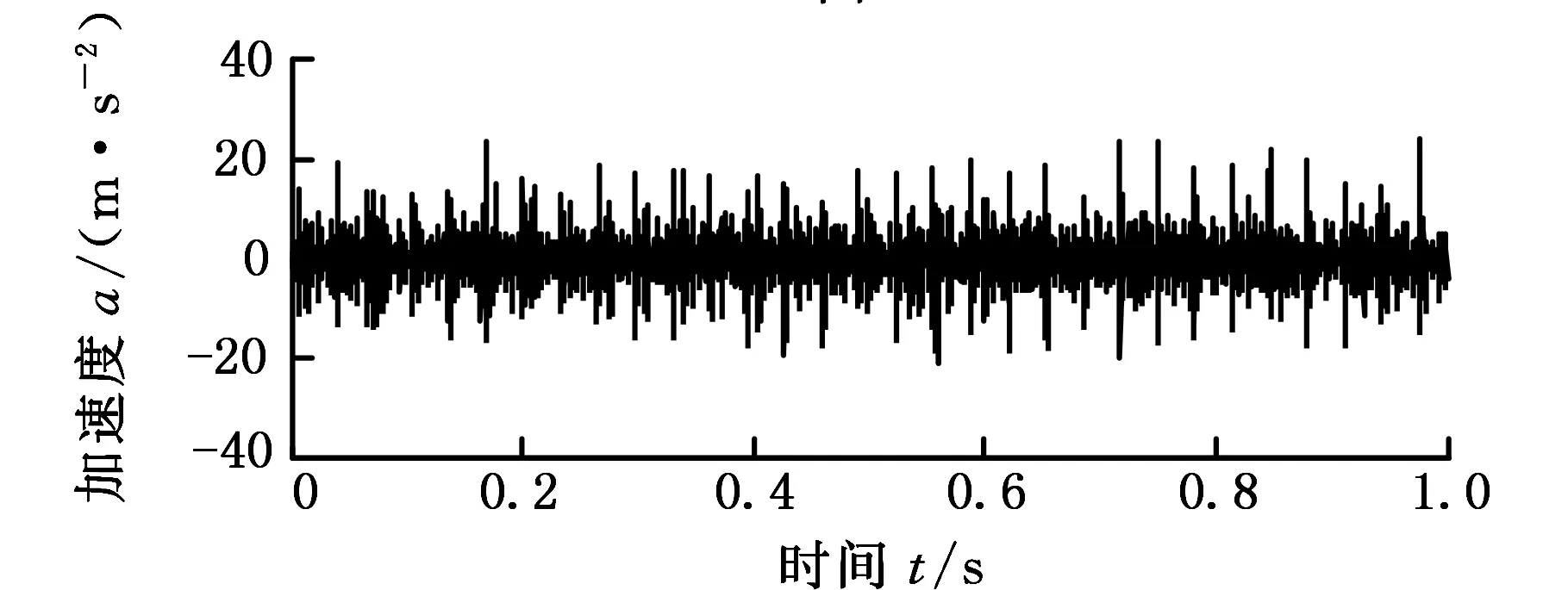
(3)根据式(4)判断收敛性，若不满足条件且n

2 仿真分析

为了说明GVMD的优越性，需要将其与现有的信号分解方法进行对比分析。在解决信号频率混叠以及端点效应方面，EEMD及VMD有着公认的优势，基于此种考虑，同时为了节约篇幅，避免不必要的重复比较，本文将GVMD与EEMD及VMD方法进行了对比。

为不失一般性，本文选择三个频率成分不同的谐波信号之和进行仿真分析，原始信号以及各分量如下：

f(t)=x1(t)+x2(t)+x3(t)

(5)

x1(t)=sin(200πt)

(6)

x2(t)=0.5sin(160πt)

(7)

x3(t)=0.3sin(20πt)

(8)

采样频率为1024Hz，仿真时间为1s，三个分量的频率分别为100Hz、80Hz、10Hz。原始信号以及分量时域图形如图1所示，其中，As为原始信号幅值，x1、x2、x3分别为三个分量对应幅值。EEMD、VMD及GVMD分解结果分别如图2～图4所示，其中，i1～i5为EEMD分解5个分量信号对应幅值，r为残余信号幅值，u1、u2、u3为VMD分解3个分量信号对应幅值，g1、g2、g3为GVMD分解3个分量信号对应幅值。

图1 原始信号及三个分量的时域波形图Fig.1 Time domain waveform of the original signal and three components

图2 EEMD分解结果Fig.2 EEMD decomposition results

图3 VMD得到三个分量的时域图形Fig.3 Temporal graph of VMD decomposition results

图4 GVMD得到三个分量的时域图形Fig.4 Temporal graph of the GVMD decomposition results

从分解得到的结果可得出以下结论：EEMD仍然存在较为严重的频率混叠现象，分解结果不能较好地满足要求；VMD能够将三个分量分离，但是存在较明显的端点效应；而GVMD将三个信号有效分离，并且端点效应得到了有效的抑制。

对仿真信号以及EEMD、VMD和GVMD分解得到的分量分别求解相应的Hilbert谱(f1、f2、f3、f4分别为对应幅值)，如图5所示。

图5 仿真信号、EEMD、VMD和GVMD分解结果的 Hilbert谱Fig.5 Hilbert spectra of the simulation signal, EEMD, VMD and GVMD decomposition results

从EEMD得到的分解结果来看，分量i1、i2、i3包含信号x1和x2，求其频谱可以发现，出现频率混叠现象，i5近似为信号x3，但从其时频谱中可以看出存在端点失真现象；而VMD虽然将三种不同频率的信号分离开来，但也存在明显的端点效应；GVMD得到的三个分量的Hilbert谱显示与原始信号Hilbert谱一模一样。因此可以发现，与现行的时频分析方法相比，GVMD方法确实有着一定的优越性。

为了进一步验证分解信号与真实信号的吻合程度，本文以相对误差能量和相关系数作为评价指标。两种分解方法得到的结果见表1。可以清楚地看到，无论是相对误差能量还是相关系数，采用GVMD方法所得结果的准确度均高于采用VMD方法所得结果的准确度。

表1 两种方法得到的分量与真实值的误差和相关性Tab.1 Error and correlation between the two components and the real value

3 齿轮箱复合故障仿真分析及实验信号验证

3.1 齿轮箱复合故障仿真分析

在旋转机械中，齿轮和滚动轴承是两个重要的组成部件,因此，本文在模拟齿轮箱复合故障时就采用齿轮故障仿真信号和滚动轴承故障仿真信号来进行模拟，分别设置齿轮和滚动轴承的故障仿真信号如下：

x1(t)=(1+cos(2πfrt))sin(2πfzt)

(9)

(10)式中，fr为齿轮幅值调制频率；fz为载波频率；M为轴承周期冲击个数；Bm为第m个冲击信号的幅值大小；β为衰减系数；fn为共振频率；TP为模拟冲击间隔，即模拟滚动轴承故障特征频率f0=1/TP；u(t)为单位阶跃函数。

为模拟滚动轴承和齿轮的仿真特性，先设定故障仿真信号各参数，见表2。

表2 故障仿真信号参数Tab.2 Parameters of the fault simulation signal

设置仿真信号采样频率fs=8192Hz，采样点数为8192，采样时间为1s，模拟的滚动轴承故障频率f0。代入上述参数，生成相应的仿真信号。

将齿轮故障仿真信号和滚动轴承故障仿真信号叠加到一起，模拟齿轮箱复合故障，然后运用GVMD方法将复合信号进行分解，得到的结果如图6所示。对分解结果进行包络谱分析，得到的结果如图7所示，可以清楚地看到GVMD得到的两分量确实就是齿轮故障信号和滚动轴承故障信号。

图6 复合故障信号及其GVMD结果Fig.6 Compound fault signal and its GVMD results

图7 GVMD得到两分量的包络谱Fig.7 Envelope spectrum of the two components obtained by GVMD

3.2 齿轮箱复合故障实验分析

为验证GVMD方法的有效性，将该方法运用于实际旋转机械复合故障诊断中。在旋转机械故障模拟试验台上对一个齿轮和滚动轴承设置模拟故障，实验中采用SKF6307-2RS深沟球轴承，齿轮为直齿轮，主动轮和从动轮齿数均为37。在齿轮上切割掉一个齿来模拟断齿故障，在滚动轴承外圈切割宽0.15 mm、深0.13 mm的槽来模拟滚动轴承故障。实验中采用振动加速度传感器，安装于故障轴承座上，采样频率fs=8192Hz，轴的转速为600r/min，即转频fr=10Hz，滚动轴承的外圈故障频率f0=31Hz。

将采集到的复合故障信号进行包络谱分析，得到的结果如图8所示。从包络谱分析可知，复合故障包含滚动轴承外圈故障，但是齿轮故障信息则完全被淹没。

(a)复合故障时域信号

(b)包络谱图8 复合故障振动信号及其包络谱Fig.8 Compound fault vibration signal and its envelope spectrum

运用GVMD方法对实验信号进行分解，得到的结果如图9所示；然后对两分量分别进行包络谱分析，得到的结果如图10所示。从齿轮包络谱中可以看到，10Hz的频率突出，与齿轮故障特征频率相符；在轴承包络谱中可以看到,存在31Hz及其倍频突出，这与滚动轴承外圈故障特征相对应。因此，GVMD方法能够为齿轮箱复合故障诊断提供有效依据。

图9 GVMD得到的两分量Fig.9 Two components of GVMD

图10 GVMD得到两分量的包络谱Fig.10 Envelope spectrum of the two components obtained by GVMD

4 结论

广义变分模态分解克服了变分模态分解的缺陷，可以避免分量个数以及惩罚参数的选择，减小了主观误差。该方法对于近频谐波信号的分离有着显著的效果，能够有效解决因频率混叠而导致有用信号丢失的问题。实验结果说明该方法能够为复合故障的诊断提供有效依据。

[1] 曾鸣, 杨宇, 郑近德, 等.μ-SVD降噪算法及其在齿轮故障诊断中的应用[J]. 机械工程学报,2015, 51(3):95-103.ZENGMing,YANGYu,ZHENGJinde,etal.μ-SVDBasedDenoisingMethodandItsApplicationtoGearFaultDiagnosis[J].JournalofMechanicalEngineering,2015,51(3):95-103.

[2] 杨宇,于德介,程军圣,等.基于经验模态分解包络谱的滚动轴承故障诊断方法[J]. 中国机械工程,2004,15(16):1469-1471.YANGYu,YUDeijie,CHENGJunsheng,etal.AFaultDiagnosisApproachforRollerBearingsBasedonEMDandEnvelopeSpectrum[J].ChinaMechanicalEngineering,2004,15(16):1469-1471.

[3] 郑近德,程军圣.改进的希尔伯特-黄变换及其在滚动轴承故障诊断中的应用[J]. 机械工程学报,2015,51(1):138-145.ZHENGJinde,ChengJunsheng.ImprovedHilbert-HuangTransformandItsApplicationstoRollingBearingFaultDiagnosis[J].JournalofMechanicalEngineering,2015,51(1):138-145.

[4] 杨望灿,张培林,王怀光,等.基于EEMD的多尺度模糊熵的齿轮故障诊断[J]. 振动与冲击,2015,34(14):163-167.YANGWangcan,ZHANGPeilin,WANGHuai-guang,etal.GearFaultDiagnosisBasedonMultiscaleFuzzyEntropyofEEMD[J].JournalofVibrationandShock,2015,34(14):163-167.

[5] 郑近德,程军圣,杨宇,等.改进的EEMD算法及其应用研究[J]. 振动与冲击,2013,32(21):21-26.ZHENGJinde,CHENGJunsheng,YANGYu,etal.ModifiedEEMDAlgorithmandItsApplications[J].JournalofVibrationandShock,2013,32(21):21-26.

[6] 位秀雷,林瑞霖,刘树勇,等.小波-SG-EEMD混合算法及混沌去噪应用研究[J]. 振动与冲击,2015,34(17):100-104.WEIXiulei,LINRuilin,LIUShuyong,etal.HybridWavelet-SG-EEMDAlgorithmandItsApplicationinChaoticDe-noising[J].JournalofVibrationandShock,2015,34(17):100-104.

[7]DRAGOMIRETSKITYK,ZOSSOD.VariationalModeDecomposition[J].IEEETransactionsonSignalProcessing,2014,62(3):531-544.

[8] 石敏,李影,王冰,等.基于变分模态分解的齿轮箱故障诊断[J]. 电力科学与工程,2016,32(1):23-26.SHIMin,LIYing,WANGBing,etal.GearboxFaultDiagnosisBasedonVariationalModeDecomposition[J].ElectricPowerScienceandEngineering,2016,32(1):23-26.

[9] 刘长良,武英杰,甄成刚,等.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报,2015,35(13):3358-3365.LIUChangliang,WUYingjie,ZHENChenggang,etal.RollingBearingFaultDiagnosisBasedonVariationalModeDecompositionandFuzzyCMeansClustering[J].ProceedingsoftheCSEE,2015,35(13):3358-3365.

[10] 唐贵基,王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报,2015,49(5):73-81.TANGGuiji,WANGXiaolong.ParameterOptimizedVariationalModeDecompositionMethodwithApplicationtoIncipientFaultDiagnosisofRollingBearing[J].JournalofXi’anJiaotongUniversity,2015,49(5):73-81.

[11] 付文龙,周建中,张勇传,等.基于OVMD与SVR的水电机组振动趋势预测[J]. 振动与冲击,2016,35(8):36-40.FUWenlong,ZHOUJianzhong,ZHANGYongchuan,etal.VibrationTrendPredictionofHydroelectricGeneratingUnitBasedonOVMDandSVR[J].JournalofVibrationandShock,2016,35(8):36-40.

[12] 高雷阜,齐微.结合权余量和粒子群方法求解变分优化问题[J]. 计算机工程与应用,2011,47(30):26-28.GAOLeifu,QIWei.CombiningRightSurpluswithParticleSwarmMethodtoSolveVariationalOptimizationProblems[J].ComputerEngineeringandApplications,2011,47(30):26-28.

(编辑 陈 勇)

GVMD and Its Applications in Composite Fault Diagnosis for Gearboxes

YANG Yu LUO Peng CHENG Junsheng

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082

According to the defects of the VMD that its penalty parameters and number of components were based on the prior knowledges in the processes of the actual applications, based on the VMD an improved method, namely, the GVMD was proposed herein. This method held the potentials to overcome the deciencies of VMD, and it might reduce the subjective influences on the decomposition results. By decomposing the signal into non recursive and variational modal, the method might effectively separate the harmonic frequency components that were similar to each other and had good robustness. It was applied in the composite fault diagnosis of the gearboxex, and the simulation results and test verify the validity of this method.

generalized variational mode decomposition(GVMD); gearbox; composite fault diagnosis; feature extraction

2016-07-08

国家重点研发计划资助项目(2016YFF0203400)；国家自然科学基金资助项目(51575168，51375152)；智能型新能源汽车国家2011协同创新中心、湖南省绿色汽车2011协同创新中心资助项目

TH113

10.3969/j.issn.1004-132X.2017.09.011

杨 宇，女，1971年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。主要研究方向为动态信号处理、机电设备状态监控与故障诊断、模式识别等。E-mail：yangyu@hnu.edu.cn。罗 鹏，男，1989年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。程军圣，男，1968年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。