基于改进Tent映射的自适应变尺度混沌粒子群算法
2017-05-16李国晓韦世丹
李国晓,韦世丹
(广东水利电力职业技术学院,广东 广州 510635)
基于改进Tent映射的自适应变尺度混沌粒子群算法
李国晓,韦世丹
(广东水利电力职业技术学院,广东 广州 510635)
为改善标准粒子群优化算法本身存在的缺陷,引入种群混沌初始化方法、参数自适应调整策略、早熟判断机制以及基于改进Tent 映射的变尺度混沌局部搜索方法对原有算法进行改进,提出一种基于改进Tent映射的自适应变尺度混沌粒子群算法(Improved Adaptive Chaos PSO,IACPSO)。多种高维Benchmark函数的计算结果表明,IACPSO算法在计算精度、优化稳定性及收敛速度方面均明显优于其他改进粒子群优化算法。
粒子群优化算法;Tent映射;变尺度;混沌;自适应
0 引 言
粒子群优化算法(Particle Swarm Optimization,PSO)是一类基于群智能的演化计算方法。该算法在低维空间的函数优化问题上具有求解速度快、质量高等优点,但若问题解的维数增加,其优化性能便急剧下降,易陷入局部最优解。针对PSO算法本身存在的缺陷,国内外学者已提出诸多改进方案,这些方案大致可以分为3类:第1类是对PSO参数(惯性权重w、学习因子c1与c2)进行调整与改进,如线性递减权重法[1]、压缩因子法[2]、动态惯性权重法[3]等,这些方法在某种程度上较好地解决了PSO算法早熟收敛问题,但参数的选择具有随机性,需要进行大量的数据试验,并且与具体应用存在较大联系;第2类是在PSO算法中引入各种变异机制以保持粒子寻优的多样性,这类方法主要为防止粒子在求解空间内过早陷入局部最优解,但是粒子多样性的提高会影响到PSO算法的收敛速度[4];第3类是在PSO算法中融入其他智能算法以增强粒子的局部开发能力,如与遗传、差分进化等算法的结合[5-6]。
针对标准PSO算法易陷入局部最优、迭代后期收敛较慢等问题,本文提出了一种基于改进Tent映射的自适应变尺度混沌粒子群算法(Improved Adaptive Chaos PSO,IACPSO)。首先,该算法将改进Tent映射产生的混沌序列对种群位置与速度进行赋值,以提高初始种群个体质量及粒子分布的多样性;其次,对惯性权重及学习因子采用自适应调整策略,以均衡算法在求解空间内的全局与局部搜索能力;最后,配合早熟判断机制及基于改进Tent映射的变尺度混沌局部搜索策略,以进一步提高算法求解精度及收敛速度。
1 IACPSO算法的主要思想
1.1 标准粒子群优化算法(SPSO)
标准粒子群优化算法(SPSO)算法可描述为:在D维求解空间,第i个粒子根据个体极值Pi=(pi,1,pi,2,…,pi,D)与全局极值Pg=(pg,1,pg,2,…,pg,D)动态调整自身的位置Xi=(xi,1,xi,2,…,xi,D)与速度Vi=(vi,1,vi,2,…,vi,D)。求解前需对各粒子的位置和速度进行初始化,在第t次迭代时,粒子按下式更新下代的速度和位置[7]
vi,d(t+1)=wvi,d(t)+c1r1[pi,d(t)-xi,d(t)]+c2r2[pg,d(t)-xi,d(t)]
(1)
xi,d(t+1)=xi,d(t)+vi,d(t+1)
(2)
式中,i=1,2,…,M;d=1,2,…,D;vi,d∈[-vdmax,vdmax];xi,d∈[xmin,d,xmax,d];M为粒子个数;D为求解空间的维数;w为惯性权重;c1和c2为学习因子;r1和r2为均匀分布在[0,1]的随机数。
1.2 基于改进Tent映射的种群混沌初始化
种群的初始化对PSO算法的全局收敛速度及解的质量产生重要影响。在没有任何先验信息可利用的情况下,种群的位置与速度一般采用随机初始化的方法产生初始解。随机初始化方法虽在一定程度上能保证初始种群分布均匀,但不能保证个别粒子质量,部分群体可能远离最优解,故影响算法收敛速度。利用混沌序列对粒子位置与速度进行初始化,既能不影响PSO算法初始化时所拥有的随机性本质,又能利用混沌序列特性提高种群的多样性及粒子搜索的遍历性[8]。与传统混沌优化算法常采用的Logistic映射相比,改进Tent映射具有更优越的混沌特性,能更好地实现混沌寻优[9]。本文采用改进Tent映射对种群位置与速度进行初始化,其表达式为
(3)
式中,k为混沌迭代次数,k=0,1,…,Cmax;当xk=0、0.25、0.5、0.75或xk=xk-m,m={0,1,2,3,4}时,则根据式(3)重新赋值
(4)
1.3 参数自适应调整策略
惯性权重w是影响算法优化性能的重要参数,合理选择w可使粒子具有均衡的全局与局部搜索能力。为此,本文采用一种根据粒子当前适应度自动调整w的方法,其表达式为
(5)
式中,wmax、wmin分别为w的最大值与最小值;fi为粒子当前适应度;favg与fmin分别为当前所有粒子的平均适应度和最小适应度。
学习因子c1和c2分别体现了个体粒子的自我探索与群体学习能力。在算法寻优初期,粒子应具有较大的自我探索能力和较小的群体学习能力,以加强粒子的全局搜索能力;在寻优后期,粒子应具有较小的自我探索能力与较大的群体学习能力,以保证粒子倾向于全局极值。为此,学习因子c1和c2可采用如下调整策略
(6)
式中,c1max、c2max分别为c1和c2的最大值;c1min、c2min分别为c1和c2的最小值;t为当前迭代次数;Tmax为最大迭代次数。
1.4 早熟判断机制
随着算法迭代次数的增加,个体之间的差异性将逐渐降低,而粒子位置的一致性则等价于各粒子具有相同的适应度值,故可根据种群中全体粒子适应度值的整体变化来判断种群的收敛状态。为此,本文采用群体适应度方差σ2作为早熟判断机制,其反映的是粒子群中个体粒子的聚集程度,计算公式为[10]
(7)
式中,M为种群规模的大小;f为归一化因子,其作用是限制σ2的大小,表达式为
(8)
1.5 基于改进Tent映射的变尺度混沌局部搜索
为提高算法求解精度及收敛速度,可将变尺度混沌优化算法[11]与SPSO算法相结合,利用混沌运动所具有的随机性、遍历性等特点,在部分较优粒子周围执行局部搜索,帮助这些粒子搜寻到更优解。同时,搜索范围将随迭代次数的增加而逐渐缩小,以提高混沌变量的搜索效率。变尺度混沌局部搜索的主要步骤如下:
(9)
式中,m为已执行局部搜索次数;pi,d′为第i个较优粒子Pi′=(pi,1′,pi,2′,…,pi,D′)第d维分量;φ为收缩因子,其表达式为
(10)
(11)
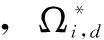
(12)
式中,β为自适应调节系数,其表达式为
β=1-((t-1)/t)η
(13)
式中,η为正整数,可根据目标函数而定。
(3)将cxd′按下式转化为新的决策变量xd′
(14)
(4)根据新解Xi′=(pi,1′,…,xi,d′,…,pi,D′)计算其适应度f(Xi′)。若f(Xi′)

表1 Benchmark函数
1.6 IACPSO算法的实现方法
结合基于改进Tent映射的种群混沌初始化方法、早熟判断机制、参数自适应调整策略以及变尺度混沌局部搜索策略,构建出基于改进Tent映射的自适应变尺度混沌粒子群算法(IACPSO)。完整的IACPSO算法的实现方法可归纳为:
(1)设置算法参数。利用改进Tent映射混沌模型对各粒子的速度与位置进行初始化。
(2)初始参数下,计算各粒子个体适应度fi,确定并保存群体最优位置Pg及个体最优位置Pi。
(3)根据式(5)、(6)调整惯性权重与学习因子,按式(1)、(2)更新各粒子的速度和位置,重新计算各粒子个体适应度并更新Pg与Pi。
(4)根据式(7)计算群体的适应度方差σ2。若σ2低于阈值δ,则对个体适应度前20%的粒子执行变尺度混沌局部搜索,搜索完成后转至(3);否则直接转至(3)。
(5)若算法满足终止条件(本文以最大迭代次数为限制条件),则寻优结束,否则转至(3)。
2 IACPSO算法优化性能分析
2.1 试验设置
为验证本文提出的IACPSO算法的函数优化性能,选取PSO算法常用的6个Benchmark函数进行优化试验。表1给出了各函数的名称、表达式、最优值及搜索范围。其中,f1、f2与f3为单峰函数;f4、f5与f6为多峰函数。同时,将IACPSO算法与相同环境下的惯性权重线性递减的PSO算法[12](LDWPSO)、基于Logistic映射的混沌PSO算法[13](CPSO)进行比较分析。计算平台为Matlab R2009b,算法采用M语言编程实现。
各算法的运行参数设置如下:IACPSO算法中,wmax=0.9,wmin=0.4,c1max=c2max=2.5,c1min=c2min=0.5,阈值δ=10,适应度阈值fδ=0.1,η1=0.5,η2=10 000,混沌迭代次数Cmax=10;LDWPSO算法中,惯性权重w由0.9线性递减至0.4,c1=c1=1.5;CPSO算法中,其惯性权重、混沌迭代次数与IACPSO一致。此外,各算法的种群规模N=30,最大迭代次数Tmax=2 000。各算法的终止条件为当前算法获得的优化值低于表1所对应函数的最优值或者达到最大迭代次数。
2.2 算法优化性能比较及分析
采用平均值(Mean)和标准差(Std)作为各个算法的性能测试与比较指标。其中,Mean用来衡量算法的求解精度;Std用来衡量算法的稳定性与鲁棒性。表2给出了LDWPSO、CPSO与IACPSO算法对Benchmark函数f1~f6分别在10、20与30维空间中独立运行30次的优化性能比较结果。其中,粗体字表示相同指标下比较结果的相对最优值。
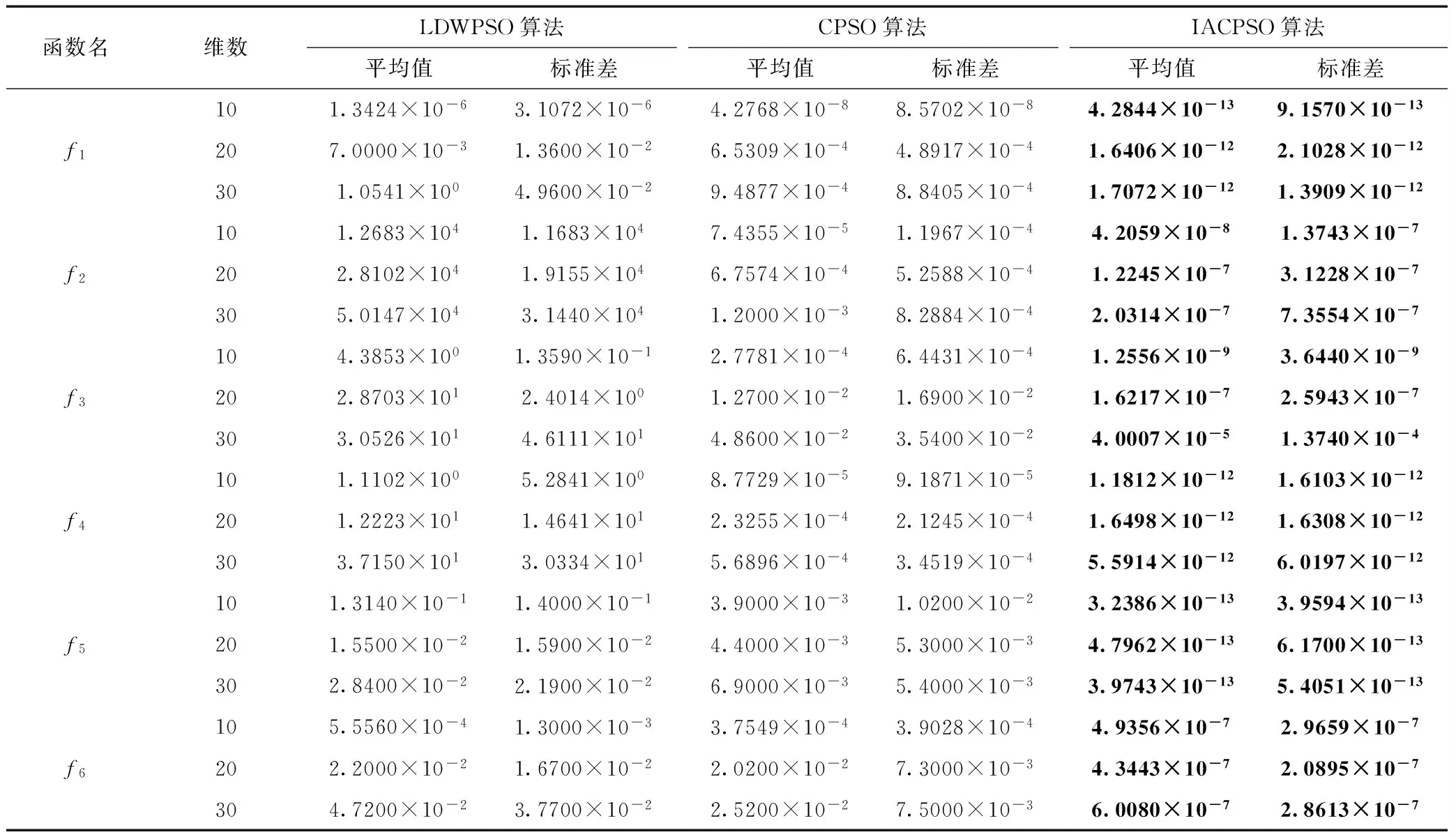
表2 LDWPSO、CPSO与IACPSO算法的优化性能比较结果
由表2中的相同维数下Benchmark函数测试结果可知,相较于LDWPSO与CPSO算法,IACPSO算法对Benchmark函数f1~f6的求解质量相对较高,尤其是对多峰函数f4与f5,其Mean与Std值均远低于其他2种算法。由此可见,IACPSO算法具有更高的求解精度及更好的计算稳定性。此外,随着Benchmark函数维数的增加,其复杂性逐渐提高,此时LDWPSO与CPSO算法的Mean与Std值均有不同程度的上升,表明上述2种算法对Benchmark函数的求解精度及计算稳定性逐渐变差,且给算法的收敛带来较大困难;然而,与LDWPSO、CPSO算法不同的是,Benchmark函数维数变化对IACPSO算法的Mean与Std值影响较小,IACPSO算法始终保持较高的求解精度及计算稳定性。
为更加直观地反映出IACPSO算法的函数寻优效果,图1给出了LDWPSO、CPSO及IACPSO算法对30维Benchmark函数进行30次独立试验的平均适应度值收敛曲线。从图1可知,IACPSO算法的初始平均适应度值略低于LDWPSO及CPSO算法,这是由于基于改进Tent映射的种群混沌初始化方法能有效提升IACPSO算法初始解的质量,一定程度上提高了初始种群的多样性及粒子搜索的遍历性。此外,除函数f4之外,IACPSO算法无论处于迭代初期还是后期,其收敛速度均明显快于LDWPSO与CPSO算法,且经过一定迭代次数之后,LDWPSO与CPSO算法均过早地陷入早熟收敛状态,而此时IACPSO算法却可以非常稳健地向全局最优解的方向继续寻优下去,最终IACPSO算法的求解精度远高于LDWPSO与CPSO算法。究其原因,主要是由于IACPSO算法中采用了参数自适应调整策略及基于改进Tent映射的变尺度混沌局部搜索策略。上述2种策略的引入使IACPSO算法拥有更高的搜索效率及更快的收敛速度,在处理Benchmark函数时能很快跳出局部最优解,极大增加了算法收敛到全局最优解的可能性。
综上可知,本文提出的IACPSO算法具有较为平衡的全局搜索及局部开发能力,在计算精度、优化稳定性及收敛速度方面均明显优于LDWPSO与CPSO算法。
3 结 语
为改善标准粒子群优化算法求解复杂优化问题时收敛速度慢及容易早熟收敛等缺陷,本文提出了一种融合有种群混沌初始化方法、早熟判断机制、参数自适应调整策略及变尺度混沌局部搜索策略的自适应变尺度混沌粒子群优化算法。对多种高维Benchmark 函数的计算结果表明,本文所提出的IACPSO算法在计算精度、优化稳定性及收敛速度方面均明显优于LDWPSO与CPSO算法。
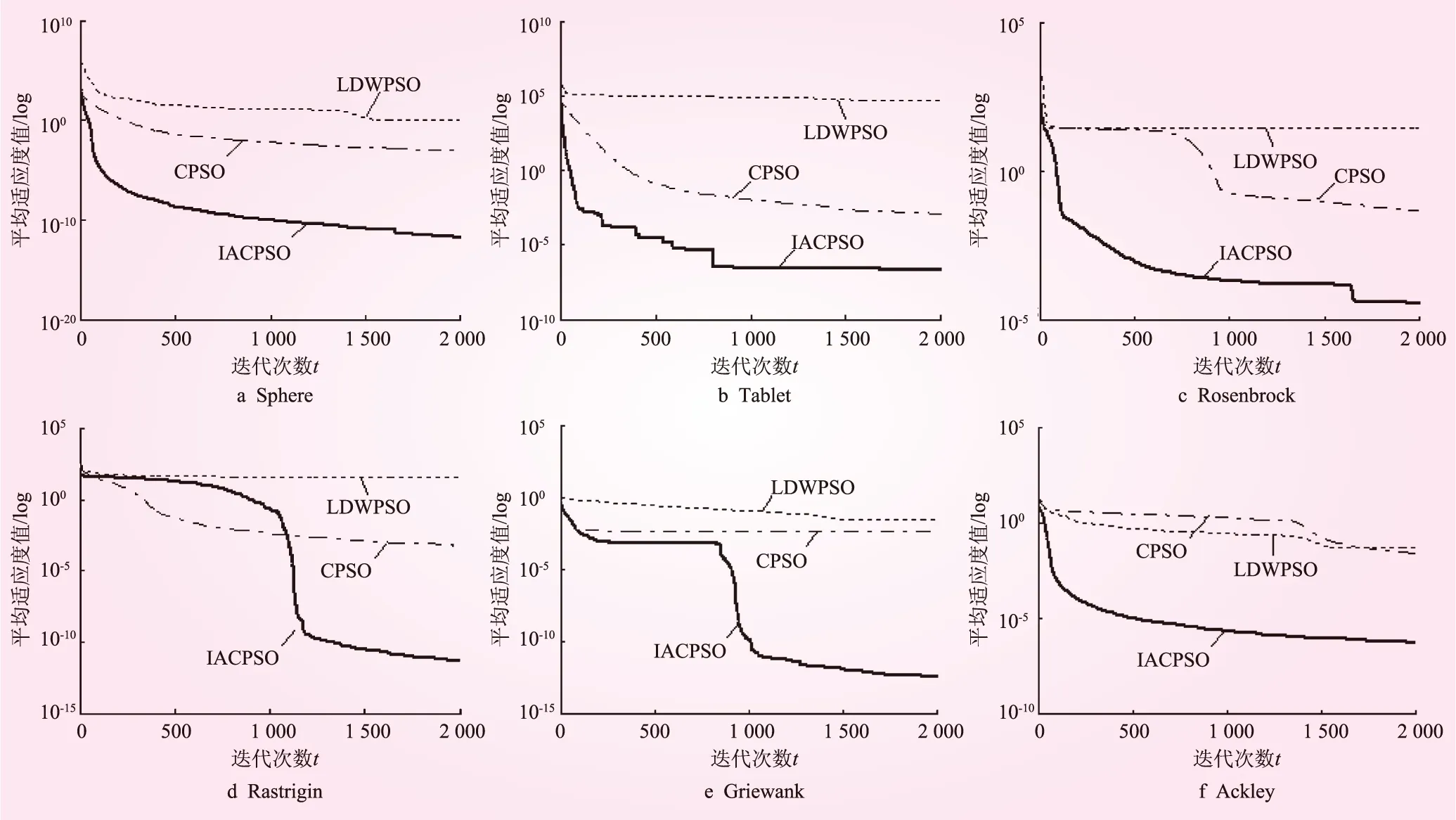
图1 30维Benchmark函数的平均适应度值收敛
[1]SHI Y, EBERHART R. A modified particle swarm optimizer[C]∥Proceedings of the 1998 Congress on Evolutionary Computation. Piscataway: IEEE Press, 1998: 69-73.
[2]CLERC M.The swarm and the queen: Towards a deter-ministic and adaptive particle swarm optimization[C]∥Proceedings of the 1999 Congress on Evolutionary Computation. Piscataway: IEEE Press, 1999: 1951-1957.
[3]EBERHART R, SHI Y. Particle swarm optimization: developments, applications and resources[C]∥Proceedings of the 2001 Congress on Evolutionary Computation. Piscataway: IEEE Press, 2001: 81-86.
[4]CHENG S, SHI Y H. Diversity control in particle swarm optimization[C]∥IEEE Symposium on Swarm Intelligence. Piscataway: IEEE Press, 2011: 1-9.
[5]XIN B, CHEN J, ZHANG J. Hybridizing differential evolution and particle swarm optimization to design powerful optimizers: A review and taxonomy[J]. IEEE Trans on Systems,Man and Cybernetics,Part C: Applications and Reviews, 2012, 42(5): 744-767.
[6]BO Y. A hybrid evolutionary algorithm by combination of PSO and GA for unconstrained and constrained optimization roblems[C]∥IEEE Int Conf on Control and Automation. Piscataway: IEEE Press, 2007: 166-170.
[7]KENNEDY J, EBERHART R. Particle swarm optimization[C]∥Proceedings of the 1995 IEEE International Conference on Neural Networks, Piscataway: IEEE Press, 1995: 1942-1948.
[8]王维博, 冯全源. 基于分层多子群的混沌粒子群优化算法[J]. 控制与决策, 2010, 25(11): 1663-1668.
[9]王瑞琪, 张承慧, 李珂. 基于改进混沌优化的多目标遗传算法[J]. 控制与决策, 2011, 26(9): 1391-1397.
[10]王小根, 龙海侠, 孙俊. 基于高斯扰动的量子粒子群优化算法[J]. 计算机应用研究, 2010, 27(6): 2093-2096.
[11]张彤, 王宏伟, 王子才. 变尺度混沌优化算法及其应用[J]. 控制与决策, 1999, 14(3): 285-288.
[12]SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]∥Proc of the 1999 Congress on Evolutionary Computation. Piscataway: IEEE Press, 1999: 1945-1950.
[13]LIU B, WANG L, JIN Y H, et al. Improved particle swarm optimization combined with chaos[J]. Chaos, Solitons and Fractals, 2005, 25(5): 1261-1271.
(责任编辑 杨 健)
An Improved Adaptive Chaos Particle Swarm Optimization Algorithm Based on Improved Tent Map
LI Guoxiao, WEI Shidan
(Guangdong Polytechnic of Water Resources and Electric Engineering, Guangzhou 510635, Guangdong, China)
In order to improve the defect of basic Particle Swarm Optimization algorithm, an Improved Adaptive Chaos Particle Swarm Optimization (IACPSO) algorithm based on improved Tent map is proposed herein, which including population chaos initialization method, adaptive parameter adjusting strategy, precocious judgment mechanism and mutative scale chaos local search based on improved Tent map. The results of some high-dimensional Benchmark functions show that the IACPSO algorithm is better than other improved PSO on computation accuracy, optimization stability and convergence speed.
Particle Swarm Optimization algorithm; Tent map; mutative scale; chaos; adaptive
2016-06-28
李国晓(1977—),男,河南襄城人,讲师,硕士,主要从事水电站动力设备教学与研究工作.
TP301.6
A
0559-9342(2017)02-0089-05
