基于最短路径的旅游咨询网站的设计与应用

董妍汝

(山西大学商务学院信息学院，山西 太原 030031)

基于最短路径的旅游咨询网站的设计与应用

董妍汝

(山西大学商务学院信息学院，山西 太原 030031)

为了满足旅行者和旅行社对旅游景点最短路径查询的需求，采用Dijkstra算法实现了四种基本查询方式，满足用户对旅游景点间的最优路径查找，并设计了基于最短路径的旅游咨询网站。文中首先对所采用的算法进行了简单介绍，然后以山西省的旅游景点为例对网站的查询功能进行了详细阐述，最后对采用Dijkstra算法后的路径选择性能进行分析。

最短路径；Dijkstra算法； 旅游咨询

随着生活节奏的加速和能源的紧缺，无论是对与旅行者还是旅行社而言，旅游路线都是其关注的重中之重。对于旅行者而言，希望在旅行中能够以最小的时间成本和金钱成本满足最大化的消费需求；对旅行社而言，期望满足客户的同时尽可能地降低成本，从而提高其效益[1]。因此，本文采用最短路径算法设计并实现旅游咨询网站，将旅游景点之间的路线进行定量的分析，使旅行者和旅行社得到相对合适的旅游路线，从而合理的安排旅游行程，满足各自的需求。

1 最短路径算法

考虑到为用户提供最优路径能节省用户的旅行时间和经费，也能够间接地节省能源，本文采用经典的Dijkstra算法获取景点间的最短路径[2]。Dijkstra算法是贪婪法应用的一个例子，主要用来解决单个源点到其它顶点的最短路径。

Dijkstra算法按照路径“长度”递增的次序产生最短路径[3]。该算法将图G(V,E)中的顶点分成两个集合VA、VB，如果源点S到某一个顶点的最短路径已经确定，则该顶点属于VA，反之，则属于VB。初始时，VA中只有源点S，其余的顶点均在VB中，算法结束时，源点可以直接或间接到达的顶点均属于VA，源点不能到达的顶点留在VB中。

2 基于最短路径算法的旅游咨询网站设计

本文以山西省的旅游景点为例，设计基于最短路径算法的旅游咨询网站，分别从以下三个方面对该网站进行介绍。

2.1 网站功能的设计

该网站主要功能是为用户提供山西省各地区风景名胜详细介绍的同时，为网站用户提供最短路径查询，主要包括以下查询方式：

1) 用户输入起点，可以显示起点到山西各旅游景点的最短旅游线路，供用户对比选择。

2) 用户输入起点、终点，可以显示这两地之间的最短旅游线路。

3) 用户输入起点、意向旅游的若干景点，可以为用户提供一条包含这些景点的最短旅游线路。

4) 用户输入起点、意向旅游的景点、终点，为用户规划一条从起点到终点并途经用户意向旅游景点的最短路线。

以上查询方式不仅实现了任意两个旅游景点间的最短旅游路线查询，对多个特定旅游景点间的最短路径也可进行查询，实现了路径的智能查询[4]。

2.2 旅游景点最短路径的算法

以云冈石窟，悬空寺，应县木塔，五台山，晋祠，平遥古城这六个旅游景点为例进行各种最短路径的规划。为方便起见，依次用V0，V1，V2，V3，V4，V5表示这六个旅游景点，即云冈石窟V0，悬空寺V1，应县木塔V2，五台山V3，晋祠V4，平遥古城V5。根据这六个景点的分布图，已知这些景点之间的距离(该距离按照二级公路来计算)，构造出如图1所示的带权无向图。

1) 单个旅游景点到其它景点间的最短路径查询

图1 带权无向图

当用户想了解云冈石窟到其它五个景点的最短旅游线路时，用户可以进入网站的查询页面，在“起点”中输入云冈石窟，单击查询，可以得到以下查询结果：从V0到各个结点的最短路径为：V0-V1；V0-V2；V0-V2-V3；V0-V4；V0-V4-V5。即从云冈石窟出发到五台山，经过应县木塔的路径是最短的；同理，从云冈石窟出发到平遥古城，经过晋祠的路径是最短的。

运用第二部分中描述的Dijkstra算法，可以求得从结点V0(即云冈石窟)到各个结点的最短路径。如表1所示，表中展示了每次寻找当前不属于S集合的，并且具有最短路径的顶点的过程。其中，粗黑色方框中表示的就是从结点V0到各个结点的最短路径以及该路径的长度。

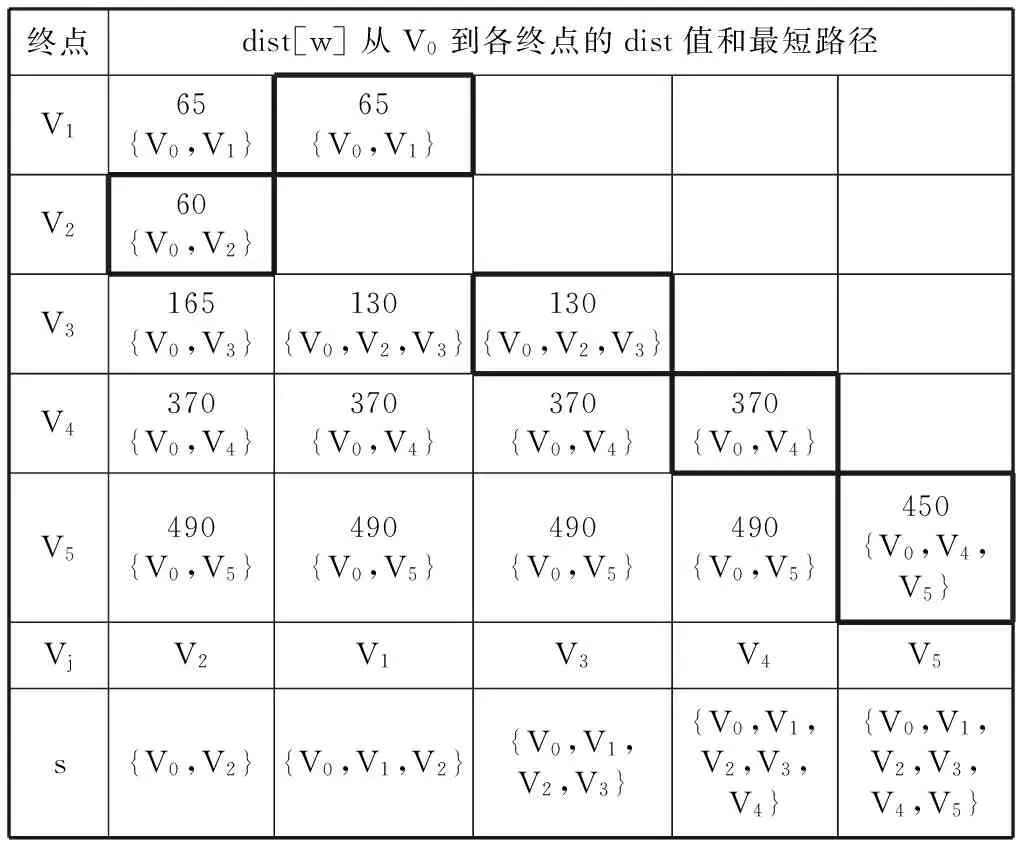
表1 从V0到各终点的dist值和最短路径示意

该查询功能是Dijkstra算法的直接应用。通过上述的例子可以知道，运用该算法即可求得从某一旅游景点到其余各景点的最短路径，从而可在一定程度上节省游客的旅行经费和时间。

2) 两个旅游景点间的最短路径查询

当用户想查从悬空寺(V1)去晋祠(V4)的最短旅游路径时，可在查询页面的“起点”输入悬空寺，“终点”输入晋祠，单击查询，可得到查询结果：悬空寺—五台山—晋祠。

第二种查询方式的实现与第一种查询方式相同，以用户输入的“起点”悬空寺(V1)为源点，执行Dijkstra算法，算出悬空寺(V1)到各旅游景点的最短路径，只是在显示结果时只提供给用户悬空寺(V1)到晋祠(V4)的最短路径。

3) 多个旅游景点之间的最短路径查询

如果用户从悬空寺(V1)出发，希望得到一条经过云冈石窟(V0)、应县木塔(V2)、晋祠(V4)的最短旅游线路，可在查询页面的“起点”中输入悬空寺，“途经”输入云冈石窟、应县木塔、晋祠，单击查询，得到查询结果：悬空寺—云冈石窟—应县木塔—五台山—晋祠。

第三种查询方式是求多点之间的最短路径，即全局最优解。Dijkstra算法只能用于求两点之间的最短路径，不能解决这个问题，在此，采用Dijkstra算法寻求局部最短路径，从而形成全局较优路径。

首先以用户输入的“起点”为源点，寻找该源点到“途经”地各景点的最短路径，找出离“起点”最近的景点。继续以此景点为源点，寻找该源点到剩余“途经”地各景点的最近景点，直到所有的“途经”景点都寻找完毕。为了使查询的结果能接近全局最优解，将刚才的查找过程再逆序执行遍，即以最后一次找到的景点为源点，用户输入的“起点”为终点，寻找全局最优路径。这两次查找的路径有可能是不一样的，其中最短的路径就是最终提供给用户的查询结果。具体步骤及流程图如图2。

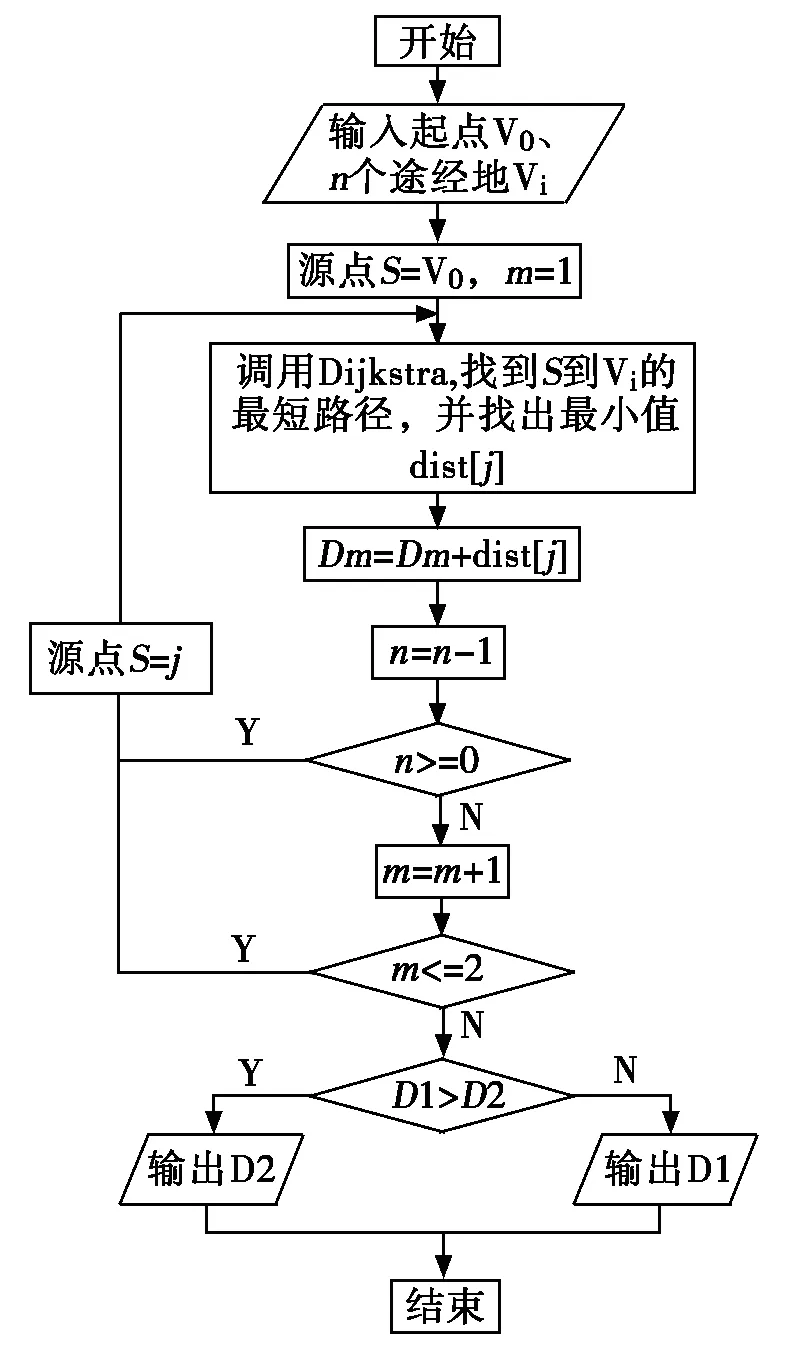
图2 多景点最短路线查询流程图

定义集合VA中存放已经找到最小路径的顶点，初始值为源点S，集合VB中存放所有顶点，集合VC中存放用户“途经”的顶点。dist[i]表示到顶点Vi的最短路径。D表示最终的最短路径。

第一步：以用户输入的“起点”为源点S；

第二步：调用Dijkstra算法在集合VB中寻找S到集合VC所有顶点的最短路径，并找到其中的最小值dist[j]。

dist[j]=min{dist[i]|( Vi∈VB)}

D1=D1+ dist[j]

第三步：将顶点j从集合VB、VC中删除，放入集合VA。

第四步：判断VC是否为空，如果为空，则表示正向查找完毕，结果为D1，继续执行第五步。否则返回第二步。

第五步：以最后经过的顶点为源点，开始逆向查询。查询的结果为D2。

第六步：如果D1

4) 确定起点和终点的多景点最短路径查询

如果用户想了解从悬空寺(V1)出发，终点到云冈石窟(V0)，途经应县木塔(V2)，晋祠(V4)的最短旅游路径，可在查询页面的“起点”中输入悬空寺，“终点”输入云冈石窟，“途经”输入应县木塔，晋祠，单击查询，可以得到查询结果：V1-V3-V4-V3-V2-V0。

这种查询方式与第三种查询方式类似，都是用Dijkstra算法寻求局部最短路径，从而形成全局较优路径。查询时，以用户输入的“起点”为源点，进行一次正向查询，再以用户输入的“终点”为源点，进行一次逆向查询。比较两次查询结果中路径的长度，如果正向查询的结果小，则输出该线路，如果逆向查询的结果小，则逆序输出路径中的顶点。

3 基于最短路径算法的旅游咨询网站性能

用户使用景点间最短路径咨询的功能后，可以在一定程度上节省旅行时间和经费。例如在前面的例子中，用户欲获取从云冈石窟到平遥古城的最短路径(即顶点V0到V5)。从顶点V0到V5有多条路径，如V0-V4-V5，V0-V1-V2-V3-V5，V0-V5，V0-V2-V3-V5，V0-V1-V3-V4-V5，分别记为路径1，路径2，路径3，路径4，路径5。通过对数据库的查询与简单的计算，可知这五条路径各自的全程长度：路径1=520公里，路径2=450公里，路径3=490公里，路径4=470公里，路径5=480公里。

据调查，普通小轿车每100公里需要耗油约为10升，旅行客车每100公里需要耗油约为22升。若按油价为6.5元/升来计算，可以得到普通小轿车和旅行客车分别行驶这五条路径所需的汽油费用。同理，假定在高速公路上汽车行驶的速度为80公里/小时，也可以得到普通小轿车和旅行客车分别行驶这五条路径所需的时间。如表2所示。

表2 行驶五条路径消耗费用和时间表

由上述分析可知，选择顶点V0到V5的最短路径(即V0-V4-V5，路径2)，即从云冈石窟出发到平遥古城，经过晋祠的路径(全程450公里)，这要比从顶点V0直接到达V5(即V0-V5，路径3)，即从云冈石窟直接到平遥古城(全程490公里)少行驶40公里的路程。在采用最短路径经算法后，对于普通小轿车可节省油费约26元；对于旅行客车来说可节省油费约57.2元，可节省时间约30分钟。从上述数据可以看出将最短路径算法应用于旅游咨询网站中具有一定的可行性。

4 结束语

本文将最短路径算法应用在旅游咨询网站中，并对该网站的相关功能、算法及数据库进行了设计。同时，以山西省旅游景点为例，对设计的具有最短路径咨询功能的旅游网站进行实验分析。通过分析可知，将该算法应用在旅游咨询网站中，可以使用户根据各自不同的需求对景点间的最短路径进行咨询的同时，节省游客的旅行经费和宝贵的时间。

[1] 黄心,吴学群,袁清冽.蚁群算法在外卖配送路径规划中的应用[J].价值工程,2017(5):65-67.

[2] 张靓.基于子集优化的Dijkstra算法的交通最短路径查询系统的设计与实现[D].长春：吉林大学,2015.

[3] 王树西,李安渝.Dijkstra算法中的多邻接点与多条最短路径问题[J].计算机科学,2014(6):217-224.

[4] 胡乔楠.基于旅游文记的旅游景点推荐及行程路线规划系统[D].杭州：浙江大学,2015.

[5] 乔天斐.基于Android平台的自助旅游系统研究与实现[D].成都：电子科技大学,2016.

[6] 饶亚玲.基于客流疏导的景区游览线路优化研究[D].泉州：华侨大学,2015.

[7] 郑外辉.符合游客口味的旅游路线分析技术研究与应用[D].杭州：浙江大学,2015.

[8] 左为平,刘云芳.Dijkstra算法在最短旅游路径中的应用[J].计算机与信息技术,2011(增刊2):41-42.

The Design and Application of Tourism Consultation Website Based on Shortest Path Algorithm

Dong Yanru

(InformationProjectDepartment,BusinessCollegeofShanxiUniversity,TaiyuanShanxi030031,China)

In this paper, Dijkstra algorithm is used for finding the optimal path among the tourist attractions to satisfy the travelers and travel agencies’ needs. Thus the Tourism Consultation Website based on the shortest path algorithm is designed. Firstly, the paper makes a brief description on the relevant algorithm, then, taking Shanxi tourist spot for example, it expounds the function of design. Finally it analyzes the performance of the path selection after the relevant algorithm is adopted.

shortest path; Dijkstra algorithm; tourism consultation

2016-03-15

董妍汝(1981- )，女，山西运城人，副教授，研究生，研究方向：计算机应用。

1674- 4578(2017)02- 0045- 04

TP393

A