基于广义ICOWA算子和最大-最小贴近度的区间型组合预测模型
2017-05-16潘瑞袁宏俊
潘瑞,袁宏俊
(安徽财经大学统计与应用数学学院,安徽 蚌埠 233000)
基于广义ICOWA算子和最大-最小贴近度的区间型组合预测模型
潘瑞,袁宏俊
(安徽财经大学统计与应用数学学院,安徽 蚌埠 233000)
将最大-最小贴近度和广义诱导连续有序加权平均算子结合,应用于区间数的预测问题,建立了基于最大-最小贴近度的广义ICOWA算子的区间组合预测模型.同时提出了优性区间组合预测、非劣性区间组合预测、劣性区间组合预测、冗余方法和冗余度等概念,并针对该模型建立了评价体系,最后通过实例分析,得出该区间组合预测是合理有效的.
最大-最小贴近度;广义ICOWA算子;区间组合预测;评价体系
20 世纪60年代,Bates J.M.和Granger C.W.J.[1]首次创造性地提出了组合预测方法的理论和方法.这种方法综合利用了多种预测方法提供的信息,取得的预测结果比各单项预测方法更为接近现实状况,即有更高的预测精度,同时也能提高预测的稳定性.国内外的很多学者都比较热衷这种方法的研究与应用,并取得了大量的研究成果.在组合预测领域的发展前期,学者们主要集中于对点的预测,即实际值和预测值只涉及一个数值;而现实生活中对某个指标的描述常常涉及到一个区间范围,因此区间组合预测的概念应运而生.目前的组合预测模型大多是以误差指标和相关性指标为最优化准则,常见的相关性指标一般包括相关系数、Theil不等系数、向量夹角余弦和灰色关联度.贴近度是近期出现的一种相关指标.汪新凡和杨小娟[2]讨论了联系数贴近度的定义和性质,然后基于逼近理想解的排序方法( TOPSIS),将联系数贴近度应用于由区间数决策矩阵转化的联系数决策矩阵,提出了一种崭新的区间数多属性决策方法.杨春玲等[3]提出区间数贴近度的概念并讨论了它的相关性质,然后基于这种贴近度构建一种新的不确定多属性决策模型.袁宏俊和杨桂元[4]引进最大—最小贴近度,建立了基于该相关指标的最优组合预测模型,并且通过实例分析,表明该方法的合理有效性.组合预测模型中应用的算子也有很多种,Yager[5~6]提出了诱导有序加权平均算子(IOWA算子)和连续区间有序加权平均算子(COWA算子),金飞飞[7]将这两种算子相结合,提出了诱导连续区间有序加权平均算子(ICOWA算子),建立了基于ICOWA算子的区间组合预测模型.
在对ICOWA算子进行研究后,本文将ICOWA算子拓展为广义的ICOWA算子,并与最大-最小贴近度相结合运用到区间数的组合预测上,提出了基于最大-最小贴近度的广义ICOWA算子的区间组合预测模型.为更好地评价该种模型对实际情况的预测效果,建立了相应的评价体系,提出优性区间组合预测、非劣性区间组合预测、劣性区间组合预测、冗余方法和冗余度等概念,并且通过实例分析,得出该种模型是合理有效的.
1 基本概念
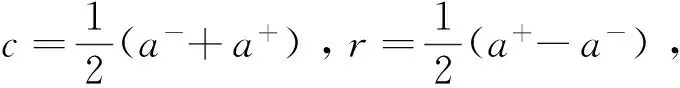
定义2[5~6]:设[a,b]为区间数,令
(1)
则称fρ为连续区间上的OWA算子,简称COWA算子.式中ρ(y)为基本的单位区间单调(BUM)函数,满足以下三个条件:ρ(0)=0;ρ(1)=1;若x>y,则ρ(x)≥ρ(y).
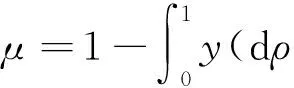
fρ([a,b])=μb+(1-μ)a
(2)
定义3[7]:令
(3)
则称εit是在第t时刻第i种单项预测方法基于COWA算子的区间预测的相对误差.
令
(4)
则称ait为在第t时刻第i种单项预测方法基于COWA算子的区间预测精度.显然,ait∈[0,1].
定义4[7]:在组合预测中,基于COWA算子的区间预测精度ait可以作为单项预测值xit的诱导变量.此时,m种单项预测方法在第t时刻基于COWA算子的预测精度和对应的区间预测值构成了m个二维数组
称
(5)
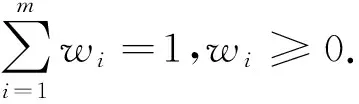
该算子可以视为COWA算子和IOWA算子的结合,先通过COWA算子将区间数转化为实数,再通过IOWA算子将转化后的实数进行集成.
定义5:Rm→R为m元函数,称
(6)
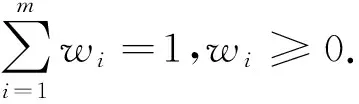
定义6[4]: 设A,B,C∈R(X)且映射Γ:R(X)×R(X)→[0,1]满足下列条件:
(1)Γ(A,B)=Γ(B,A);
(2)Γ(A,A)=1,Γ(A,Φ)=0;
(3)0≤Γ(A,B)≤1;
(4)若对于∀x∈X,A(x)≤B(x)≤C(x),有Γ(A,C)≤Γ(A,B)且Γ(A,C)≤Γ(B,C).
则称Γ为R(X)上的贴近度函数,而Γ(A,B)表示A与B的贴近度.
定义7[4]:当有向量X=(x1,x2,…,xt),A,B∈R(X),可定义最大—最小贴近度Γ:
(7)
式中:∨、∧分别表示取大、取小运算.
定义8:令yt=COWA(xt),yit=COWA(xit),ya-index(it)=COWA(xa-index(it)),

为区间实际值序列与组合预测方法下的基于广义ICOWA算子的预测值序列λ次幂之间的最大—最小贴近度.
贴近度越大,说明两个变量之间的关系越接近.若以最大—最小贴近度作为衡量预测方法有效性的准则时,我们自然希望这个数值越大越好.当贴近度趋近于1时,这就说明预测的结果更为合理有效.
(8)
2 基于广义ICOWA算子的预测模型的构建
以最大—最小贴近度为最优准则的基于广义ICOWA算子的区间组合预测模型如(9)所示:
(9)
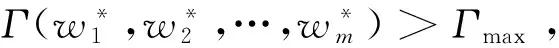
定义11[4]:若某种单项预测方法在组合预测模型中最优的权重系数中为零, 则称该单项预测方法为冗余预测方法.也就是说,若某种单项预测方法被纳入组合预测模型时,不能增加该模型的最大—最小贴近度,表明该种单项预测方法只提供冗余信息,不能提高预测的有效性.
3 实际应用
为检验提出的以最大-最小贴近度为最优准则的基于广义ICOWA算子的区间组合预测模型的有效性,下面进行实例分析.为检验预测结果的准确程度,建立包含预测误差平方和(SSE)、均方误差(MSE)、均方百分比误差(MSPE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)等指标的预测精度评价体系来比较不同方法下预测误差的大小.相应的计算公式如(10)所示:
(10)
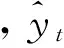
所采取的数据来源于参考文献[8].实际区间数xt和三组单项预测方法下预测区间数x1t、x2t、x3t见表1.

表1 实际区间数和三组单项预测方法下预测区间数
令BUM函数ρ(y)=y,则态度参数μ=0.5.说明此时决策者的风险态度是中性的.在这种风险态度下,表1中不确定的区间数经由COWA算子转化为确定的实数,并计算出相应的预测精度ait,见表2.
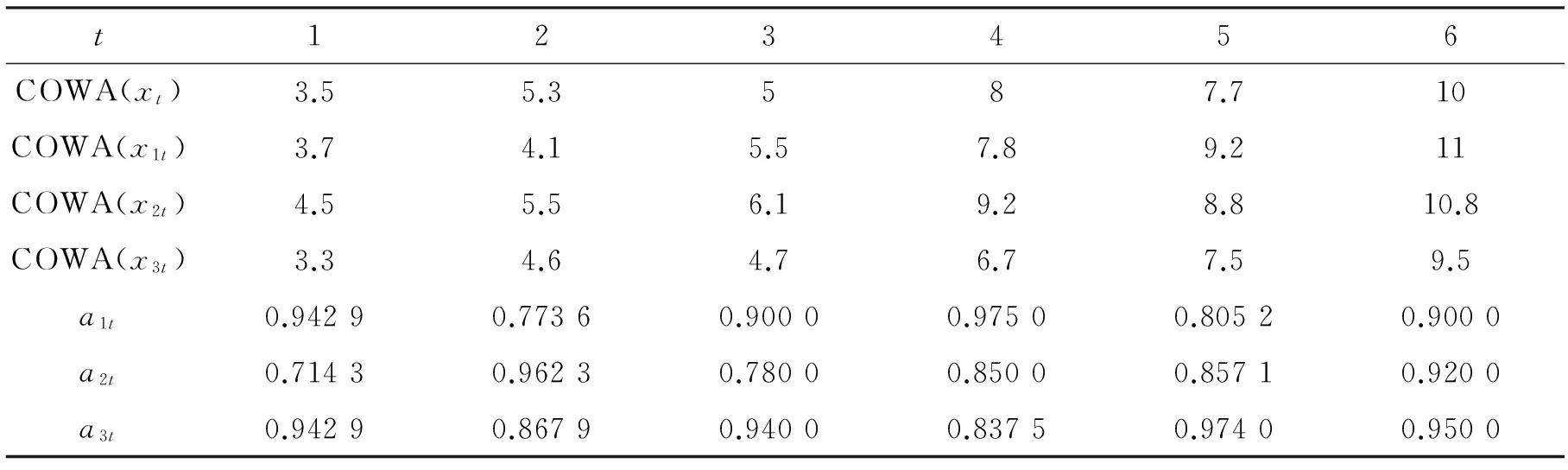
表2 μ=0.5时各项区间数经COWA算子转化的实数值和相应的预测精度
由ait作为诱导值产生新的实数序列COWA(xa-index(it)),列于表3中,见表3.

表3 由ait作为诱导值产生的实数序列COWA(xa-index(it))
对于t=1时,a1t=a3t,说明第1种和第3种单项预测方法在第1时刻的预测精度相同.对于每一个时刻,预测精度最高的单项预测方法赋予权重w1,预测精度较高的单项预测方法赋予权重w2,预测精度最低的单项预测方法赋予权重w3.
将以上求得的数据代入本文提出的基于最大-最小贴近度的广义ICOWA算子的区间组合预测模型,λ分别取值-1、1、5和趋近于0,通过MATLAB软件求得该模型的最优权重系数W=(w1,w2,w3),见表4.

表4 不同λ值下的最优权重系数
从中发现,当λ=-1时,权重系数w3取值为0,说明在每个时刻预测精度最差的某种预测结果在组合预测中提供的是冗余信息.
将预测精度评价体系中的五种误差指标应用于三种单项预测方法和本文提出的不同λ值下的区间组合预测方法,可以得到表5的误差序列数据,见表5.同时将不同方法下的最优贴近度位于最后一列,作为评价本文提出的组合预测模型是否为优性组合预测的标准.
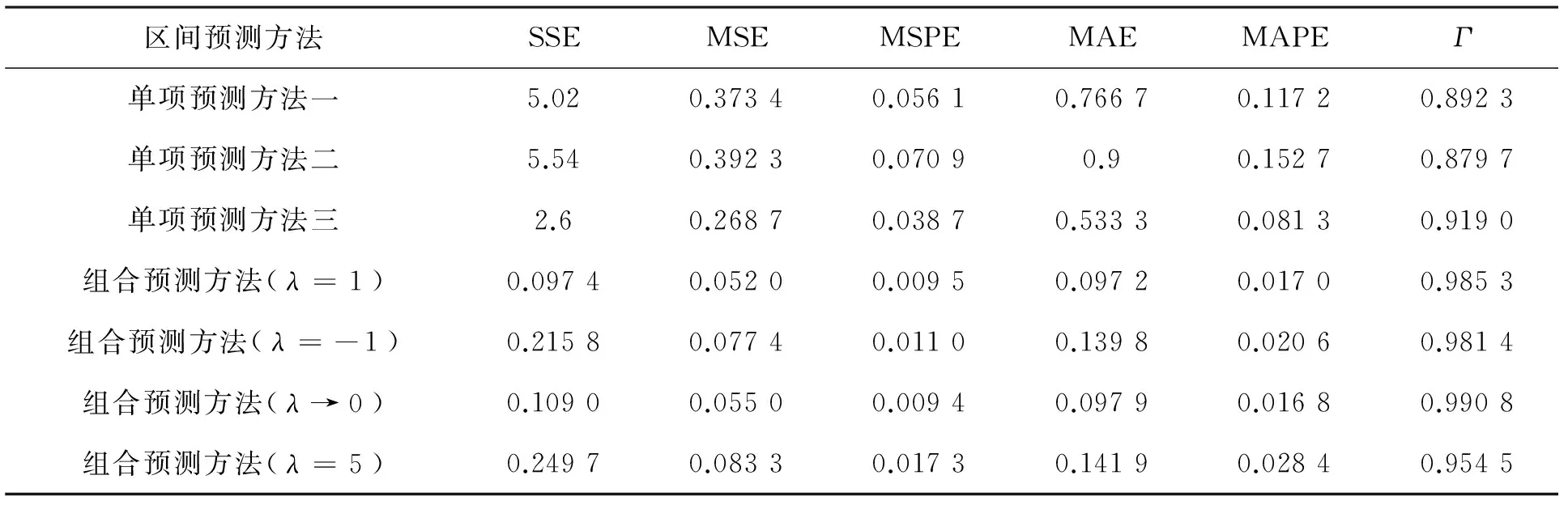
表5 各种区间预测方法下的各项误差和最大-最小贴近度
同时运用MATLAB软件编程,对本文提出的组合预测模型中λ值进行灵敏度分析,分别得到最大-最小贴近度和五类误差指标随λ值的变化而变化的趋势图,如图1与图2所示.其中λ值的取值范围为[-5,5].
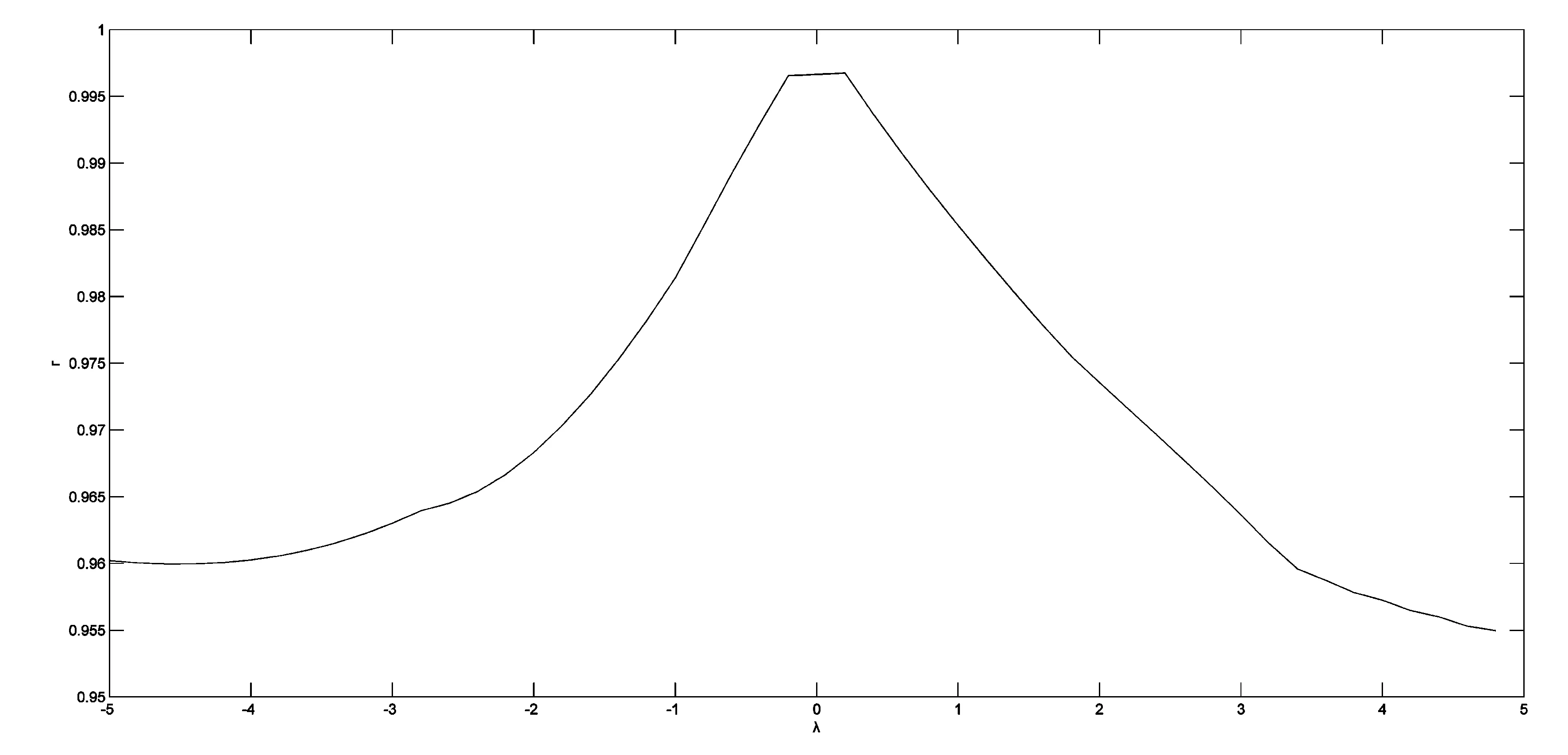
图1 最大-最小贴近度Γ的趋势变化图
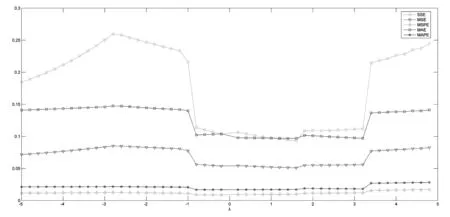
图2 五类误差指标的趋势变化图
由图1可知,随着λ值的变化,最大-最小贴近度呈现出先逐渐上升至极值点再逐渐下降的趋势,变化范围为(0.95,1),并且在λ→0时取得极大值.由图2可知,五类误差指标的变化趋势较为波折,有一定的相似性.它们在λ=-1时均出现一个较大幅度的下降,在区间(3,4)内都出现一个较大幅度的上涨.对于SSE来说,曲线的变动幅度较大,在[-5,-3]和[3,5]时处于上升阶段,不过取值始终低于0.3.而不管λ值如何变化,MAE和MSE的取值始终低于0.15和0.1;MAPE和MSPE的取值范围均小于0.05,变化趋势不明显.
当λ=1时,广义ICOWA算子就是常见的ICOWA算子;当λ=-1时,广义ICOWA算子转化成诱导连续区间有序加权调和平均算子,简称ICOWHA算子;当λ→0时,广义ICOWA算子转化成诱导连续区间有序加权几何平均算子,简称ICOWGA算子.从表5和图1、图2可以看出,无论是基于ICOWA算子、ICOWGA算子、ICOWHA算子或者其他的变化形式(比如λ=5),以最大—最小贴近度为最优准则的区间组合预测模型的各项预测误差均远低于三种单项预测模型的预测误差,这表明本文提出的区间组合预测模型能够有效提高预测精度.同时最大-最小贴近度Γ却都高于各单项预测方法的贴近度,说明最优组合预测模型是优性组合预测.因而该种模型是一种新的有效的区间组合预测方法.
4 结束语
本文首先通过COWA算子将区间数转化为确定的实数,再与IOWA算子结合并加以扩展,提出了广义ICOWA算子.其次引入贴近度的概念并经过取大取小运算,得到最大-最小贴近度的定义.建立以最大-最小贴近度为最优准则的广义ICOWA算子的组合预测模型,给出优性区间组合预测、非劣性区间组合预测、劣性区间组合预测、冗余方法和冗余度等概念,并针对该模型建立了评价体系,最后通过实例分析,该模型能有效提高结果的预测精度,是一种合理有效的区间组合预测方法.
[1]BatesJ-M,GrangerCWJ.Thecombinationofforecasts[J].JournaloftheOperationalResearchSociety, 1969, 20(4): 451-468. [2]汪新凡, 杨小娟. 基于联系数贴近度的区间数多属性决策方法[J]. 数学的实践与认识, 2008, 38(3):16-22.
[3]杨春玲, 张传芳, 许文翠. 基于区间数贴近度的不确定多属性决策模型[J]. 数学的实践与认识, 2010, 40(21):148-154.
[4]袁宏俊, 杨桂元. 基于最大-最小贴近度的最优组合预测模型[J]. 运筹与管理, 2010, 19(2):116-122.
[5]YagerRR.OWAaggregationoveracontinuousintervalargumentwithapplicationstodecisionmaking[J].IEEETransactionsonSystems,Man,andCybernetics,PartB(Cybernetics), 2004, 34(5):1952-1963. [6]YagerRR.GeneralizedOWAaggregationoperators[J].FuzzyOptimizationandDecisionMaking, 2004, 3(1):93-107.
[7]金飞飞, 李捷, 陈华友, 等. 基于连续有序加权平均算子的区间组合预测[J]. 武汉理工大学学报: 信息与管理工程版, 2013, 35(5):668-672.
[8]徐惠莉, 吴柏林, 江韶珊. 区间时间序列预测准确度探讨[J]. 数量经济技术经济研究, 2008, 25(1):133-140.
The Interval Combined Forecasting Model Based on Generalized ICOWA Operator and Maximum-minimum Approximation
PAN Rui, YUAN Hong-jun
(Institute of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu Anhui 233000, China)
In this paper, the maximum-minimum approximation and the generalized ICOWA operator are combined to predict the interval number and establish a new interval combined forecasting model. At the same time, this paper proposes the concepts of optimal interval combined forecasting, non-inferior interval combined forecasting, inferior interval combined forecasting, redundant method and redundancy rate, and then establishes an evaluation system on the model. Finally, with an example calculation, the paper concludes the interval combined forecasting is reasonable and effective.
maximum-minimum approximation; generalized ICOWA operator; interval combined forecasting; evaluation system
1673-2103(2017)02-0012-07
2017-03-26
国家社科基金青年项目(13CTJ006);安徽财经大学研究生科研创新基金资助项目(ACYC2015096)
潘瑞(1993-),女,安徽安庆人,在读硕士研究生,研究方向:经济统计.
袁宏俊(1978-),男,安徽庐江人,副教授,硕士,硕士生导师,研究方向:预测与决策分析.
O212.1
A
