Abrahamson相干模型对核电站构筑物埋置地下部位抗震响应的影响
2017-05-16徐征宇李忠诚
徐征宇,李忠诚
(深圳中广核工程设计有限公司,上海200241)
Abrahamson相干模型对核电站构筑物埋置地下部位抗震响应的影响
徐征宇,李忠诚
(深圳中广核工程设计有限公司,上海200241)
本文采用Abrahamson的空间相干性模型,并考虑基础埋置效应,针对硬岩、软土厂址对核电站构筑物开展空间相干性地震反应谱分析,评估其非一致性对于埋置部位的地震响应谱影响情况,并得出对于低频区段地面的空间非一致性影响反应谱程度与埋置面接近;而高频区段地面的空间非一致性影响反应谱程度比埋置面要大的结论。
空间相干一致性;埋置效应;非一致性;楼面反应谱
地震运动是复杂的空间运动过程,在传统的抗震设计上更多地关注时变效应而对空间变化效应考虑较少。经过研究表明,由于地震波在传播过程中由于局部波的散射和行波效应等,使得地震动在空间分布上具有比较明显的差异性,而这种地震动的非一致性对于结构本身的响应会产生较大的影响。
1970年以来,国内外很多学者和研究机构均提出过不同相干函数模型,1975年Matsushima把地面各点运动看作具有相同自功率谱密度函数的平稳随机过程. 提出了仅与距离相关的相干函数[1];1980年Hindy和Novak提出了互功率谱密度函数与距离和频率相关的相干函数[2];1986年Luco和Wong提出经典频率、距离和剪切波速等相关的相干函数模型,并应用于CLASSI软件[3];2005—2007年Abrahamson基于密集台阵测得的数据拟合了软土和硬岩的相干函数模型[4-6],并应用于SASSI软件。
本文是基于Abrahamson的相干函数模型,考虑非一致性的地震输入,选取硬岩和软土两种不同的场地条件,建立土与结构相互作用(SSI)的分析模型,通过比较一致性和非一致性相干模型输入对于核电站构筑物埋置地下部位响应的影响,为核电站项目地震分析和安全评价提供参考和建议。
1 空间相干性理论原理
1.1 空间相干性函数
对于位于j点和k点的平稳地震运动aj(t),ak(t),它们之间的相干函数Γj,k如下:
(1)
式中:Sj,k表示地震动之间的互功率谱密度函数,Sj,j和Sk,k表示地震动的自功率谱密度函数。同样相干函数Γj,k也可以用下式来表示:
Γj,k(ω)=|Γj,k(ω)|eiθj,k(ω)
(2)
式中:∣Γj,k(ω)∣表示空间相干效应,也称迟滞相干效应,eiθi,k(ω)表示相位差的行波效应。
1.2 空间相干性的反应谱计算理论[7]
(3)

(4)

(5)
式中:Sk(ω)是由于非一致性运动引起的随机空间运动的函数,在数学上是K点相对空间上随机变化的振幅的傅里叶复变换函数,可采用运动一致性的矩阵进行谱分解运算[8]求得,见下式:

(6)
ηθj(ω)=e(iθj)
(7)
式中:Φj,k(ω),λj(ω)分别是K点j阶特征向量和特征值,ηθj(ω)是j阶特征向量的相位部分。
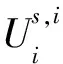
(8)
(9)
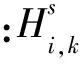
1.3 Abrahamson相干函数
在美国核管会NRC颁布的标准审查大纲SRP3.7[9]中规定在土结构相互作用的分析时要考虑地面运动的非一致性效应,并于2008年暂行管理导则(ISG-01)[10]中批准了Abrahamson基于硬岩的相干函数;而基于软土的相干函数则暂时仅用于科研及参考。
Abrahamson采用的分析数据是来源于加利福尼亚南部的密集台阵1990年至2006年间的287组实测地震数据,密集台阵的厂址地质条件是花岗石硬岩。对于每组记录,通过计算过滤窗后的加速度记录的平均傅里叶谱得到相干函数。由于Tanh-1|γ|曲线是近似正态分布的曲线,因此采用该函数来拟合相干函数。
Abrahamson基于硬岩以及软土的相干函数见图1和图2。

图1 Abrahamson硬岩水平相干性模型Fig.1 Abrahamson coherency models for hard rock
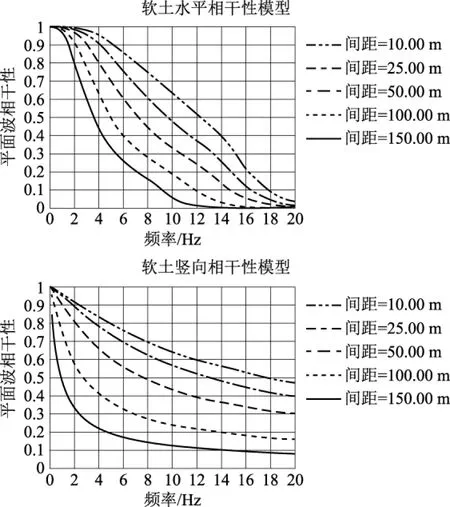
图2 Abrahamson软土水平相干性模型Fig.2 Abrahamson coherency model for soil
Abrahamson基于硬岩以及软土的相干函数公式如下:
(10)
式中:f表示频率(Hz)、ξ表示间距(m),其余参数见表1。
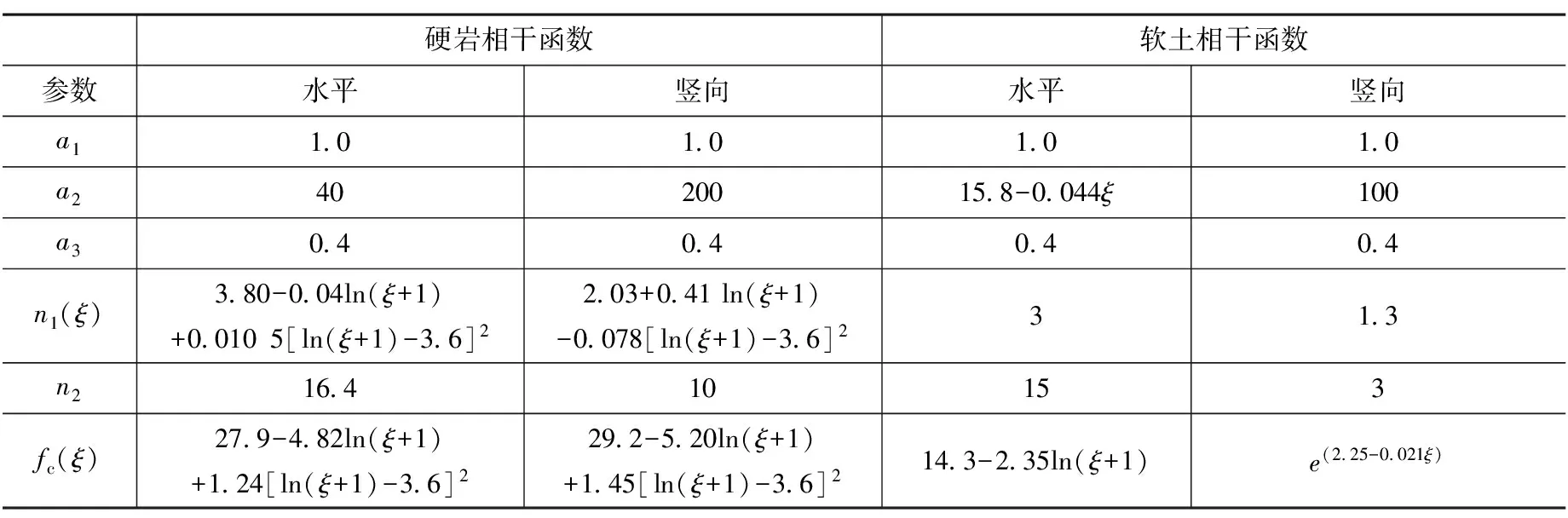
表1 Abrahamson的硬岩及软土相干函数模型的参数
2 核岛构筑物抗震响应分析
2.1 有限元模型
分析模型选取典型的第三代非能动压水堆堆型,见图3。ASB、CIS、SCV分别表示屏蔽厂房及核辅助厂房、安全壳厂房、钢安全壳的集中质量单元。模型的地下室底板和外墙采用实体单元,底板厚度为6ft,外墙厚度为3ft,埋置深度为39.5ft,地面标高为100ft。

图3 集中质量模型与地面自由场运动加速度时程Fig.3 Centralized mass model and ground free field motion acceleration time course
分析采用的土层条件分别为硬岩和软土两种厂址条件,详细参数见表2。分析采用3D单向地震分析,地面水平运动加速度时程选用非零均值的加速度时程,时间步长0.01s,共20s。输入的地面加速度时程求得的反应谱包络NRC的管理导则RG1.60[11]高频修正谱。
在计算硬岩、软土场地参数的空间相干性对埋置效应的影响时,选用的空间相干性模型是Abrahamson的硬岩相干模型;计算分析楼面反应谱的分析程序选用ACS-SASSI程序。
2.2 分析结果
基于硬岩和软土两种不同场地参数的楼面反应谱分析结果对比来看,总体而言,地面运动的非一致性使得埋置地面以下的部位的楼面反应谱值相比不考虑空间相干非一致性,在高频区域(10~20Hz)有较为明显的降低,尤其是硬岩厂址。
从图4~图5来看,地面运动非一致性对于硬岩厂址高频区埋置部位的相干影响程度要比在软土厂址的相干影响程度要大;在低频区相干影响不明显。
图6是取地面运动非一致性降低幅度为纵坐标。从图上来看,对于低频区域(硬岩厂址:小于5Hz;软土场地条件:小于1Hz),空间相干性影响对于埋置深度影响不大,即地面的空间非一致性影响反应谱程度与埋置面接近。对于高频区(10~20Hz),空间相干影响程度大体随着埋置深度加深而减小,意味着地面的空间非一致性影响反应谱程度比埋置面要大。
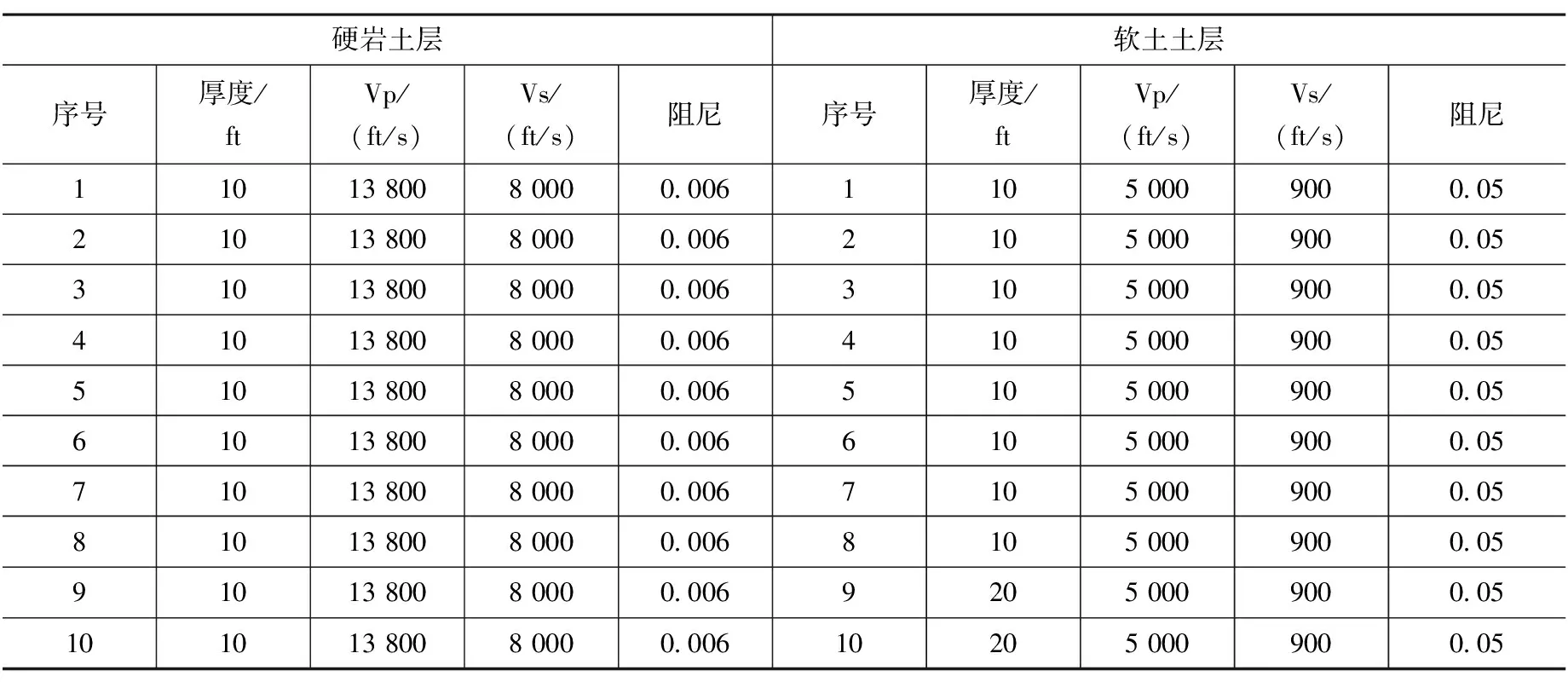
表2 土层剖面参数

图4 硬岩厂址埋置地下位置的x向楼面反应谱Fig.4 x-direction floor response spectra for embedded part on hard rock site

图5 软土厂址埋置地下部位的x向楼面反应谱Fig.5 x-direction floor response spectra for embedded part on soft soil site

图6 硬岩和软土厂址土层参数的相干性影响大小比较Fig.6 Comparison of the impact of incoherency for hard rock and soft soil site
3 结论
本文采用Abrahamson的空间相干性模型,分别于硬岩、软土两种不同的场地条件,针对核电站构筑物并考虑埋置效应开展空间相干性对于地震楼面反应谱的影响分析,得出结论如下:
(1) 地面运动非一致性使得埋置地下部位的楼面反应谱幅值在高频区域有较为明显的降低。
(2) 对于埋置于地下的部位,在高频区段(10~20Hz),地面运动非一致性对岩性厂址的楼面反应谱的影响程度要比在土性厂址的影响程度要大;
(3) 对于低频区域,地面的空间非一致性影响楼面反应谱程度与埋置面接近。对于高频区段,地面的空间非一致性影响反应谱程度比埋置面要大。
[1] Y.Matsttshima, Spectra of spatially variant ground motion and associated transfer functions of soil foundation system,1975, 4th Japan Earthquake engineering symposium.
[2] A.Hindy, M.Novak,Pipeline response to random ground motion,1980,ASCE 106, 339-360.
[3] Luco, J.E.,H.L. Wong. Response of a Rigid Foundation Subjected to a Spatially Random Ground Motion, Earthquake Engineering and Structural Dynamics, 1986, Vol.14, pp.891-908.
[4] Abrahamson, N., Spatial Coherency for Soil-Structure Interaction. 2005, EPRI, December. Technical Update Report 1012968.
[5] Abrahamson, N., Program on Technology Innovation: Spatial Coherency for Soil-Structure Interaction. 2006, EPRI, December, Report 1014101.
[6] Abrahamson, N., Hard Rock Coherency Functions Based on the Pinyon Flat Data, 2007,April 2.
[7] Dan M. Ghiocela, Dali Lib, Keith Cooglerb, Leonardo Tunon-Sanjur, “Seismic Motion Incoherency Effects for AP1000 Nuclear Island Complex” 20th International Conference on Structural Mechanics in Reactor Technology(SMiRT-20), August 9-14,2009,pp.1852
[8] Tseng, Lilhanand. Soil-Structure Interaction Analysis Incorporating Spatial Incoherence of Ground Motions,1997, EPRI, Palo Alto, CA, Report No. TR-102631 2225.
[9] U.S. Nuclear Regulatory Commission, Standard Review Plan, NUREG-0800, 2014.
[10] U.S. Nuclear Regulatory Commission, “Seismic Issues Associated with High Frequency Ground Motion in Design Certification and Combined License Applications”, ISG-01, 2008.
[11] U.S. Nuclear Regulatory Commission, Design Response Spectra for Seismic Design of Nuclear Power Plants. (RG1.60), Rev. 2, July 2014.
The Impact of the Abrahamson Spatial Coherency Models on the Seismic Response of the EmbeddedPart of Nuclear Island Structures
XU Zheng-yu,LI Zhong-cheng
(China Nuclear Power Design Co., Ltd., Shanghai 200241, China)
In this paper, the Abrahamson spatial coherence models, respectively of hard-rock site and soft-soil site, are used on seismic floor response spectrum analysis of the embedded part of nuclear power plant structures. Comparisons of impact results are shown and the impact of the incoherency on the embedded part in different frequency bands for seismic response spectra is evaluated, and it is concluded that the embedded incoherency is similar to the surface incoherency at low frequency and less than the surface incoherency at high frequency on seismic response for nuclear power plants.
Spatial coherency; Embedded effect; Incoherency; Floor response spectra
2016-06-4
徐征宇(1977—),男,上海人,高级工程师,硕士,现主要从事核岛结构厂房的抗震系统分析、流-固耦合分析,土-结构相互作用分析,屏蔽厂房抵抗大型商用飞机撞击分析等相关内容
TU311.3
A
0258-0918(2017)02-0176-06
