考虑地震动地形效应的边坡破坏概率——以金沙江下游新市镇附近边坡为例

刘爱娟，郑 路，刘铁新，李丽勤

(1. 四川大学水力学与山区河流开发保护国家重点实验室,水利水电学院，四川 成都 610065；2. 四川大学-香港理工大学灾后重建与管理学院，四川 成都 610207)

考虑地震动地形效应的边坡破坏概率
——以金沙江下游新市镇附近边坡为例

刘爱娟1，郑 路2，刘铁新1，李丽勤1

(1. 四川大学水力学与山区河流开发保护国家重点实验室,水利水电学院，四川 成都 610065；2. 四川大学-香港理工大学灾后重建与管理学院，四川 成都 610207)

边坡在地震作用下的破坏概率是地震边坡危险性评价的参数之一。在区域范围内计算地震边坡破坏概率一般采用实际地震滑坡和Newmark永久位移拟合得到的破坏概率公式进行计算。计算中所需的地震动峰值加速度数值大小受不规则地形的影响较大。为了较准确计算出区域地震边坡的破坏概率，本文利用公式分别计算了地震动峰值加速度地形效应系数和地震边坡滑坡概率，实现了地震动峰值加速度及滑坡概率的连续分布。在计算地表30 m平均剪切波速时，利用回归分析方法得出了Vs30与地形梯度G的连续性关系。这些方法充分考虑了地形在地震动峰值加速度中所起的作用，能够实现地震边坡破坏概率计算结果的连续性，如实反映了地震边坡破坏概率的实际状况，为更准确评价地震边坡滑坡危险性提供了新的思路。

地形效应；地震；边坡；破坏概率

0 引言

中国西南地区活动断层密布、山区面积广大，因而地震多发，并在震后诱发了大量滑坡、崩塌等地质灾害，例如2008年汶川地震就产生了大量的地质灾害[1]。从长期来看，大部分地区的边坡都处在较高的地震危险性中。目前主要通过计算边坡在地震时的永久位移和破坏概率对区域边坡未来在地震作用下的危险性进行判断。

为了计算地震边坡破坏概率，Jibson[2]利用1994年美国北岭地震时划分的滑坡分布图与同样区域的永久位移分布图进行对比分析，以Weibull曲线为基本形式拟合了地震滑坡发生概率与永久位移的关系并在2000年[3]增加数据集进行了改进。Rodríguez-Peces[4]利用2011年意大利Lorca地震数据拟合出同样形式的滑坡概率方程。

Jibson[5]和Papathanassiou[6]分别应用Jibson 2000年的改进公式进行了美国安克雷奇地区和希腊Skolis山的地震边坡破坏概率分析。

Jibson和Rodríguez-Peces所拟合的地震边坡破坏概率公式主要表达破坏概率和Newmark永久位移之间的关系。对于区域范围地震边坡Newmark永久位移的计算，一般需要地震动基本参数如峰值加速度和边坡物理力学参数两方面的信息。利用地震动衰减关系可以得出研究区域的基岩峰值加速度。从原理上讲，根据地震动衰减关系建立起的峰值加速度是地震波传至基岩时呈现出的大小。然而，由于实际地形的影响，不同的地形条件对地震动峰值加速度起着不同程度的放大或缩小效应，这种效应致使同一边坡上的峰值加速度相差很大。如自贡西山公园设置的监测仪器显示，在2008年汶川地震时，山体各处峰值加速度均表现出不同程度的放大作用[7-8]，大型振动台试验研究成果也表明了同样的结果[9-10]。在复杂的山地地形区，不同地形对峰值加速度改变量能够达到50%。

对地震边坡地形效应的研究主要集中在三个方面。

(1) 实际监测。建设强震动地形观测台阵系统研究地形对地震动参数的影响。

(2) 振动台试验。利用实验室振动台试验进行地震边坡的物理模拟寻找地震动参数随震动强度和坡形的变化规律。

(3) 数值模拟。利用计算机数值模拟技术寻找地震动参数随地震动强度和坡形的变化规律[11-13]。

目前，以上三种研究方法均有一定的进展，但由于是对单体边坡加速度的监测研究，实际监测和振动台试验两种方法还难以得出通用的地形效应系数。数值模拟方法对边坡进行了大量简化，能够在较短的时间内得出不同工况下的加速度放大或缩小数值，但仍存在与实际地震边坡工况相差较大的缺点。对于区域性地震边坡峰值加速度的计算，数值模拟方法可以提供通用性地形效应系数以对基岩峰值加速度进行调整。

本文结合以上研究成果，以金沙江下游新市镇附近部分河流岸坡为研究区域，通过回归分析得出Vs30与地形梯度的连续性关系，引入地形效应系数公式和地震滑坡概率公式分别计算了具有连续分布形式的地形效应系数和地震滑坡概率。

1 研究区概况

金沙江下游溪洛渡至新市镇段，猰子坝断层呈近似与该段河道平行的方向延展，并两次横穿金沙江，是该区域最大的一条逆断层，倾角为70°～80°。该断层第四纪以来有过活动，隶属于荥经-马边-盐津断裂带。猰子坝断层区域附近曾发生两次7级以上地震即1974年断层南端的永善-大关7.1级地震和1216年断层附近的马湖7级地震[14-16]。据中国地震台网站数据，从2012年6月至2016年6月，猰子坝断层附近发生地震4次。虽然该区域附近还有中村断层和关村断层，这两条断层的活动性比猰子坝断层弱，没有表现出明显的活动性。

以上的地震记录均表明，猰子坝断层是一条活动性断层，南端和北端均发生过地震并且呈现出单次中强地震的明显特点，足以证明猰子坝断层仍处于活跃期。所以，鉴于该断层的特殊位置和频繁的活动性，有必要对其进行地震活动性分析并着重对其附近的金沙江岸坡进行地震危险性评价，研究区位置见图1。

图1 研究区位置图Fig.1 Location of the study area

2 基岩地震动峰值加速度分布

2.1 震源位置与最大震级

地震动预测方程需要确定单条断层上的震源位置和可能发生的最大震级。

对于中小地震，震源可以看做点源；对于震级较大的地震，震源的位置可以看做分布于整条断层上的线源。无论是点源还是线源，震源位置和震中距对于边坡的破坏作用都非常重要。从汶川地震滑坡分布相关文献[17-18]的统计分析可知，地震地质灾害在断裂带两侧呈现出明显的条带状分布，这种现象在震级较大的地震中尤为明显。

已知断层长度估算可能产生的最大震级时，采用震级与活断层预期断裂长度关系式与历史最大地震相结合进行确定。根据最新探查信息[19]，猰子坝断层长度为50 km，董瑞树[20]指出断层平均长度为50 km即可产生7.0级地震。本文采用的潜在最大震级与断裂长度关系式来源于三处文献[21]、[22]和[23]，公式和计算出的潜在最大震级见表1，其中Wells公式中的震级为矩震级，本文依照文献[24]中矩震级与面波震级的关系进行了换算(表1)。

表1 猰子坝断层潜在最大震级

通过以上经验公式计算并结合猰子坝断层附近历史最大地震记录，即1216年的7级马湖地震和猰子坝断层南端1974年7.1级永善-大关地震，将猰子坝断层可能诱发的最大震级定为7.3级，震源位置设置在整条断层上。

2.2 地震动预测方程

由于本文研究区位置处于川滇两省交界的金沙江附近，文献[25]中用于统计地震动衰减关系的数据资料来源于整个川滇地区，符合研究区域的地理位置。所以，利用该文献中的地震动衰减关系公式(1)计算研究区基岩峰值加速度PGA。

lg(PGA)=3.569+0.117M+(0.14M-2.274)

lg(R+0.996e0.375M)

(1)

以7.3级作为猰子坝断层潜在最大震级计算出的基岩PGA分布图见图2。

图2 基岩PGA分布图Fig.2 Bedrock PGA distribution

3 PGA地形效应

3.1 计算方法

目前进行地震动地形效应研究的三种方法虽然有了一定数量的研究成果，但能够适用于各种边坡的通用放大系数还很缺乏。Bouchovalas[11]利用数值模拟的方法分析了大量地形条件对地震动参数的影响并总结出了一定规律，该规律以地形放大系数为参数表达为式(2)。

(2)

该模型以竖直传播的SV波为入射波，材料为均值土或岩石环境，模拟条件为H/λ>0.16并且坡角大于7°。依照此式对地震动峰值加速度进行调整，可以在一定程度上体现山体地形的影响程度。

3.2 参数

公式(2)中的参数分别介绍如下：H为研究区域的边坡高度，即边坡相对高程，可由地理信息处理软件中的水文分析工具计算得出；I为边坡几何参数，计算方法为坡角除以90°，即I=α/90°，α=10°～90°；ξ为地基材料阻尼比，结合岩石和土的常用数据，可取ξ=0.05；λ为地震波长，由公式λ=V×T计算得出，计算过程中需要地震波速V和周期T，在无地震波实测资料的情况下可取地表以下30 m深度平均剪切波速Vs30作为地震波速。对于周期T，根据中国地震动反应谱特征周期分布图，研究区所处的金沙江岸坡反应谱特征周期为0.40 s，可作为本次计算中的周期T。

Vs30值与岩土的类别有关，在区域范围内很难实现通过大量实测工作得到该值。地形起伏变化能够体现近地表地层岩土性质的差别，如高陡的山地表明存在岩石或较硬土，平坦的平原与盆地表明分布有较软土层。许多研究也发现：Vs30与地形梯度、地貌及高程具有较好的相关性[26-28]。为了得到缺少实测数据区域的Vs30值，Wald和Allen通过统计地形梯度G与Vs30之间的相关性，提出利用场地地形梯度计算Vs30的方法并在2009年进行了修正[27-28]，表2所示为地形梯度G和Vs30的对应关系。

表2 地形梯度G与Vs30关系表

从表2中可以看出，Wald并未直接给出平均剪切波速大于760 m/s和小于180 m/s的地形梯度与Vs30的对应关系。为了解决这一问题并作出连续的Vs30分布图，本文对表2中的地形梯度G与Vs30分别做一次(式①)和二次(式②)回归分析。从回归曲线的分布形状和判定系数R2均可看出两种回归关系式在常用的取值范围内均可满足使用要求(图3)。

图3 地形梯度G与Vs30回归曲线及方程Fig.3 Regression curves and equations of G and Vs30

利用式①和式②两种回归方程式分别计算Vs30可以发现：由于一次直线关系的原因，式①得出的Vs30结果会出现合理的下限、不合理的上限；由于二次曲线的原因，式②得出的Vs30结果会出现合理的上限、不合理的下限。所以分别取式①结果的下限和式②结果的上限作为Vs30的取值界限。此外为了消除单条曲线的数据单向影响，再对两种数据结果取平均值即可得到最终的Vs30值。研究区地形梯度见图4，计算得的Vs30分布见图5。

图4 研究区地形梯度分布图Fig.4 Topography gradient of the study area

图5 研究区Vs30分布图Fig.5 Vs30 of the study area

3.3 计算地形效应系数

根据以上定义及计算出的各参数，利用公式(2)计算所得的地形效应放大系数见图6，系数分布范围为1～1.453 35，处于可接受的合理范围。从图中系数的分布特征也可以看出，较大的系数基本上分布于海拔较高的部位，符合高山区地形效应更加明显的特征。

图6 研究区地形效应系数分布图Fig.6 Topography effect coefficients of the study area

将研究区依据地震动衰减方程得出的基岩PGA分布图2与地形效应系数图6相乘可得到经过地形效应调整之后的PGA分布见图7。

对比分析调整前后的研究区PGA分布图2和图7，可以明显看到地形效应的放大作用，即峰值加速度高值区域分布变广，且随着地形变化分布更不规则。不规则的程度越大，说明调整结果具有更深的精细程度。

图7 地形效应调整后PGA分布图Fig.7 PGA after adjustment of topography effects

4 地震作用下边坡破坏概率计算

4.1 基础数据

计算临界加速度ac时，选取Jibson[3]给出的计算方法，暂不考虑地震时水的作用，修改得到计算临界加速度ac的计算公式为：

(3)式中：c——粘聚力/kPa；γ——重度/(kN/m3)；α——坡角/(°)；φ——摩擦角/(°)；t——滑块厚度/m；g——重力加速度/(m/s2)。

所需的工程地质岩组及岩土体参数根据1∶20万地质图地层岩性归纳为五类，岩组分类及参数见表3和图8。研究区的坡度数据以数字高程模型DEM为基础通过地理信息软件的空间分析功能实现。

表3 岩组分类及参数

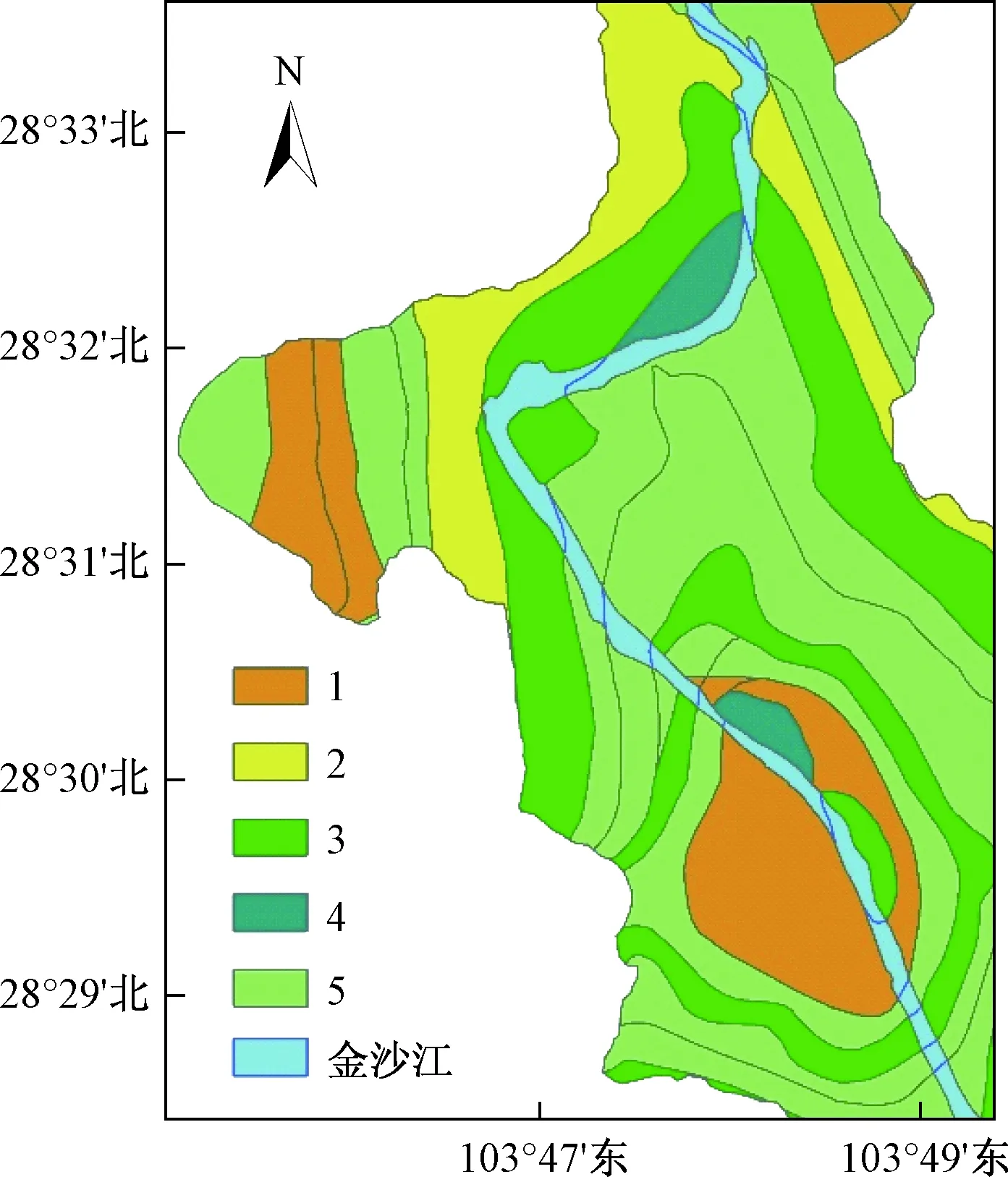
图8 研究区岩组分布Fig.8 Rock groups of the study area

在利用Newmark永久位移法判断地震边坡危险性时，通常认为该理论适用于浅层滑坡而不适用于受深部结构面控制的深层滑坡。所以，本文利用研究区附近区域岩体风化和卸荷深度数据并参考相关文献的取值范例确定各类地层的滑块厚度。研究区地层与上游溪洛渡处类似，可以溪洛渡水电站坝址处的风化卸荷深度作为滑块厚度取值参考。根据已有地质报告研究成果[29]，强卸荷带深度在不同的高程处也不同(表4)。

表4 溪洛渡强卸荷带下限(单位：m)

研究区高程范围为305～1 725 m，陡壁较多。利用表4中的数据并参考相关文献[30-31]的厚度取值，取滑块厚度t=3 m。计算出的研究区边坡临界加速度见图9。

图9 研究区临界加速度Fig.9 Critical acceleration of the study area

4.2 永久位移预测模型

本文研究区位于中国西南地区，为了更适合该区域的实际地质构造条件，本文采取文献[32]中利用汶川地震主震强震动记录回归得到的四川及其邻近省份山区的边坡永久位移预测模型如式(4)。

(4)

式中：DN——永久位移/cm；ac——临界加速度。

4.3 计算永久位移

根据以上数据及永久位移预测模型公式(4)，利用地理信息软件的地图代数功能计算出猰子坝断层在震级为7.3级时的边坡永久位移分布图(图10)。从图10可以看出，位移较大处基本分布在猰子坝断层两侧，基本沿断层呈条带状分布的震后地质灾害规律，但局部距离断层稍远处也有较大位移分布，这和该区域的岩性特征有较大关系。在实际应用中，可以对永久位移值较大部位的边坡加强观测与防护。

图10 研究区永久位移Fig.10 Permanent displacement of the study area

4.4 地震作用下边坡破坏概率计算

Jibson[3]的破坏概率公式更适用于山区，而Rodríguez-Pecesis[4]破坏概率公式的数据来自于西班牙洛尔卡盆地。由于本文研究区位于中国西南地区的高山峡谷地区，从地形上更符合Jibson概率公式的适用范围，所以选用公式(5)用于本文研究区的地震边坡破坏概率计算。破坏概率计算结果见图11。

(5)

图11 研究区边坡破坏概率Fig.11 Slope failure probability of the study area

永久位移结果和地震边坡破坏概率结果呈现出相似的分布特征，都在猰子坝断层附近呈现出较高的数值。所以，两者都可以作为评判危险性高低的依据。由于破坏概率公式综合考虑了实际滑坡和Newmark永久位移，能在一定程度上反映地震边坡破坏的可能性。

5 结论与建议

边坡在地震时不同位置的峰值加速度相差非常大，在利用地震动衰减方程进行区域地震动峰值加速度计算时有必要考虑边坡的地形效应。目前对于边坡地形效应研究的三种技术手段，即实际监测、振动台试验和数值模拟中，实际监测和振动台试验能够得出单体边坡比较准确的地形效应成果，但难以形成通用的成果。本文利用已有文献中利用数值模拟成果计算研究区域的地形效应系数以及调整后的峰值加速度，取得了连续且合理的分布效果。这说明在目前利用实测手段还无法获得通用的地形效应系数时，可以加强利用数值模拟获取地形效应的研究，或者利用数值模拟与实测数据相结合进一步获取更加精确的地形效应成果。

计算区域地震边坡的破坏概率能够在地震前为人们提供目标区域和地点的地震危险性判断依据。目前有关地震边坡破坏概率计算的成果不多，尤其是对于区域地震边坡而言，仅有前述Jibson等人做出的Newmark永久位移与破坏概率的相关关系式。通过本文的计算，Newmark永久位移与破坏概率呈相似的分布形状。此外，不同区域内依据实际滑坡数据拟合的破坏概率公式具有不同的适用范围，在使用时应尽量使用适合于本地区的破坏概率公式。地震边坡破坏概率结果可以表征区域内破坏可能性的相对大小，但其概率值是否就能代表真实的滑坡破坏概率还需要更多实例验证。

[1] 王根龙，张军慧，刘红帅. 汶川地震北川县城地质灾害调查与初步分析[J]. 中国地质灾害与防治学报，2009,20(3):47-51. WANG Genlong, ZHANG Junhui, LIU Hongshuai. Investigation and preliminary analysis of geologic disasters in Beichuan county induced by Wenchuan Earthquake [J]. The Chinese Journal of Geological Hazard and Control, 2009, 20(3):47-51.

[2] Jibson R W, Harp E L, Michael J A. A method for producing digital probabilistic seismic landslide hazard maps: an example from the Los Angeles, California, area [J]. Open-File Report, 1998.

[3] Jibson R W, Harp E L, Michael J A. A method for producing digital probabilistic seismic landslide hazard maps [J]. Engineering Geology, 2000, 58(S3-4):271-289.

[4] Rodríguez-Peces M J, García-Mayordomo J, Azaón J M, Jabaloy A. GIS application for regional assessment of seismically induced slope failures in the Sierra Nevada Range, South Spain, along the Padul Fault[J]. Environmental Earth Sciences, 2014, 72:2423-2435.

[5] Jibson R W, Michael J A. Maps showing seismic landslide hazards in Anchorage, Alaska [J]. Center for Integrated Data Analytics Wisconsin Science Center, 2009(5).

[6] Papathanassiou G. Estimating slope failure potential in an earthquake prone area: a case study at Skolis Mountain, NW Peloponnesus, Greece [J]. Bulletin of Engineering Geology & the Environment, 2012, 71(1):187-194.

[7] 王伟, 刘必灯, 刘欣，等. 基于汶川MS8.0地震强震动记录的山体地形效应分析[J]. 地震学报，2015(3):452-462. WANG Wei, LIU Bideng, LIU Xin, et al. Analysis on the hill topography effect based on the strong ground motion records of Wenchuan Ms8.0 earthquake [J]. Acta Seismologica Sinica, 2015(3):452-462.

[8] 范刚, 刘飞成, 张建经, 等. 地形对地震动的影响规律研究[J]. 地震工程学报, 2014, 36(4):1039-1046. FAN Gang, LIU Feicheng, ZHANG Jianjing, et al. Influence of topography on ground motion [J]. China Earthquake Engineering Journal, 2014, 36(4):1039-1046.

[9] 许强, 刘汉香, 邹威, 等. 斜坡加速度动力响应特性的大型振动台试验研究[J]. 岩石力学与工程学报, 2010, 29(12):2420-2428. XU Qiang, LIU Hanxiang, ZOU Wei, et al. Large-scale shaking table test study of acceleration dynamic responses characteristics of slopes [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12):2420-2428.

[10] 刘汉香, 许强, 周飞, 等. 含软弱夹层斜坡地震动力响应特性的振动台试验研究[J]. 岩石力学与工程学报, 2015, 34(5):994-1005. LIU Hanxiang, XU Qiang, ZHOU Fei, et al. Shaking table test for seismic responses of slopes with a weak interlayer [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(5):994-1005.

[11] Bouckovalas G D, Papadimitriou A G. Numerical evaluation of slope topography effects on seismic ground motion [J]. Soil Dynamics & Earthquake Engineering, 2005, 25(7-10):547-558.

[12] Ashford S A, Sitar N. Analysis of Topographic Amplification of Inclined Shear Waves in a Steep Coastal Bluff [J]. Bulletin of the Seismological Society of America, 1997, 87(3):692-700.

[13] Ashford S A, Sitar N, Lysmer J, Deng Nan. Topographic Effects on the Seismic Response of Steep Slopes[J]. Bulletin of the Seismological Society of America, 1997, 87(3):701-709.

[14] 韩德润. 马边—永善地震带构造形式及地震特征[J]. 地震地质, 1993(3):253-260. HAN Derun. The tectonic pattern and seismic characteristics of Mabian-Yongshan seismic zone [J]. Seismology and Geology, 1993(3):253-260.

[15] 彭云金, 吕加蓉. 荥经—马边—盐津断裂带新活动特征分析[J]. 四川地震, 2004(3):34-36. PENG Yunjin, LYU Jiarong. Consideration about the neo-active feature of Yingjing-Mabian-Yanjin fault zone [J]. Earthquake Research in Sichuan, 2004(3):34-36.

[16] 张世民, 聂高众, 刘旭东, 等. 荥经-马边-盐津逆冲构造带断裂运动组合及地震分段特征[J]. 地震地质, 2005, 27(2):221-233. ZHANG Shimin, NIE Gaozhong, LIU Xudong, et al. Kinematical and structural patterns of Yingjing-Mabian-Yanjin thrust fault zone, southeast of Tibetan plateau, and its segmentation from earthquakes [J]. Seismology and Geology, 2005, 27(2):221-233.

[17] 乔建平. 大地震诱发滑坡分布规律及危险性评价方法研究[M]. 北京：科学出版社，2014. QIAO Jianping. Earthquake-induced landslide distribution regularity and hazard assessment method [M]. Beijing：Science Press，2014.

[18] 许冲，徐锡伟，吴熙彦，等. 2008年汶川地震滑坡详细编目及其空间分布规律分析[J]. 工程地质学报，2013，21(1)：25-44. XU Chong, XU Xiwei, WU Xiyan, et al. Detailed catalog of landslides triggered by the 2008 Wenchuan earthquake and statistical analyses of the spatial distribution [J]. Journal of Engineering Geology, 2013, 21(1):25-44.

[19] 崔玉龙.猰子坝断层活动性及其滑坡灾害效应[D]. 成都：四川大学，2015. CUI Yulong. Activity of Yaziba fault and its disaster effects for landslides[D]. Chengdu: Sichuan University, 2015.

[20] 董瑞树，冉洪流，高铮. 中国大陆地震震级和地震活动断层长度的关系讨论[J].地震地质,1993(4)：395-400. DONG Ruishu，RAN Hongliu，GAO Zheng. The relationship between earthquake magnitude and length of active fault in China [J].Seismology and Geology，1993(4)：395-400.

[21] 陈达生. 地震引起的地表破裂长度与震级之间的经验关系[J].华北地震科学，1984，2(2)：26-32. CHEN Dasheng. Empirical relations between the length of the earthquake surface rupture and the magnitude [J].North China Earthquake Science，1984，2(2)：26-32.

[22] Slemmons D B. Determination of design earthquake for microzonation, 3rd International Earthquake Microzonation Conference Proceeding, 1982, Ⅰ of Ⅱ：119-130.

[23] Wells D L, Coppersmith K J. New empirical relationships among magnitude, rupture length, rupture width, rupture area and surface displacement[J]. Bull seism Soc Am, 1994, 84(4):974-1002.

[24] 沙海军, 吕悦军. 中国地震台网面波震级与矩震级的统计关系[J]. 国际地震动态, 2015(9):20-20. SHA Haijun, LYU Yuejun. Statistical relationship between surface wave magnitude and moment magnitude determined by China seismograph network [J]. Recent Developments in World Seismology, 2015(9):20-20.

[25] 王玉石，李小军，周正华. 川滇地区水平向强地震动衰减关系研究[J]. 地震学报，2013，35 (2)：238-249. WANG Yushi，LI Xiaojun，ZHOU Zhenghua. Research on attenuation relationships for horizontal strong ground motions in Sichuan-Yunnan region [J]. Acta Seismologica Sinica, 2013, 35 (2):238-249.

[26] Matsuoka M, Wakamatsu K, Fujimoto K, et al. Nationwide site amplification zoning using GIS-based Japan Engineering Geomorphologic Classification Map [J]. 2005.

[27] Wald D J, Allen T I. Topographic Slope as a Proxy for Seismic Site Conditions and Amplification. Bull of Seismological Society of America, 2007, 97:1379-1395.

[28] Allen T I, Wald D J. On the Use of High-Resolution Topographic Data as a Proxy for Seismic Site Conditions (Vs30). Bull of Seismological Society of America, 2009, 99:935-943.

[29] 成都勘测设计研究院. 溪洛渡水电站可行性研究报告[R].2002. Chengdu Engineering Corporation Limited. Feasible research report of Xiluodu Hydropower Station[R].2002.

[30] 葛华, 陈启国, 王德伟. 地震滑坡危险性评价及编图——以映秀震中区为例[J]. 中国地质, 2013, 40(2):644-652. GE Hua, CHEN Qiguo, WANG Dewei. The assessment and mapping of seismic landslide hazards: a case study of Yingxiu area, Sichuan province [J]. Geology in China, 2013，40(2):644-652.

[31] 王涛，吴树仁，石菊松，等. 基于简化Newmark位移模型的区域地震滑坡危险性快速评估——以汶川MS8.0级地震为例[J]. 工程地质学报, 2013, 21(1):236-236. WANG Tao, WU Shuren, SHI Jusong, et al. Case study on rapid assessment of regional seismic land-slide hazard based on simplified Newmark displacement model: Wenchuan Ms 8.0 earthquake [J]. Journal of Engineering Geology, 2013, 21(1):236-236.

[32] 徐光兴，姚令侃，李朝红，等. 基于汶川地震强震动记录的边坡永久位移预测模型[J]. 岩土工程学报，2012，34(6)：1131-1136. XU Guangxing，YAO Lingkan，LI Chaohong, et al. Predictive models for permanent displacement of slopes based on recorded strong-motion data of Wenchuan earthquake [J]. Chinese Journal of Geotechnical Engineering，2012，34(6)：1131-1136.

Seismic slope failure probability considering the topography effects —Case of slopes near Xinshi town alongside the lower Jinsha river

LIU Aijuan1,ZHENG Lu2,LIU Tiexin1,LI Liqin1

(1.StateKeyLaboratoryofHydraulicsandMountainRiverEngineering，CollegeofWaterResource&Hydropower，SichuanUniversity，Chengdu,Sichuan610065，China；2.SichuanUniversity-HongKongPolytechnicUniversityInstituteforDisasterManagementandReconstruction,Chengdu,Sichuan610207,China)

The failure probability of slope under earthquake is one of the parameters of seismic slope risk assessment. The failure probability formulas obtained by combining the actual seismic landslide and the Newmark permanent displacement are selected to calculated the failure probability generally. The peak ground acceleration required in the calculation is greatly influenced by the irregular topography. In order to calculate the failure probability of regional seismic slope more accurately, this study calculates the topography effect coefficients and the failure probability separately using formulas and achieves the continuous topography effect coefficients and failure probability. Continuous relations betweenVs30and topography gradientGare acquired by regression analysis for calculating the average shear wave 30 m below the earth surface. These methods take full account of the role of the terrain played in the peak acceleration of ground motion and the continuity of the calculated results of the seismic slope failure probability is realized. By means of this method, the actual condition of the slope failure probability is reflected, which provides a new idea for more accurate seismic slope risk assessment.

topography effects；earthquake；slope；failure probability

10.16031/j.cnki.issn.1003-8035.2017.01.02

2016-06-13;

2016-07-29

国家重点基础研究发展规划(973)项目(2015CB057903)；NSFC国际合作项目(41661134012)；国家自然科学基金项目(51509173)

刘爱娟(1980-)，女，河南民权人，博士研究生，主要从事地震地质灾害方面的研究工作。E-mail: liuaijuan333@126.com

郑 路(1982-)，男，副研究员，主要从事岩土工程和地质灾害减灾理论的教学及研究。E-mail: zhenglu@scu.edu.cn

P642

A

1003-8035(2017)01-0004-09