冲击波阵面几何扰动衰减特性及材料强度效应研究
2017-05-15马海霞马小娟孔歌星郝斌斌刘福生
马海霞, 马小娟, 孔歌星, 李 勇, 郝斌斌, 刘福生
(西南交通大学 材料先进技术教育部重点实验室 物理科学与技术学院, 四川 成都 610031)
冲击波阵面几何扰动衰减特性及材料强度效应研究
马海霞, 马小娟*, 孔歌星, 李 勇, 郝斌斌, 刘福生
(西南交通大学 材料先进技术教育部重点实验室 物理科学与技术学院, 四川 成都 610031)
非理想球面冲击波的几何整形问题是强冲击动力学研究的关键问题之一,因此研究冲击波阵面几何扰动的衰减特性与金属材料的动力学性质之间的关系成为冲击波物理研究领域的一个重要课题.利用二维有限差分方法数值再现飞片碰撞扰动实验,得到金属铝中冲击波振面扰动随传播距离演化的全过程.利用数值模拟发现金属铝的屈服强度对扰动衰减曲线上的2个特征点非常敏感,即零相位点和最大反向点,给出他们之间的定量关联.数值分析结果为飞片碰撞扰动方法研究材料的强度效应提供合理的理论支持,并提供一个研究材料强度效应的新思路.
强度效应; 冲击波振面扰动; 铝
在强冲击动力学过程中,保证金属飞层球面几何形状是实现球形内爆的关键,为此须要对驱动金属飞层的冲击波进行球面整形.在工程中,人们通常借助冲击加载介质对流场能量和动量的耗散机制,使非理想球面冲击波阵面上几何扰动经历一个震荡衰减过程,最终演变为近似球面冲击波.由此可见,冲击波阵面几何扰动的衰减特性研究[1]具有重要的应用背景.
在1965年,A. D. Sakharov等[2]采用化爆冲击加载技术产生具有近似正弦形几何扰动的非平面冲击波,利用波阵面扰动幅度的震荡衰减行为与金属黏性之间的关联性,提出一种评价冲击高压下金属等效黏性的实验方法.2005年,刘福生等[3-5]将该技术移植到二级轻气炮上,并发展了一套飞片加载产生冲击波的飞片碰撞扰动法,评估过金属铝和铁在兆巴压力下的等效剪切黏性行为.研究表明,冲击加载下金属材料的黏性系数的取值约103Pa·s.对于液态金属,其黏性行为取决于原子扩散引起的动量耗散机制,其黏性系数的分子动力学模拟结果仅为10-3~10-2Pa·s[6-8].2种物态下金属材料的黏性系数相差如此巨大,可能是由于固态金属的等效黏性含有材料强度效应的贡献.
在固体材料中,黏性和材料强度对冲击波阵面的扰动衰减行为均有显著影响,而且在远离熔化线的状态下材料强度对固体材料中冲击波阵面的演化行为起主导作用.本文以冲击压力30 GPa条件下的金属铝为例(在此冲击压力下金属铝并没有发生冲击熔化),对其强度效应进行研究.利用有限差分方法数值模拟冲击波振面扰动随传播距离的演化过程,分析铝的强度效应对演化特征的影响,为进一步利用飞片碰撞扰动法测量材料的强度效应奠定理论基础.
1 数值模拟
利用数值分析对飞片碰撞扰动法中金属铝被加载到30 GPa时,样品中扰动冲击波阵面演化的全过程进行模拟;数值模拟的网格设计和参考坐标系如图1所示.在x、z方向上设定格子数分别为8 000和2 000,计算的时间步长为2ps.假设飞片沿x轴正向运动,其速度大小由冲击压力计算得到.样品的碰撞表面设计成正弦形曲面,如图1,其形状用波长(λ)和幅度(h)描述,这样就可以在样品冲击波阵面上形成正弦形微小扰动.由于正弦函数具有周期性,因此在垂直于运动方向上设置周期性边界条件,而在流场的左右两端设置连续边界条件以避免波反射效应.飞片和样品均为金属铝.

计算中设定飞片处的压力值为30GPa,这一条件下铝的状态方程由其Hugoniot状态方程和Grüneisen状态方程决定.利用压力计算飞片流场的横向初始速度ux=3km/s,令其纵向初始速度为零.样品和飞片流场的初始密度ρ0均为2.704g/cm3,为保证介质流场的连续性,假设飞片与样品碰撞的间隙密度为10-6ρ0.样品流场的初始压力、内能和速度为零,流场中物理量满足Rankine-Hugoniot关系,并假定ργ=ρ0γ0(γ0=1.97).
整个弹塑性流场的运动满足质量、动量和能量守恒[9],其质量守恒方程为
(1)
动量守恒方程为
(2)
能量守恒方程为
(3)
其中,ρ为流场密度,ux、uz分别为x、z方向流场速度分量,τxx、τxz、τzz分别为应力分量.
流场演化过程中,偏应力τ满足如下关系

(4)
其中,e为偏应变,上面的点表示对时间的一阶导数;Y和G分别为屈服强度和剪切模量,模拟过程中屈服强度Y人为赋值,剪切模量G由D.J.Steinberg等[10]给出的本构方程计算得到

上述所有方程都采用C.H.Mader[11]的二维欧拉差分格式进行数值计算.
本文是利用波后流场演化特征研究材料的强度特性,故不特别关心波阵面厚度,因此在波阵面区域内仅采用人为黏性以抑制波阵面前沿处数值震荡,对其合理取值确保得到收敛的数值计算结果,因此假定冲击波阵面内无强度效应.波阵面前沿后方流场视为弹塑性介质,由材料的剪切模量和屈服强度决定.
2 计算结果
飞片以3km/s的速度沿x轴正向运动,与样品的正弦形扰动的“峰”部相撞,此刻在该撞击区域的飞片与样品中分别形成了沿x方向传播的反向而行的2列冲击波.当飞片与样品表面完全碰撞(即飞片与样品之间的间隙完全闭合)时,在飞片和样品中各形成一列具有完整近正弦形扰动图样的冲击波阵面,如图2所示.波阵面后方流场的压力分布完全由材料的高温高压物性决定,无法预先写出流场的解析表达式.此时样品中冲击波阵面扰动幅度称为初始扰动幅度a0,其大小可利用(7)式计算得到
(7)
其中D为样品中冲击波速度,可利用Rankine-Hugoniot关系计算得到.在随后的流场演化过程中,波阵面扰动幅度将不断减小到零,反相增大到最大值后继续震荡下去.其演化的具体特征是本文研究高温高压下金属铝强度效应的依据.在整个模拟过程中扰动波长λ保持不变.
在x-z平面内利用最大压力梯度捕获法[12]确定任意时刻冲击波阵面的形状及其位置,进而可以得到冲击波振面扰动幅度随传播距离的演化过程.通常这一过程利用冲击波阵面扰动幅度衰减曲线来描述,其横坐标为相对距离(即冲击波从初始时刻开始传播的距离x与正弦扰动波长λ的比值),纵坐标为相对幅度(即任意时刻的扰动幅度a与初始扰动幅度a0的比值).
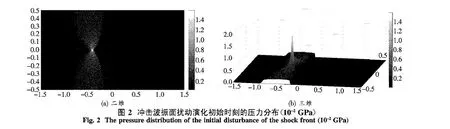

图3给出冲击压力30GPa条件下铝样品中冲击波阵面扰动幅度随其屈服强度变化的扰动衰减曲线.可以看出,不同强度条件下冲击波振面扰动的演化规律类似.从初始时刻开始,随着冲击波在铝样品中向右传播,其扰动幅度不断减小,并且降为零,此位置称之为零相位点(第一个相对幅度为零的点);之后反向幅度增大,达到反向最大值(这一值远小于初始扰动幅度),此位置称之为反向最大点(第一个反向幅度最大的点).随着冲击波在铝样品中继续传播,扰动幅度继续减小,扰动幅度第二次为零,如果系统能量足够大,还会正向增大,然后减小,一直震荡下去.根据图3中屈服强度在0~1.8GPa范围取值时各条冲击波阵面扰动幅度衰减曲线的变化情况,发现他们的零相位点和反向最大点的位置对屈服强度非常敏感.由此给出衰减曲线上的这2个特征点随屈服强度的变化规律,如图4和5所示.
零相位点的横坐标值表示冲击波振面扰动振幅为零时远离初始扰动位置处的相对距离,其值随屈服强度增大而非线性增大,如图4.当Y=0GPa时,零相位点的横坐标为0.68,随着屈服强度的增加,零相位点不断右移;当Y=1.8GPa时,零相位点的横坐标已经到达0.94.很显然在1.8GPa的范围内,屈服强度越大,冲击波扰动幅度衰减到零的速度越慢.


最大反向点的纵坐标揭示了第一个周期内冲击波振面扰动幅度的反向最大值.当Y=0GPa时,冲击波振面反向扰动相对幅度为0.26.屈服强度越大,反向扰动幅度越小,如图5所示.当Y=1.8GPa时,反向扰动相对幅度只有0.04.如果屈服强度再大些,冲击波振面扰动很可能无法回到零相位点.
3 结论
本文以30GPa条件下的金属铝为例,根据飞片碰撞扰动法的实验设计,利用有限差分方法数值模拟了样品铝中冲击波振面扰动随传播距离演化的全过程.决定金属铝强度特征的2个物理量中的剪切模量由Steinberg给出的本构方程确定,屈服强度人为赋值.结果发现:冲击波阵面扰动幅度衰减曲线上的2个特征点均对金属铝的屈服强度值非常敏感.在0~1.8GPa范围内,金属铝的屈服强度越大,零相位点越晚到达,反向幅度越小.如果能利用飞片碰撞扰动实验法测量出材料中冲击波振面扰动的演化过程,结合本文的数值分析,就可以定量分析材料的屈服强度.因此,本文为进一步利用飞片碰撞扰动法分析材料的强度效应提供了有效的理论支持.
[1] 赵彦生,魏英. 研究多相状态方程的冲击压缩技术[J]. 国外核武器研究,2004(4):109-115.
[2] SAKHAROV A D, ZAIDEL R M, MINEEV V N, et al. Experimental investigation of the stability of shock waves and the mechanical properties of substance at high pressure and high temperatures[J]. Soviet Physics Doklady,1965,9:1091-1098.
[3] LIU F S, YANG M X, LI Q W, et al. Shear viscosity of aluminum under shock compression[J]. Chin Phys Lett,2005,22(3):747-749.
[4] LI Y L, LIU F S, MA X J, et al. A flyer-impact technique for measuring viscosity of metal under shock compression[J]. Rev Sci Instrum,2009,80:013903.
[5] 马小娟,刘福生,李一磊,等. 冲击压缩下物质黏性系数与冲击波阵面扰动衰减特性研究[J] .物理学报,2010,59(7):359-362.
[6] VOCADLO L, DE WIJS G A, KRESSE G. First principles calculations on crystalline and liqiud iron at earth’s core conditions[J]. Faraday Discussions,1997,106:205-218.
[7] DESGRANGES C, DELHOMMELLE. Viscosity of liquid Iron under high pressure and high temperature:equilibrium and non equilibrium molecular dynamics simulation studies[J]. Phys Rev,2007,B76:172102.
[8] ZHANG Y, GUO G, NIE G. A molecular dynamics study of bulk and shear viscosity of liqiud Iron using embedded-atom potential[J]. Phys Chem Minerals,2000,27(3):164-169.
[9] 经福谦. 实验物态方程导引[M]. 2版. 北京:科学出版社,1999:82-85.
[10] STEINBERG D J, COCHRAN S G , GUINAN M W. A constitutive model for metals applicable at high-strain rate[J]. J Appl Phys,1980,51:1498-1501.
[11] MADER C H. Numerical Modeling of Explosives and Propellants[M]. Florida:CRC Press,1998:327-328.
[12] MA X J, LIU F S, JING F Q. Effects of viscosity on shock-induced damping of an initial sinusoidal disturbance[J]. Science China:Physics Mechanics and Astronomy,2010,53(5):802-806.
(编辑 余 毅)
Study on the Evolutionary Character of the Geometrical Disturbance on the Shock Front and the Strength of the Relevant Material
MA Haixia, MA Xiaojuan, KONG Gexing, LI Yong, HAO Binbin, LIU Fusheng
(KeyLaboratoryofAdvancedTechnologiesofMaterialsforMinistryofEducationofChina,SchoolofPhysicalScienceandTechnology,SouthwestJiaotongUniversity,Chengdu610031,Sichuan)
How to develop the non ideal spherical shock wave is one of the key problems. So the study of the relationship between the evolutionary character of the geometrical disturbance on the shock front and the dynamic properties of the relevant metal is an important subject in shock wave physics. In this paper, the two-dimensional finite difference method is used to simulate the flyer-impact disturbance experiment and the evolution of the disturbance on the shock front with the propagation distance in Aluminum is obtained. It is found that the yield strength is sensitive to the two characteristic points (the zero-amplitude point and the point with maximum amplitude of reverse-phase) on the disturbance amplitude damping curves, and the quantitative relation between them is listed. Therefore, this paper provides a theoretical basis for studying the strength effect of materials by the flyer-impact disturbance experiment, and opens a new way to study the strength properties of materials.
yield strength; disturbance on the shock wave; aluminum
2016-04-13
国家自然科学基金(2015G01154和11002120)和中央高校基本科研项目(SWJTU12CX085)
O521+21
A
1001-8395(2017)01-0090-04
10.3969/j.issn.1001-8395.2017.01.015
*通信作者简介:马小娟(1976—),女,副教授,主要从事高压物性以及物理力学的研究,E-mail:mxj_swjtu@126.com
