The Explicit Formula for the Smarandache Functionand Solutions of Related Equations
2017-05-15LIAOQunyingLUOWenli
LIAO Qunying, LUO Wenli
(Institute of Mathematics and Software Science, Sichuan Normal University, Chengdu 610066, Sichuan)
The Explicit Formula for the Smarandache Functionand Solutions of Related Equations
LIAO Qunying, LUO Wenli
(InstituteofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)
Letφ(n) andS(n) be the Euler function and Smarandache function for a positive integern, respectively. By using elementary methods and techniques, the explicit formula forS(pα) is obtained, wherepis a prime andαis a positive integer. As a corollary, some properties for positive integer solutions of the equationsφ(n)=S(nk) orσ(2αq)/S(2αq) are given, whereqis an odd prime andσ(n) is the sum of different positive factors forn.
Smarandache function; Euler function; Gauss function; perfect number
1 Introduction and Main Results
In 1918, Kempner[1]studied the formula of the value min{m:m∈N,n|m!}forafixedpositiveintegern.In1993,Smarandacheraisedsomeinterestingnumbertheoryproblems,andputforwordthedefinitionoftheSmarandachefunctionS(n)=min{m:m∈N,n|m!} for a positive integern. From the definition,S(1)=1,S(2)=2,S(3)=3, and so on. So far, there are some good related results[1-9]. For example, in [2], the distribution ofS(n) was discussed, and the asymptotic formula ofS(n) was given as follows
whereP(n) is the maximum prime factor ofn, andζ(s) is the Riemann-zeta function. In [3], Farris studied the bound ofS(n) and got the following upper and lower bounds

On the other hand, a lot of number theory equations related toS(n) have been studied in recent years. Especially, for a given positive integerk, many properties for positive integer solutions of the equationφ(n)=S(nk) were studied, whereφis the Euler function. Easy to see that this is equivalent to solve the equation
(*)
wherepis a prime, gcd(p,m)=1 andS(pαk)≥S(mk).

Theorem1.1Letpbeaprimeandαbeapositiveinteger.
1)Foranypositiveintegerrandα=pr,wehave
2)Foranypositiveintegerr, t∈[1,r]andα=pr-t,wehave
3)Foranypositiveintegerr, t∈[r+1,pr-pr-1]andα=pr-t.
(I)If
with
then we have
(1)
(II) If
witht∈[1,kn] and
then
(2)
Corollary 1.2 Letαbe a positive integer. If
then we haveS(2α)=α+n.
Fork=2,3,4, the solutions of the equation (*) have been discussed in [7]. In the present paper, we complement their results and obtain some necessary conditions for solutions of the equation (*).
Theorem 1.3 1) For any positive integerk, there are no any primepand positive integermcoprime withp, such thatφ(pm)=S(pk) andS(pk)≥S(mk).
2) For any positive integerk, if there are some primepand positive integermcoprime withp, such thatφ(p2m)=S(p2k) andS(p2k)≥S(mk). Thenp=2k+1 or 2≤p≤k. Furthermore,
(I) if 2k+1=p, then

(II) otherwise, i.e., 2≤p≤k, thenk≥3 and
3) For any positive integerk, if there are some primepand positive integermcoprime withp, such thatφ(pαm)=S(pαk) andS(pαk)≥S(mk). Thenαk+1>pα-3(p2-1) and 1≤φ(m)≤q, where
4) For any positive integerk, there exist some primepand positive integermcoprime withp, such thatφ(p3m)=S(p3k) andS(p3k)≥S(mk), namely,m=1,2.

2)Letpbeanoddprime, α≥1andn=2αp.




3)If2r-1isaprimeandn=22r-1(2r-1),then
Remark For convenience, throughout the paper we denote [·] to be the Gauss function.
2 The Proofs for Our Main Results
Before proving our main results, the following Lemmas are necessary.

2) For any primepand positive integerkwithk≤p, we have
Lemma 2.2 For any positive integerαand primep, we haveS(pα)≤(α-kα)p, wherekα(p+1)≤α<(kα+1)(p+1).
Proof For 0<α Now forα=m≥p+1, ifS(pm)=(m-km)pwith then Thus forα=m+1, we know that Hence we have two cases as following. (I) If thenkm+1=km. By the definition ofS(n), we haveS(pm+1)≤S(pm)+p, and so therefore in this case Lemma 2.2 is true. (II) Otherwise, we havem+1=(km+1)(p+1), and thenkm+1=km+1 andm-km=(km+1)p, where Note that therefore This means that Lemma 2.2 is true. By the definition ofS(n), we immediately have the following. Lemma 2.3 Letpbe a prime andmbe a positive integer. Then The Proof for Theorem 1.1 1) Sincepis a prime, and so Thus, by the definition ofS(n), we haveS(ppr)=pr+1-pr+p, and then (1) of Theorem 1.1 is proved. 2) Since andpr‖(pr+1-pr), and so for any positive integerrandα=pr-twitht∈[1,r], we haveS(pα)=pr+1-pr, thus (2) of Theorem 1.1 is true. 3) Forα=pr-twithr+1 (3) In fact, form=1, i.e.,α=pr-r-1, we have And then by the definition ofS(n), we can obtain which means that (3) is true form=1. Now suppose that (3) is true for anym=k(≥1), i.e., Then form=k+1, by Lemma 2.3, we have (A) or (B) For the case (A), by Lemma 2.3, we have and then which means that (3) is true. whichmeansthattheidentity(3)issatisfied. Fromtheabove,theidentity(3)istrue. Nowweprove(3)ofTheorem1.1. 1)Supposethatforanypositiveintegerk1andm=pk1such thatα=pr-r-pk1. Fromr+m∈[r+1,pr-pr-1], we haver+pk1∈[r+1,pr-pr-1], thus by the identity (3) and (1) of Theorem 1.1, we can obtain 2) Suppose that for any positive integerk1,s∈[1,k1] andm=pk1-s, such thatα=pr-r-(pk1-s). Fromr+m∈[r+1,pr-pr-1], i.e.,r+pk1-s∈[r+1,pr-pr-1], (3) and (2) of Theorem 1.1, we have 3) Suppose that there is some positive integerk1ande∈[k1+1,pk1-pk1-1], such thatm=pk1-e, namely,α=pr-r-(pk1-e). Fromr+m∈[r+1,pr-pr-1] we haver+pk1-e∈[r+1,pr-pr-1]. Now set then Similar to the previous discussions, we have the following three cases. 1′) If there is some positive integerk2such thatm1=pk2, i.e., and Thus by (3) and (1) of Theorem 1.1, we have which satisfies (1) of Theorem 1.1. 2′) Suppose that there is some positive integerk2andt1∈[1,k2], such thatm1=pk2-t1, i.e., and so Thus by (3) and (2) of Theorem 1.1, we have which satisfies (2) of Theorem 1.1. 3′) Suppose that there is some positive integerk2andt1∈[k2+1,pk2-pk2-1], such thatm1=pk2-t1, i.e., Now set then and so Similar to the previous discussions, we know thatα∈[pr-1,pr] is a positive integer. Thus, one can repeat the above discussions 1)-3). From the above discussions, Theorem 1.1 is proved. The Proof for Corollary 1.2 For any positive integerski(1≤i≤n) with 1≤k1 (**) Note that for anykm(1≤m≤n-1), we have Thus from (**) we can get Hence Thus Corollary 1.2 is proved. The Proof for Theorem 1.3 1) If there are some primepand positive integermcoprime withp, such thatS(pk)=φ(pm) andS(pk)≥S(mk). Then forp=2, we have Byφ(2m)≡ 0(mod 2) we havem≥3. While byS(2k)≥S(mk), we havem=1, this is a contradiction. And sop≥3, thus from the definition ofS(n) and the assumption thatpis coprime withm, we have 2) Suppose that there exist some positive integerα, primepand positive integermcoprime withp, such thatφ(p2m)=S(p2k) andS(p2k)≥S(mk). (I) For the case 2k≤p, by (2) of Lemma 2.1, we have i.e., 2k=(p-1)φ(m). Note thatpis a prime, ifp=2, then by 2k≤p=2 we havek=1, and soφ(m)=2, thusm=3,4,6. Hence from gcd(p,m)=1 andp=2, we can getm=3. In this case, which means that (p,m)=(2,3) is a solution. Now forp≥3, by 2k≤pwe have and soφ(m)=1, i.e.,m=1 or 2 andp=2k+1, hence (II) For the case 2k>p, suppose thatt1andt2are both nonnegative integers such that (4) and Then byS(p2k)=φ(p2m) and Lemma 2.2, we have (5) and Now from (5), we know that which means that (6) Note that 2k>p, i.e., 2kp>p2, thus we have three cases as following. 1) For the case which means that and sop2-1|p+2, i.e.,p+2≥p2-1. While 2) For the case i.e., 3) Therefore we must have (p2-1)φ(m)-(p+1)>p2, namely, By (6), we have i.e., (7) thus 2p2-(2k+1)p-3≤0, and so (8) Note thatpis a prime, and so 2p-(2k+1)≤1. If 2p-(2k+1)=1, then by (8), we know that (p,k)=(2,1),(3,2). From (p,k)=(2,1), we have 2k=p=2, this is a contradiction to 2k>p. Sok=2,p=3 or 2p<2k+1. Byk=2,p=3 and (7), we haveφ(m)=2, and thenm=3,4,6. Note that gcd(p,m)=1 and then forp=3, we havem=4, thus namely, (9) Note that whichisacontradiction.Hencek≥3,thusweprove(2)ofTheorem1.3. 3)Forα≥3.Ifαk≤p,thenby(2)ofLemma2.1,wehave thus henceαk=p=2,whichisacontradictiontotheassumptionα≥3.Andsoαk>p.Nowsupposethatt1andt2arebothnonnegativeintegerssuchthat (10) and (11) namely, thus and so i.e., (12) Note that for any positive integerm, we haveφ(m)≥1, therefore we must haveαk+1≥pα-3(p2-1). If i.e.,φ(m)=1. In this case, forα=3 we have 3k+1=p2-1, i.e.,p2=3k+2, which is impossible. Soα>3, and then We can conclude that (13) Otherwise, fromα-3≥pα-4(p-1)-1, we have (14) It is easy to see that forα≥4 there is no any primep>5 satisfying (14). Hencep=2 or 3. Byp=3 and (14) we haveα≥2(3α-4+1). While 2(3α-4+1)>αforα≥5. Therefore from (14) we haveα=4, and then 4k+1=3α-1-3α-3=24, which is a contradiction. Thus we must havep=2. Now fromp=2 and (14), we haveα>2α-4+2, and soα=4,5,6. Thus byαk+1=pα-1-pα-3andα=4, we haveαk+1=4k+1=23-2=6, which is a contradiction. Forα=5, we have 5k+1=12, which is also a contradiction. Forα=6,6k+1=24, it is also a contradiction. Hence (14) is not true, and soα-3 Now byφ(m)=1, gcd(p,m)=1 andφ(pαm)=S(pαk), we have this meanspα-3+p=pα-2. Note thatpis a prime, thus we havep=2 andα=4. And so 4k+1=23-2=6, which is a contradiction. From the above we must haveαk+1>pα-3(p2-1)≥p+1. Without loss of the generality, set Now by (12), we have (15) and so 1≤φ(m)≤q. Thus we prove (3) of Theorem 1.3. Thusweprove(4)ofTheorem1.3. FromtheaboveTheorem1.3isproved. we have i.e., (16) Thus from we have (17) wecanobtain1≤m≤d. ThusweproveTheorem1.4. TheProofforCorollary1.5 1)Ifp=2r+1isaprimeandα=2r,n=22r(2r+1).Then Ontheotherhand,bythedefinitionofσ(n)and(1)ofTheorem1.1,wealsohave 2)Sincen=2p-1(2p-1)isaperfectnumber,soσ(n)=2p(2p-1).Thusfrom(1)ofLemma2.1and2p-1isaprimenumber,wehave Notethat andso Bythesimilarway,wecanprovepart(3). ThusweproveCorollary1.5. Inthissection,someexamplesforbothTheorem1.1andCorollary1.2aregiven. Example3.1Letp=3,α=35=243,thenby(1)ofTheorem1.1wehave Ontheotherhand,from 163+54+18+6+2+0=243, and the definition ofS(n), we also haveS(3243)=489. Example 3.2 Letp=3,α=36-4=725. Namely, be takingr=6,t=4 in (2) of Theorem 1.1, we know that On the other hand, from 486+162+54+18+6+2+0=728, 485+161+53+17+5+1+0=722, and the definition ofS(n), we also haveS(3725)=1 458. Example 3.3 Letp=3,α=5 017, i.e., thus from (2) of Theorem 1.1, we have 4×2 187+16×81=10 044. On the other hand, from 3 348+1 116+372+124+ 41+13+4+1=5 019, and 3 347+1 115+371+123+ 41+13+4+1=5 015, we also haveS(35 017)=10 044. [1] KEMPNER A J. Miscellanea[J]. American Mathematical Monthly,1918,25(5):201-210. [2] XU Z F. The value distribution of Smarandache function[J]. Acta Mathematica Sinica,2006,49(5):1009-1012. [3] FARRIS M, MITSHELL P. Bounding the Smarandache function[J]. Smarandache Notions J,2002,13:37-42. [4] SMARANDACHE F. Only Problems, Not Solution[M]. Chicago:Xiquan Publishing House,1993. [5] GORSKI D. The pseudo-Smarandache function[J]. Smarandache Notions J,2002,13(1/2/3):140-149. [6] LE M H. A lower bound forS(2p-1(2p-1))[J]. Smarandache Notions J,2001,12(1):217-218. [7] LIU Y M. On the solutions of an equation invloving the Smarandache function[J]. Scientia Magna,2006,2(1):76-79. [8] 温田丁. Smarandache函数的一个下界估计[J]. 纯粹数学与应用数学,2010,26(3):413-416. [9] YI Y. An equation in volving the Euler function and Smarandache function[J]. Scientia Magna,2005,1(2):172-175. Smarandache函数的准确计算公式以及相关数论方程的求解 廖群英, 罗文力 (四川师范大学 数学与软件科学学院, 四川 成都 610066) Smarandache函数; 欧拉函数; 高斯函数; 完全数 O A 1001-8395(2017)01-0001-10 2016-01-03 国家自然科学基金(11401408)和四川省科技厅研究项目(2016JY0134) 廖群英(1974—),女,教授,主要从事编码和密码学理论的研究,E-mail:qunyingliao@sicnu.edu.cn Foundation Items: This work is supported by National Natural Science Foundation of China (No.11401408) and Project of Science and Technology 10.3969/j.issn.1001-8395.2017.01.001 (编辑 周 俊) Received date:2016-01-03 Department of Sichuan Province (No.2016JY0134) 2010 MSC:12E20; 12E30; 11T99











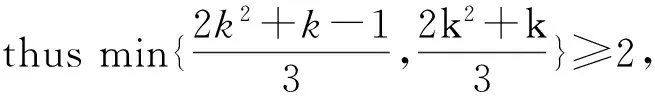



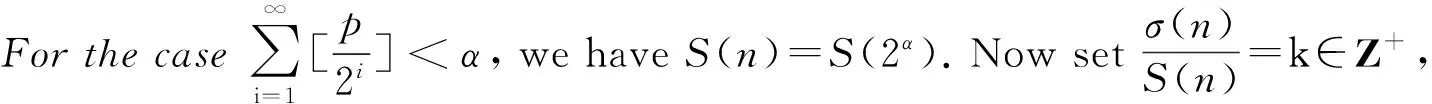





3 Some Examples
4 Conclusion


