一类带有指数反应项的非局部扩散方程的爆破分析

裴海杰, 杨 丽, 杜宛娟

(西华师范大学 数学与信息学院, 四川 南充 637009)

一类带有指数反应项的非局部扩散方程的爆破分析

裴海杰, 杨 丽, 杜宛娟*

(西华师范大学 数学与信息学院, 四川 南充 637009)

研究一类带有指数反应项的非局部扩散方程在Neumann边界条件下解的爆破性质.首先证明解的存在性、唯一性和比较原则,并在适当的条件下,证明解在有限时刻爆破.此外还得到解的爆破速率、爆破集以及对解的生命跨度的估计.

非局部扩散; 爆破; 有限时刻爆破; 爆破集; 爆破速率; 生命跨度

1 预备知识及主要结果

本文主要在Ω×(0,T)内研究如下非局部扩散问题的爆破性质

(1)

其中:奇数m>1,k>0均为参数;J:RN→R是一个非负有界的径向对称函数(J(z)=J(-z)),且满足

Ω为一个有界连通光滑区域;初值u0是非负非平凡的.

近年来,对非局部扩散的研究已经取得诸多成果,参看文献[1-5].方程

(2)

已被广泛应用于对非局部扩散过程的描述,例如人口动力学、化学反应、动力系统等.如果将u(x,t)视作种群在点x处t时刻的密度函数,J(x-y)为某种群从y地点迁移到x的概率分布函数,那么(J*u)(x,t)便是这个种群从其他地方迁到x处的速率[6].相应地

便可表示该种群从x地迁到其他地方的速率.如此考虑,在缺乏内源的条件下,将得到密度函数u满足非局部扩散方程(2)的结论.此外,由于种群在点x处t时刻的扩散不仅依赖于其密度u在(x,t)的值,并且通过卷积项J*u,扩散还与u在x邻近的值有关,因此方程(2)被称作非局部扩散方程.此外,方程(2)与经典热方程ut=△u具有许多相似性质.例如,它们的有界固定解为常数,均满足最大值原理,甚至在J是紧支的条件下,扰动的传播速度也是有限的.然而,在一般情况下是不满足正则性的影响.因此,对这类非局部扩散方程解的性质的研究就显得格外有意义.

文献[7]研究了如下的非局部扩散方程

(3)

其中,m>1,p>0,J:RN→R为一个有界非负函数,且满足

Ω⊂RN是一个有界光滑连通区域.在非负非平凡初值u0(x)的条件下,文献[7]得到了解的爆破速率及爆破集.

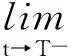
此外,在Ω区域内还有

定理 1.2 设u和v均是问题(1)的连续解,如果对任意x∈Ω有u0(x)≤v0(x),那么对一切(x,t)∈Ω×(0,∞),都有u(x,t)≤v(x,t)成立.

定理 1.6 (爆破集:一般情况)在一般区域Ω上考虑问题(1),其中k>1,奇数m>1.对于给定点x0∈Ω及ε>0,必存在初值u0(x)使得B(u)⊂Bε(x0)={x∈Ω:‖x-x0‖<ε}.

2 局部存在性、唯一性及比较原则

定义映射T:Xt0→Xt0为

那么,易得问题(1)的解恰好是以上映射在某个球域内(包含于Xt0)的不动点.

引理 2.1 上述定义的映射T映Xt0→Xt0.令u0和v0为非负函数,且u,v∈Xt0,那么存在正常数C使得

(4)

其中

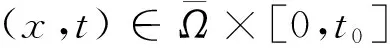
其中

于是Tu0(u)在t=0处连续.

因此,映射Tu0(u)在任意的t∈(0,t0]处连续.

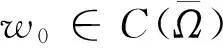
其中

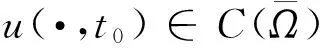
对变量x积分并使用Fubini定理有

注 2.1 函数u(x,t)是问题(1)的解当且仅当

注 2.2 问题(1)的解对初值的连续依赖性:如果u和v均是问题(1)的连续解,相应地,初值为u0与v0,那么存在常数C,使得对所有t0>0有

定理1.2的证明 假设u0(x)+δ0以及点x0∈Ω,使得u(x0,t0)=v(x0,t0),且对一切(x,t)∈Ω×[0,t0],有u(x,t)≤v(x,t).考察集合E={x∈Ω|u(x,t0)=v(x,t0)}.由x0∈E,所以E≠Ø.此外E为闭集.令x1∈E,则有

于是对任意y∈Br(x1),有u(y,t0)=v(y,t0),因此E是开集,所以E=Ω,矛盾.

对于连续的u(x,0)和v(x,0),考察递减的C1函数列un(x,0)和vn(x,0),在L1(Ω)意义下满足,当n→∞时有:

且un(x,0)≤vn(x,0).

令u(x,0)和v(x,0)分别为初值un(x,0)和vn(x,0)的解,则un(x,0)≤vn(x,0).让n→∞,结合注2.2和一致收敛定理,便得到定理1.2的结果.

3 爆破与爆破速率

定理1.3的证明 由于

对x在Ω上积分,使用Fubini定理和Jensen不等式得

注意到∫Ωu(x,t)dx不是全局的,u也不可能是全局的.对以上不等式积分便可得到对解的生命跨度估计

由(1)式知

(5)

对不等式(5)在区间(t,T)积分有

(6)

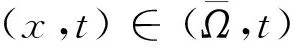
因为u(x,t)爆破,对某个ε>0和一个足够大的k,存在时刻t0使得对任意t∈(t0,T)有

同样在区间(t,T)上积分得

(7)

现让ε→0,结合(6)与(7)式可得

定理1.4证毕.

4 爆破集

下面给出问题(1)解的爆破集的一些结果.

假设u是问题(1)的解且在T处爆破.首先研究在对称区域上的情形,即定理1.5的证明.为简化工作,考察一维情况,即Ω=(-L,L),径向对称情形可相似处理.

首先证明一个引理：如果初始条件在原点处有唯一最大值,那么对每一个t∈(0,T),问题(1)的解在该点处有唯一最大值成立.

引理 4.1 对任意k,按照定理1.5的假设,则问题(1)的解是对称的,且满足ux<0,其中(x,t)∈(0,L]×(0,T).

证明 注意到u(-x,t)也是问题(1)的解,而对称性则可通过唯一性得到.

设w(x,t)=ux(x,t),那么w(x,t)满足方程

如果存在点(x0,t0)满足w(x0,t0)=0,由J′是奇函数以及u的对称性,易得一个矛盾.引理证毕.

定理1.5的证明 第一步,证明满足解的生命跨度估计条件的唯一爆破点为x=0.

给定x0>0,设ψ(t)=u(0,t)-u(x0,t)并应用均值定理,得到函数ψ(t)满足

其中

且ζ∈(0,x0).对该不等式积分可得

(8)

下面利用反证法构造一个矛盾,证明所需结论.

假设

由于

所以

因此存在ε>0,使得当ε→0+有

此外,如果u(0,t)有界,则有

(9)

结合(8)与(9)式可得

于是

矛盾,即证明了所需结论.

第二步,证明唯一可能的爆破点是原点.

考察函数

(10)

则Z(x,s)满足

由爆破速率可知

因此

(11)

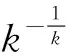
由比较原则知

(12)

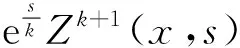
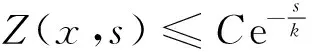
故u(x,t)≤C,即u(x,t)有界.定理1.5证毕.

(13)

考虑在x0的邻域内的u0,且越远离x0越小.设φ是一个非负光滑函数,且满足supp(φ)⊂Bε/2(x0)及φ(x)>0对所有x∈Bε/2(x0)成立.

现在令u0(x)=Nφ(x)+δ.选取足够大的N与足够小的δ使之满足(13)式.让N足够大,由定理1.3得

而且T可以任意的小.

再令φ(x,t)=eu(x,t),对爆破速率使用上界可得

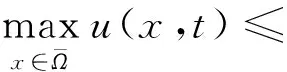
且

(14)

这样,φ(x,t)是下述方程的下解

(15)

(16)

只需证明在δ和T足够小时,(15)式的解w从t=0(或w(0)=eδ)到t=T均保持有界.为得到这个结论,采用文献[5]的方法.

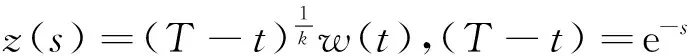
且

由于t=0,m是一个大于1的奇数,δ与T都足够小,得到

于是,对一切s>-lnT,z′(s)<0,且当s→∞,z(s)→-∞,定理得证.

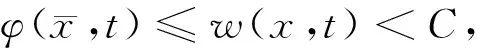
[1] BOGOYA M. Blowing up boundary conditions for a nonlocal nonlinear diffusion equation in several space dimensions[J]. Nonlinear Anal,2010,72(1):143-150.

[2] BOGOYA M. A nonlocal nonlinear diffusion equation in higher space dimensions[J]. J Math Anal Appl,2008,344(2):601-615.

[3] BOGOYA M, FERREIRA R, ROSSI J D. A nonlocal nonlinear diffusion equation with blowing up boundary conditions[J]. J Math Anal Appl,2008,337(2):1284-1294.

[4] IGNAT L I, PINASCO D, ROSSI J D, et al. Decay estimates for nonlinear nonlocal diffusion problems in the whole space[J]. J d’Analyse Mathé Matique,2014,122(1):375-401.

[5] PEREZ-LLANOS M, ROSSI J D. Blow-up for a nonlocal diffusion problem with Neumann boundary condition with reaction term[J]. Nonlinear Anal,2009,70(2):1629-1640.

[6] FIFE P. Trends in Nonlinear Analysis[M]. Berlin:Springer-Verlag,2003.

[7] 王玉兰,陈琼. 一类带有反应项的非局部扩散方程的爆破分析[J]. 四川大学学报(自然科学版),2012,49(2):299-303.

[8] LI Z P, MU C L. Global existence and blow-up analysis for a nonlinear diffusion equation with inner absorportion and boundary flux[J]. Dynamical Systems,2011,26(2):147-159.

[9] FRIEDMAN A, GIGA Y. A single point blow-up for solutions of semilinear parabolic systems[J]. J Fac Sci Univ Tokyo:Sect IA Math,1987,34(1):65-79.

[10] SAMARSKI A A, GALAKTIONOV V A, KURDYUMOV S P, et al. Blow-up in Quasilinear Parabolic Equations[M]. Berlin:Walter de Gruyter,1995.

[11] 杜清岭,周玉霞,黄臣程. 带有点源的非线性抛物方程解的淬灭[J]. 四川师范大学学报(自然科学版),2012,35(2):240-243.

[12] 王玉兰,夏安银,周斌. 一类具有势函数的多孔介质方程的爆破估计[J]. 四川师范大学学报(自然科学版),2013,36(4):549-553.

[13] 陈波涛. 一类广义非线性Schrödinger方程的爆破性质[J]. 四川师范大学学报(自然科学版),2011,34(4):499-504.

[14] 蒋良军. 具非局部源反应扩散方程组解的同时爆破与不同时爆破[J]. 应用数学,2014,27(3):652-657.

[15] 徐继军,郭从洲. 一类带有Neumann边界条件的反应扩散方程组解的整体存在性和爆破性[J]. 湖南师范大学学报(自然科学版),2013,36(5):12-14.

2010 MSC：35B44; 35B51

(编辑 李德华)

Blow-up Analysis for a Nonlocal Diffusion Equation with an Exponential Reaction Term

PEI Haijie, YANG Li, DU Wanjuan

(CollegeofMathematicsandInformation,ChinaWestNormalUniversity,Nanchong637009,Sichuan)

In this paper, we will mainly investigate the blow-up properties of a nonlocal diffusion equation with an exponential reaction term under Neumann boundary conditions. First, we prove the existence, uniqueness and the validity of a comparison principle of solutions. Then we show that solution blows up in a finite time within some proper conditions. Moreover, we will also study the blow-up rate, blow-up set and obtain the estimate for the life span of solutions.

nonlocal diffusion; blow-up; blow-up in finite time; blow-up rate; blow-up set; life span

2015-05-29

国家自然科学基金(11301419)和四川省教育厅自然科学重点项目(13ZA0010和14ZB0143)

O175.2

A

1001-8395(2017)01-0078-06

10.3969/j.issn.1001-8395.2017.01.013

*通信作者简介：杜宛娟(1981—),女,副教授,主要从事偏微方程的研究,E-mail:duwanjuan28@163.com