基于混沌PWM的SRM谐波频谱展开研究

孙嘉豪,王家军,郑致远

(杭州电子科技大学,杭州310018)

0 引 言

开关磁阻电动机(以下简称SRM)作为新发展起来的无级调速电动机,它的结构简单,成本低廉,能适应各种潮湿、高温甚至强振动的恶劣环境,并且可以保持高速运转,因此SRM是一种极具应用潜力的电动机。虽然SRM具有很多的优点,但是SRM本身也具有一些缺点,其中SRM的双凸极结构和固有的开关特性会使得SRM在运行过程中产生很大的噪声和机械振动,并限制了SRM在电机控制领域中的一些应用[1]。为了减缓SRM运行过程的噪声和机械振动问题,可以从两方面出发:一方面可以在电机设计阶段,优化SRM的电机结构参数;另一方面可以改变SRM调速系统的控制策略。对已经设计好的SRM进行控制,可以把相电流、开通角和关断角作为控制参数。本文主要运用混沌PWM技术对SRM的电压频谱展开,使电压谐波可以在较宽的频率范围内分布,在人听觉频率范围内的谐波幅值下降,从而降低SRM的脉动和噪声。

通常SRM的速度控制系统是双闭环,内环为电流环,外环为速度环。目前针对电流环的控制主要有3种不同的控制方法,它们分别是滞环控制、PWM控制和电流增量调制[2]。滞环控制具有动态性能好和实现比较简单的特点,缺点是开关的频率不确定,这将会引起很大的开关损耗和噪声问题。PWM控制是开关管的开关频率固定,但是在响应速度方面比滞环控制略差。在开关频率及其整数倍频率附近会导致电机产生机械振动和噪声。电流增量调制与滞环控制相似,其实现的电路是数字电路,此外其最大的开关频率受采样频率的限制。通过以上的分析可以看出这3种控制方法在抑制SRM噪声和脉动问题上仍然有很大的不足。

随着人们对电机噪声的关注,在1993～1994年间A.M.Trzynadlowsky和V.G.Agelidis等人提出了RPWM的方法[3]。这种方法通过改变噪声的频谱分布,使得功率变换器输出电压的谐波在总量不变的情况下,能够在比较宽的频率范围分布。因此,RPWM可以有效地降低电机的噪声和机械振动。根据实现的途径不同,RPWM可以分为3类,它们分别是随机开关频率PWM、随机脉冲位置PWM和随机开关PWM[4]。随机开关频率PWM是通过随机改变载波的频率或者三角波的斜率来产生PWM信号[5]。随机脉冲位置PWM是随机改变在开关周期内脉冲的位置来产生PWM信号,即改变周期内脉冲上升沿和下降沿的位置。随机开关PWM是用随机信号去代替三角波来产生开关控制的PWM信号。

RPWM的特点在于它的不确定性,这种不确定性可以通过随机数来实现。然而真正的随机数是很难产生的,因此实际中我们一般通过伪随机数发生器或者是混沌电路产生的伪随机数来代替随机数。伪随机数是由算法产生的,所以也是有规律的,只是变化的周期很长。人们发现混沌系统内在的随机性使得只需简单的迭代公式就能产生很复杂的运动。由混沌数作为伪随机数构造的RPWM称为混沌PWM(以下简称CPWM)。混沌数的产生一般是通过混沌电路来实现的。

本文基于RPWM进行谐波频谱展开可以将电压谐波分布在较宽频率范围的方法,通过混沌系统产生混沌序列来获得CPWM,并以四相8/6极SRM为对象,作谐波频谱展开研究。同时还将CPWM与电流滞环控制和传统PWM控制进行了比较,验证了其在降低SRM噪声和脉动的优越性。

1 混沌序列的产生方法

混沌序列的产生在上文已经提到,常见的混沌序列有逻辑映射混沌序列[6]、伯努利位移映射序列和帐篷映射序列。本文选择以逻辑映射混沌序列方法来产生混沌数。

逻辑映射属于二阶多项式映射,原本它是研究昆虫繁衍生息的数学模型,因其模型表达式比较简单,而且实现方式也比较容易,因此它目前被广泛应用于各种领域,尤其是在伪随机数的产生上应用最多。逻辑映射序列是离散的序列,它的数学表达式如下:

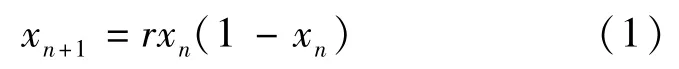
式中:xn代表了离散的混沌序列x的第n个数,它的取值范围是0～1;r是混沌序列的控制参数。混沌逻辑映射的初始条件x0取值范围是(0,1)。

经研究发现,根据控制参数r的取值不同,逻辑映射序列可以划分为以下3个区间:

(1)当r∈(0,3.57)时,离散序列表现为在(0,1)区间内周期变化或收敛的序列。

(2)当r∈(3.57,4]时,离散序列表现为在(0,1)区间内混沌变化的序列。

(3)当r∈(4,+∞)时,离散序列最终将会离开区间(0,1),并发散开。

逻辑映射的分叉图如图1所示,由逻辑映射产生的随机数如图2所示。

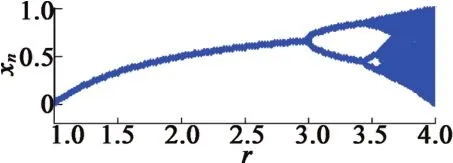
图1 逻辑映射产生的分叉图

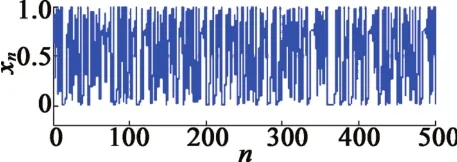
图2 逻辑映射产生的随机数

2 CPWM的设计

CPWM的结构框图如图3所示,主要由逻辑映射序列发生器、三角波周期计算、三角波发生器和比较器这4个部分组成。各部分主要功能如下所述。

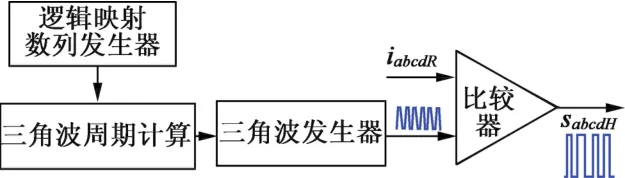
图3 CPWM的结构框图

(1)逻辑映射发生器主要是用来产生随机序列,xn的取值范围为(0,1)。xn决定了CPWM周期的不确定性。

(2)三角波周期值的大小可以由下面的公式计算得到:

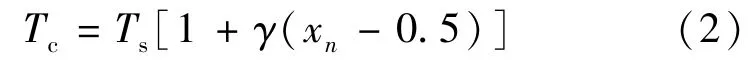
式中:Tc是随机载波周期;Ts是固定载波周期;γ是载波周期的调节增益。随着γ的增加,一方面谐波的峰值将会减小,另一方面随机载波周期也会发生变化。

(3)三角波发生器根据上面计算得到的随机载波周期Tc,就可以产生对应周期的三角波,并将得到的随机三角波送入到比较器。

(4)比较器的作用是输出CPWM。它有两个输入,一个是iabcdR(总参考电流分配到各相的电流),另一个输入是由三角波发生器输出的不同频率的三角载波。通过比较器后就可以输出各相所需的开关信号SabcdH。

3 系统仿真及结果

本部分将介绍SRM的控制系统结构,同时给出在滞环控制、传统PWM控制和CPWM控制下的仿真结果,并对结果进行了比较和系统分析。

3.1 SRM的控制系统

本文采用 MATLAB/Simulink进行建模仿真。仿真的SRM速度控制系统结构如图4所示。SRM的速度控制系统主要由速度控制器、电流分配单元、电流控制单元、功率变换单元和SRM电机本体5部分组成。各部分的详细说明如下:

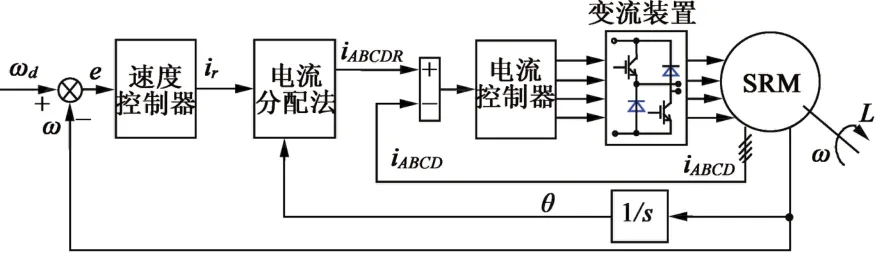
图4 SRM的速度控制系统

(1)SRM速度控制器是由比例微分控制器(以下简称PD)和具有滑模学习算法的自适应线性神经单元(Adaline)组成,它的作用是根据转速与给定值的差值,调节电流参考值的大小,使得转速能够很快地跟上给定的转速。

(2)电流分配法单元的主要功能是将电流参考值进行坐标变换,并进行正向化处理从而得到四相的参考电流。通过这种电流分配方法[7]可以极大地简化SRM的控制难度,使得控制只需要电机的相数,而不需要知道SRM的数学模型就可以保证SRM的速度控制。

(3)电流控制单元是由比例积分控制器(PI)和PWM单元组成。

(4)功率变换单元采用典型的不对称半桥回路。这种结构使得各相之间可以进行独立控制而互不影响,加之结构简单,因此可靠性较高。

(5)电机本体是四相8/6极的SRM,具体的电机参数如表1所示。

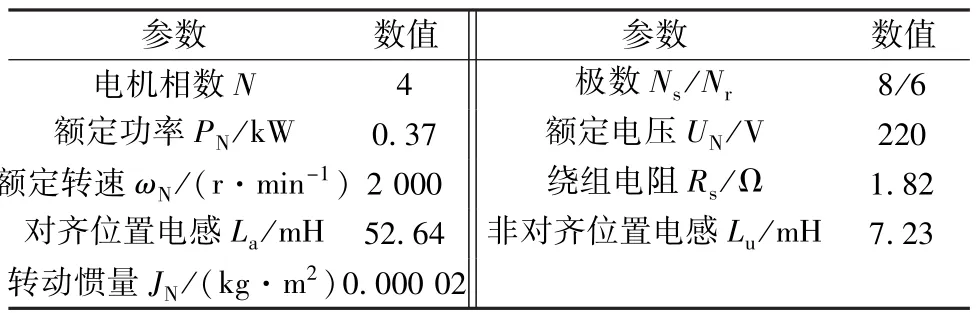
表1 8/6极SRM的参数

3.2 不同控制策略下的仿真结果

为了验证CPWM具有提高SRM谐波频谱展开的能力,下面将与滞环控制和传统PWM控制下的仿真作对比。3个仿真除了电流环采用不同的控制器,其它都保持一致。3个仿真的电流控制器分别采用了滞环控制、传统PWM控制和CPWM控制。3个仿真的给定速度为2 000 r/min,负载转矩为1.77 N·m。具体仿真结果如图5～图7所示。

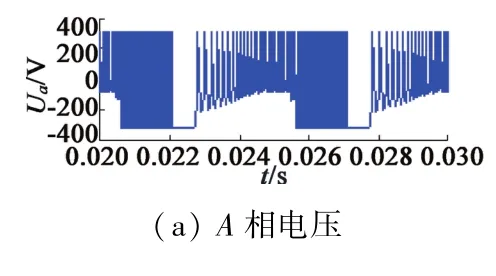
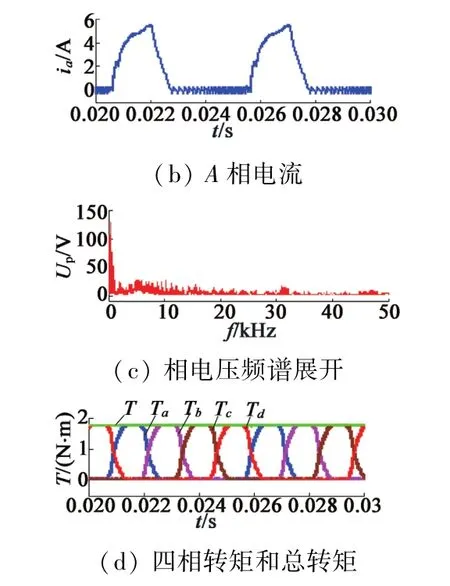
图5 SRM滞环控制下仿真结果

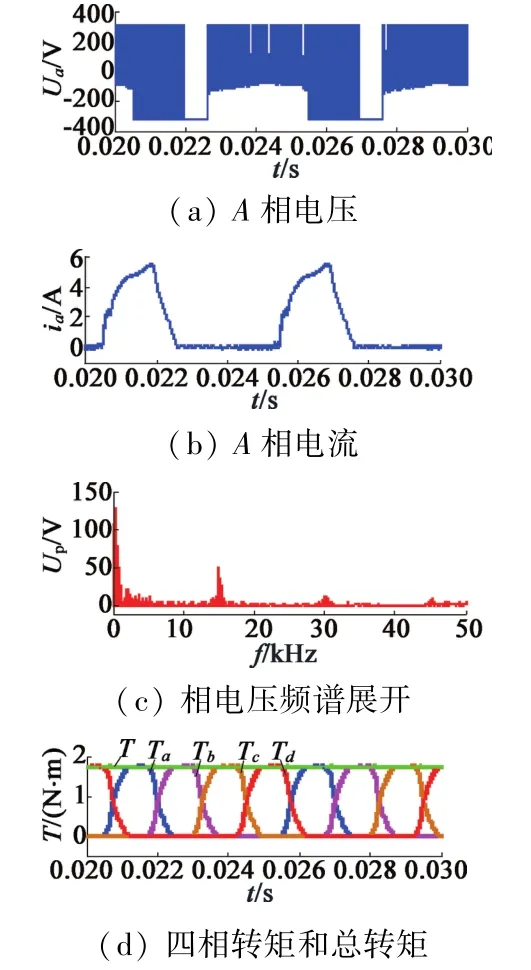
图6 SRM传统PWM控制下仿真结果

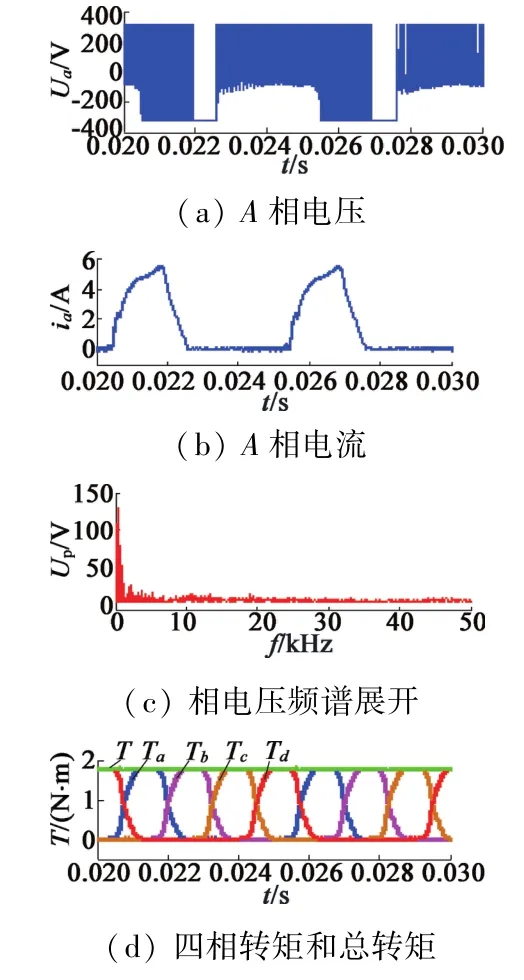
图7 SRM的CPWM控制下仿真结果

对于SRM的滞环控制,仿真设置的电流滞环宽度为0.2 A。从仿真结果图5(c)上不难发现,在频带0～35 kHz范围内电压谐波分量比较大。

对于传统的PWM控制,这里是基于电流分配方法的PWM控制。仿真把开关管的开关频率设置为15 kHz。从仿真结果图6(c)可以发现,在其开关频率附近以及整数倍频率附近电压谐波的幅值较大。

对于CPWM控制,仿真设置的载波周期调节增益γ为0.5,固定载波周期Ts为6.67×10-5s。从图7(c)可知,电压谐波分量在频带范围内较小,尤其是在人耳能够听得到的频带20 Hz～20 kHz范围内的谐波分量都比较小。

这里只给出电压谐波的频谱展开,这是因为电流谐波与之是相关联的,它们之间相差个阻抗。从图中我们可以看到在某一相转矩为零的情况下,电压不为零,这是由于采用电流分配方法考虑了换相的过渡,即存在两相导通的情况,这也就解释了此时相电流也不完全为零,而是在一个很小幅度变化。

4 仿真计算和分析

4.1 性能指标HSF和THD的计算

为了对SRM谐波频谱展开性能进行评估,把HSF和THD作为评估指标。定义和表达式如下:

HSF表达式如下[8]:

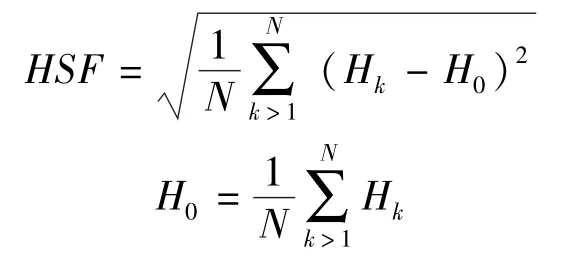
式中:HSF是谐波展开因子;Hk是k次谐波的振幅大小;H0是除基波以外的所有N次谐波的平均值。HSF描述了随机载波频率PWM谐波频谱展开的影响。这个数值越小,表示谐波抑制效果越好。

THD表达式如下:

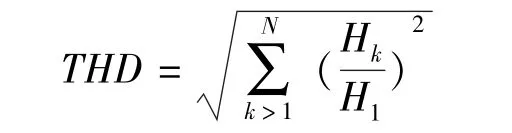
式中:THD是总谐波失真,H1是基波分量。THD的数值越小,意味着谐波的峰值越小,同时电磁辐射和损失也越小。

在计算HSF和THD过程中,SRM基波频率的计算公式如下:

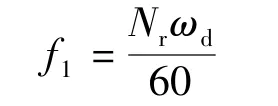
式中:f1是SRM的基频;Nr是转子表面凸出极的个数;ωd是电机的理想转速。

4.2 仿真结果分析

HSF与THD在不同SRM控制方式下的计算值如表2所示。具体分析如下:

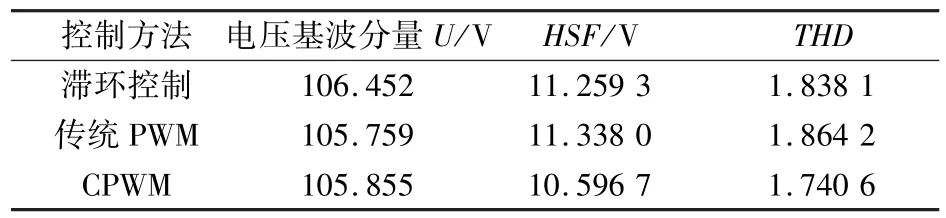
表2 不同控制策略下的谐波频谱展开性能计算

在CPWM控制下,SRM的电压基波分量相对滞环控制下略小,和PWM控制相比差不多,因此可以认为其对基波分量的影响忽略不计。

在相同的条件下,与滞环控制和传统PWM控制相比,CPWM控制下的HSF和THD的值更小。这表明在抑制谐波方面,CPWM具有优越性。

从上分析可以发现CPWM具有较好的谐波频谱展开性能,对降低SRM噪声和振动的研究具有重要的意义。

5 结 语

为了解决SRM噪声和振动的问题,本文基于RPWM具有较好的谐波频谱展开能力的思想,运用CPWM技术对SRM电压谐波进行频谱展开,使谐波在较宽的频率范围内分布,从而局部谐波幅值得到降低。最后通过仿真进行了验证。本文可以得到以下结论:

(1)逻辑映射混沌系统产生的伪随机数能够保证CPWM具有较好的随机性。

(2)CPWM能够对SRM的谐波进行频谱展开,同时能够降低SRM的噪声和振动。

(3)通过仿真结果的比较和相应评估指标的计算,可以看出与滞环控制和传统PWM控制相比,CPWM具有更好的谐波频谱展开能力。

参考文献

[1] WU C Y,POLLOCK C.Analysis and reduction of vibration and acoustic noise in the switched reluctance drive[J].IEEE Transactions on Industry Applications,1995,31(1):91-98.

[2] BLAABJERG F,KJAER P C,RASMUSSEN P O,et al.Improved digital current control methods in switched reluctance motor drives[J].IEEE Transactions on Power Electronics,1999,14(3):563-572.

[3] AGELIDIS V G,VINCENTI D.Optimum non-deterministic pulsewidth modulation for three-phase inverters[C]//Proceedings of International Conference on IEEE Industrial Electronics Control,and Instrumentation,1993:1234-1239.

[4] KIM K S,JUNG Y G,LIM Y C.A new hybrid random PWM scheme[J].IEEE Transactions on Power Electronics,2009,24(1):192-200.

[5] HABETLER T G,DIVAN D M.Acoustic noise reduction in sinusoidal PWM drives using a randomly modulated carrier[J].IEEE Transactions on Power Electronics,1991,6(3):356-363.

[6] MAYNARD S J.Mathematical ideas in biology[M].Sussex:The University Press,1968.

[7] WANG J J.A common sharing method for current and flux-linkage control of switched reluctance motor[J].Electric Power Systems Research,2016,13(1):19-30.

[8] LAI Y S,CHANG Y T,CHEN B Y.Novel random-switching PWM technique with constant sampling frequency and constant inductor average current for digitally controlled converter[J].IEEE Transactions on Industrial Electronics,2013,60(8):3126-313.