UR机器人的运动学和奇异性分析*

□郭小宝 □罗振军 □赵振

杭州娃哈哈集团机电研究院智能装备研究所杭州310020

UR机器人的运动学和奇异性分析*

□郭小宝 □罗振军 □赵振

杭州娃哈哈集团机电研究院智能装备研究所杭州310020

机器人的正向、逆向运动学是研究机器人运动姿态控制的理论工具，其封闭解问题目前还没有通用解法，比较常用的是代数方程组数值迭代算法，但难以保证实时性和精度要求。基于矩阵理论分析UR型机器人的机构特点，采用解析方法获得正向运动学和逆向运动学解法，进而获取机器人的奇异位置，最后通过MATLAB编程和SolidWorks三维实体模型运动仿真验证解法的正确性。

1 课题背景

丹麦创新工业机器人制造商Universal Robots公司的UR5及UR10型机器人凭借优异的灵活度、安全性和独特创新的人机协同功能，在近年来的各届工业展览会上受到越来越多的关注。2012年5月，UR5型机器人被国际机器人学联合会（IFR）及美国电气和电子工程师协会机器人与自动化学会（IEEE-RAS）评为全球最创新机器人。UR机器人颠覆了笨重且昂贵的传统工业机器人概念，它凭借创新的技术能够让操作者迅速掌握操控技巧，并投放至多个生产流程中[1-2]。

UR机器人是一种六关节机器人，目前国内对其机构运动学的研究较少。机器人的正向、逆向运动学是研究机器人运动姿态控制的理论工具，是指导机器人动作指令的核心部分，简单且能够快速执行的运动学算法是机器人实现高速、高精度运行的重要手段[3-4]。

机器人的正向运动学是在已知关节变量的情况下，求解末端执行器的空间位置和姿态；逆向运动学则是在已知末端执行器位置和姿态的情况下，求解关节变量。机器人运动学算法主要有解析法和数值法。解析法包括矢量代数法、几何法、矩阵法和四元数法等，优点是可以得到全部解，缺点在于难度较大，方法通用性不强。数值解法直接求解约束方程组，可以通过迭代运算求得任何机构的实数解，但通常不能得到全部解，一般而言，初值的选取及搜索算法对收敛性和精度影响较大[5-10]。

基于机器人通用的D-H（Denavit-Hartenberg）矩阵方法，根据机构的结构组成特征建立约束方程组，采用多种方法从约束方程组中消去中间参数，获得单参数多项式后再求解，并详细推导正向运动学和逆向运动学解法及机器人奇异位置，推导过程简单、直观。最后通过工程实例，采用MATLAB编程和SolidWorks三维实体模型运动仿真验证运动学解法的准确性。

2 UR机器人运动学模型

UR机器人三维模型如图1所示，这是一种六自由度机器人，包括底座、腰部、大臂、小臂、手腕头、手腕尾、末端法兰7个基本部件，相邻两个部件之间通过转动关节连接。

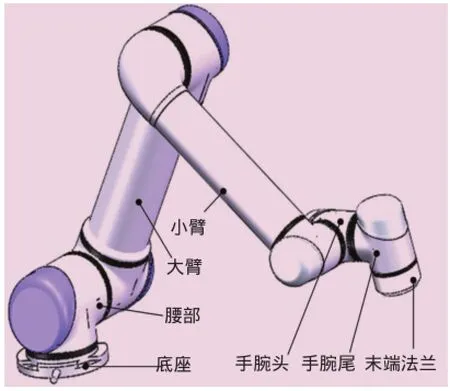
图1 UR机器人三维模型

相比传统的六自由度机器人，UR机器人具有各个关节都能整周回转的优点，且由于UR机器人机构特点满足机器人机构学的Pieper准则[11]，因此其运动学逆解具有封闭解的优势，使运动控制更为容易。

图2 UR机器人机构简图

UR机器人6个转动关节轴线Ai中，A1和A2相互垂直，A2、A3、A4相互平行，A4和A5相互垂直，A5和A6相互垂直。采用D-H矩阵分析法建立各个关节连杆坐标系，机器人杆长参数见表1。

表1 机器人杆长参数和关节变量

3 UR机器人运动学算法研究

机器人运动学主要解决机器人驱动关节变量与末端刚体位姿坐标（操作空间变量）之间的映射关系，可以为机器人的运动控制提供理论基础，是实现机器人闭环实时精确控制的重要一环。

3.1 正向运动学

为了简化三角函数符号，下文中用ci表示cosθi的值，用si表示sinθi的值，用c234表示的值，用s234表示sin（θ2+θ4+θ4）的值。

连杆之间变换矩阵可以表示为：

由此，可以求出连杆变换积：

从而正向运动学可以表示为：

3.2 逆向运动学

对比式（9）和式（10），矩阵的第2行第4列元素为常数，即可获得求解θ1的一元方程：

通过三角函数万能公式，可求出θ1：

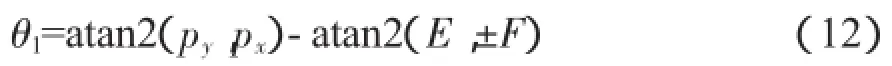
然后可求解θ5和θ6，对比式（9）和式（10），由矩阵的第2行前三列元素可以获得关于θ5和θ6的方程：

联立式（13）和式（14），消除变量，得：

联立式（15）和式（16），即可求出θ5：

观察式（13）和式（14），可得：当s5=0，即θ5=0或θ5=π时，机构发生奇异，无法求出θ6；当s5≠0，即θ5≠0且θ5≠π时，可以求出θ6：

对比式（9）和式（10），由矩阵第1行第3列和第3行第3列两列元素可以导出如下方程：

当s5=0，即θ5=0或θ5=π时，机构发生奇异，无法求出θ2+θ3+θ4；当s5≠0，即θ5≠0且θ5≠π时，此时可以求出θ2+θ3+θ4：

对比式（9）和式（10），由矩阵第1行第4列和第3行第4列两列元素可以导出如下方程：

2.4 血糖（Glu）和皮质醇（Cor） 两组病人组间比较，T3、T4时间点B组Glu和Cor均高于A组，且差异有统计学差异（P＜0.01）。A组Glu于T4时明显高于T1（P＜0.05）；A 组 Cor于 T3、T4时较 T1显著升高（P＜0.01）。 B 组 Glu 于 T2～T4时明显高于 T1（P＜0.01）；B组 Cor于 T3、T4时明显高于 T1(P＜0.01)。 见表 4。

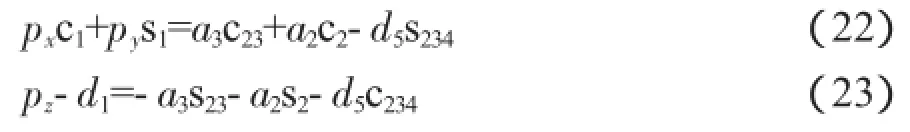
联立式（22）和式（23），消除变量θ2+θ3，可以获得求解θ2的一元方程：

从而可以求解出θ2：

在求解θ2后，再次联立式（22）和式（23），即可求出θ2+θ3：

从而可以求出θ3与θ4。

至此，逆向运动学的结果，即6个关节变量均已求出。

4 UR机器人奇异性分析

机器人在奇异点位置时，逆向运动学求解表达式无解，无法通过逆向运动学运算将末端笛卡尔坐标系转化为关节电机轴的角度，而且笛卡儿坐标系内一点微小的变化就会引起轴角度的剧烈变化，所以需要获得奇异点位置的直观表达，避免机器人失控。

（2）肘部奇异位置表达式。当A2+B2-C2=0时，无法求出θ2，导致机构失控，轴线z2、z3、z4共面。

（3）腕部奇异位置表达式。当s5=0，即θ5=0或θ5=π时，轴线z4和z6平行，无法求出θ6，导致机构失控。

5 工程实例验证

5.1 MATLAB验证

在MATLAB开发环境下，根据前述运动学算法编写如图3所示的正向、逆向运动学算法脚本，脚本代码不足30行，完全为顺序结构，没有任何数值迭代，具有较快的执行速度。

图3 运动学算法MATLAB脚本截图

运动学测试点如下。

通过MATLAB校验，运动学测试点满足正向运动学和逆向运动学算法，从而验证了解法的有效性和正确性。

5.2 运动仿真验证

为了反映运动学算法的真实性，在SolidWorks三维建模软件下设计UR机器人模型，定义配合和约束条件。

验证时，规划机器人工作空间末端法兰的运动轨迹，在y-z平面上的轨迹如图4所示。

图4 机器人末端控制点在y-z平面内轨迹

通过逆向运动学和轨迹规划，计算出各驱动轴的关节角位移，如图5所示。

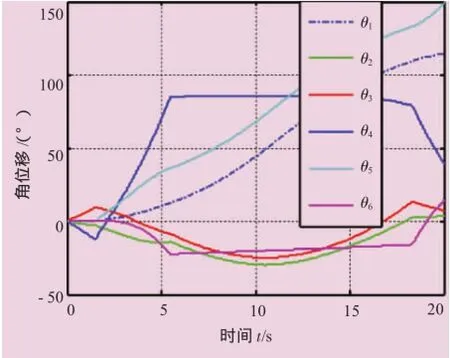
图5 各驱动轴关节角位移曲线

将各关节的角位移导入基于SolidWorks设计的UR机器人模型，作为各关节驱动伺服电机的输入量，经过实时运动仿真获得如图6所示的模拟轨迹，该模拟轨迹与预先规划的轨迹完全一致，从而验证了运动学解法的正确性。

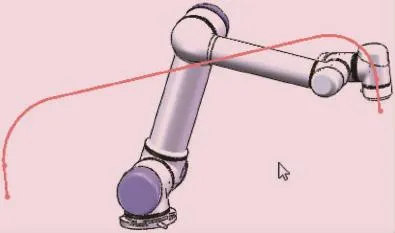
图6 UR机器人运动仿真末端模拟轨迹

6 结论

基于D-H矩阵法研究了UR机器人运动学的解析算法，得出了结论。

（1）分析了UR机器人的机构类型，得出了其具备运动学封闭解的条件。

（2）通过D-H矩阵法，根据UR机器人机构的结构组成特征建立约束方程组，获得了简单直观的运动学算法。

（3）通过分析得出了UR机器人三种类型奇异的数学表达式，为机器人机构奇异处理和运动控制提供了重要参考。

（4）以MATLAB和SolidWorks软件为工具，通过三维运动仿真验证了UR机器人运动学解法的正确性和有效性。

[1]博达.Universal Robots（优傲机器人）推出UR3新型机器人——全球最灵活轻便[J].机械制造，2015,53（4）：13.

[2]石强.UR:让“力控制”感知你[J].今日工程机械，2013（10）：68-69.

[3]钱晖.多传感器融合技术在智能机器人系统中的应用[J].上海电气技术，2010，3（2）：44-48.

[4]王昊杰,薛强.一种三坐标并联动力头——Sprint Z3的运动学逆解及尺度综合[J].机床与液压,2011,39（17）：53-56.

[5]郭小宝,赵振,陈落根.码垛机器人运动学几何解法的研究[J].装备机械,2015（4）：44-47.

[6]黄真，赵永生，赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.

[7]陆晶，高国琴，朱彩红，等.新型三平移并联机构的运动分析和工作空间分析[J].机械设计与制造，2007（11）：163-165.

[8]LI Y M，XU Q S.Kinematic Analysis of a 3-PRS Parallel Manipulator[J].Robotics and Computer-Integrated Manufacturing，2007,23（4）：395-408.

[9]刘辛军,汪劲松,李剑锋，等.一种新型空间3自由度并联机构的正反解及工作空间分析[J].机械工程学报,2001，37（10）：36-39.

[10]蔡自兴.机器人学[M].北京：清华大学出版社,2000.

[11]熊有伦.机器人技术基础[M].武汉：华中理工大学出版社，1996.

（编辑：启德）

The forward and reverse kinematics of robots are the theoretical tools for researching the control of robot motion attitude.There is no general solution for its closed solution.Numerical iterative algorithms with algebraic equations is used more commonly,but it is difficult to guarantee real-time and accuracy requirements. Based on matrix theory,analyzed the mechanical feature of UR robot and obtained the solution for forward kinematics and inverse kinematics by using analytic method,and thus the singular position of the robot could be obtained.Finally,the correctness of the solution was verified by motion simulation established by MATLAB programand 3D solid model in SolidWorks.

机器人；运动学；奇异性；矩阵

Robot；Kinematics；Singularity；Matrix

TH242.2

A

1672-0555（2017）01-001-05

*国家科技重大专项（编号：2011ZX04013-011）

2016年8月

郭小宝（1988—），男，硕士，助理工程师，主要从事机器人结构设计和运动控制研究工作