基于定子电压定向的自适应控制在电网故障下双馈异步发电机的优化运行策略*

陆 畅, 武振宇, 胡军台, 付 晓

(国网河南省电力公司 平顶山供电公司，河南 平顶山 467001)

基于定子电压定向的自适应控制在电网故障下双馈异步发电机的优化运行策略*

陆 畅, 武振宇, 胡军台, 付 晓

(国网河南省电力公司 平顶山供电公司，河南 平顶山 467001)

提出了一种基于定子电压定向(SVO)的定子磁链动态过程改进控制方案，引入积分环节到转子电流控制器，消除电压故障状态产生的静差，通过自适应调节补偿定子电阻，联合优化的最大功率跟踪器，增强风电机组供电质量，提高系统的稳定性和鲁棒性。基于PLECS算例分析验证，在出现电网电压瞬态跌落故障和电网谐波下，即使风机运行在次同步或超同步状况，提出的控制策略都可以实现谐波抑制，减小定、转子功率振荡、电磁转矩脉动、传动系统机械损耗，为进一步高渗透率风电场研究提供依据和参考。

定子电压定向；电能质量；最大功率跟踪；双馈异步发电机；瞬态跌落；谐波

0 引 言

随着化石能源的紧缺，传统发电带来的环境污染，以及气候治理等问题，发展可再生能源，特别是风电、太阳能已成为国内主要经济体能源转型的主要方向。但风电场接入地区网架比较薄弱,以及风电的间歇性、随机性、波动性和不可控性，大型集群风电接入必然会给电力系统注入更多的不确定性[1]。目前对风电并网控制的研究，大多建立在理想电网情况，因此，有必要对非理想电网电压，特别是电压瞬态跌落及电压谐波问题进行讨论。

风电场的大规模建设，给电网规划和运行都带来了挑战，加之我国的电网结构相对薄弱，使得风电并网研究及风电并网后的运行带来了巨大的挑战[2-3]。研究大规模风电并网引起的电力系统运行与稳定的问题，并提出相关的技术解决措施是风电发展的关键。文献[4]提出了基于滑模控制理论的一种降低风电机组载荷的多目标变桨距控制策略，但由于控制目标的增多导致桨距角调节更加频繁，且所设计方法复杂，难以实际投入运行。文献[5-7]在含风电场的电力系统经济调度模型中考虑价格、型号需求响应，以提高系统的风电消纳能力。文献[8]为缓解大规模风电并网给电力系统频率带来的不利影响， 设计了基于分段控制思想的双馈风电机组频率控制策略，但其控制所基于的风力发电经济函数与实际有差，其方法需进一步验证。文献[9]针对电网电压骤变、电压不平衡、谐波畸变等，将谐振控制器引入锁相环(Phase Locked Loop,PLL)中，增强了双馈异步发机(Doubly Fed Induction Generator,DFIG)适应电网的能量，但未分析如何控制风机运行在最大功率情况，故该控制策略还需进一步完善。上述研究主要从目前风电运行特性分析，通过加入额外的控制环增强系统的供电质量，但方法并未充分考虑电网特性给风电带来的扰动并同时保证最大功率实现。

本文从风力机的运行特性、发电机输出功率控制与风电机组最大风能追踪运行的实现分析，建立了PWM变流器数学模型。通过分析传统控制方法的不足，提出了基于定子电压定向(Stator Voltage Oriented，SVO)改进定子磁链动态矢量控制方案，实现在电网电压瞬态跌落故障时，大幅度减小电流电压畸变程度，减小定转子功率振荡和传动系统的机械损耗，以及电网带来的谐波影响等，并增强系统的可靠性与鲁棒性。最后，在PLECS搭建的仿真模型中，考虑不同电网电压故障程度及电网电压含大量谐波工况时，通过传统控制策略与提出的改进控制方法的对比分析，验证提出的改进优化控制方案的有效性。

1 双馈机组数学模型

DFIG能与电网柔性连接，实现有功和无功功率的控制，还可跟随风速变化捕获最大风能，其模型由风力机模型、桨距角控制模型及双馈机组动态模型等组成[10]。

1. 1 风力机模型

风力发电系统主要由风力机和发电机组成，风力机作为风力发电系统的首要环节，用于截获流动空气所携带的动能，并将其中一部分转换为机械能；因此。风力机决定了整个风力发电系统的输出功率。

根据空气空力学知识，风力机输入功率表示为

(1)

式中：ρ——空气密度；Sw——风力机叶片迎风扫掠面积；v——进入风力机扫掠面之前的空气流速(即未扰动风速)。

由于通过风力机叶片的风能并不能完全被风力机吸收，可定义风能利用系数Cp来表示风力机吸收风能的能力，且Cp=P0/Pv。其中P0为风力机输出功率，Pv为输入风轮面内功率。因此，风力机的输出功率可表示为

(2)

式中：Dw——风轮的直径。

风能利用系数与风速、叶片转速、风轮直径、桨距角均有关。为分析Cp的特性，将叶尖速比λ定义为叶片尖端的线速度与风速之比，即：

(3)

式中：Rw——风轮半径，Rw=0.5Dw；ωw——叶片旋转角速度；nw——叶片的转速。

采用变桨距的风力机特性曲线通常由一簇风能利用系数Cp的曲线来表示。风能利用系数Cp是叶尖速比λ、桨距角β的综合函数，即Cp(λ，β)，如图1所示。由图1可知，当桨距角增大时，Cp(λ)曲线将显著缩小；若保持β不变，Cp只与叶尖速比λ有关。

图1 变桨距风力机性能曲线

1. 2 双馈机组动态模型

1. 2. 1 电压方程

定子绕组和转子绕组电压方程分别为

(4)

式中：usd、usq,urd、urq——定、转子电压的d、q轴分量；

ψsd、ψsq,ψrd、ψrq——定、转子磁链的d、q轴分量；

isd、isq,ird、irq——定、转子电流的d、q轴分量；

Rs、Rr——定、转子绕组电阻；

ωr——转差电角速度。

1. 2. 2 磁链方程

与dq坐标系下电压方程的方法类似，可得磁链方程：

(5)

式中：Lm——dq坐标系中定、转子同轴等效绕组间的互感，Lm=1.5Lms；

Ls——dq坐标系中定子等效两相绕组自感，Ls=Lm+Lls；

Lr——dq坐标系中转子等效两相绕组自感，Lr=Lm+Llr。

采用两相绕组等效代替三相绕组，定、转子同轴等效绕组间的互感Lm是原三相绕组中任意两相间最大互感(轴线重合时)的3/2倍。从式(5)可以看出，由于互相垂直两轴之间没有耦合，互感磁链只在同轴绕组间存在。

1. 2. 3 转矩方程

根据机电能量转换原理，发电机电磁转矩为

(6)

式中：Te——发电机的电磁转距。

1. 2. 4 运动方程

(7)

式中：TL——风力机提供的驱动转矩；J——风电机组的转动惯量；D——与转速成正比的阻转矩阻尼因数；K——扭转弹性转矩因数。

若D=0，K=0，则有:

(8)

式(8)表示为一个非线性、时变、强耦合的多变量系统，必须通过坐标变换来实现解耦。可用任意旋转dq坐标系来简化坐标变换的运算。

2 基于SVO的改进定子磁链动态矢量控制方案

传统的DFIG控制模型中，采用定子磁链定向(Stator Flux Linkage Orientation，SFO)的同步旋转坐标系模型和SVO的同步旋转坐标系模型，从而形成基于SVO的矢量控制策略。但传统矢量控制策略都建立于电网电压恒定、忽略定子励磁电流动态过程的DFIG简化模型。在电网电压故障情况下，基于传统的矢量控制方案动态稳定性和鲁棒性较差，严重时还会发生输出功率大幅振荡的现象。

通过引入积分环节，消除电压故障状态产生的静差，以式(9)为设计依据。

(9)

进一步，可得到改进的DFIG转子侧变流器输出电压参考值为

(11)

其中：ωslip=ω1-ωr。

根据式(9)～式(11)可得定子励磁电流动态过程的SVO改进矢量控制框图，如图2所示。与传统SVO矢量控制相比，改进控制方案引入了定子励磁电流的微分项作为补偿项，在传统控制中，则被认为是零而忽略，即urd1=urq1=0。

与传统控制方案相比，改进的SVO定子磁链动态控制方案在原来控制器基础上加入了计及定子励磁电流变化的补偿量Lm/Ls(Us-RsIs-jω1Ψr)，以此对解耦电路作出修正。由于引入电流交叉耦合项、转子电压降及定子磁链前馈补偿等，从而实现了d、q轴电流的解耦控制，有效提高了系统的动态控制性能，提高了网侧变流器的抗负载扰动性能。此外，Lm/Ls=Lm/(Ls+Lσs)≈1，则补偿量中与模型参数有关的量仅为定子电阻Rs，通过自适应调节可测量Rs，可实现电网电压故障补偿，增强系统可靠性与鲁棒性。

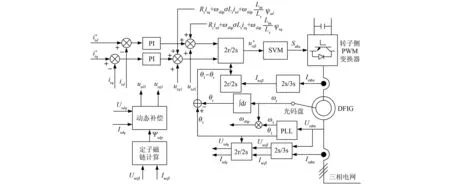
图2 改进SVO矢量控制框图

3 改进DFIG最大风能追踪的实现

根据最大风能追踪运行机理，有功功率参考值为DFIG风电机组实现最大风能追踪关键。不计机械损耗的条件下，DFIG输出总电磁功率参考值为

(12)

其中：

式中：ωm——发电机转子机械角速度；ωr——发电机转子电角速度；N——DFIG齿轮箱变比；p——DFIG极对数。

采用优化策略的电磁功率参考值为

(13)

4 仿真试验

为验证提出的改进SVO的定子磁链动态矢量与最大风能追踪实现策略的有效性，在PLECS平台上采用2 MW双馈异步风力发电系统进行仿真分析，并将电网电压故障分为瞬态跌落80%，以及稳态2%的不平衡度和电网电压谐波。详细的控制参数如表1所示，仿真通过次同步运行状态、超同步运行状态以及次同步到超同步的过渡过程三个方面来验证提出的DFIG控制策略的有效性。

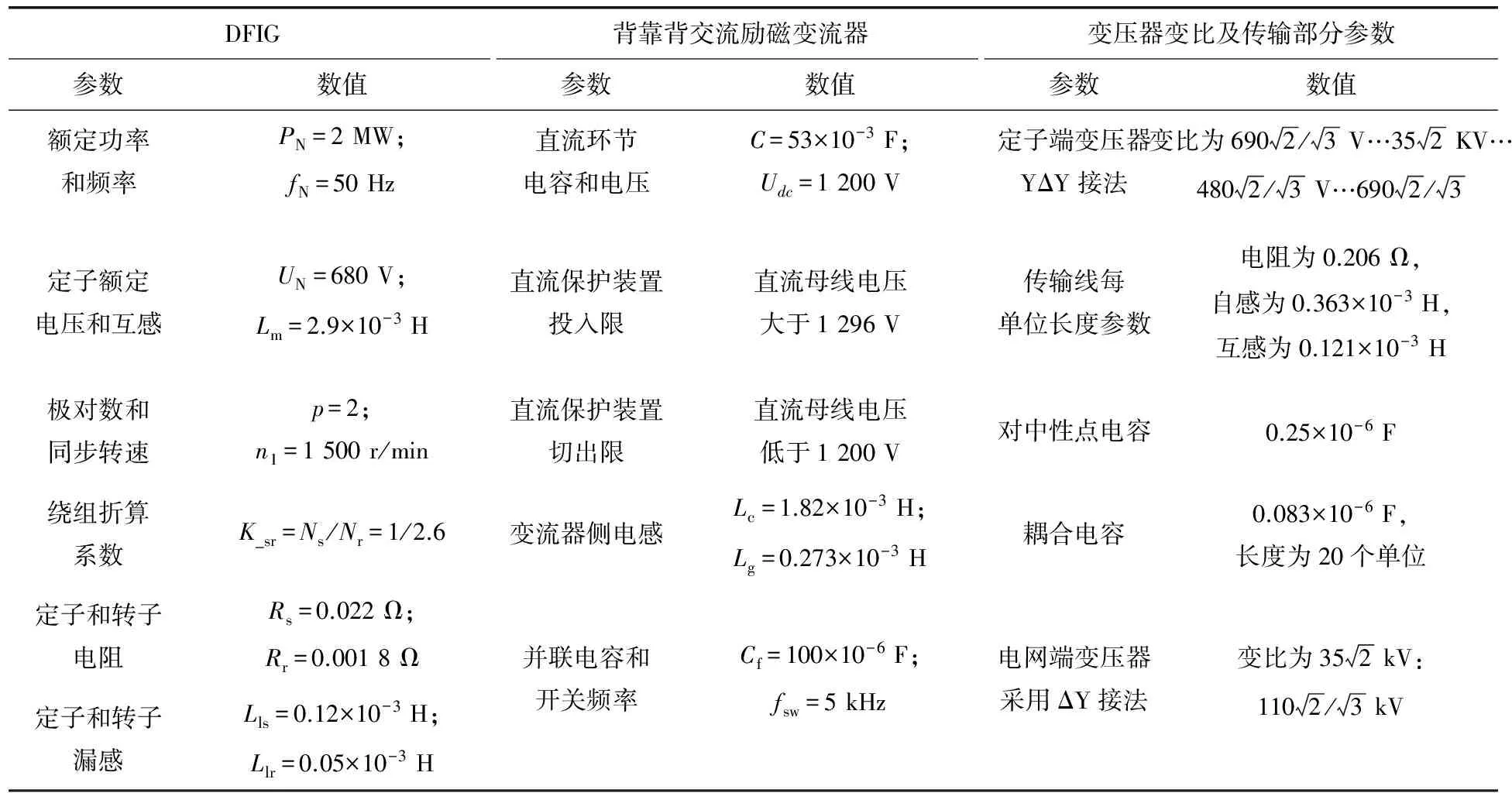
表1 双馈异步风力发电系统的仿真试验参数

图3 DFIG运行在传统控制的次同步状态下，电网电压2%稳态不平衡度仿真结果

4. 1 电网电压瞬态跌落故障情况验证

图3和图4所示为在次同步运行时，采用传统和改进矢量控制方案条件下，发电机运行在转速为1 350 r/min的次同步状态，A相电压跌落6%(2%不平衡度)，并一直持续的仿真结果。

从图3可知，由于不平衡电压所产生的负序分量，转子电压与电流都出现了明显的畸变，定子电压与电流畸变率均接近于零，但是定子电流各相存在不同的直流偏置。转子角速度出现了0.029 rad/s(0.277 r/min)的稳态波动。定子有功功率振荡误差幅值达到0.145×106W，转子有功功率振荡幅值达到9×103W，定子无功功率振荡误差幅值达到2×105W，转子无功功率振荡很小。电磁转矩脉动幅值达到了0.12×104N·m。因此，在电网电压2%稳态不平衡度时，转子电流和电压畸变严重，定、转子功率振荡较大，电磁转矩脉动大，增加了传动系统的机械损耗。

图4所示为在采用改进矢量控制方案条件下，次同步运行时，电网电压出现2%稳态不平度的仿真波形。转子电压与电流畸变明显减小，转子角速度在0.01 rad/s仅有少量波动。定子有功功率振荡误差降低0.08×106W，占稳态值的0.2%，转子有功功率振荡幅值降低0.4×103W，占稳态值的0.118%，定子无功功率振荡误差幅值仅为0.5×103W，转子无功功率振荡很小。电磁转矩脉动幅值降低到0.75×102N·m，占稳态值的0.54%。

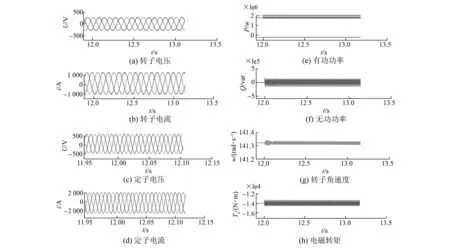
图4 DFIG运行在改进SVO控制的次同步状态下，电网电压2%稳态不平衡度仿真结果

4. 2 电网电压谐波下DFIG运行情况验证

图5和6为在转速1 650 r/min的超同步状态，采用传统和改进矢量控制方案条件下，电网电压中出现3%的5次谐波和2%的7次谐波的仿真结果如图5、图6所示。

图5中转子和定子电压、电流都出现畸变，定子电流总谐波畸变率THDi=4.07%，定子电压总谐波畸变率THDv=3.06%。转子角速度出现了0.020 rad/s(0.191 r/min)的稳态波动，定子有功功率振荡误差达到0.11×106W，转子有功功率振荡达到8×103W，定子无功功率振荡误差幅值达到1.2×105var。电磁转矩脉动幅值达到了0.063×104N·m。图5表明超同步运行时的定子电流畸变率较大，导致输出电能质量较差，加大了传动系统的机械损耗。

从图6可看出，电网电压包含谐波时，转子、定子电压与电流畸变也明显减少，定子电流总谐波畸变率THDi=1.91%，定子电压总谐波畸变率THDv=1.21%。转子角速度在0.015 rad/s(0.143 r/min)仅有微量波动，定子有功功率振荡误差幅值降低到0.08×104W，占稳态值的0.26%，转子有功功率振荡幅值最高为0.7×103W，占稳态值的0.295%，定子无功功率振荡误差幅值降低到0.11×104var，转子无功功率振荡小。电磁转矩脉动幅值仅为0.05×103N·m，占稳态值的0.48%。

通过图5与图6对比可知，提出的控制策略对于谐波的抑制效果明显，输出定子电压与电流的总谐波畸变率均较传统控制方法低，且功率与电磁转矩的振荡也能得到有效抑制。

图5 DFIG运行在传统控制的超同步状态下，电网电压含大量谐波时的仿真结果

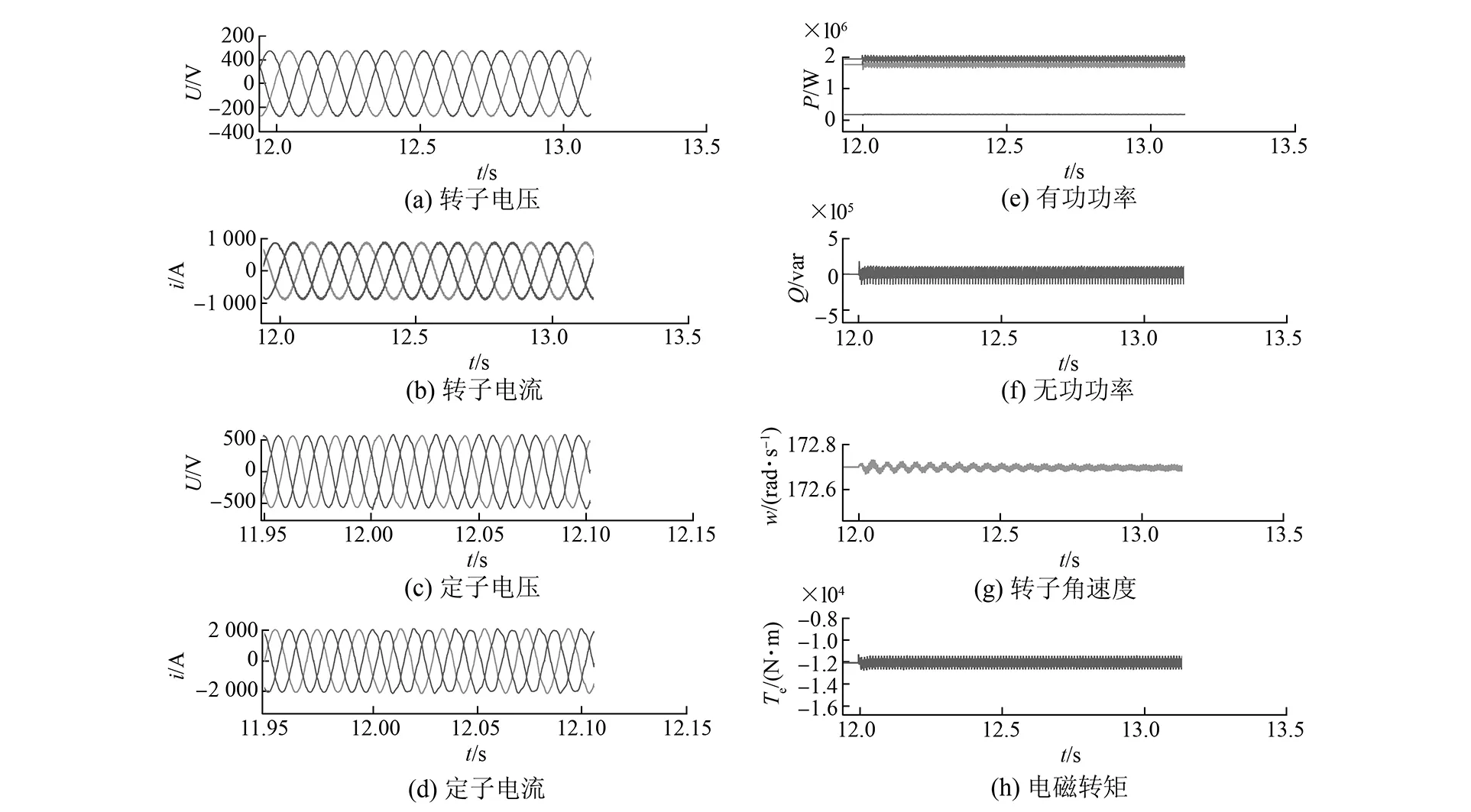
图6 DFIG运行在改进SVO控制的次超同步状态下，电网电压含大量谐波时的仿真结果

5 结 语

本文首先通过分析双馈机组数学模型结构，并且根据风电与电网功率交换形式，提出了一种基于SVO的定子磁链动态过程改进控制方案以及优化的最大功率跟踪策略，通过引入积分环节，消除电压故障状态产生的静差，再通过自适应调节补偿定子电阻，联合优化的最大功率跟踪器，增强风电机组供电质量，提高系统的鲁棒性。

最后在PLECS环境下搭建了风电交流微电网仿真模型，在电网电压瞬态跌落故障，以及含有大量电网谐波工况下分析，通过次同步和超同步下对传统控制策略及改进自适应控制方法对比分析，证明了提出的基于SVO的定子磁链动态过程改进控制方案可有效实现谐波抑制，减小定、转子功率振荡，电磁转矩脉动及传动系统的机械损耗，并为接下来在高渗透率风电场下的研究提供技术支撑。

[1] SHAYESTEH E, HOBBS B F, SODER L, et al. ATC-based system reduction for planning power systems with correlated wind and loads[J]. IEEE Transactions on Power Systems, 2015, 30(1): 429-438.

[2] 李兢,乔颖,王彩霞,等.大规模风电并网对CPS指标的影响[J].南方电网技术,2014,8(6): 98-103.

[3] FERNANDEZ L M, JURADO F, SAENZ J R. Aggregated dynamic model for wind farms with doubly fed induction generator wind turbines[J]. Renewable Energy, 2008, 33(1): 129-140.

[4] 肖帅,杨耕,耿华.抑制载荷的大型风电机组滑模变桨距控制[J].中国电工技术学报,2013,28(7): 145-150.

[5] RAMTEEN S, WALTER S. Evaluating the impacts of real-time pricing on the usage of wind generation[J]. IEEE Transactions on Power Systems, 2009, 24(2): 516-524.

[6] ZHONG H, XIE L, XIA Q. Coupon incentive-based demand response: Theory and case study[J]. IEEE Transactions on Power System, 2013, 28(2): 1266-1276.

[7] 杨楠,王波,刘涤尘,等.计及大规模风电和柔性负荷的电力系统供需侧联合随机调度方法[J].电机工程学报,2013,33(26): 63-69.

[8] 林俐,李晓钰,王世谦,等.基于分段控制的双馈风电机组有功-频率控制[J].中国电力,2012,45(2): 49-53.

[9] 贺益康,徐海亮.双馈风电机组电网适应性问题及其谐振控制解决方案[J].中国电机工程学报,2014,34(29): 5188-5203.

[10] 张建设,李浩,黄家栋,等.双馈式风力发电系统实时数字仿真研究[J].南方电网技术,2014,8(6): 104-108.

Optimal Operation Strategy of Doubly Fed Induction Generator Based on Stator Voltage-Oriented Adaptive Controller Under Grid Fault*

LUChang,WUZhenyu,HUJuntai,FUXiao

(Pingdingshan Power Supply Company, State Grid Henan Power Company, Pingdingshan 467001, China)

An improved stator voltage oriented (SVO) control strategy of wind turbine control based on doubly fed induction generator (DFIG) was presented. An extra integral controller was utilized into the SVO to clean the static deviation under disturbance of grid voltage. Combining with the controller of maximum power tracking, the quality of power supply of wind turbines was enhanced, and the stability and robustness of the system were improved. The PLECS-based simulation results had showed that the suppression of harmonic voltage was realized and power oscillation was largely reduced by the improved control method. Furthermore, the proposed control strategy could be utilized to further provide the basis for the research on wind farm with high permeability.

stator voltage oriented (SVO); power quality; maximum power point tracking (MPPT); doubly fed induction generator (DFIG); transient drop; harmonic voltage

国网河南省电力公司平顶山供电公司科技项目资助(SGHAPD00JYJS1500490)

陆 畅(1980—)，男，高级工程师，研究方向为电力系统运行与控制。

TM 301.2

A

1673-6540(2017)04- 0093- 08

2016 -10 -21