永磁同步电机调速系统新型模型预测控制

徐 楠, 吕 彦, 谢后晴

(中国矿业大学 信息与电气工程学院,江苏 徐州 221008)

永磁同步电机调速系统新型模型预测控制

徐 楠, 吕 彦, 谢后晴

(中国矿业大学 信息与电气工程学院,江苏 徐州 221008)

传统PI控制器在指令信号及负载发生变化时不能很好地兼顾系统响应的快速性与稳定性。为解决该问题，将模型预测控制用于调速系统电流内环的设计，从而可获得较传统PI控制更小的电流纹波。速度外环采用指数趋近律设计速度滑模控制器来替代传统的PI控制器。由于速度环采用滑模变结构控制，可使得系统在具备较快电流响应速度的基础上，速度抗扰性能也得到改善。最后对该方法进行仿真与试验验证，证明了该方法的可行性与有效性。

永磁同步电机;模型预测控制;滑模变结构控制;指数趋近律

0 引 言

永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)由于具有结构简单、转动惯量小、效率高和控制性能好等优点，被广泛应用于中小功率交流调速系统[1-3]。目前大多数的PMSM调速系统，电流内环与速度外环均采用PI控制。该种控制简单易行，但由于是线性调节器且存在积分饱和、系统约束不好处理的问题，限制了系统的动态响应能力和抗干扰性能，制约了其在高性能控制场合的应用[4-7]。

为了改善PMSM调速系统的控制性能，国内、外学者提出了多种新型的控制方法，如滑模变结构控制、模糊控制、自适应控制、反馈线性化控制及模型预测控制(Model Predictive Control,MPC)等[8-12]。其中MPC通过对系统未来状态的预测，可求解出系统的最优控制量，被广泛应用于交流调速场合[13]。当前MPC在PMSM调速系统多用于电流环的设计，以求获得较好的电流响应特性[14]。文献[15-16]研究了改进电流预测控制，只用一个电机参数，有效降低了对模型参数准确性的依赖。文献[17]提出一种用于表贴式PMSM模型预测电流控制算法，通过电流前馈和反馈控制实现了dq轴电流的有效解耦，改善了电流控制的动态性能。上述几种模型控制方法只针对电流内环进行，但速度外环仍采用PI调节器，故速度抗扰性并未得到优化。

本文为了提高PMSM调速系统的动态品质，结合滑模变结构理论，提出采用指数趋近律设计速度控制器来替代原有的线性PI控制器，采用MPC设计系统的电流环控制器。通过滑模变结构与MPC的结合，可获得很好的电流特性，且可提高速度环的抗扰性。最后，对控制器进行了仿真与试验验证，结果表明,相比传统的PI控制，该方法控制下的系统具有更小的电流谐波、更好的抗负载扰动性能及更快的速度动态调节性能。

1 PMSM数学模型

在忽略定转子铁心磁阻，不计铁心损耗，假设转子上没有阻尼绕组，永磁体无阻尼作用,同时各相绕组感应电动势为正弦波的条件下，PMSM在dq两相旋转坐标系下的数学模型如下所示[18]：

(1)

(2)

(3)

(4)

式中:id、iq——d、q轴电流；Ld、Lq——d、q轴电感；Rs——定子电阻；ωr——转子电角度；ud、uq——d、q轴电压；ψf——永磁体与定子交链的磁链;J——电机转动惯量；p——电机极对数；Te——电机电磁转矩；TL——负载转矩。

2 电流环的设计

采用MPC设计电流环时需要对式(1)所示的电机电流模型进行离散化处理，设采样时间为Ts，采用前向欧拉法可得到dq参考坐标系下的预测定子电流表达式：

(5)

对电流环而言，期望达到以下控制目标：

(1) 转矩电流参考跟踪(id=0控制)；

(2) 转矩/安培的比值优化；

(3) 电流幅值限制。

上述控制目标可以通过式(6)所示的代价函数实现：

(6)

其中：

(7)

电流环的控制过程是利用式(5)所示的预测模型来预测逆变器产生的7个不同电压矢量所分别对应的定子电流，根据预测得到的这7种电流，选择能够使得式(6)值最小的一组电流所对应的电压矢量，并将其用于下一采样时刻，至此完成对电流环的有效控制。

3 速度环设计

3. 1 滑模速度控制器设计

取PMSM状态变量为[19]

(8)

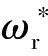
由于采用id=0控制，故转矩方程可写为

(9)

结合式(4)、式(8)与式(9)可得

(10)

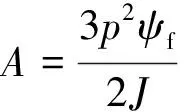
(11)

将滑模面设为s=cx1+x2，对其求偏导得

(12)

又已知指数趋近律如式(13)所示。

(13)

其中：k>0;ε>0。

结合式(11)～式(13)可求解得到

(14)

对式(14)进行离散化处理，设采样时间Tsw=10Ts，即为电流内环的10倍，可得到滑模速度控制器的输出为

(15)

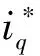
3. 2 稳定性分析

选取Lyapunov函数为V=(ss)/2，由Lyapunov稳定性理论可知，当式(16)成立时，即满足滑模到达条件[20]。

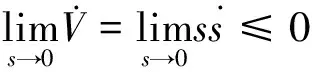
(16)

将式(13)代入式(16)得

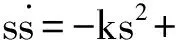
(17)

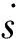
当系统进入滑动模态后，结合公式s=cx1+x2可获得系统运动的微分方程

(18)

可解得

(19)

式中：c0——常数，这表明进入滑动模态后速度误差x1会无限接近于0，从而实现转速无超调跟踪。

4 仿真与试验验证

4. 1 仿真研究

PMSMMPC系统框图如图1所示。

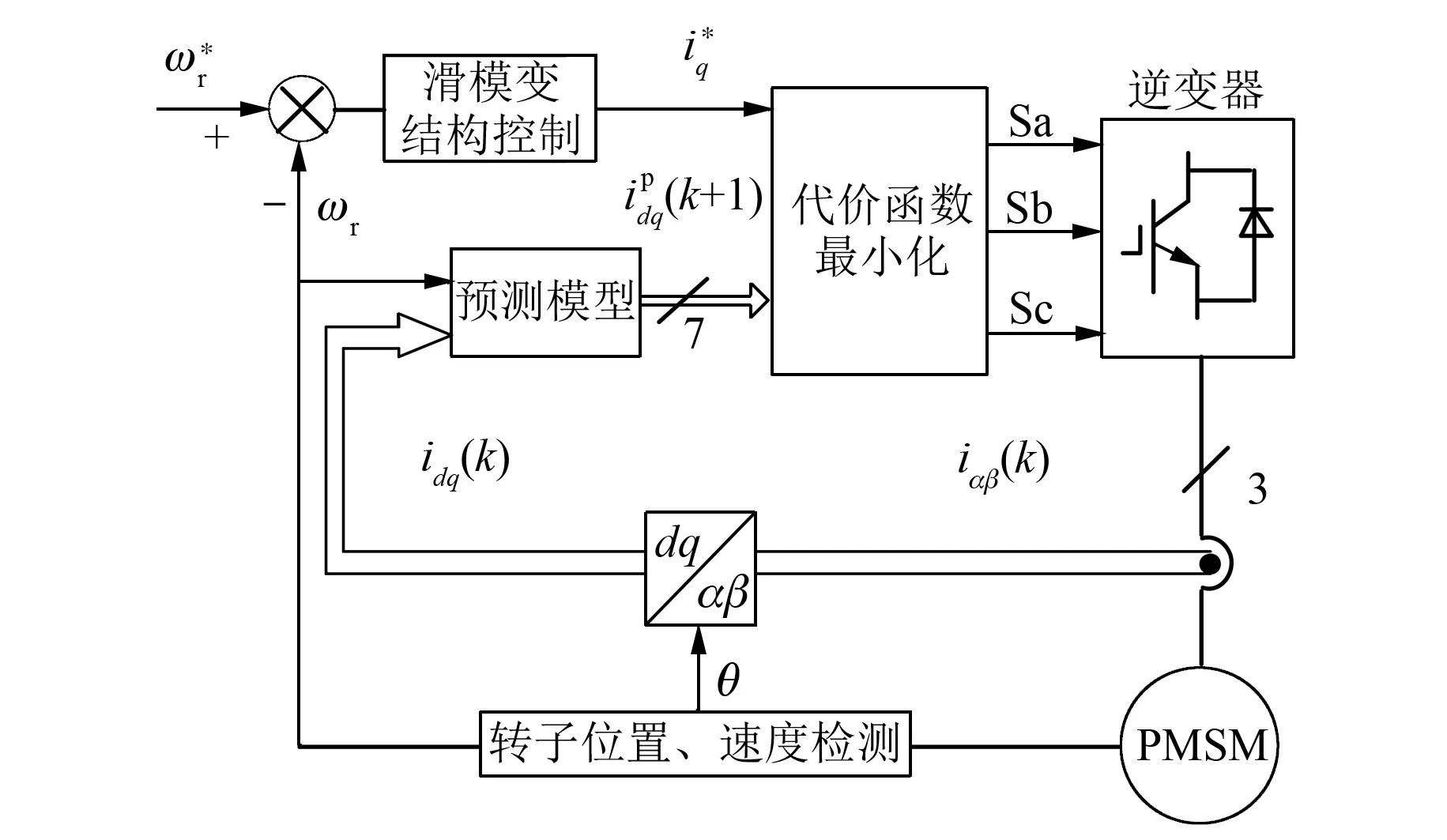
图1 PMSM速度预测控制系统框图

根据图1建立MATLAB/Simulink仿真模型。仿真中电机参数设定参照表1所示电机实际参数。

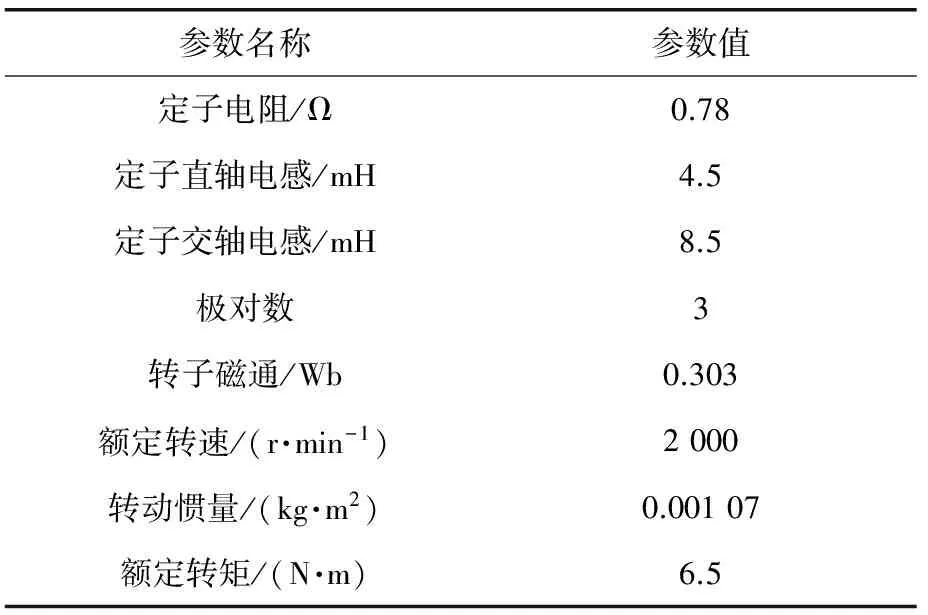
表1 PMSM参数

对双闭环PI控制与本文所提出的新型MPC两种控制方法分别进行了增减速与加减载仿真验证。

(1) 增减速仿真验证。仿真条件：给定转速为100 rad/s，电机带2 N·m负载起动，0.25 s时给定速度增至200 rad/s，0.35 s时减至50 rad/s。

图2(a)与图2(b)分别为PI控制与MPC下的速度响应。从图2可以看出，这两种控制都能有效地跟踪速度给定值，在速度给定值发生变化时能快速到达给定。但PI控制下的系统在起动时速度有超调，超调量为3%，而本文提出的控制方法，由于速度环采用滑模变结构控制，实现了速度起动无超调。

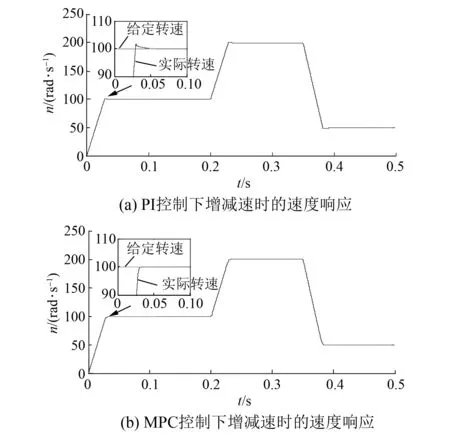
图2 PI控制与MPC下的速度响应

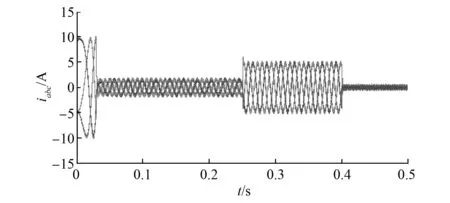
图3 PI控制加减载时定子三相电流

图4 MPC加减载时定子三相电流

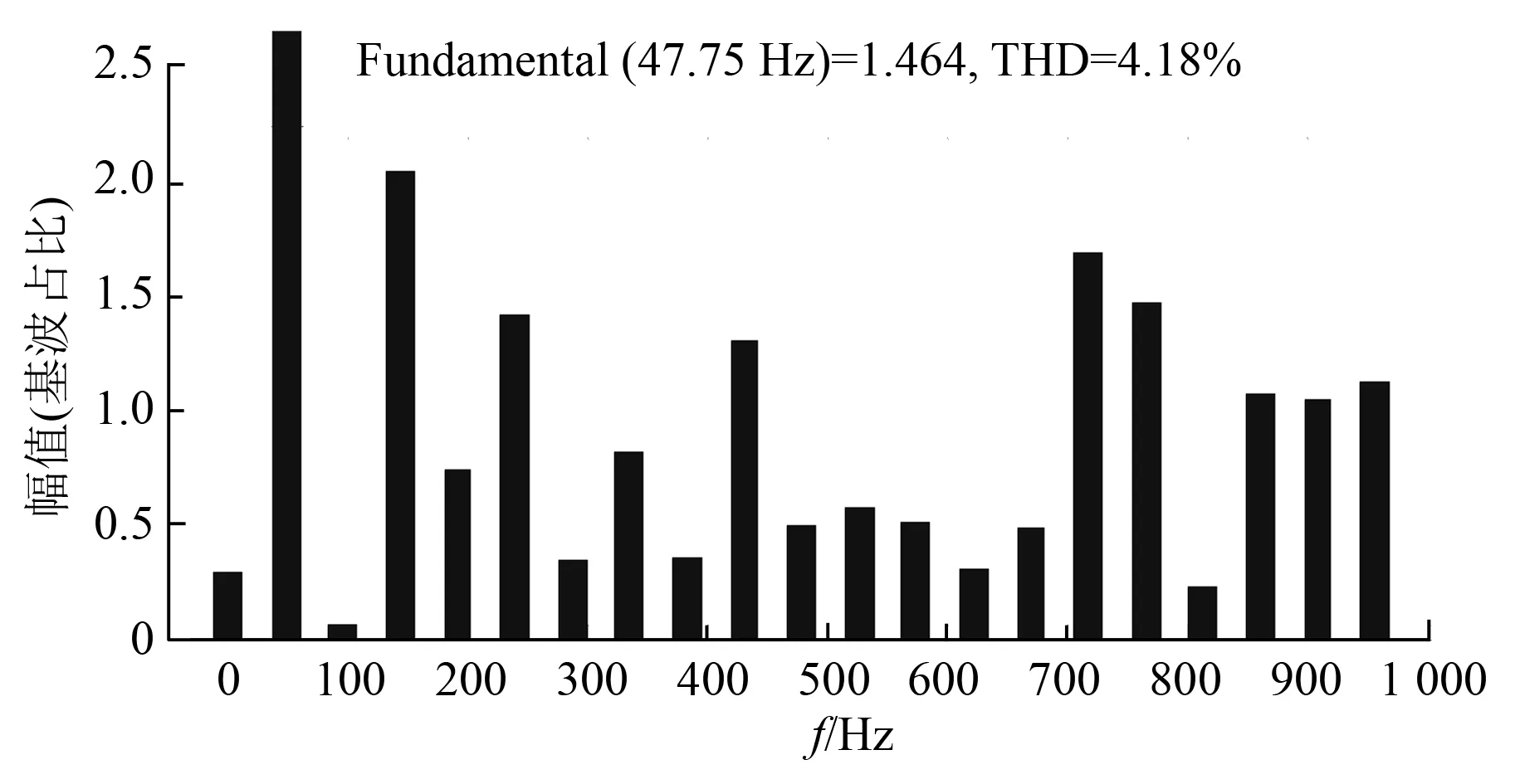
图5 PI控制下定子电流谐波分析图

图6 MPC下定子电流谐波分析图

(2) 加减载仿真验证。仿真条件：给定转速为100 rad/s，电机带2 N·m起动，0.25 s后加载至额定负载，0.4 s切除负载。

图3与图4分别为两种控制方法下的定子三相电流响应图。图5与图6分别为两种控制方法下定子电流的谐波分析图。分析图3～图6可知，双PI控制下的系统定子三相电流谐波含量较大，为18.47%。本文所提出的控制方法由于电流环采用预测电流控制，可有效降低电流纹波，因此该方法控制下的系统定子三相电流谐波含量很小，仅为4.18%。

图7 PI控制下加减载时电机转矩响应

相应的两种控制方法下的电机输出转矩脉动情况也有较大差距。从图7与图8可知，PI控制时，转矩脉动较大，新型MPC下的转矩脉动很小，相较PI控制稳定性得到提高。

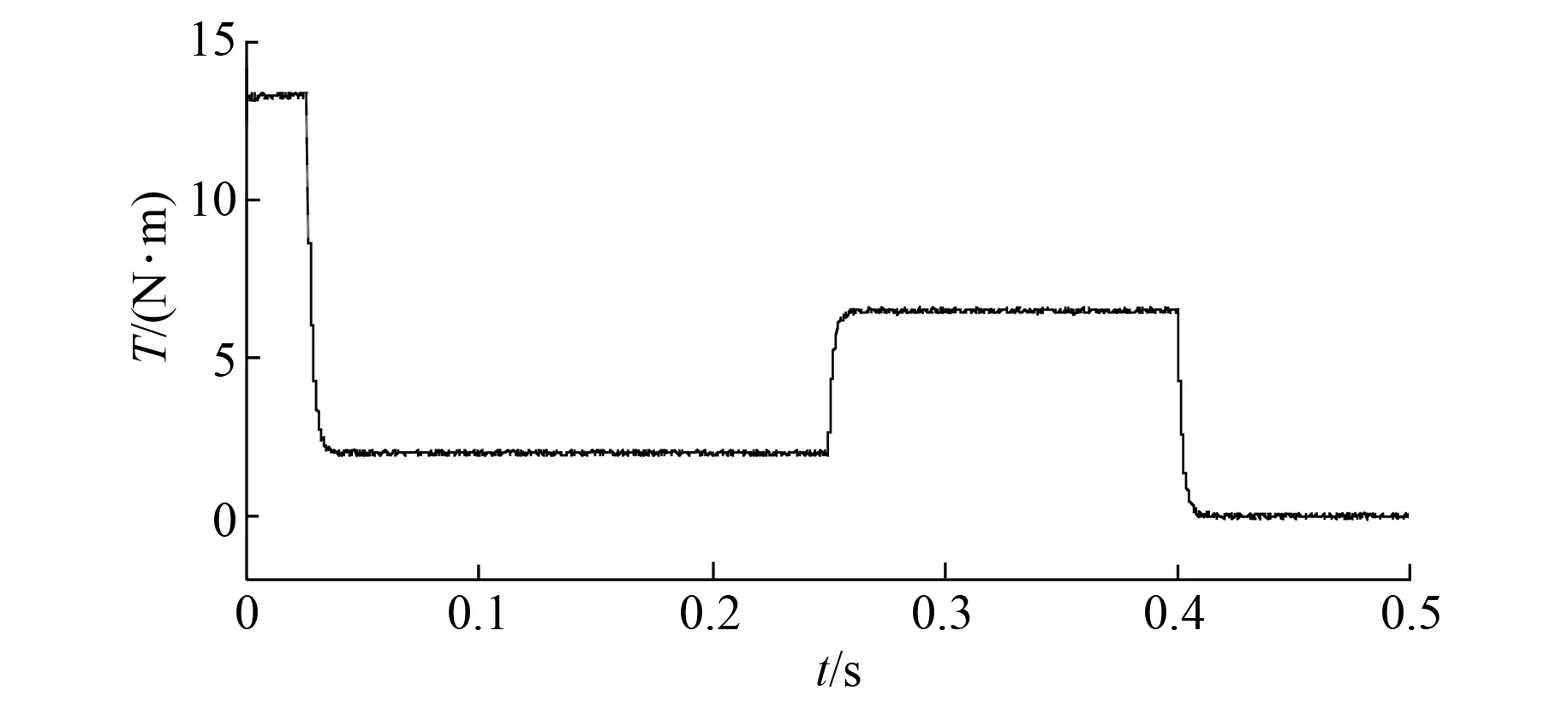
图8 MPC下加减载时电机转矩响应

图9与图10为变载时速度响应放大图。从图9～图10可知，PI控制下的系统转速动态调节时间长，变载时转速波动较大。新型MPC下的系统在变载时速度波动很小，转速经过很短的时间便恢复到给定值。这说明本文提出的控制方法可很好地改善系统的抗负载干扰能力。

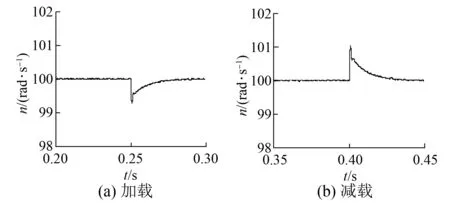
图9 PI控制下增减载时的速度响应

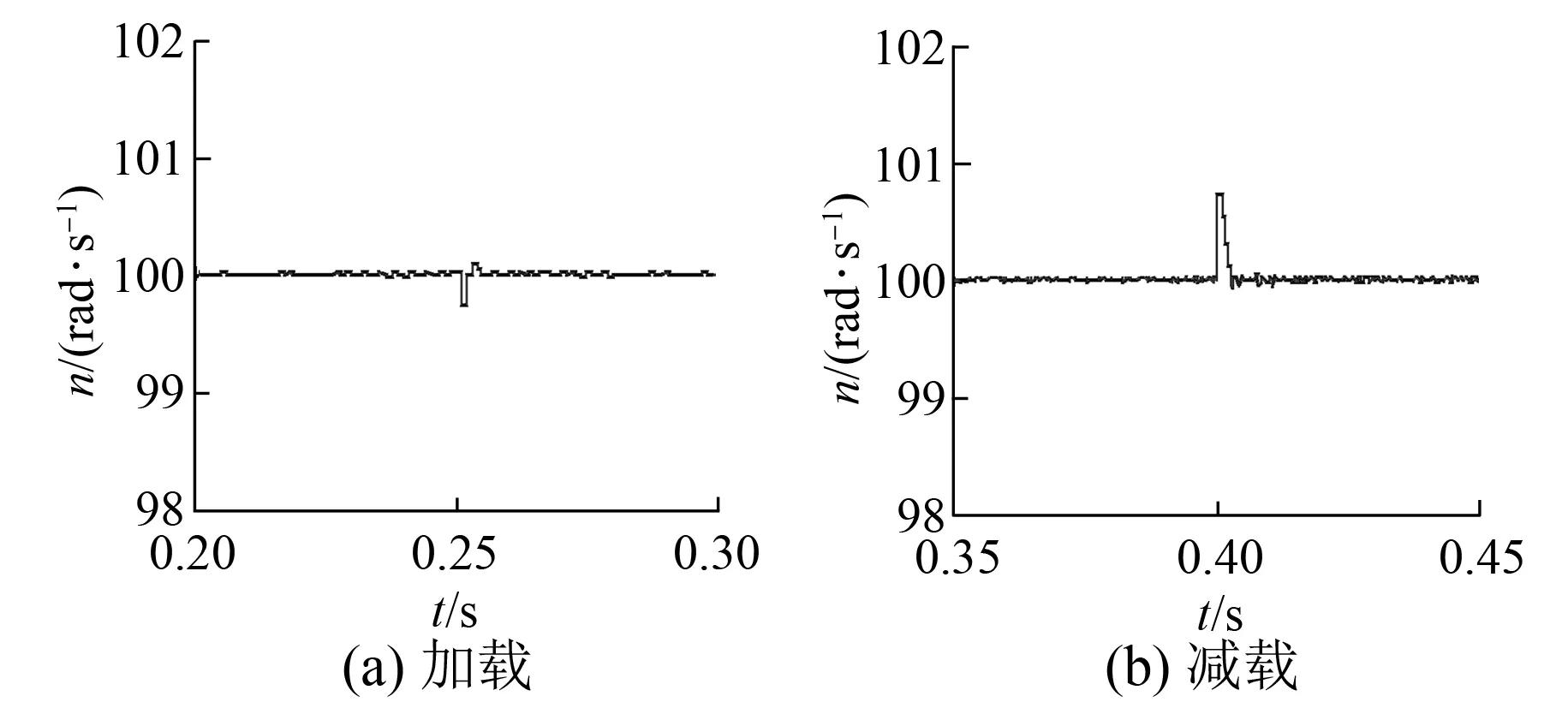
图10 MPC下增减载时的速度响应

4. 2 试验验证

试验平台由基于TMS320F28335的两电平逆变器和一套1.36 kW的内置式PMSM系统组成。试验主要测试新型模型预测系统在空载起动和变载时的动态特性，试验平台如图11所示。

图11 试验平台

图12与图13分别为给定转速400 r/min，电机在两种不同控制方法下的空载起动波形。从图12～图13可知，PI控制下的系统起动不平稳，这是PI控制器的积分饱和导致积分作用不强的原因，且起动时也存在超调问题。MPC下的电机实现了转速无超调起动。

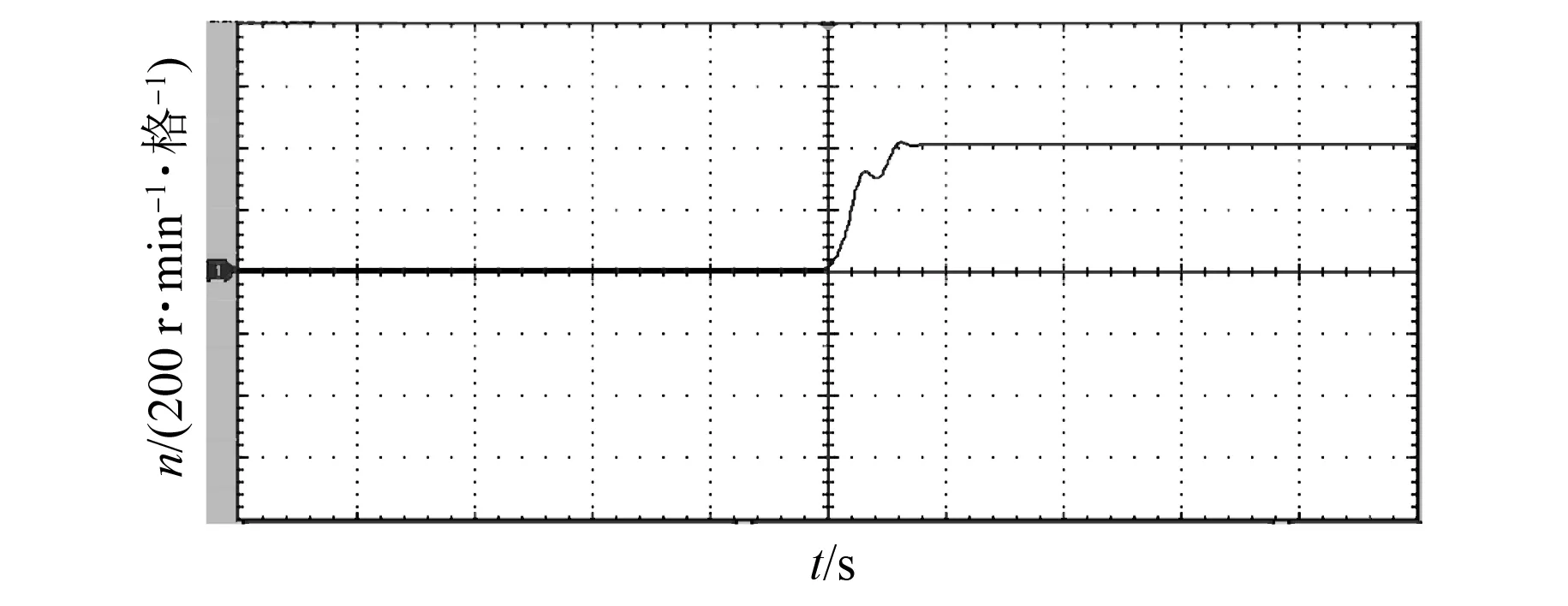
图12 PI控制下空载起动速度波形

图13 MPC控制下空载起动速度波形

图14与图15分别为给定速度400 r/min，负载增加时的转速响应与q轴电流响应。

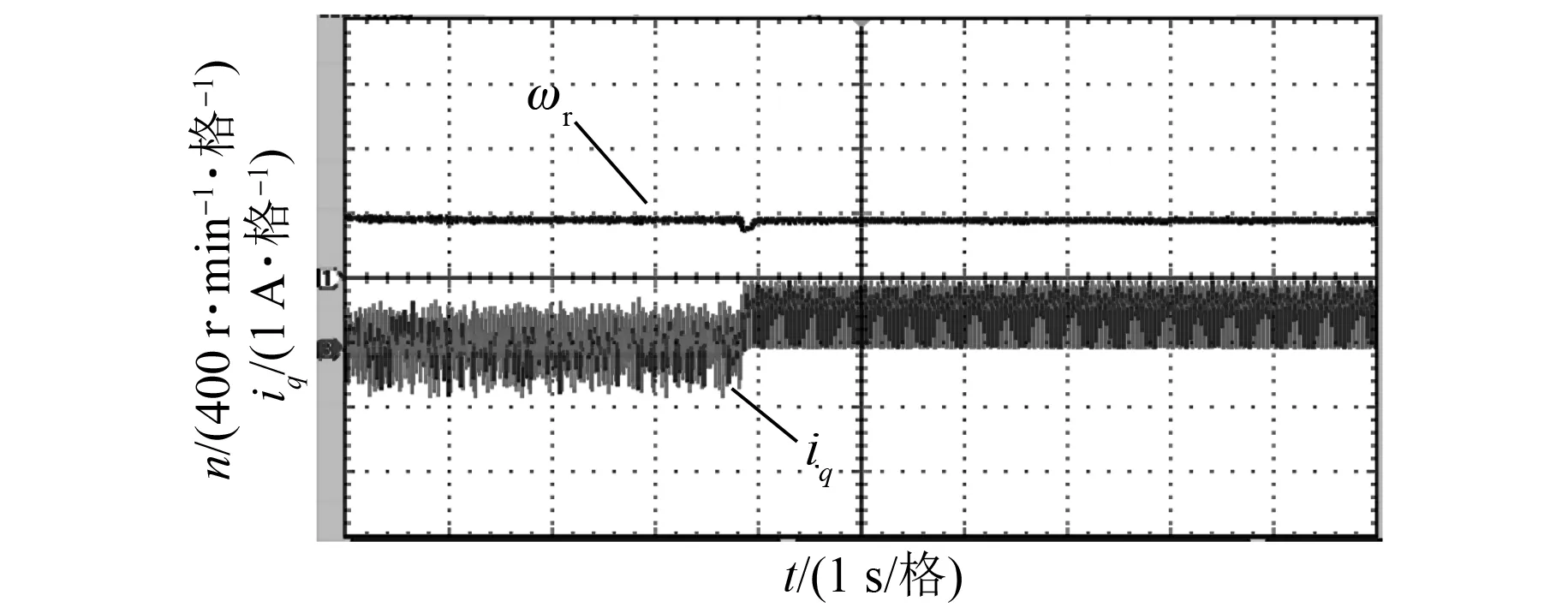
图14 PI控制下加载时速度与q轴电流响应

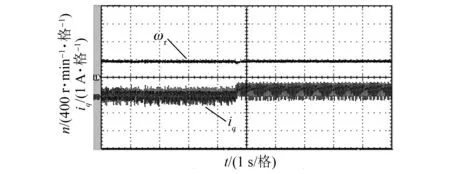
图15 MPC加载时速度与q轴电流响应

由图14和图15可知，在加载时PI控制下的系统转速跌落值较大，而MPC下转速在加载时几乎未受到影响，跌落很小。这证明新型控制方法下的系统有很好的抗干扰能力。

5 结 语

针对传统PI控制的PMSM调速系统存在抗干扰能力差、不能同时兼顾系统响应的快速性与稳定性的要求，提出了一种新型MPC方法。该方法结合了滑模变结构控制与MPC，可以改善电流环的谐波特性，同时提高速度环的抗干扰性能。

[1] 李崇坚.交流同步电机调速系统[M].北京: 科学出版社,2013.

[2] 唐任远.现代永磁电机理论与设计[M].北京: 机械工业出版社,1997.

[3] 陈荣.永磁同步电机控制系统[M].北京: 中国水利水电出版社,2009.

[4] 王伟华,肖曦,丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报,2013,28(3):50-55.

[5] 符慧,左月飞,刘闯,等.永磁同步电机转速环的一种变结构PI控制器[J].电工技术学报,2015,30(12): 237-242.

[6] 郭新华,温旭辉,赵峰,等.基于电磁转矩反馈补偿的永磁同步电机新型IP速度控制器[J].中国电机工程学报,2010,30(27): 7-13.

[7] 孙强,程明,周鹗,等.新型双凸极永磁同步电机调速系统的变参数PI控制[J].中国电机工程学报,2003,23(6): 117-123.

[8] 张晓光,赵克,孙力,等.永磁同步电动机滑模变结构调速系统新型趋近率控制[J].中国电机工程学报,2011,31(24): 77-82.

[9] 刘军,刘丁,吴浦升,等.基于模糊控制调节电压矢量作用时间策略的永磁同步电机直接转矩控制仿真研究[J].中国电机工程学报,2004,24(10): 148-152.

[10] 鲁文其,胡育文,梁骄雁,等.永磁同步电机伺服系统抗扰动自适应控制[J].中国电机工程学报,2011,31(3): 75-81.

[11] 刘栋良,赵光宙.基于直接反馈线性化的永磁同步电机速度跟踪控制[J].电气传动和自动控制,2006,28(2): 8-10.

[12] FUENTES E, RODRIGUEZ J, SILVA C, et al. Speed control of a permanent magnet synchronous motor using predictive current control[C]∥ IEEE 6th International Power Electronics and Motion Control Conference, IPEMC’09, 2009: 390-395.

[13] 何凤有,王从刚,曹晓冬,等.感应电机准无差拍模型预测电流控制策略[J].电机与控制学报,2013,17(9): 57-63.

[14] MOREL F, SHI X L, RETIF J M, et al. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2715-2728.

[15] 牛里,杨明,刘可述,等.永磁同步电机电流预测控制算法[J].中国电机工程学报,2012,32(6): 131-137.

[16] 王宏佳,徐殿国,杨明.永磁同步电机改进无差拍电流预测控制[J].电工技术学报,2011,26(6): 39-45.

[17] 王东文,李崇坚,吴尧,等.永磁同步电机的模型预测电流控制器研究[J].电工技术学报,2014,(s1): 73-79.

[18] 杨国良,李建雄.永磁同步电机控制技术[M].北京: 知识产权出版社,2015.

[19] 汪海波,周波,方斯琛.永磁同步电机调速系统的滑模控制[J].电工技术学报.2009,24(9): 71-77.

[20] 高为炳.变结构控制理论基础[M].北京: 中国科学技术出版社,1990.

Speed Control of Permanent Magnet Synchronous Motor Using Novel Model Predictive Control

XUNan,LÜYan,XIEHouqing

(School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou 221008, China)

The conventional PI controller has a bad performance when the command signal or the load changes. To solve the problem, the model predictive control was proposed to design the inner current loop of the speed control system, which could reduce the current ripple compared with the PI controller. The outer speed loop utilized the sliding mode controller based on the exponent reaching law to replace the PI controller, which could improve the robust of speed loop. Finally, simulations and experiments were done to verify the method. The results showed that the method was feasible and effective.

permanent magnet synchronous motor (PMSM); model predictive control (MPC); sliding mode control; exponent reaching law

徐 楠(1992—)，女，硕士研究生，研究方向为永磁同步电机传动控制系统。

TM 301.2

A

1673-6540(2017)04- 0064- 06

2016 -07 -09