DS － CDMA 信号盲分离自适应算法研究

吴 麒

(中国西南电子技术研究所，四川 成都 610036)

DS － CDMA 信号盲分离自适应算法研究

吴 麒

(中国西南电子技术研究所，四川 成都 610036)

对于DS-CDMA通信系统而言，对不同用户的信号进行分离是十分困难的.盲信号分离算法是解决该问题的重要手段之一.分析了基于LMS/RLS/Kalman滤波/APA的DS-CDMA信号盲分离自适应算法的原理，并仿真比较了上述盲分离自适应算法的性能.计算结果表明APA算法在误码率及信干比方面具有优势.

直接序列码分多址; 通信侦察; 盲分离; 误码率

直接序列码分多址(DS-CDMA)技术因为具备抗多径、抗干扰、功率谱密度低、低截获概率、多址复用等优点，被广泛应用于军事通信、卫星通信、移动通信等各个方面.对于DS-CDMA系统而言，不同信号在同一时间使用同频信道，仅通过不同的地址码来进行区分和检测，故仅使用频率等信息对不同信号进行分离是十分困难的.如果可以对非合作DS-CDMA系统不同用户信号实现有效盲分离，就可以为实现对敌方DS-CDMA系统用户信息的非合作解调奠定基础.因此，对适用于非合作DS-CDMA信号的盲分离算法进行研究具有十分重大的意义.

传统的DS-CDMA系统信号分离技术[1,2]需要了解所有用户信号的特征波形、扩频码以及定时等先验知识，以实现对单个信号的准确检测和分离.然而在通信侦察中，无法事先知道非合作通信方的上述先验知识，从而导致这些方法在实际应用中受到极大的约束和限制.在此背景下，适用于非合作DS-CDMA系统不同信号的盲分离自适应算法应运而生.只要获取到目标信号的观测数据，该算法就可以在不需要知道其他所有信号的扩频码情况下，甚至不用进行信道估计，就可以估计出目标信号的发送数据.

在盲分离自适应技术中，LMS算法[3]、RLS算法[3]、Kalman滤波算法[4,5]以及APA算法[6]等为常用算法.本文分析了上述算法的原理，并针对非合作DS-CDMA系统进行建模，然后仿真比较这些算法的性能.

1 问题描述

假定目前非合作方正在实施通信过程，其使用的通信系统为拥有K个用户信号的直接序列码分多址(DS-CDMA)系统，发射机信号全部通过加性高斯白噪声无线信道到达接收机.在通过码片滤波及速率采样处理后，接收机输出的可用信号模型[7，8]如下：

(1)

上式中V(n)表示为信道噪声；Ak为第k个信号的接受幅度值；bk(n)表示为第k个信号的接受信息字符序列；Sk(n)表示为第k个信号特征波形信息；σ为一常数.假定各个信号的bk(n)将从{-1,+1}中随机选取，且Sk(n)具备单位能量，即：

且特征波形的支撑区间为[0,Ts]，其中Ts(Ts=NTc)表示码元间隔，而N表示扩频码增益参数，Tc表示码片间隔信息[1,7].

基于以上定义，可以将盲分离自适应问题描述如下：假设目前已知的一个码元间隔内的接收信号表示为Y(0),…,Y(N-1)，且与之对应的期望信号特征波形表示为Sd(0),…,Sd(N-1)，而bd(0),…,bd(N-1)为对应的期望信号发射的信息字符.为方便起见，假定用户信号1是我们感兴趣的非合作方目标信号，定义接收信号向量和噪声向量如下：

定义用户信号k的特征波形向量为

sk=[Sk(0),Sk(1),…,Sk(N-1)]T

根据以上假设，公式(1)可以表示成如下形式：

上式中第一项为非合作方目标信号，第二项为对其他所有干扰信号进行求和，第三项表示为信道噪声.

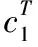
对于盲多信号分离器c1，有如下两种典范表示：

a)典范表示1：c1(n)=s1+x1(n)

b)典范表示2：c1(n)=s1-C1,nullw1

从以上典范可以看出，盲多信号分离器由固定部分s1与自适应部分组成，且这两部分为正交关系，即：

〈s1,x1〉=〈s1,C1,nullw1〉=0

对于典范1，约束条件可以等价的表示为：

〈c1,s1〉=〈s1,s1〉=1

由于〈c1,s1〉=1，故称c1(n)是一个规范化的盲信号分离器.在下一节中，我们可以知道基于LMS、RLS的盲多信号分离算法是根据典范1推导出来的，而基于Kalman滤波的盲信号分离算法是根据典范2推导出来的.

2 盲信号分离算法

2.1LMS算法

对于应用典范1描述的盲信号分离器c1(n)=s1+x1(n)，其输出信号〈c1,y〉的平均输出能量表示为MOE(c1)，其均方误差表示为MOE(c1)：

求平均输出能量关于c1(n)的无约束梯度，得

那么，盲信号分离器c1(n)的自适应部分x1(n)的随机梯度自适应算法为：

(2)

(3)

容易证明

(4)

这里使用了〈y,s1〉为标量和各信号特征波形具有单位能量即〈s1,s1〉=1这两个结果.式(4)可以等价为[y-〈y,s1〉s1]⊥s1，那么y中与s1正交的分量为y-〈y,s1〉s1.因此，由式(3)和式(4)可知，与s1正交的投影梯度为

2〈y,s1+x1〉[y-〈y,s1〉s1]

令s1和s1+x1(n-1)的匹配滤波器输出响应分别为：

ZMF(n)=〈y(n),s1〉

(5)

Z(n)=〈y(n),s1+x1(n-1)〉

(6)

将以上式(5)和式(6)代入式(2)得到如下的随机梯度自适应算法的更新公式：

在缺乏干扰信号特征波形先验知识的条件下，上述更新公式的初始条件可以设定为x1(0)=0.

因此，盲信号分离的LMS滤波算法如下所示：

在使用LMS算法时，步长μ必须满足输出均方误差收敛的稳定性条件：

其中，N为扩频增益，σ2为背景噪声.

2.2RLS算法

RLS算法的提出是依据使盲分离器的指数加权输出能量最小化，即：

其中，λ为遗忘因子，其值为0<λ<1.其作用为对离当前时刻较远的误差赋予较大的权重，而当前时刻较近的误差赋予较小的权重.考虑到〈s1,s1〉=1及〈s1,x1〉=0，容易验证约束条件与典范1的公式是等价的.因此，满足上述两个约束条件的最优分离器为：

令

表示观测信号的自相关矩阵.可以利用矩阵求逆引理[9]对R-1(n)进行更新，从而得到RLS算法如下：

2.3Kalman滤波算法

Kalman滤波算法是依据被提取信号相关的观测量估计出目标信号的一种滤波算法.Kalman滤波算法由Wiener滤波发展而来，其优点是其滤波算法是递推的，适于处理多变量、非平稳、时变系统状态，克服了Wiener滤波必须使用无限多历史数据从而不适用于实时处理的缺点.

对于一般的非平稳DS-CDMA系统，状态方程如下：

Wopt1(n+1)=F(n+1)Wopt1(n)

其中，Wopt1为最佳线性检测器的自适应部分，F(n+1,n)为描述系统在时间n到n+1的状态转移矩阵；对于平稳DS-CDMA系统，一般有Wopt1(n+1)=Wopt1(n)，即F(n+1,n)=I.在慢时变DS-CDMA系统中有

Wopt1(n+1)=Wopt1(n)+δWopt1(n)

且δWopt1(n)的元素都是非常小的量，所以可以认为慢时变DS-CDMA系统的状态方程为

Wopt1(n+1)≈Wopt1(n)

(7)

为得到观测方程，定义目标信号的测量误差向量：

(8)

把典范表示式c1(n)=s1-C1,nullw1代入式(8)有：

(9)

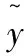
递推初始条件如下：

2.4APA算法

APA算法最小化权重矢量的欧式范数的平方，需要满足如下多个约束条件：

其中d(n)是期望响应，u(n)是输入数据矢量，L是数据块的维数，也称为APA自适应滤波器的阶次.

尽管对于诸如声学回声消除器的重要应用场合，APA算法可以直接应用，但是却不能直接应用到DS-CDMA系统，这主要是因为除了被用于目标信号的训练数据序列之外，d(n)是未知的.因此我们不能直接把APA算法应用到多信号分离中.为了改进APA算法以适应盲信号分离器的设计，即：

(10)

其中：

利用拉格朗日乘子法，设乘子为以下的一个向量：

λ=[λ1,λ2,…,λL+1]T

则拉格朗日函数可以定义为：

J(n)=‖c(n+1)-c(n)‖2+2λT[d-XT(n)c(n+1)]

令上式导数为零，即

则有

c(n+1)=c(n)+X(n)λ

(11)

将式(11)代入式(10)的约束条件

XT(n)c(n+1)=d

中，可以得到

λ=[XT(n)X(n)]-1[d-XT(n)c(n)]

基于上述讨论，APA算法的计算步骤如下所示：

2.5 算法复杂度

理论上LMS、RLS、APA和Kalman滤波四种自适应滤波算法的计算复杂度如表1所示.以上表格中，N表示扩频增益，L表示基于APA算法的滤波器的阶数.

表1 盲多信号分离算法计算复杂度

一般而言，N>L，因此APA算法要比RLS和Kalman滤波算法有更低的算法复杂度.

3 数值仿真

为了比较不同算法的盲信号分离性能，使用n步迭代的时间平均信干比(SIR)作为测度：

图1 盲多信号分离算法的信干比随迭代次数的变化曲线

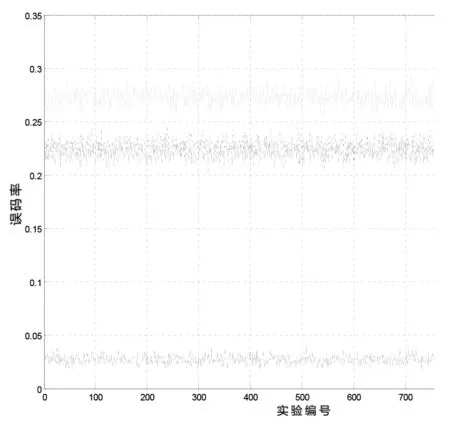
图2 盲多信号分离算法的误码率

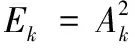
利用时间平均信干比与迭代次数的关系曲线来比较以上LMS、RLS、APA和Kalman滤波四种自适应滤波算法的分离性能和收敛速度.LMS滤波算法中的步长μ=3×10-4，RLS算法时，初始值R-1(0)=δ-1I，取δ=0.01，遗忘因子λ=0.997.APA算法的阶数L=4.

LMS、RLS、APA和Kalman滤波四种盲自适应多信号分离算法的SIR曲线如图1所示,误码率如图2所示.从图中可以得出，四种算法的收敛精度从高到低依次为APA算法、RLS算法、Kalman滤波算法以及LMS算法.另一方面，考察四种算法的收敛所需的迭代步数.LMS算法收敛步数大约是1000次左右，RLS算法需经600次左右的递推能收敛，而Kalman滤波算法的收敛步数进一步减少至500次；此外，APA算法的收敛速度不及上述三个算法，需经3000次递推才能收敛.

表1的理论结果与图1、图2的数值仿真结果表明，LMS算法的收敛速度很慢，同时它的性能依赖于接收数据的互相关矩阵的特征值分散；与LMS相比，RLS算法和Kalman滤波算法几乎在所有方面都表现出了更好的性能，但是需要很大的计算代价；而APA算法则在收敛速度和计算复杂度之间取得了一个很好的折中.

[1]栗书萍.在DS-CDMA系统中对盲多用户检测算法的研究[D].太原:太原理工大学硕士学位论文,2005.

[2]张贤达.现代信号处理[M].北京:清华大学出版社,2002.

[3]Honig M, Madhow U, Verdu S. Blind adaptive multiuser detection[J]. IEEE Trans on Information Theory,1995,(4):944-960.

[4]Zhang X, Wei W. Blind adaptive multiuser detection based on Kalman filtering [J]. IEEE Trans on Signal Processing, 2002,(1):87-95.

[5]高维廷,李辉.衰落信道下自适应卡尔曼异步IC多用户检测器[J].东北大学学报(自然科学版), 2014, (7):949-954.

[6]Li J, Zhang X. Blind adaptive multiuser detection based on affine projection algorithm[J].IEEE Signal Processing Letters, 2005, (10):673-676.

[7]史永超.第三代移动通信系统中基于子空间的盲自适应多用户检测技术研究[D].太原：太原理工大学硕士学位论文,2007.

[8]黄坤.直接序列扩频系统中多用户检测技术的研究[D].西安:西安电子科技大学硕士学位论文, 2014.

[9]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

(责任编校：晴川)

Research on Blind Signal Separating Adaptive Algorithm for CDMA System

WU Qi

(Southwest China Institute of Electronic Technology, Chengdu Sichuan 610036, China)

For DS-CDMA communication system, it is very difficult to separate the signals of different users. The blind signal separating algorithm is one of the most common techniques for solving the above problem. In this paper, we analyze the principles for some blind separating adaptive algorithms, i.e., the LMS algorithm, the RLS algorithm, the Kalman-filter base algorithm, and the APA algorithm. The simulation results show that the APA algorithm has a better BER and SINR performance than other algorithms.

DS-CDMA; communication reconnaissance; blind separation; bit error rate

2017-03-02

国防科技重点实验室基金(批准号：9140C020203150C02008)资助项目.

吴麒(1985— )，男，四川眉山人，中国西南电子技术研究所工程师，博士.研究方向：通信侦察、数据挖掘.

TN929.533

A

1008-4681(2017)02-0038-04