超声无损检测中探头姿态的控制方案

郭科，杨煜普

(上海交通大学,上海 200240)

超声无损检测中探头姿态的控制方案

郭科，杨煜普

(上海交通大学,上海 200240)

针对航空航天领域的复杂曲面的复合材料的检测需求，设计一套5轴联动的检测装置，根据Denavit-Hartenberg(D-H)方法推导出模型的运动学方程，然后利用Rhino软件获取物体表面各离散点的坐标及法向量信息，最终根据运动学方程的逆解控制检测装置各关节的移动量，实现复杂曲面扫查。

超声检测;D-H 方法;运动学正解与逆解;矩阵变换; Rhino

0 引 言

在现代工业领域中，各种金属和非金属结构的构件广泛应用于汽车、风能、航空航天等领域中，假设这些构件自身存在缺陷，轻则导致系统无法正常运行，重则导致严重事故，造成不可挽回的人员伤害和经济损失。无损探伤技术作为检测产品质量的重要手段,保证了材料、零件的可靠性对提高生产效率、降低生产成本起到重要作用，因此越来越受到人们的重视。超声检测由于其检测的快速性、安全性及被测对象范围广等特点，成为应用最广泛的一种无损检测技术[1]。但为了符合现代生产的高效需求，仅仅具备超声子系统是不够的，自动化控制系统在整个检测系统中也是不可或缺的一部分，设备的操控性和检测结果的准确性、可靠性都依赖于自动化控制系统。

1 问题描述

在超声检测中，要求超声波的声束方向要与被检测物体的法线方向保持一致，使得声束垂直入射，缺陷回波和底面回波能沿原路径返回，这样才能保证实现一种高精度，高可靠性的检测。如见图1所示声束入射角与界面波信号衰减关系。横坐标为入射角度,纵坐标为界面波幅值。

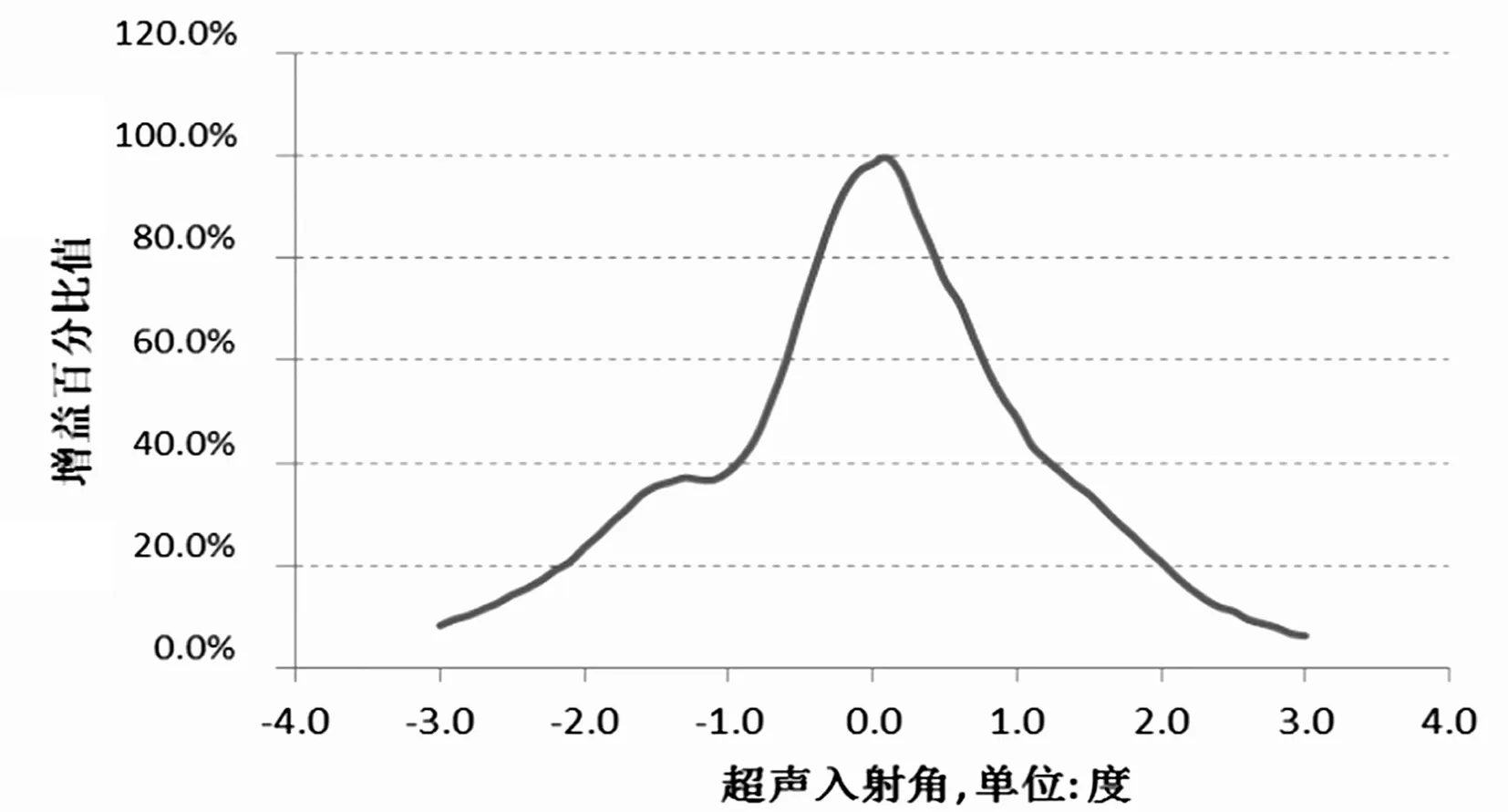
图1 声束入射角与界面波衰减关系

在超声检测的传统领域，大量的板材，棒材和盘环件需要检测，对于这种形状十分规则的材料，扫查轨迹也相对简单，如图2所示。其中X轴为扫查轴，Y轴为步进轴。

图2 规则形状物体的扫查轨迹

对于这种应用，只需在扫查之前，根据超声的回波信号调整好探头的姿态，在扫查过程中超声探头是不需要动态调整的。但近年来航空、航天领域的发展势头迅猛，需要检测一些复杂曲面的复合材料，这就要求在扫查过程中，探头姿态根据被测物体的曲面进行型面追踪检测。如图3所示。

图3 复杂型面的被检测构件

通常的工程解决方案是将被检测物体分成若干区域,各区域的检测区域没有曲率变化,这种检测方式的缺点是效率低下,适应性差,对曲率变化较大的区域无法检测。浙江大学江键等人针对大型复杂曲面工件，提出一种基于模板的扫查方法[2]。该方法首先对第一个工件表面进行采样，重构生成曲面模型，再通过仿型测量修正曲面建模，生成高精度CAD模板。下一个扫描工件在合理获取少量测量点后，根据模板曲面的几何性质进行精确重定位。重建CAD模型后，根据扫查间隔将CAD模型离散化，最后通过逆向求解运动学方程，将曲面上的点坐标转化为检测机械手各关节的运动坐标。这种方式一定程度上确实解决了复杂型面的检测问题，但建立模板时特征点的选取，效率低，并且需要多次优化才能得到精确的模型，对设备使用方的提出较高要求，无法满足现代化生产需求。绝大多数情况下，客户是拥有被检测物体的3D模型的，本文提出一种基于Rhino软件，研究快速获取被检测物体表面法向量的算法，并根据检测机器手的逆运动学方程，得到探头的姿态控制方程，最终实现复杂型面的快速扫描，提高生产效率。

2 基本知识

我们知道空间中的一个点只有3个自由度,即在参考坐标系中沿X、Y、Z三个直角坐标系方向的移动自由度，但在空间中的刚体却有6个自由度,除了上述3个自由度，还有分别绕X/Y/Z轴旋转的自由度。因此，要正确的描述空间中刚体的位置信息,就需要知道物体坐标系原点在参考坐标系中的位置,以及物体坐标系关于这3个参考坐标系的姿态,共6条独立的信息来描述。所以我们用公式1的矩阵来表示刚体在空间中的位置信息[3]30。

(1)

其中前3行*3列为刚体的姿态信息，最后一列为刚体的位置信息。

3 系统实现

3.1 检测机械手模型及其D-H参数表

为了检测曲面模型,我们设计一个具有5个自由度的机械装置,示意图如图4所示,在进行D-H建立各个关节的坐标系时,我们作出如下规定:

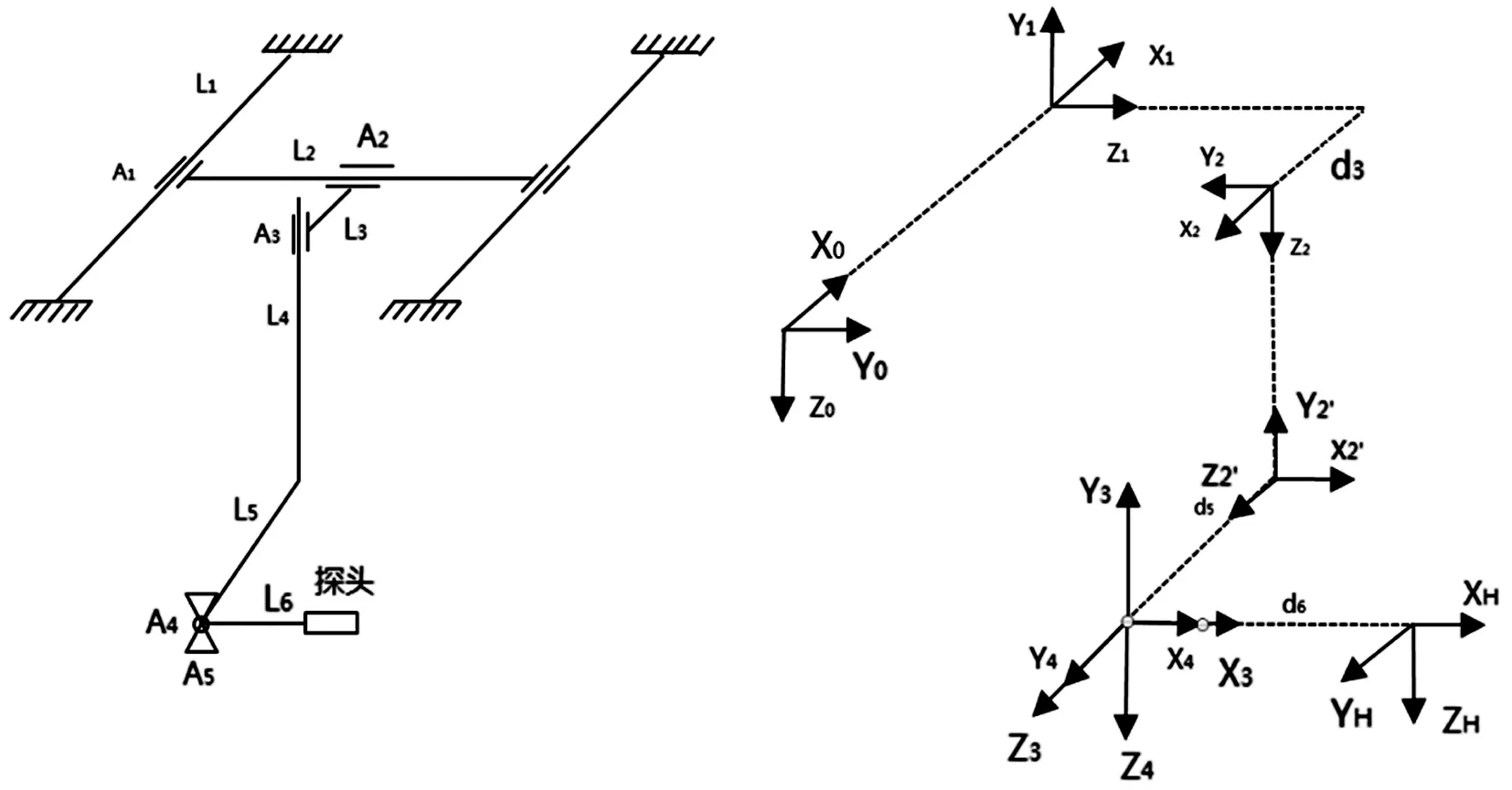
图4 检测装置示意图及各关节坐标系

1)如果为直线运动关节,Z轴为沿直线运动的方向;如果是旋转关节,Z轴为根据右手旋转规则拇指指向的方向。

2)当前关节的X轴为当前关节与前一关节Z轴之间公垂线方向。如果两关节Z轴平行，公垂线有无数条，取与前一关节公垂线共线的一条。如果两关节Z轴相交，没有公垂线，可将垂直于两条Z轴构成的平面的直线作为X轴。

根据以上规则得到系统的D-H参数表如表1所示。

表1 系统的D-H参数表

相邻坐标系转换的变换矩阵见公式2[3]57

(2)

根据公式2 建立检测机械模型的运动学方程:

(3)

3.2 运动学方程的正解和逆解

运动学方程正解就是根据检测机械各关节的移动变量，得到探头终端的位置和姿态；而运动学逆解就是根据探头终端的位置和姿态，得到检测机械各关节的变量值。

根据式3，可得到此检测机械的运动学方程正解为：

(4)

同样根据式3，可得到此检测机械的运动学方程逆解：

(5)

在此项目中，我们需要根据被测材料的形面特征来调整各个关节的变化量，显然我们更关心的是运动学方程的逆解。

3.3 基于Rhino软件获取探头终端的位置和姿态

3.3.1 Rhino 软件介绍

Rhino是美国Robert McNell & Associates公司开发的专业三维造型软件，广泛应用于工业制造、科学研究以及机械设计等领域。Rhino建立的所有物体都是由平滑的NURBS曲线或曲面组成[4]。Rhino自带参数化编辑脚本程序，通过参数的调整直接改变模型形态，或能轻松提取这些形态的精确信息。本论文中就要借助于Rhino强大功能获取物体表面的各离散点的空间坐标及法向量信息。

3.3.2 在Rhino中获取曲面离散点的位置和法向量

由于Rhino软件建立的曲面模型都是NURBS曲面,NURBS表面含有矩形的UV曲线网格,当对一个曲面S进行操作时,一般也将它划分为UV单元格,每一个(U,V)坐标都对应于三维欧式空间中一点(X,Y,Z)。在RhinoScript中编写如下脚本获取曲面离散点的空间坐标及其法向量：

CallMain()

SubMain()

arrOrigin=Rhino.GetPoint("Plane origin")

If IsArray(arrOrigin) Then

arrPlane = Rhino.ViewCPlane

If IsArray(arrPlane) Then

Rhino.ViewCPlane Rhino.CurrentView, Rhino.MovePlane(arrPlane, arrOrigin)

End if

End if

Strsurface=rhino.GetObject("Please select Surface", 4 + 8)

If IsNull(strsurface) Then Exit Sub

secu = 100

secv = 100

Udomain = rhino.SurfaceDomain(strsurface, 0)

Vdomain = rhino.SurfaceDomain(strsurface, 1)

Rhino.Print "Domain in U direction: " & CStr(Udomain(0)) & " to " & CStr(Udomain(1))

Rhino.Print "Domain in V direction: " & CStr(Vdomain(0)) & " to " & CStr(Vdomain(1))

For i=0 To secu

For j=0 To secv

Uparam=Udomain(0)+i* ((Udomain(1) - Udomain(0)) / secu)

Vparam=vdomain(0)+j * ((Vdomain(1) - Vdomain(0)) / secv)

arrpoints=rhino.EvaluateSurface(strsurface, array(uparam, vparam))

arrnormals=rhino.SurfaceNormal(strsurface, array(uparam, vparam))

Collec(i, j) = arrpoints

Normal(i, j) = arrnormals

Rhino.Print rhino.Pt2Str(Collec(i, j))

Rhino.Print rhino.Pt2Str(Normal(i, j))

Next

Next

End Sub

其中3～9行指定检测物体坐标系的原点;10～11行指定

检测物体的检测面;15～18行返回检测面在指定U V方向上的域;19～31行根据参数secu和secv将整个平面离散化并返回各个点的空间坐标及其法向量。注意在第10步指定检测面的时候一定要选取检测面的反面，这样才能保证得到的法向量跟探头方向一致。法向量仅仅是对应姿态矩阵(公式(1))中nx,oy,az三个分量信息，但姿态矩阵是有下列约束条件的:

(1)个向量n、o和a向量相互垂直。

(2)每个由方向余弦表示的单位向量的长度必须为1。

由这些约束条件可转化为6个约束方程，就可以解出完整的姿态矩阵。

以上步骤得到在指定的物体坐标系中的各个点的坐标和姿态，还需要转化为检测坐标系中坐标和姿态，才能根据逆运动学方程-式(5)得到检测机械各关节的运动位置,所以要求出检测坐标系与物体坐标系之间的变化矩阵M。

对于两个坐标系之间的变化矩阵，我们在这里不做详细推导，直接给出转化关系如下:

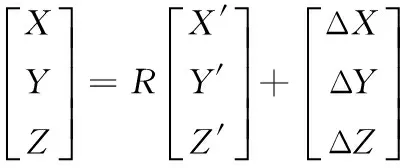
(6)

r11=cosβcosγ,r12=cosβsinγ,r13=-sinβ,
r21=sinαsinβcosγ-cosαsinγ,r22=sinαsinβsinγ-cosαcosγ,
r23=sinαcosβ,
r31=cosαsinβcosγ+sinαsinγ,
r32=cosαsinβsinγ-sinαcosγ,
r33=cosαcosβ

其中α,β,γ为绕X,Y,Z轴的旋转角.

需要得到变化矩阵，即求解α,β,γ,ΔX,ΔY,ΔZ6个未知量[5]。

为了求坐标系间的转化参数,通常使用检测机械利用超声的测距原理选取被测工件的3个特征点Pi(i=0,1,2),然后在Rhino 3D模型曲面上取3个位置完全对应的点,Qj(j=0,1,2),使用文献6中的基于罗德里格矩阵的转换方法,就可以得到两个坐标系之间的旋转矩阵R, 平移矩阵可以根据公式T=P0-RQ0得到[6]。

4 结束语

本文针对复杂曲面的复合材料的检测,设计一套5轴联动的检测装置模型，并推导出此检测模型的正逆运动学方程，提出使用Rhino软件获取检测面的空间坐标及法向量的新方法，极大地简化建模的过程，提高生产效率。

[1] 张旭辉，马宏伟.超声无损检测技术的现状和发展趋势[J].无损检测，2002,40(455):24-26.

[2] 江健.航空构件一体化超声成像检测的若干关键技术研究.[D].浙江:浙江大学,2005.

[3] SAEED B NIKU.机器人学导论[M].孙富春，译. 北京:电子工业出版社,2013.

[4] 王文栋.Rhino Script参数建模[M]. 北京:中国青年出版社,2011.

[5] 胡宏伟，李雄兵，倪陪君,等 复杂型面工件超声自动检测中的匹配定位方法[J].中国机械工程，2012,23(2) :195-198.

[6] 张卡,张道俊,盛业华,等 三维坐标转换的两种方法及其比较研究[J].数学的实践与认识,2008,38(23):121-128.

The Control Scheme for Probe Posture in Ultrasonic Nondestructive Testing

Guo Ke, Yang Yupu

(Shanghai Jiao Tong University, Shanghai 200240, China)

To meet the requirement for testing composite materials with complex surfaces in the aerospace field, this paper designs a 5-axis testing device. The kinematical equation of the model is deduced in the Denavit-Hartenberg (D-H) method. Then, the coordinates and normal vector information of discrete points on the surface of the object are obtained by use of Rhino software. Finally, amounts of movement of the joints of the inspection device are controlled through inverse solution of kinematical equation to realize scanning of complex surfaces.

ultrasonic testing； D-H method； forward kinematics and inverse kinematics；matrix transformations；Rhino

10.3969/j.issn.1000-3886.2017.01.025

TP273.5

A

1000-3886(2017)01-0084-04

郭科(1981-),男,江苏溧阳人,硕士生,主要从事工业自动化研究。 杨煜普(1957-),男, 河南洛阳人,教授, 研究方向:经网络、智能控制。

定稿日期: 2016-07-21