基于非线性微分跟踪器的无差拍控制在APF中的应用
2017-05-13龙英文孙玉鸿王敬华
龙英文,孙玉鸿,王敬华
(1.上海工程技术大学,上海 201620; 2.上海追日电气有限公司,上海 200331)
基于非线性微分跟踪器的无差拍控制在APF中的应用
龙英文1,孙玉鸿2,王敬华1
(1.上海工程技术大学,上海 201620; 2.上海追日电气有限公司,上海 200331)
文中将无差拍控制和非线性微分跟踪器相结合,利用两者的优势, 提出一种基于APF无差拍控制器中引入非线性微分跟踪器,用以补偿负载电流变化扰动APF控制器的影响,从而避免过于复杂的谐波电流提取算法。该算法与传统的APF谐波提取算法不同,可以有效地降低电网电流的THD。仿真和实验结果都证明了所提控制算法方法的可行性。
无差拍控制;跟踪微分器;有源电力滤波器;谐波电流,有源电力滤波器
0 引 言
随着电力电子技术的飞速发展,各种电力电子装置得到了广泛的使用,也给电力系统带来了严重的谐波污染。有源电力滤波器(Active Power Filter, 简称APF)作为一种实时补偿电网谐波的装置得到了广泛的研究和应用。实时、准确地检测电网谐波电流以及快速、高精度地追踪谐波电流参考是APF有效补偿谐波电流的关键[1-2]。跟踪参考信号的控制方法决定着APF补偿性能的优劣,典型的谐波电流跟踪方法包括滞环电流控制、无差拍控制、单周期控制和重复控制方法等[3-6]。其中无差拍控制具有动态响应快的特点,但因属于开环控制,存在稳态误差,其电流跟踪效果需要有合适的电流预测方案来保证,并且无差拍控制对系统参数依赖性较强,控制精度会随着系统参数的变化而变化。但是随着数字信号处理器性能的不断提高,使得一些复杂控制算法的实现成为可能,无差拍控制技术在APF中将会得到进一步的应用,例如文献[7]提出基于内置重复控制原理,利用重复控制器修正无差拍控制中周期性的控制偏差,改善无差拍控制的缺陷,消除周期性稳态误差;文献[8]基于外推多项式法预测谐波电流参考,预测的准确度取决于所取阶次,选取的阶次越高,预测得越准确,同时计算量越大。
设计APF控制器时,如果能够获得负载电流的有效估计,那么就可以对原有控制器进行补偿,从而获得更好的控制效果。非线性跟踪微分器[9-11]利用二阶最速开关系统跟踪输入信号,具有无超调无抖震的特点,克服了传统滑模控制中存在的抖震现象[12]。利用非线性跟踪微分器获得对负载电流信号变化的估计,并在无差拍控制律中对其进行补偿。文中通过在APF无差拍控制器中引入非线性跟踪微分器,用以补偿负载电流变化扰动,从而避免采用计算过于复杂的谐波量估计等补偿方法。
1 无差拍电流跟踪控制
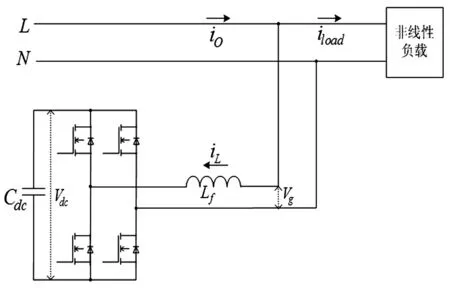
图1 全桥逆变电路
如图1所示,以单相全桥单BUS架构,双极调制方式APF为例,假定电网带恒流负载(diO/dt=diL/dt)。则APF系统状态方程如下:
(1)
其中iL为APF滤波电感电流,iO为电网输出电流,iload为负载电流。根据上式,可以得到APF电流环无差拍控制器:

(2)
假定电网输出电流iO完美跟踪市电波形,即iO=kVg,将上述占空比代入电压环方程可得:
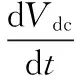
(3)

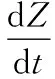
(4)
设定Vg=Vmsinωt,结合公式(3)和(4)可以得到:
(5)
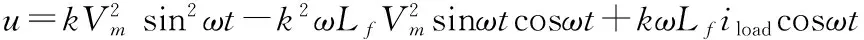
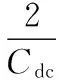
(6)
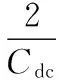
(7)
上式平衡条件可重新写作如下形式

(8)
2 无差拍电流跟踪控制的改进
在前述APF电流环无差拍控制器设计中,假设系统具有恒流负载,则离散化后得到的无差拍控制器如下:

(9)
其中Ts为系统采样周期。如果利用非线性无差拍控制器可以获得负载电流iload的有效预测,则修正后的无差拍控制器可写作:
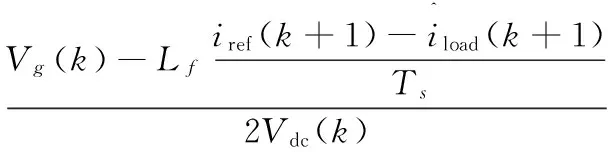
(10)
但在实际控制系统中,我们获得的采样信号是电网输出电流iO,而并不会测量负载电流信号,因此我们无法直接获得非线性微分跟踪器中需要的输入信号Uin。对此,我们做如下的一个转换处理。
对无差拍控制器而言,如果负载电流具有恒流性质,则理论上该控制器能够使得电网输出电流iO(k+1)完美跟踪参考电流信号iref(k+1)。那么实际系统中,由于负载电流变化造成的跟踪误差δ=iref(k+1)-iO(k+1),可表述为非线性微分跟踪器中误差信号σ=z1-Uin的函数δ=g(σ),且该函数满足单调性和保号性。因此,我们可以设计非线性微分跟踪器如下:
(11)
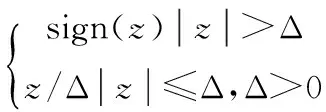
同样可以获得负载电流微分量的有效跟踪。由此,设计补偿后的无差拍控制器如下:

(12)
3 仿真
文中采用MATLAB Simulink 模块下的S-Function进行C语言全数字控制仿真, 其中,Vg=311sin100πt,采样周期Ts=50*10-6s,Lf=850 μH,母线电容Cdc=1 500 μF,全桥电路采用双极性调制方式。
图2和图3为非线性RCD负载(10 000 μF/10 Ω)时分别采用无差拍控制和无差拍+非线性微分跟踪的仿真图,其中曲线1、2、3分别表示为负载电流、负载基波电流和APF补偿后的输入市电电流。图2中市电输出电流的THD为5.3%~5.4%;图3中R=109,Δ=1,市电输出电流的THD为2.2%~2.5%。
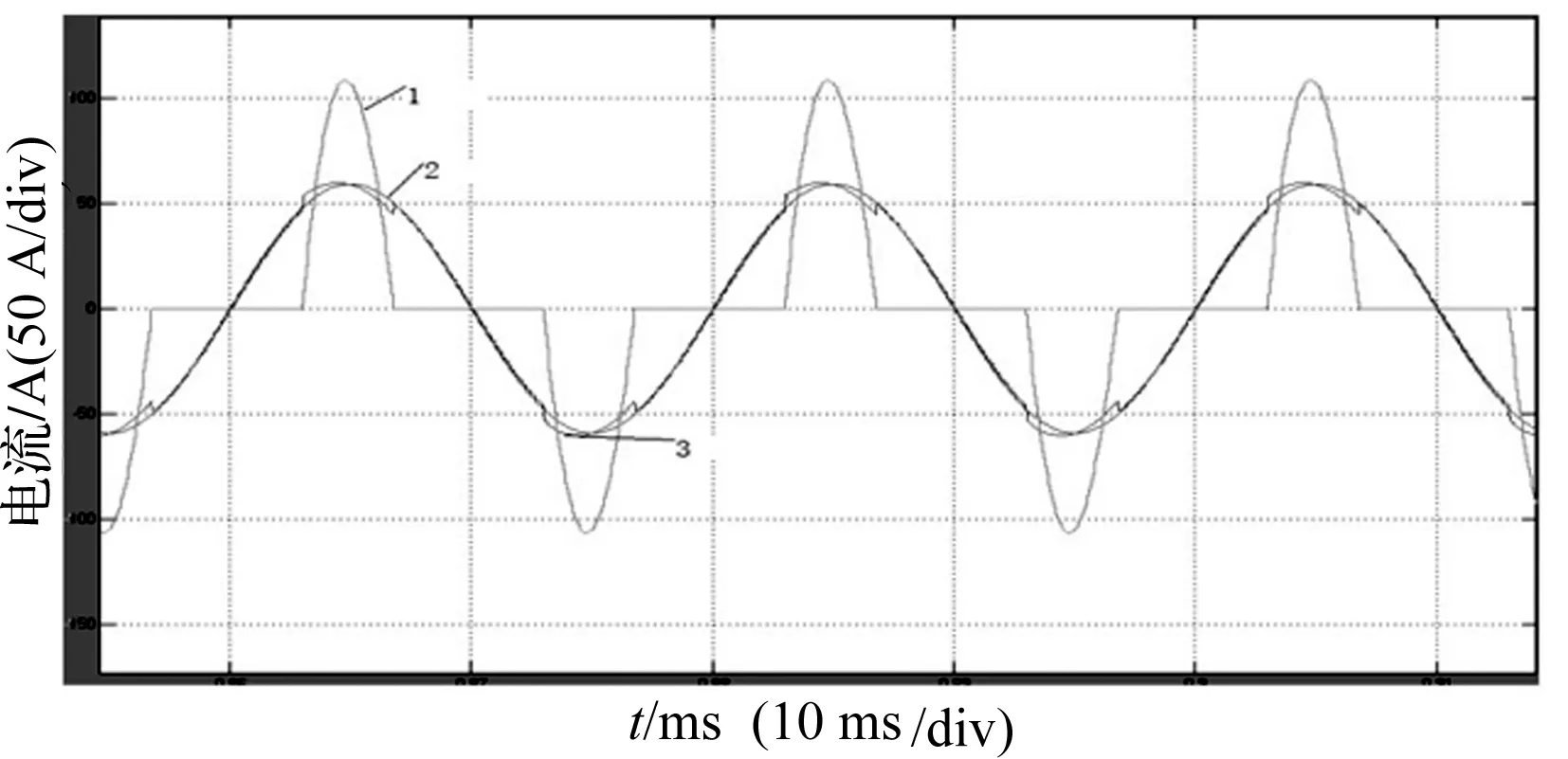
图2 无差拍控制器仿真图
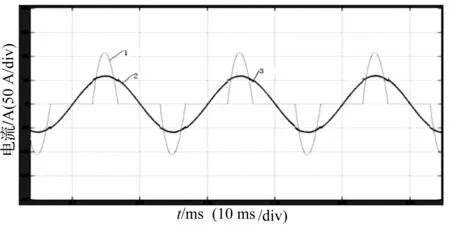
图3 无差拍控制器+非线性微分跟踪器仿真图

图4 无差拍控制器仿真图

图5 无差拍+非线性微分跟踪器仿真图
图4和图5为负载电流包含50安培基波和25安培5次谐波时单相APF分别采用无差拍控制和无差拍+非线性微分跟踪的仿真图。其中曲线1、2、3分别表示为负载电流、负载基波电流和APF补偿后的输入市电电流。图4中市电输出电流的THD为4.1%~4.3%;图5中R=109,Δ=1,市电输出电流的THD为1.9%~2.0%。
图6和图7为非线性RCD负载(10 000 μF/10 Ω)时分别采用无差拍控制和无差拍+非线性微分跟踪的仿真图,图6中市电输出电流的THD为9.4%左右;图7中R=109,Δ=1,市电输出电流的THD为4.6%~5.1%。
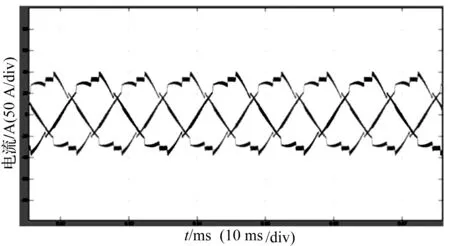
图6 无差拍控制器作用下三相电网输出电流波形

图7 无差拍+非线性微分跟踪器作用下三相电网输出电流波形
对无差拍+非线性微分跟踪器控制律,文中在对单相和三相不同负载下分别作了对比。从仿真结果看,非线性微分跟踪器的加入可以明显改善APF的控制效果,电网输出电流谐波降低50%左右。
4 实验
为了进一步验证仿真结果,本文无差拍改进算法在上海追日电气有限公司单相APF实验平台进行试验,模拟市电电压为176 V,采样周期Ts=50*10-6s,Lf=850 μH,母线电容Cdc=1 500 μF,负载为非线性RCD负载(2 000 μF/10 Ω)。图中通道1为市电输出电流(20 A/格),通道2为市电电压(100 V/格)。
图8为无差拍控制单独控制的输出电流和市电电压波形,输出电流THD为8.9%左右。图9-图11为无差拍+非线性微分跟踪器作用下的输出电流和市电电压波形。图8中R=109,Δ=1,输出电流THD为8.7%左右;图9中R=109,Δ=1,输出电流THD为5.5%左右;图10中R=109,Δ=1,输出电流THD为4.2%左右;图11中R=109,Δ=1,输出电流THD为3.8%左右。

图8 无差拍控制输出电流和市电电压波形

图9 无差拍+非线性微分跟踪器作用下输出电流和市电电压波形

图10 无差拍+非线性微分跟踪器作用下输出电流和市电电压波形

图11 无差拍+非线性微分跟踪器作用下输出电流和市电电压波形
5 结束语
文中将无差拍控制和非线性微分追踪器相结合,利用两者的优势,在基于APF无差拍控制器中引入非线性微分跟踪器,实现对APF谐波补偿控制,用以补偿负载电流变化扰动的影响,而避免计算过于复杂的谐波分量提取算法。该算法与传统的APF谐波提取算法不同,利用非线性微分追踪器能够实现快速追踪的特点,可以有效地降低电网电流的THD。最后的仿真和实验验证了该补偿算法的准确性和可行性。
[1] KETZER M B, JACOBINA C B. Virtual flux sensorless control for shunt active power filters with quasi-resonant compensators [J]. IEEE Transactions on Power Electronics, 2016, 31(7):4818-4830.
[2] TRINH Q N, LEE H H. An advanced current control strategy for three-phase shunt active power filters [J]. IEEE Transaction on Industrial Electronics, 2013, 60(12): 5400-5410.
[3] 肖丽平,童朝南,高润泉.改进的有源电力滤波器滞环电流控制策略[J].电力系统自动化,2014, 38(12):119-124.
[4] 韩伟,王大志,刘宝成.基于复合预测的无差拍谐波电流跟踪控制[J].仪器仪表学报, 2014, 35(6):1425-1432.
[5] 何英杰,刘进军,王兆安,等. 基于重复预测原理的三电平APF无差拍控制方法[J]. 电工技术学报,2010, 25(2):114-120.
[6] 徐群伟, 钟晓剑, 胡健, 等. 基于误差迭代 PI 和改进重复控制的 APF 补偿电流控制[J]. 电力系统自动化, 2015,39(3):24-131.
[7] 周娟,秦静,王子绩,等.内置重复控制器无差拍控制在有源滤波器中的应用[J].电工技术学报,2013, 28(2):233-238.
[8] ODABIC M, BIAGINI V, ZANCHETTA P, et al. One-sample-period-ahead predictive current control for high-performance active shunt power filters [J]. The Institution of Engineering and Technology, 2011, 4(4):414-423.
[9] 韩京清, 王伟. 非线性跟踪-微分器[J]. 系统科学与数学,1994, 14(2):177-183.
[10] 史永利, 侯朝桢. 改进的非线性跟踪微分器设计[J]. 控制与决策, 2008, 23(6):647-650.
[11] 谢云德,李晓龙,佘龙华. 一种基于边界特征的简易非线性二阶离散跟踪微分器的设计[J]. 控制与决策, 2014, 29(6):1120-1124.
[12] 杨龙月,刘建华,王崇林. 有源电力滤波器精确反馈线性化准滑模变结构控制[J]. 中国电机工程学报, 2014, 34(33):5868-5875.
Application of Deadbeat Control Based on Nonlinear Tracking Differentiator in APF
Long Yingwen1, Sun Yuhong2, Wang Jinghua3
(1. Shanghai University of Engineering Science, Shanghai 201620, China;2. Shanghai Surpass Sun Electric Co. Ltd., Shanghai 200331, China)
In this paper, the APF deadbeat controller and nonlinear tracking differentiator are combined, and their advantages are used to compensate for disturbance of the APF controller by variation of the load current, thus avoiding over complicated algorithm of harmonic current extraction. Different from the traditional APF harmonic extraction algorithm, this algorithm can effectively reduce grid current THD. Simulation and experimental results prove the feasibility of the presented control algorithm.
deadbeat control; tracking differentiator; active power filter (APF) ; harmonic current
10.3969/j.issn.1000-3886.2017.01.004
TM712
A
1000-3886(2017)01-0010-03
龙英文(1974-),山东荣成人,博士,讲师,电力电子控制技术研究。
定稿日期: 2016-07-25
