结合矢量和直接功率控制的双馈风电机组研究
2017-05-13赵一心
赵一心
(吉林工程职业学院,四平136001)
0 引 言
随着工业发展,电力需求不断增加,而传统能源的过量使用导致了严重的环境问题和能源危机,因此,新能源得到了广泛研究和发展,尤其是风能占能源利用比重越来越高,预测到2020年将达到世界范围总发电量构成的10%,并有可能进一步发展到现有占比的一倍以上[1-2]。
风力发电机组作为风电场的核心设备,可以分为固定转速和变转速2种类型[3-4]。而变转速的风电机组由于具有最大风能捕获,较低的机械应力和噪声,较高电能质量等优点得到了广泛商业应用[5-6]。变转速风电机组可以进一步细分为基于永磁同步发电机(以下简称PMSG)和全功率变流器的类型和基于双馈感应电机(以下简称DFIG)和半功率变流器的类型[7-8]。DFIG尤其适合大功率场合,如兆瓦级风电,因为其变流器成本较低,损耗较小。从控制的角度,DFIG分为转子侧RSC和电网侧GSC控制,RSC控制定子有功和无功功率,GSC控制直流电压,也输出独立的无功功率到电网[9-10]。矢量控制(以下简称VC)是DFIG型风电机组常用的控制方案,其优点在于较好的稳态性能,较小的功率波动,较低的变流器开关频率等[11-13]。但是该方法对电机参数变化较为敏感,鲁棒性不好,且实时计算量较大。同时,算法中使用的PI控制器必须调整好参数以满足全工况下系统稳定,这将折衷动态响应速度[14]。因此,为了克服VC的缺点,一种非线性控制方法,即直接功率控制(以下简称DPC)被提出来[15-17]。它的优点在于暂态响应较快,对电机参数的鲁棒性较好和实时计算量小。但是其存在显著的功率抖震,这是由于滞环控制器的高带宽导致的,同时存在输出电流谐波较大的问题,电机起动和低速工况下的性能也不好[18-19]。
考虑到上述问题,文献[20-21]在永磁电机驱动领域提出了结合矢量和直接功率控制(以下简称CVDPC)的方法,而文献[22-23]在感应电机驱动领域也提出了CVDPC方法。但是CVDPC在双馈风电机组上的应用鲜有研究,因此,本文在前述研究的基础上,集中对VC和DPC进行了比较,总结了这两种方法之间的数学联系,从而提出了一种新型的CVDPC的双馈风电机组控制策略,设计的控制器作用于机组的RSC侧,最后通过搭建的仿真模型系统,对控制策略进行了仿真验证。
1 矢量控制和直接功率控制
1.1 矢量控制
在双馈风电机组控制策略中,VC方案是较为常见的。在VC方法中,可以通过控制转子的电流矢量来实现对定子有功和无功功率的解耦控制。定子有功和无功功率输出参考分别由最大功率点跟踪算法MPPT(Maximum Power Point Tracking)和电网需求决定。控制器通常使用定子磁场定向SFOF(Stator Flux-Oriented Frame),但这使得VC的性能很大程度上依赖对定子磁链位置的精确观测,从而较容易受到电压畸变或电机参数扰动的影响。因此下述将使用定子电压定向SVOF(Stator Voltage Oriented Frame),同时为了从定子电压中提取出同步信号,使用了锁相环PLL(Phase Locked Loop)技术,从而定子有功功率Ps和无功功率Qs表达式如下[12]:
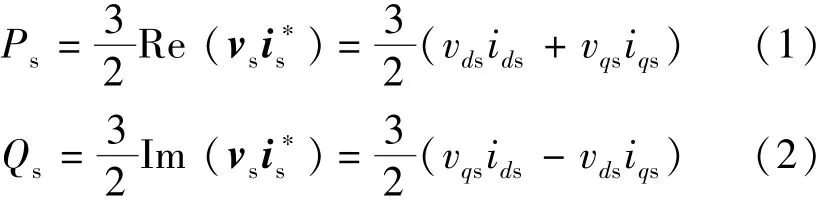
式中:vs为定子的输出电压矢量;i*s为定子电流参考矢量;vds,ids和vqs,iqs分别为d轴和q轴的电压电流分量。当使用定子电压定向后,上式可以简化:

此时电流ids和iqs的表达式:

式中:Ls和Lm为定子绕组电感和互感;idr和idr分别为转子d,q轴电流;ωs为定子角速度。将式(5)和式(6)代入式(3)和式(4),可得:


因此,定子有功和无功功率可以通过转子电流idr和iqr控制,具体的双馈风电机组的机侧矢量控制框图如图1所示。

图1 机侧VC框图
图1 中,vdc为直流侧电压;和为有功和无功功率参考;和为转子电流参考;和为转子电压参考;σLr为转子漏感;和v*
c为定子三相电压参考;θr,θs和θm分别为转子角、定子角和滑差角;iar,ibr和icr为机侧输出三相电流;vas,vbs和vcs为定子三相电压;p为微分算子。
1.2 直接功率控制
在DPC方法中,将不再使用电流控制环,而是直接对定子有功和无功功率进行控制。具体的DPC方法可以用以下方程进行表述[16]:
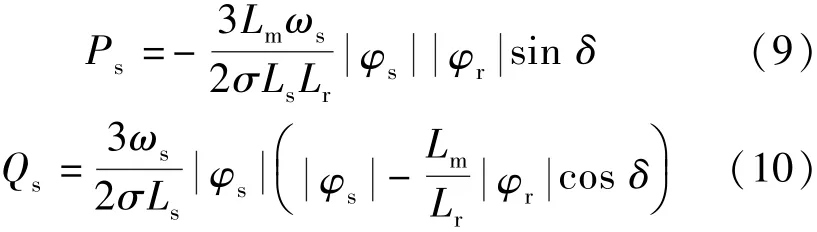
式中:Lr为转子电感;σLs为定子漏感;φr为转子磁链;φs为定子磁链;δ为转子磁链和定子磁链之间的相角差。假定定子和转子磁链近似为常数,对式(9)求微分可以得到:
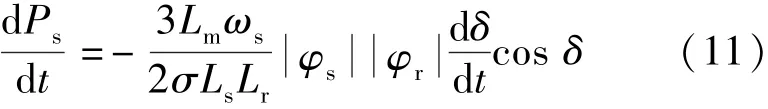
式(11)说明定子有功功率动态决定于δ,因此可以通过改变δ实现对有功功率的快速控制。假定定子磁链和δ近似为常数,对式(10)求微分可以得到:

式(12)说明定子无功功率动态取决于转子磁链幅值的变化,因此可以通过改变转子磁链实现对无功功率的快速控制。而改变转子磁链可以通过将合适的变流器电压矢量作用在转子绕组上实现。转子电压微分方程在很短时间Δt内能近似表示如下:

式中:Rr为转子电阻;vr为转子电压。在知道转子磁链φr位于哪个扇区后,6个变流器电压矢量就能合适的作用来控制φr的位置和幅值。因此,DPC的框图如图2所示。图2中定子有功和无功功率与参考值比较后的差值输出给滞环控制器,然后滞环控制器输出uPs和uQs给开关动作表,后者结合扇区位置信息选择合适的电压矢量给PWM生成器生成功率器件的控制脉冲。具体开关动作表如表1所示[15]。

图2 机侧DPC框图

表1 DPC时的转子电压矢量开关动作表
1.3 矢量控制和直接功率控制之间的数学联系
以下将分析矢量控制和直接功率控制在数学上的联系。在VC方法中,若定子电压为常数,那么从式(7)和式(8)中可得到:

另一方面,图3为DPC在一个开关周期内磁链矢量变化的规律。从图3中可以看出,在一个开关周期内,转子磁链矢量从φr变化到φr1,而由于定子时间常数远大于开关周期,定子磁链矢量φs基本保持不变,而转子磁链的变化量Δφr可以分解为径向分量ΔφF和切向分量ΔφT,前者影响到磁链幅值,而后者关系到磁链相角位置。

图3 DPC中一个开关周期的磁链矢量变化
因此,根据图3,以及式(9)和式(10),定子有功和无功功率的变化可写为:

考虑到Δδ很小,故 cos(Δδ)近似等于1,从而有:

将式(9)和式(10)代入式(15)和式(16)可以得到:

在式(19)中,右侧括号中的第2项是由受限的变流器电压矢量,以及没有区分径向和切向磁链分量造成的,通过降低滞环控制器的带宽能显著减小该项的幅值;对于右侧括号中的第3项,含有2个小量的乘积,属于微小量,因此也可以忽略。从而得到:

因此根据式(20)、式(21),可得到线性关系如下:

式(22)说明,定子输出有功和无功功率增量分别是与负的转子磁链径向分量和轴向分量的增量成线性比例关系的。对比式(14)和式(22),可以得到如下结果:

式(23)意味着DPC中转子磁链径向分量和轴向分量的增量与VC中d轴和q轴转子电流的增量成线性比例关系。因此,DPC和VC存在明显的内在数学联系。该结论为下面新型控制方案设计提供了理论依据。
2 结合矢量和直接功率控制的新型控制方法
2.1 基本思路
如前所述,DPC中的定子有功功率的滞环控制和VC中转子d轴电流控制存在着本质上的共通处。另一方面,DPC中的定子无功功率的滞环控制和VC中转子q轴电流控制也是有数学联系的。基于此,可以考虑一种新型控制策略将DPC和VC结合起来,这种新的控制方法可能同时获取两种传统控制策略的优势。
前述已经说明,DPC由于能够快速地选择功率器件开关矢量状态,因此具有较快的动态响应,所以考虑对这部分进行保留,然后将VC中电流dq解耦控制融入,取代DPC中的直接功率滞环,从而得到了新型控制器的设计思路。
2.2 新型控制器设计
图4为新型的双馈风电机组的CVDPC控制器。从图4中可以看出,其分为矢量电流控制环部分和直接功率控制部分,控制系统中首先是由功率计算模块得到实时的有功和无功功率信息,然后和参考值比较,结果输出到传统的d轴和q轴PI电流环运算,这和VC一样,具体涉及到旋转坐标系变换等,然后经由滞环电流控制器,计算后输出给开关动作表,开关动作表还有一个扇区信息输入来自于扇区判断模块,其基于定子和转子电流,以及转子位置对转子磁链所在扇区进行定位。最后开关动作表输出合适的电压矢量给PWM生成模块进行功率器件控制脉冲的生成,从而完成整个控制过程。
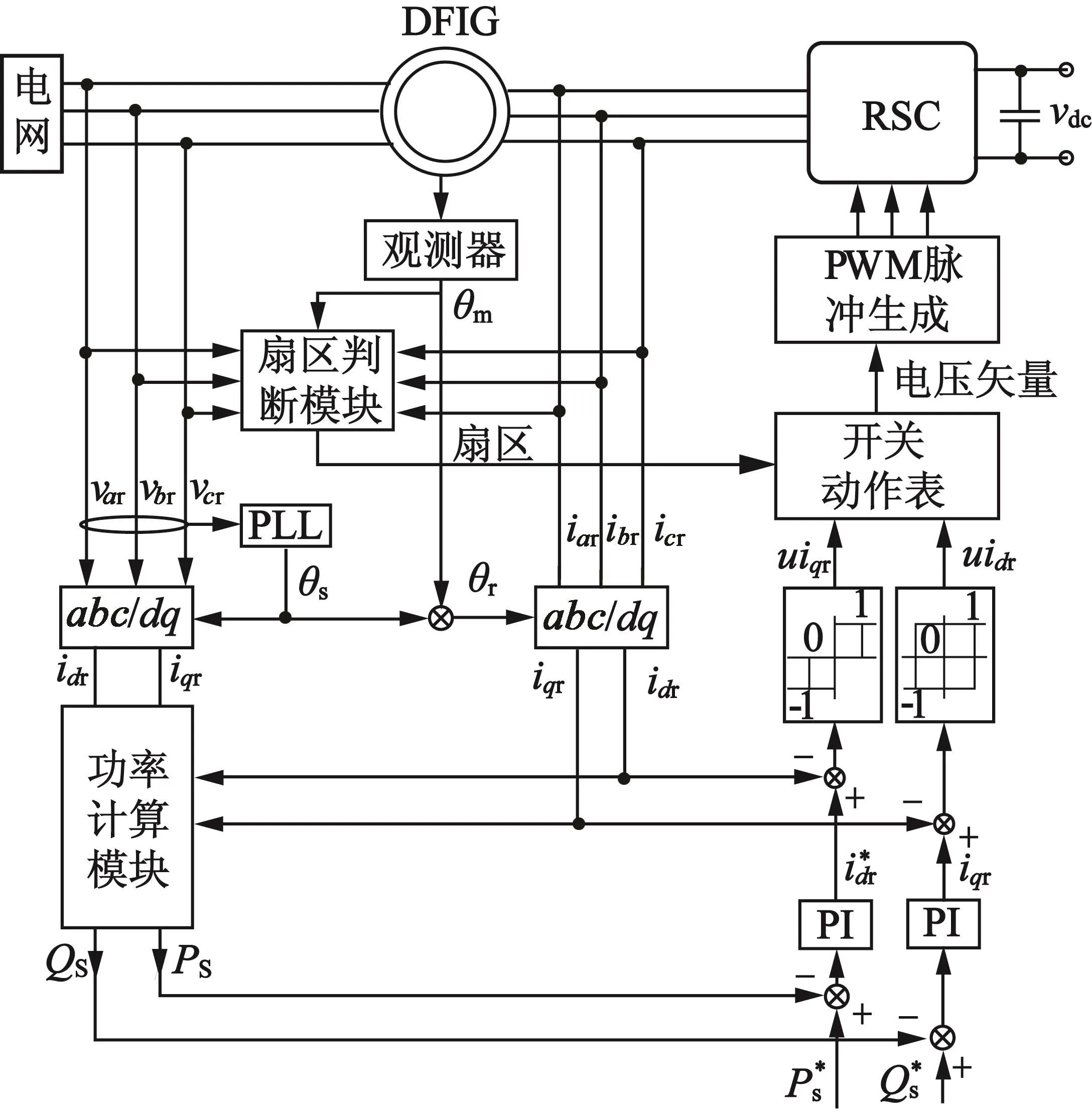
图4 结合VC和DPC的控制器框图
3 仿真验证
为了检验前述所介绍的结合矢量和直接功率控制的双馈风电机组控制策略的有效性,基于MATLAB/Simulink仿真平台搭建了风电场仿真模型,并进行了仿真研究。图5为仿真系统模型,其中风电场由6组1.5 MW的DFIG构成,容量为10 MVA,具体的仿真系统参数如表2所示。

图5 仿真系统示意图

表2 仿真系统相关参数
基于仿真模型,进行了系统稳态和动态性能仿真。仿真模型中电流滞环控制的带宽设置为δ=2Δδ=6.28,从而获取了一个转子电流跟踪精度和RSC侧最大开关频率的平衡。对于PI控制器参数的优化设置,需要同时在3种控制方法之间取得一个平衡。因此,引入了PI参数优化引入了标准型的最优遗传算法(以下简称GA),其中定子有功和无功功率控制环和转子电流环优化时设定转子转速恒定ωr=1.2ωs,定子无功功率恒定Qrs=0。优化算法中定义目标函数:

GA算法中每一步优化,即目标函数的收敛过程如图6所示。
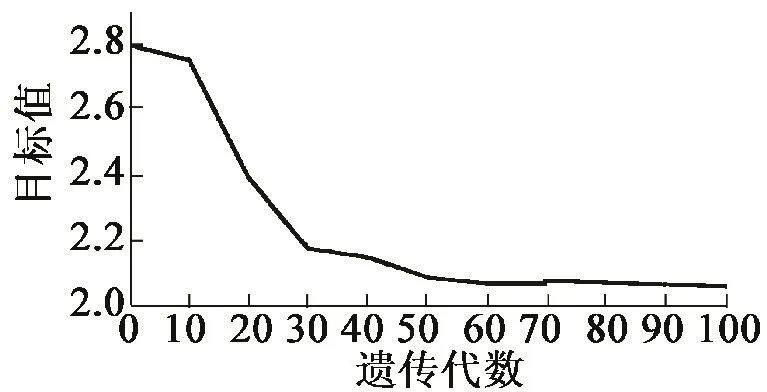
图6 GA算法中目标函数的收敛过程
如图7至图11为系统稳态仿真结果。仿真中设置风速固定为15 m/s,基于最优功率速度曲线,发电机转速ωr=1.2ωs,此时6组发电机通过定子传送有功功率Ps为7.58 MW,转子传送有功功率Pr为1.42 MW,为了实现机侧最大电流使用率,定子绕组不输出无功功率。从图中可以看出,CVDPC的功率波动程度和VC接近,只有约0.55%,而DPC下的功率波动明显较大,接近2.22%。

图7 发电机转速稳态仿真结果

图8 总有功功率稳态仿真结果
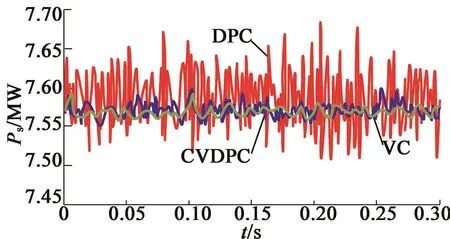
图9 定子总有功功率稳态仿真结果
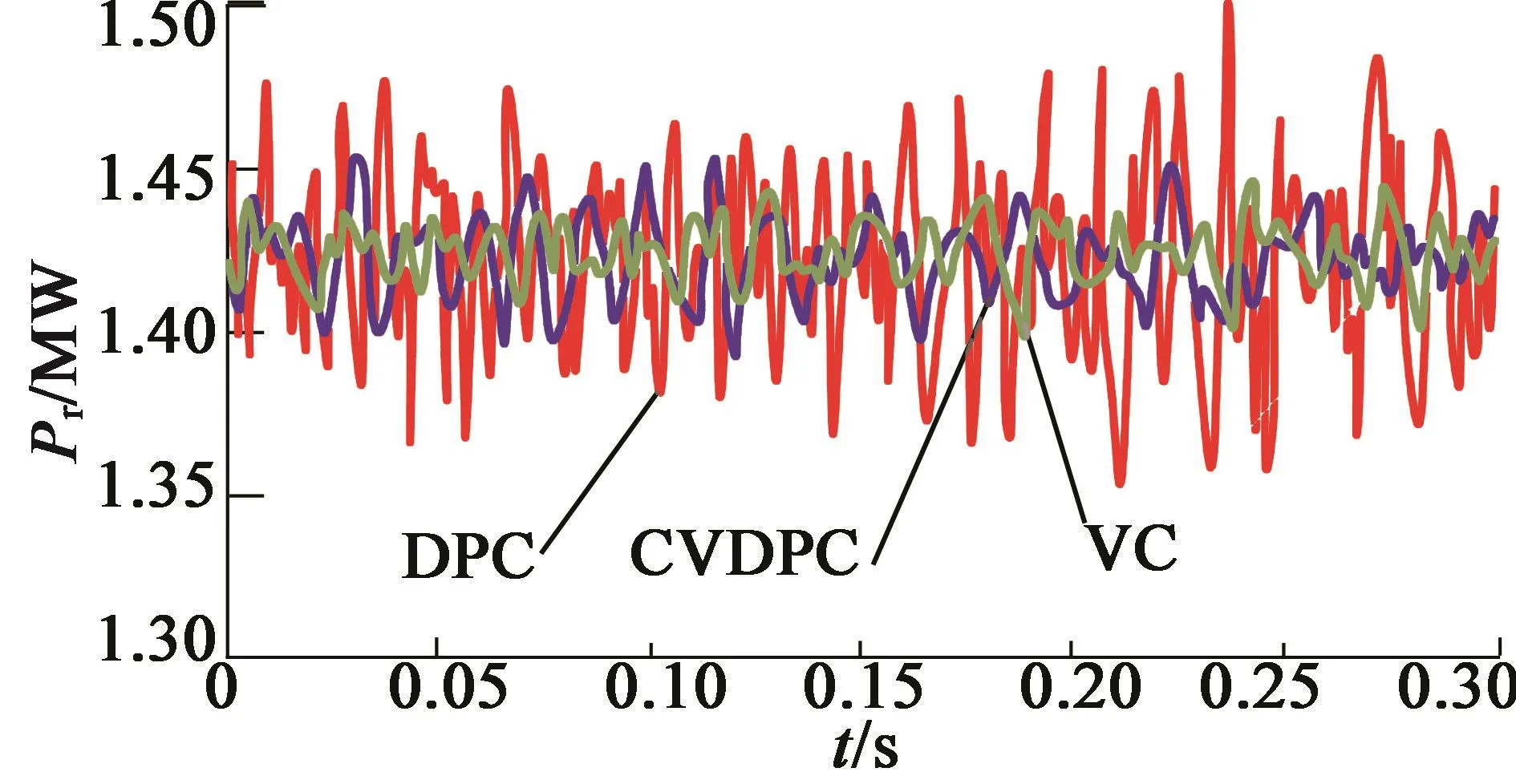
图10 转子总有功功率稳态仿真结果
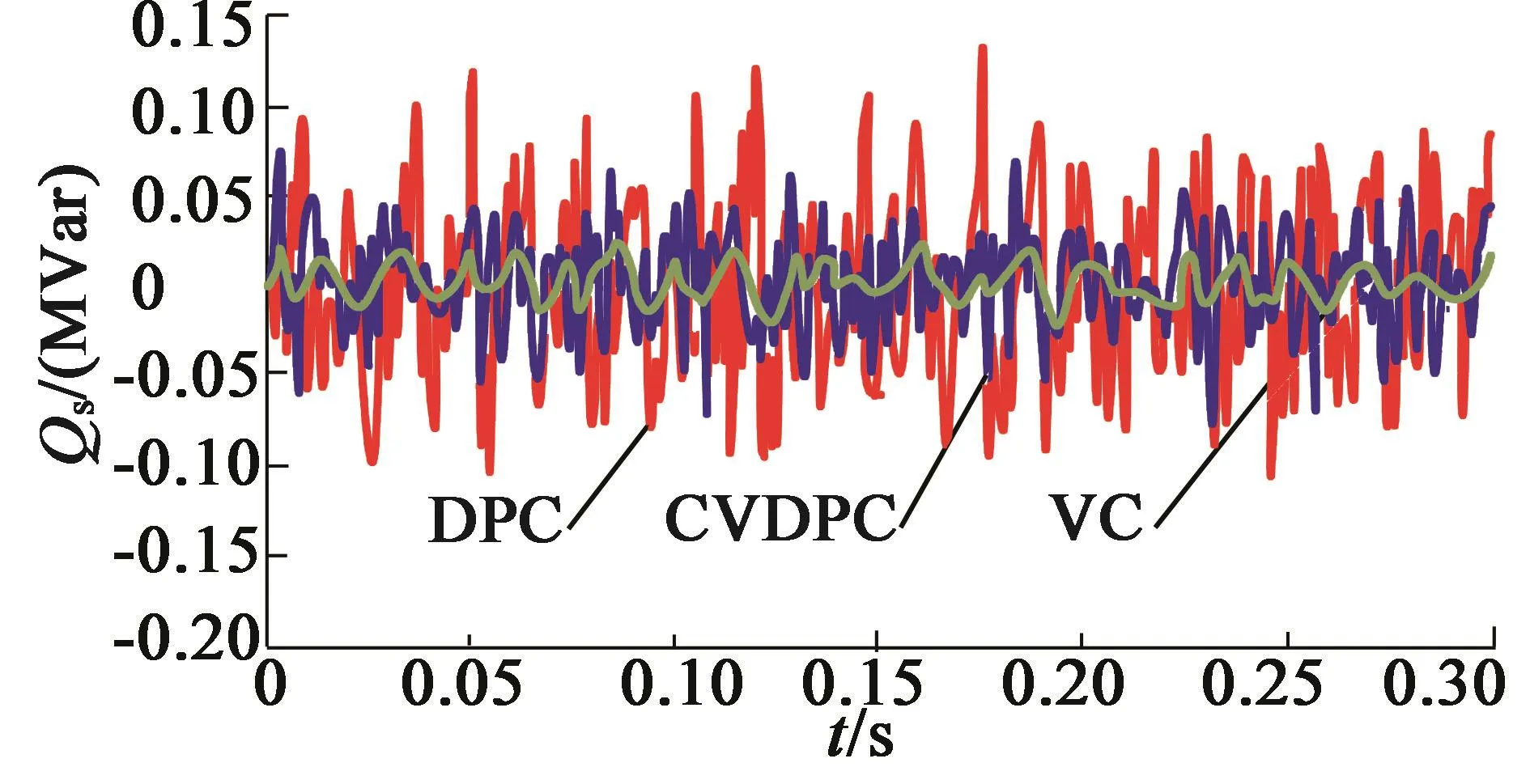
图11 定子总无功功率稳态仿真结果
图12 为3种控制方案VC、CVDPC和DPC下的定子电流波形。进一步进行FFT分析可以得到,VC下的总谐波畸变THD为1.28%,CVDPC下的总谐波畸变THD为2.1%,VC下的总谐波畸变THD为4.64%。因此,新型控制方案稳态下谐波输出性能接近VC方案,明显优于DPC方案。

图12 定子总有功功率稳态仿真结果
图13 ~图17为风速变化时3种不同控制策略的动态响应过程。其中风速在t=0.3 s时从15 m/s阶跃下降至10 m/s,DFIG转子的转速从2 220 r/min下降到1 480 r/min,同时定子总有功功率从7.58MW下降到2.81MW。当DFIG运行在次同步速度,即s=+0.2,20%的定子有功功率将通过变流器返回到电机,即Pr=-0.6 MW。从图中可以看出转子d轴电流idr在控制器的作用下从0.79 kA下降至0.3 kA,从而改变了定子有功功率输出,但转子q轴电流iqr保持不变,这意味着新型控制策略是一种解耦的控制方法。从动态响应的细节图中可以看出,新型控制策略的动态响应速度要明显快于VC,并接近DPC方法。因此具有较优的动态性能。

图13 风速突变时发电机转速仿真结果
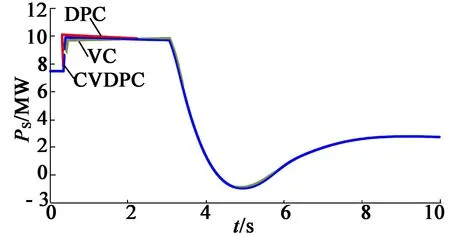
图14 风速突变时定子总有功功率仿真结果

图15 风速突变时转子总有功功率仿真结果

图16 风速突变时转子d轴电流仿真结果

图17 风速突变时转子q轴电流仿真结果
4 结 语
本文主要稳围绕着一种新型的结合矢量和直接功率控制的双馈风电机组控制策略进行了相关研究。现总结主要结论:
(1)双馈风电机组的矢量控制和直接功率控制之间存在数学本质上的共通处,基于此设计出了结合矢量和直接功率控制的新型方案。
(2)CVDPC在机组稳态运行时比DPC具有较小的功率波动和输出谐波,而在动态过程中比VC具有较快的动态响应,因此其结合了两者的优点,并通过仿真进行了验证。
参考文献
[1] LISERRE M,CARDENAS R,MOLINAS M,eyt al.Overview of multi-MW wind turbines and wind parks[J].IEEE Transactions on Industrial Electronics,2011,58(4):1081-1095.
[2] BLAABJERG F,MA K.Future on power electronics for wind turbine systems[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2013,3(1):139-152.
[3] 聂文海,周洁,霍菲阳,等.定速异步风机低电压穿越技术研究[J].电网技术,2014,38(s2):99-101.
[4] 刘波,潘巧波.大型直驱风电机组快速响应控制策略[J].电机与控制应用,2015,42(11):62-66.
[5] 年珩,程鹏,贺益康.故障电网下双馈风电系统运行技术研究综述[J].中国电机工程学报,2015,35(16):4184-4197.
[6] 唐西胜,苗福丰,齐智平,等.风力发电的调频技术研究综述[J].中国电机工程学报,2014,34(25):4304-4314.
[7] 涂娟,汤宁平.一种新型直驱式风力发电系统控制策略[J].电机与控制应用,2015,42(7):52-56.
[8] 郑景文,秦亮,刘开培.双馈式风力发电机运行与控制的数字仿真研究[J].微特电机,2016,44(1):27-33.
[9] 朱云国,张兴,谢震,等.无刷双馈风力发电机的无速度传感器矢量控制的仿真研究[J].太阳能学报,2013,34(3):496-502.
[10] 边道海,邓先明,张祥虎.基于高频注入的双馈电机无传感器控制研究[J].微特电机,2015,43(3):51-54.
[11] JABR M H,LU D,KAR C N.Design and implementation of neuro-fuzzy vector control for wind driven doubly fed induction generator[J].IEEE Transactions on Sustainable Energy,2011,2(4):404-413.
[12] LI S,HASKEW A T,WILLAMS A K,et al.Control of DFIG wind turbine with direct-current vector control configuration[J].IEEE Transactions on Sustainable Energy,2012,3(1):1-11.
[13] 高保龙,韩力,杨硕,等.无刷双馈电机新型控制策略综述[J].微特电机,2012,40(12):59-63.
[14] VIEIRAL A P J,NUNES A V M,BEZERRA H U,et al.Designing optimal controllers for doubly fed induction generators using a genetic algorithm[J].IET Generation Transmission&Distribution,2009,3(5):472-484.
[15] XU L,CARTWRIGHT P.Direct active and reactive power control of DFIG for wind energy generation[J].IEEE Transactions on Energy Conversions,2006,21(3):750-758.
[16] 孙丹,邓伦杰,孙士涛,等.双馈异步风力发电机优化预测直接功率控制[J].电工技术学报,2013,28(11):78-85.
[17] HU J,NIAN H,HU B,et al.Direct active and reactive power regulation of DFIG using sliding-mode control approach[J].IEEE Transactions on Energy Conversions,2010,25(4):1028-1039.
[18] HU J,ZHU J,YANG Y,et al.Predictive direct virtual torque and power control of doubly fed induction generators for fast and smooth grid synchronization and flexible power regulation[J].IEEE Transactions on Power Electronics,2013,28(7):3182-3194.
[19] ABAD G,RODRIGUEZ A M,POZA P.Two-level VSC-based predictive direct power control of the doubly fed induction machine with reduced power ripple at low constant switching frequency[J].IEEE Transactions on Energy Conversions,2008,23(2):570-580.
[20] VAEZ-ZADEH S,DARYABEIGI E.Combined vector and direct torque control methods for IPM motor drives using emotional controller[C]//IEEE 2nd Power Electronics Drive System Technology Conference.IEEE,2011:140-150.
[21] VAEZ-ZADEH S,SHAFAIE R.Toward a common framework for analysis of high performance controls of PMS motor drives[C]//IEEE 2nd Power Electronics Drive System Technology Conference.IEEE,2011:241-245.
[22] FARASAT M,KARAMAN E.Efficiency-optimized hybrid fieldoriented and direct torque control of induction motor drive[C]//IEEE International Conference on Electronic Machine System.IEEE,2011:1-4.
[23] BOULGHASOUL Z,ELBACHA A,ELWARRAKI E,et al.Combined vector control and direct Torque control an experimental review and evaluation[C]//IEEE International Conference on Multimedia Computation System.IEEE,2011:1-6.
