标量控制大惯性永磁同步电机的重起控制研究

王双岭，陈会鸽

(1.中原工学院信息商务学院,郑州451191;2.黄河科技学院,郑州450001)

0 引 言

相对于感应电机,永磁同步电机(以下简称PMSM)具有较高的功率密度和可靠性,同时免除了励磁调节,被广泛应用在电力传动领域[1-3]。PMSM的驱动控制多采用矢量控制方案,但是标量控制也具有简单可靠、不依赖电机参数的优点,通常和矢量控制结合使用,尤其是在电机起动过程中[4-6]。

在PMSM驱动应用中,可能会出现短时功率中断现象,例如故障切出重合闸时,失电时间可以从几个毫秒至几秒不等,这对于常规的永磁驱动系统来说,需要重新等到转速降低至零才能恢复运行,这对于大惯性PMSM往往意味将停机几分钟,这是不利于实际系统运行的。因此有越来越多的文献关注了电机驱动系统的飞车起动[7-17]。对于感应电机驱动系统,文献[7-13]使用了基于滑差信息的频率搜索法,这不适用于PMSM驱动系统,而文献[14]中的方法虽然可推广到PMSM驱动系统,但需要增加一个额外的电压传感器测量回路,增加了成本,同时可靠性降低。针对PMSM驱动系统的飞车起动问题,文献[15]通过使用单一零序电压脉冲来估计电机转速。文献[16]在文献[15]的基础上增加了一个零序电压脉冲来补偿电流采样延迟以获取更为精确的转子位置。而文献[17]提出使用一种中间零序电压脉冲插入的方法来精确对前后两个脉冲之间的转子旋转圈数计数,从而获取转速信息,但是在较低速时可能导致较大误差。由于文献[15-17]中的所涉及到的方法都需要预先知道电机参数,包括定子电阻或定子电感等,这些参数的扰动都有可能导致转速估计的误差。同时,这些方法都是针对PMSM矢量驱动控制,对于PMSM标量控制系统而言,这些电机参数通常都是未知的,所以也不适用于前述方法。文献[18-23]使用了基于高频注入的重起方案,该方案可以实现转速的宽范围估计,但是需要一个状态滤波器或观测器和对应的解调进程,因而复杂度高,计算量大,不利于工程实现。

综上,PMSM重起算法设计的难点在于PMSM由永磁体提供励磁,没有阻尼绕组将导致电机易于失去同步性,对转速估计的较小误差将导致重起过程中较大的浪涌电流。因此本文在前述文献研究基础上,设计了一种标量控制大惯性永磁同步电机的通用重起控制策略,该方法能最大限度地减小转速估计误差,同时不需要预先知道定子电感值,鲁棒性强,属于一种新型的PMSM重起算法。本文最后通过PMSM驱动试验平台对新型重起控制策略进行了试验验证。

1 传统的PMSM重起方案

在设计新型重起控制算法之前,首先对传统的电机飞车起动方案进行描述。

1.1 转速估计方法

根据文献[17],PMSM的转子速度可以通过2个零序电压脉冲构成的序列进行估计,具体原理如图1所示。由零序电压脉冲产生的电流转换到α-β坐标下为 iα和 iβ,其夹角 θI:

图1 零序电压脉冲序列速度估计原理

考虑到2个脉冲之间的时间间隔较小,因而在机械惯性的作用下,转子速度假定保持不变。因此,电机转速可以通过使用这组2个零序电压脉冲序列产生的电流进行运算得到,具体如下:

式中:tpulse为电压脉冲作用在定子绕组上的时间;τ是2个脉冲之间的间隔时间;ωr是转子转速。在选择延迟时间τ的时候,应当考虑电机额定转速,避免在τ时间内转子完成旋转一周,造成转速计算不正确,可以描述为如下形式:

式中:N为2个脉冲间隔时间内转子旋转圈数;ωreal是实际转速;ωest是估计转速。从式(3)中可以看出,ωest等于ωreal,只有N等于零才成立。故可以得到如下约束保证N等于零:

如果考虑要得到转子方向的信息,需要将上式中2π用π代替。

1.2 转子位置估计方法

在d-q同步坐标系下的PMSM的动态数学模型[18]:

式中:p为微分算子;vd和vq分别为d,q轴定子电压;id和iq分别为d,q轴定子电流;Rs为定子电阻;Ld和Lq分别为d,q轴定子电感;λf为永磁磁链;ωr为转子电角速度。当运用零序电压时,有vd=vq=0,同时tpulse一般设置为远小于时间常数τd=Ld/Rs和τq=Lq/Rs,此时可忽略定子电阻的影响,进而式(5)可以简化[17]:

通过使用拉普拉斯变换求解上式电流:

上式中,转子转速可以从式(2)中得到,tpulse为零序电压作用时间,Ld,Lq和λf为电机参数,故根据式(7)计算得到d,q轴电流后,可以估计出定子电流矢量和d轴的角度差θ0:

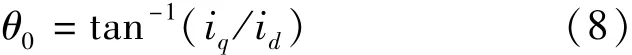
根据式(8)中得到的θ0,并结合矢量图可以得到转子位置:

式(1)至式(8)所描述的传统的PMSM测速重起方案存在以下缺点:

(1)需要事先知道电机参数Ld,Lq和λf,同时对参数依赖,将导致鲁棒性降低。

(2)该方法使用的零序电压注入为占空比为100%的PWM脉冲,占空比不可控在某些情况下将导致过流,例如当电机转速较高或定子电感较小时。

(3)电流传感器误差将产生转速估计误差,进而也可能导致重起过程中触发过流保护停机。

2 新型PMSM重起策略

在设计新的PMSM重起算法前,先做出如下假设:

(1)在PMSM失电时,控制器保持工作;

(2)控制器保存了在PMSM失电前和失电后的转速指令;

(3)控制器能快速识别失电和恢复供电。

由于工程中控制器一般由UPS供电,所以假设(1)和假设(2)成立,同时失电和恢复供电可以通过检测电路识别,因此假设(3)也成立。

2.1 转速和转子位置估计

根据前述传统控制算法,首先根据式(1)和式(2)的原理,同时满足式(4)的约束,将式(7)代入式(8)可以首先确定θ0,具体:

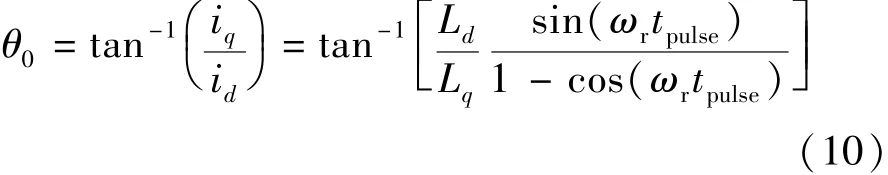
上式说明θ0是具有2个变量的函数,2个变量分别是d,q轴定子电感的比值Lq/Ld和转速与脉冲作用时间的乘积ωr·tpulse,图2为θ0=f(Lq/Ld,ωr·tpulse)函数的数值求解图。

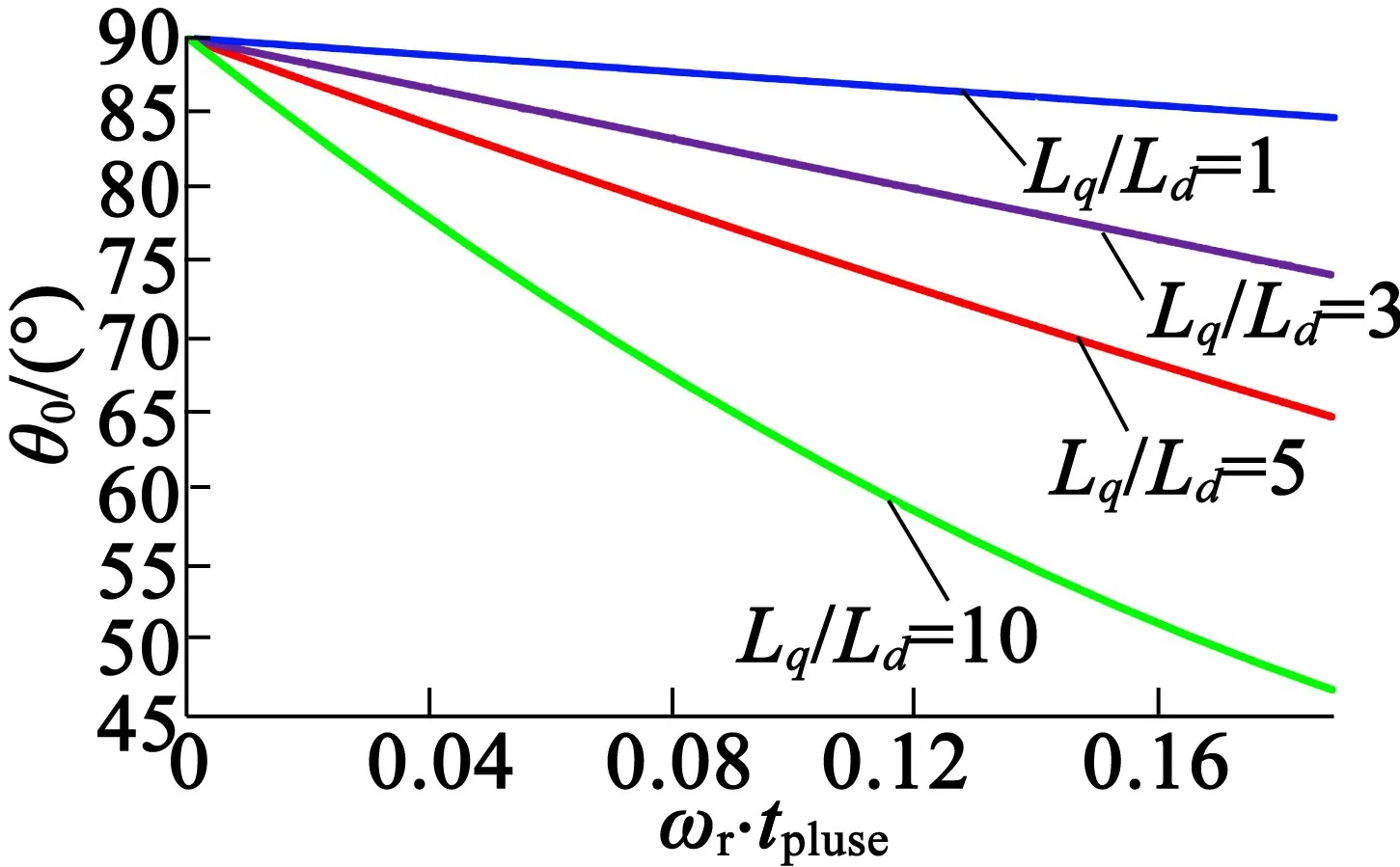
图2 函数θ0=f(Lq/Ld,ωr·tpulse)数值求解图

根据图2的结果和式(10),可以得到:对于一个较小的脉冲作用时间和一个较小的Lq/Ld比值,θ0的值接近90°。通常PMSM电机设计时将Lq/Ld比值设定小于5[24],因此将ωr·tpulse限制为0.035以下,θ0将大于 85°,若假定 θ0为 90°,则转子位置角估计误差将小于5°,将θ0=90°代入式(9)可得:

2.2 电流传感器误差分析

由于转速估计是基于电流矢量角θI,电流检测误差将导致转速估计误差,考虑到实际中电流传感器一般是有误差的,因此需要对其进行分析。将电流检测增益误差和偏置误差表示如下:

式中:iαm和 iβm为电流传感器测量得到的 α-β 坐标下电流;Δiα_error和 Δiβ_error分别为 iα和 iβ的增益误差;Δiα_offset和 Δiβ_offset分别为 iα和 iβ的偏置误差;Im为电流矢量幅值;kα和kβ为电流传感器增益误差系数;kα_offset和 kβ_offset为电流传感器偏置误差系数。 考虑到控制器一般在驱动系统运行前会校正直流偏置,所以将上式中的偏置误差忽略,从而得到:

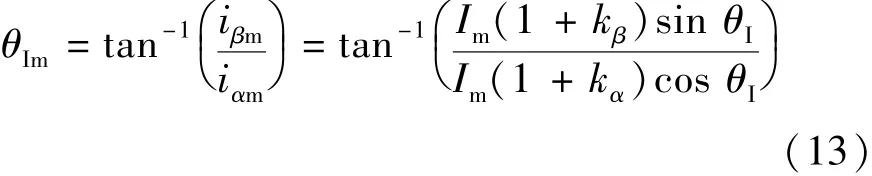
假设电流传感器有1%的检测增益误差,则基于式(13)计算得到产生的位置角误差小于0.6°,具体如图3所示。

图3 1%电流传感器误差导致的位置角误差

在图3中,横轴坐标描述了为电流矢量角θI的变化,而纵轴坐标为实际转子位置角和计算转子位置角的差异Δθ,进而最大的速度估计误差:

式中:Δθmax是最大相角误差;TSW为开关周期;Ndelay为2个脉冲之间的开关周期数目。从上式中可以看出最大的转速估计误差可以通过选择Ndelay来进行调节。换个角度,即可以通过最大容许转速测量误差系数εω来限制Ndelay如下:

上式中的上边界保证了在2个脉冲延时期间转子不会完成旋转一周。本文中选取εω=5%来设置Ndelay的下边界。

2.3 转速和转子位置估计误差量化分析

如前所述,文献[15-17]中所提出的方法需要知道电机的参数,而电机参数是可能随温度和定子电流的变化而发生扰动的。这里对Lq变化引起的误差进行量化分析,因为对于PMSM而言,Lq变化往往比Ld变化对误差影响更明显。考虑Lq变化后,式(7)可以重写:

式中:iq_actual为q轴电感增加ΔLq后的实际q轴电流,将式(16)代入式(8),可以得到:

通过将实际定子电流矢量和d轴的角度差θ0_actual和式(8)运算得到的θ0相比可计算出q轴电感参数扰动引起的转子位置角误差Δθ0_error如 下:

从数值分析来看,随着ΔLq的增加,Δθ0_error是逐渐增大的,特别当 Lq变化一倍后 Δθ0_error可达到20°,具体如图4所示。

图4 q轴电感变化引起的转子位置估计误差

此外如前所述,电流传感器误差将导致转速误差如式(14)所示,考虑转速误差后,参考式(16),可以得到如下表达式:

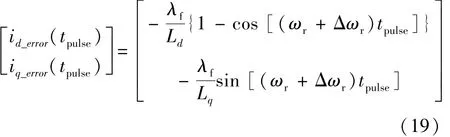
式中:Δωr是由电流传感器误差引起的转速偏差。同时考虑ΔLq引起的误差和传感器误差后可得到θ0的实际值:

经过量化分析,当ΔLq变化1倍且传感器误差达到 1%后,Δθ0_error也将达到 20°。

2.4 新型PMSM重起控制设计

在对转速和转子位置误差进行量化分析后,设计了一种新型的PMSM重起控制策略,新方法使用了3个零序电压脉冲,具体如图5所示。

图5 新方案的零序电压脉冲序列

新型PMSM重起控制实施步骤如下:

(1)首先发出第1个占空比较小的零序电压脉冲(如10%占空比),然后记录脉冲电流峰值作为后续脉冲占空比宽度的依据。

(2)在间隔时间α后(α满足式(4)),发出第2个占空比等于D1的脉冲,D1设置为使得零序电压脉冲产生的电流峰值小于额定电流值以尽量减少此电流所引起的转矩。然后利用式(1)计算电流矢量角θI1,同时结合第1个脉冲信息判断转子旋转方向。

(3)在间隔时间τ后,发出第3个占空比也为D1的零序电压脉冲。τ由式(15)限制,同时τ应该选择使转速估计误差尽量小,但实际中还必须考虑电机转速在时间τ期间不会明显变化才可以。利用式(2)和式(11)可估计转速和转子位置。

(4)如果ωr·tpulse≥0.035,则调整占空比 D1,重复步骤(2)至步骤(3),以保证转速误差范围的合理。

(5)若 ωr·tpulse＜0.035,则当定子电流降至到零后进行PMSM重起动。其中基于反电动势计算电压幅值指令,而电压相角从步骤(3)中估计得到。对于V/f标量控制器中的频率也基于步骤(3)选择。

在步骤(1)中,为了明确脉冲占空比与峰值电流的关系,可以列出表达式如下:

式中:Kslope为电流上升斜率;Eemf是由永磁磁链产生的反电动势;ΔIpulse是零序电压脉冲作用后电流的增量。这里将Kslope假定为常数,是因为脉冲作用时间很短,进而电流变化和脉冲占空比近似成线性关系,后续脉冲的占空比可按此规律调整以避免过流,同时也确保脉冲电流足够大以最大限度地减少检测误差。在步骤(3)中,存在开关周期延迟和电流采样延迟,因此引入补偿后的转子位置θcomp如下:

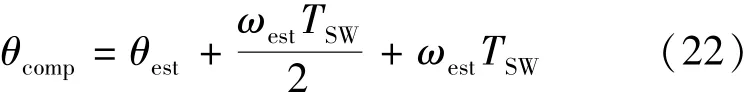
式中:θest为式(11)计算得到的转子位置。式(22)中等号右边第二项补偿了开关周期延迟,而第三项补偿了电流采样延迟。

相对于传统PMSM重起控制算法,新方案的优势体现在以下几个方面:1)新算法仅使用电机的铭牌参数,避免了复杂的电机参数测定过程;2)新算法不使用估计转速计算转子位置角θ0,故不会造成误差放大;3)新算法对于定子电感参数变化和电流传感器误差的鲁棒性较强;4)新算法可以调节零序电压脉冲的占空比,能有效地避免过流的发生。

3 试验验证

为了验证本文中的PMSM飞车起动算法,基于PMSM驱动试验平台进行了试验研究,试验平台的主体是一台12 kW的PMSM和用感应电机模拟的负载,如图6所示。PMSM的参数如表1所示。其他试验系统构成还包括由额定1 200 V/100 A的IGBT为主体的变频器、转速传感器和由DSP28335为核心的控制器,以及相关的电流和电压传感器。系统采样频率设置为5 kHz。

图6 PMSM驱动试验平台

表1 PMSM主要参数

图7为采用新型重起控制策略的PMSM飞车起动试验波形。具体的试验过程如下:首先,控制电机运行在所要测试飞车起动的目标转速;然后,将变频器的输入直流电压切断造成PMSM失电,并持续2 s,在此期间电机惯性旋转并在损耗作用下降速;最后2 s结束后,恢复变频器供电,并采用重起算法进行PMSM飞车起动。其中图7(a)和图7(b)分别为目标转速为600 r/min和2 400 r/min的重起过程,包括了传感器实测转速和估计转速波形,以及转子位置角波形和定子电流波形。从图中可以看出,估计转速和实测转速在重起算法运行后是匹配的,整个重起过程持续6.6 ms,脉冲序列设置满足了前述相关约束,验证了算法的准确性,而从定子电流波形可以看出,飞车起动过程中的冲击电流较小,验证了算法的有效性。

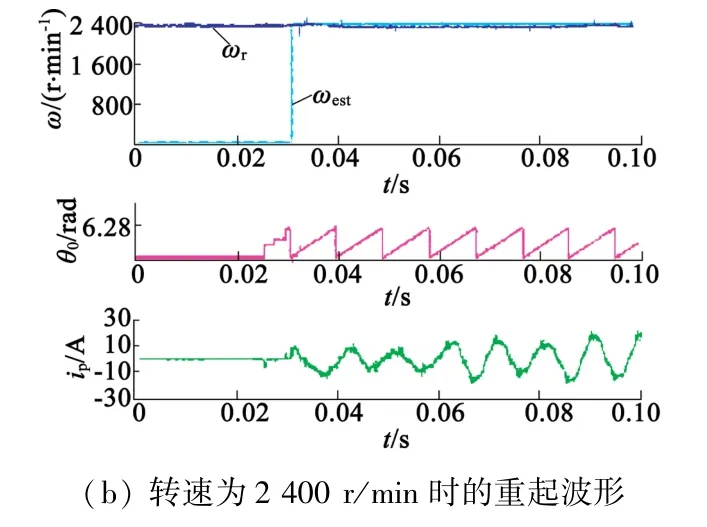
图7 PMSM重起试验波形

为了验证前述对转速误差量化分析的正确性,以及转速误差对PMSM重起的影响,进行了5%和10%转速误差下的重起试验,试验目标转速为1 200 r/min,试验波形如图8所示,包括了传感器实测转速和估计转速波形,以及转子位置角波形和定子电流波形。其中图8(a)为转速误差为5%时的重起过程,重起过程中浪涌电流25 A,PMSM重起成功。但当转速误差为10%时(图8(b)),浪涌电流最大达到35 A,触发了过流保护,导致PMSM重起失败。试验结果进一步验证了前述误差量化计算的正确性。

图8 转速误差对PMSM重起的影响

4 结 语

本文针对PMSM的飞车起动问题开展了相关研究,并设计了一种标量控制大惯性永磁同步电机的重起控制策略,可总结出以下结论:

(1)不同于传统的PMSM重起控制算法,新型控制方案仅需要电机铭牌参数就可以进行转速和转子位置估计。

(2)对电流传感器测量误差和电机参数变化引起的转速和转子位置估计误差进行了量化分析,为新型控制策略设计提供了依据。

(3)新方案可以自动调整零序电压脉冲占空比以避免过流发生,同时还可以根据额定转速和实际可接受误差范围来自动调整2个零序电压脉冲之间的时间间隔,因此提高了PMSM重起的可靠性。

(4)试验研究结果验证了在低速和高速工况下,新型控制策略都能有效地进行PMSM重起,是一种通用的PMSM飞车起动方法,适用于大惯性PMSM驱动系统。

参考文献

[1] 符晓玲,刘旭东.电动汽车用永磁同步电机滑模预测控制[J].微特电机,2015,43(11):53-56.

[2] 李东和.纯电动汽车用永磁同步电机温度场计算[J].微特电机,2016,44(1):12-16.

[3] 洪俊杰,陈思哲,郭壮志,等.基于电流预测控制的电动汽车用PMSM控制器设计[J].微特电机,2015,43(8):99-102.

[4] 张前,冯明.超高速永磁无刷电机无位置传感器半闭环启动法[J].电机与控制学报,2016,20(10):23-31.

[5] 张耀中,黄进,康敏.永磁同步电机无传感器控制及其启动策略[J].电机与控制学报,2015,19(10):1-6.

[6] 肖烨然,刘刚,宋欣达,等.基于改进滑模观测器的永磁同步电机无位置传感器I/F起动方法[J].电力自动化设备,2015,35(8):95-102.

[7] PAN H,SPRINGOB L,HOLTZ J.Improving the start and restart behavior through state recognition of AC drives[C]//Proceedings of the Power Conversion Conference-Nagaoka 1997.IEEE,1997:589-594.

[8] SUZUKI K,SAITO S,KUDOR T,et al.Stability improvement of V/F controlled large capacity voltage-source inverter fed induction motor[C]//IAS Meeting Conference Record of the Industry Applications Conference,IEEE,2006:90-95.

[9] IURA H,IDE K,HANAMOTO T,et al.An estimation method of rotational direction and speed for free-running AC machines without speed and voltage sensor[J].IEEE Transactions on Industry Applications,2011,47(1):153-160.

[10] 张德宽,张军军,乔奕玮.异步电机双向速度搜索再启动方法的研究[J].电气传动,2012,42(9):3-6.

[11] 王宏英,龚世缨.电机重起动的控制策略[J].电气传动,2013,43(7):68-71.

[12] 王书秀,吴振兴,孙乐,等.一种能量回馈的高压变频器失电跨越控制策略[J].电气传动,2016,46(8):11-15.

[13] 穆天柱,刘春松,胡炫.转速估算在高压电机变频器节能改造上的应用[J].电机与控制应用,2013,40(1):51-54.

[14] JEONG S J,PARK Y M,HAN G J.An estimation method of rotation speed for minimizing speed variation on restarting of induction motor[J].Clinical&Experimental Allergy,2011,43(6):697-704.

[15] TOSHIFUMI Y,SHINJI W,KEIICHIRO K,et al.Starting procedure of rotation sensorless PMSM at coasting condition for railway vehicle traction[J].Ieej Transactions on Industry Applications,2009,169(2):56-63.

[16] SON Y C,JANG S J,NASRABADI R D.Permanent magnet AC motor systems and control algorithm restart methods:US,US 8054030[P].2011.

[17] TANIGUCHI S,MOCHIDUKI S,YAMAKAWA T,et al.Starting procedure of rotational sensorless PMSM in the rotating condition[J].IEEE Transactions on Industry Applications,2009,45(1):194-202.

[18] 王莉娜,郝强.基于高频方波信号注入的PMSM无传感器低速运行研究[J].电气传动,2015,45(6):20-25.

[19] 董晨露,陈涛.电机车IPMSM高频脉振电压注入法转子位置检测[J].电机与控制应用,2015,42(8):67-71.

[20] LIN T C,ZHU Z Q.Sensorless operation capability of surfacemounted permanent magnet machine based on high-frequency signal injection methods[J].IEEE Transactions on Industry Applications,2015,51(3):2161-2171.

[21] LIU J M,ZHU Z Q.Novel ensorless control strategy with Injection of high-frequency pulsating carrier signal into stationary reference frame[J].IEEE Transactions on Industry Applications,2014,50(4):2574-2583.

[22] KIM S,HA J I,SUL S K.PWM switching frequency signal injection sensorless method in IPMSM[J].IEEE Transactions on Industry Applications,2012,48(5):1576-1587.

[23] MURAKAMI S,SHIOTA T,OHTO M,et al.Encoderless servo drive with adequately designed IPMSM for pulse-voltage-injection-based position detection[J].IEEE Transactions on Industry Applications,2012,48(6):1922-1930.

[24] 刘奇林,沈启平.车用高功率密度永磁同步电机设计及试验研究[J].电机与控制应用,2016,43(1):88-94.