双凸定子极无轴承开关磁阻电机数学模型

杨 艳，吴 旭，李 鹏

(南京邮电大学,南京210003)

0 引 言

开关磁阻电机(以下简称SRM)的理念在19世纪就已经被提出,但当时采用的是机械开关,其可靠性和机电能量转化效率十分低下。直到20世纪60年代,因电子计算机以及功率电子的发展成熟,使得换相式供电成为可能,开关磁阻电机才得以快速发展[1]。开关磁阻电机结构简单、运行效率高、容错能力强,并能实现超高速运行,因此具有广阔的应用前景。

与许多其他电机一样,当开关磁阻电机的运行速度达到一定极限时,电机中的机械轴承会被严重磨损,需要定期人为维护,这在一定程度上限制了电机的运行转速。20世纪90年代,人们提出了无轴承开关磁阻电机(以下简称BSRM)的概念。目前,对BSRM的研究主要集中在以下领域:数学模型、控制策略、功率变化器、电机绕组结构和本体设计等研究内容。

在BSRM领域,传统12/8双绕组电机很好地实现了电机悬浮,然而转矩绕组与悬浮绕组之间的强耦合使得该电机的控制算法较为复杂[2-5],需要设定附加条件才能求得主绕组电流和悬浮绕组电流,并且需要事先将参数存储在控制系统的存储器中,这在一定程度上降低了系统性能;韩国学者提出的BSRM具有不等宽的定子极,实现了转矩与悬浮力之间的解耦控制[6-7]。该类电机的部分定子极被用来提供悬浮力,不产生转矩,降低了电机功率密度。

国内研究人员提出了一种新型BSRM[8],该电机的定子具有双凸极结构,即悬浮齿极与转矩齿极,因此也被称作双凸极BSRM。在悬浮绕组与单相转矩绕组同时导通期间,非导通相齿极中存在大量磁通,不可忽略,增加了推导电机数学模型的难度。本文先介绍了该电机的悬浮原理,接着建立了电机有限元仿真模型,并根据电机磁通分布图建立了等效磁路图。最后在忽略磁饱和的情况下,基于虚位移法[9]推导出该电机的数学模型,并利用有限元仿真证明了数学模型的合理性,为之后的电机控制提供了理论依据。

2 基本原理

图1为双凸极BSRM结构示意图。该电机转子与传统12/8双绕组BSRM相同,而定子包括悬浮齿和转矩齿。4个等间隔排列悬浮齿从定子轭伸出,每个悬浮齿再伸出3个转矩齿。

图1 双凸极BSRM结构示意图

在双凸极BSRM中,4个悬浮绕组独立控制,改变悬浮绕组电流以产生不对称磁密,从而提供悬浮力。悬浮绕组不参与换相操作,这就简化了电机的悬浮力控制。同传统12/8双绕组结构BSRM一样,每4个转矩齿相互串联,构成一相,如图中所示的A相绕组。在单相导通模式中,三相绕组各自导通15°,以产生连续的转矩。

3 悬浮力数学模型

3.1 有限元仿真模型

图2是双凸极BSRM的有限元2D仿真模型,电机的具体尺寸参数如表1所示。

图2 双凸极BSRM有限元2D仿真模型

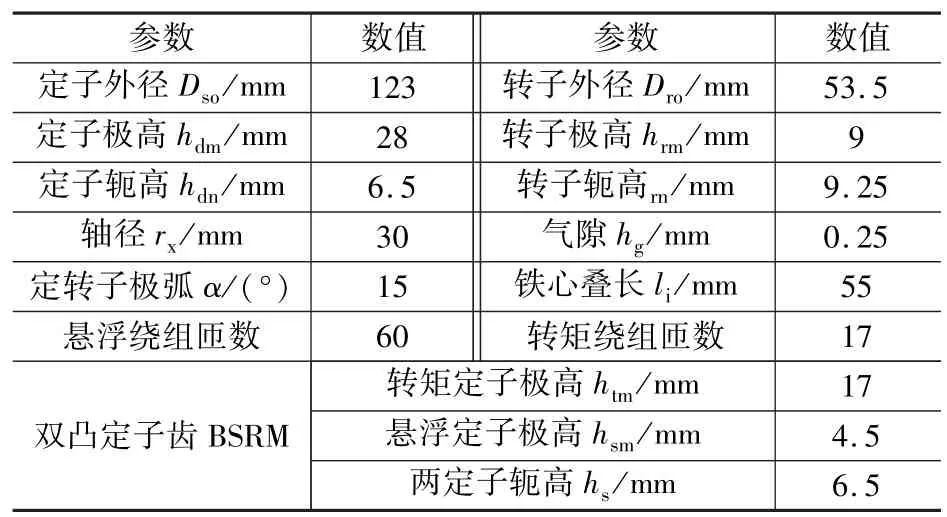
表1 双凸极BSRM结构参数

当A相绕组及4个悬浮绕组同时通电流时,磁通分布如图3所示。从中可以看出,A,B相齿极中都通有磁通,而C相齿极中几乎没有磁通。这是因为在A相导通期间,A,B相的定子齿极与转子齿极存在重叠区域,磁阻较小,而C相齿极始终对准转子齿槽,磁阻较大。在建立等效磁路图时,需要同时考虑A,B相磁通,可以忽略C相磁通。

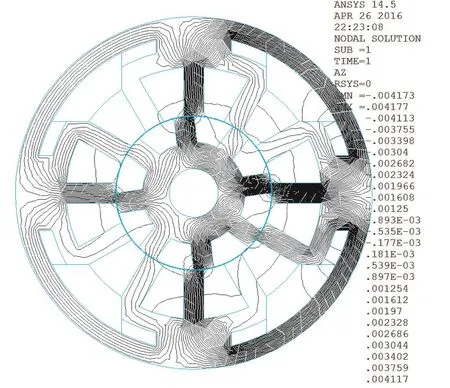
图3 电机磁通分布图

3.2 等效磁路

A相绕组导通时该电机的等效磁路图如图4所示。图中包含8个支路,计及A,B相磁通。Nsis1为悬浮绕组磁动势,Nmim为转矩绕组磁动势,Pi表示气隙磁导,φi表示磁通。

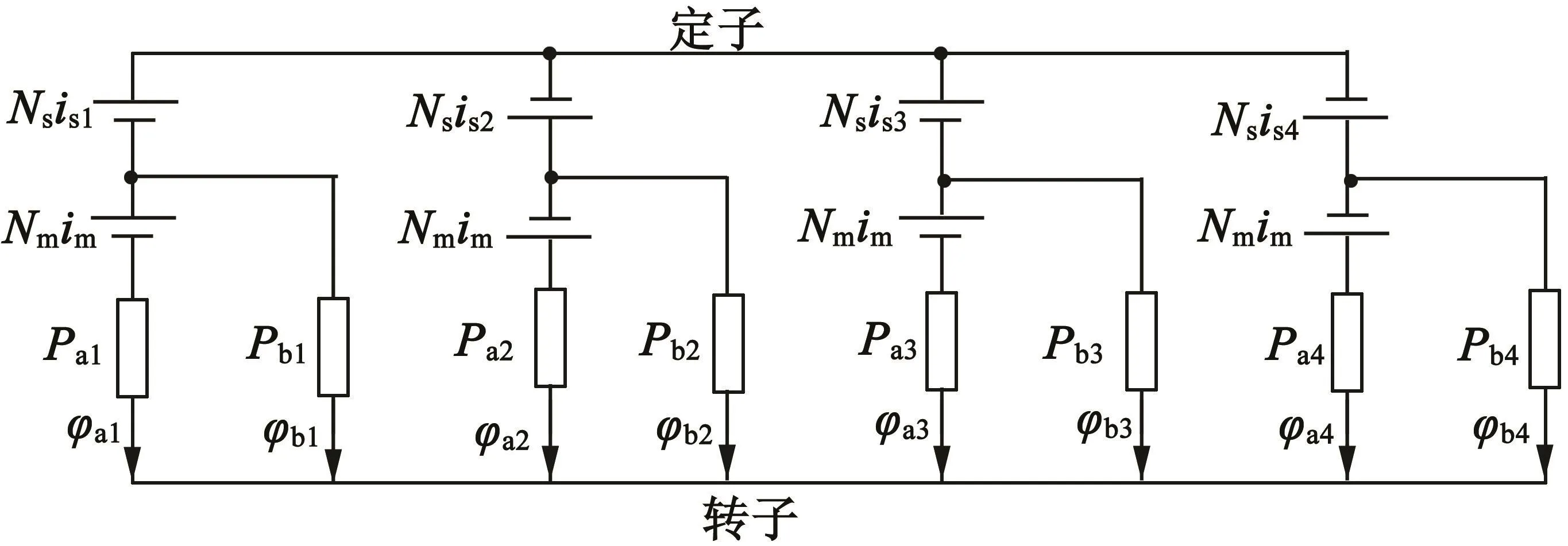
图4 电机等效磁路图

根据磁路基尔霍夫定律及磁场高斯定律可列方程组:

由此可以得到磁通表达式:

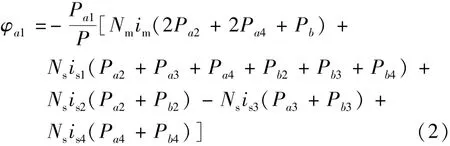
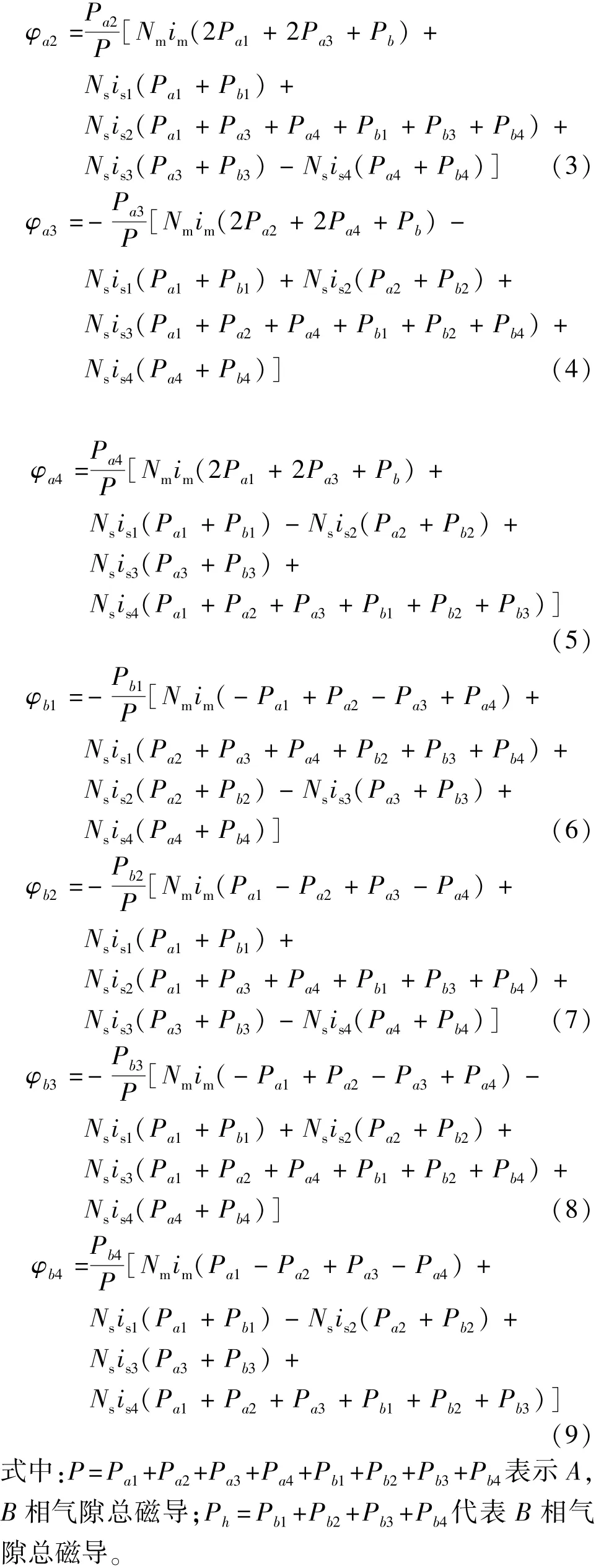
3.3 磁导计算

通常情况下,边缘磁通路径的长度远远大于气隙长度,因此边缘磁导很小。为了简化推导过程,忽略边缘磁导,即忽略边缘磁通。在A相绕组导通区间内,A相定子齿极与转子齿极的重叠区域面积增加,B相定子齿极与转子齿极的重叠区域面积则在减小,因此在忽略边缘磁导时,图4中的等效磁路不会出现磁导为零的情况。在忽略边缘磁导时,A相定子齿极下的磁导计算公式:

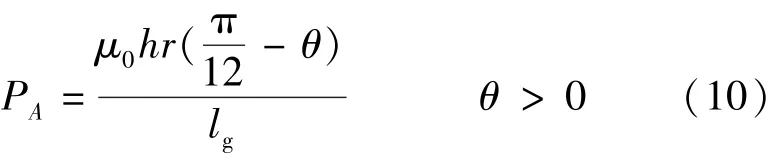
式中:μ0为真空磁导率,h为电机轴长,r为转子外径,θ为转子位置,lg为气隙长度,c为常数1.49。在考虑转子径向位移式,Pa1,Pa2,Pa3,Pa4中的lg用lg±α,lg±β 来代替,而 Pb1,Pb2,Pb3,Pb4中的 lg用 lg-3α/2+β/2,lg+α/2-3β/2,lg+3 α/2-β/2,lg-α/2+3β/2代替。

在计算转子位置角时,通常以导通相为参考相。例如,在A相导通期间,转子齿极偏离A相齿极θ角度,则转子齿极偏离B相齿极的角度为π/12-θ。因此在计算B相齿极下的磁导时,需要使用π/12-θ替代式(10)中的θ,因此在A相导通期间,B相齿极的磁导计算公式如下:

3.4 悬浮力计算

根据式(2)～式(9),悬浮绕组和转矩绕组中的磁链分别:

根据ψ=Li可以求得绕组间的自感与互感,即5×5的电感矩阵L:

则磁场储能W:

根据机电能量转化原理,可求得α方向上悬浮力:

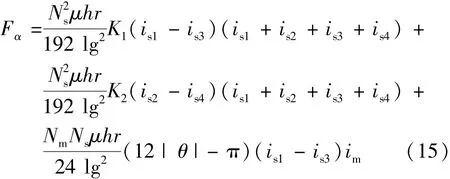
用同样的方法也可以推导出β方向上的悬浮力公式:

下面将验证上述计算公式的合理性。

3.5 仿真验证

由于悬浮绕组匝数为60匝,相对于转矩绕组较大,并且悬浮力计算公式中存在绕组匝数Ns的平方项,因此悬浮电流的细小变化都会引起悬浮力的较大变化。为了验证悬浮力计算公式的合理性,图5～图7在(-15°,0°)范围内比较了数学模型与有限元分析结果,其中横轴表示转子位置,纵轴表示α正方向悬浮力。图5中,转矩电流设定为1 A,α正方向悬浮电流分别取1 A,1.1 A,1.2 A;图6中,转矩电流设定为3 A,α正方向悬浮电流分别取1 A,1.1 A,1.2 A;图7中,转矩电流设定为5 A,α正方向悬浮电流分别取1 A,1.1 A,1.2 A。

图5 磁悬浮数学模型验证(im=1 A)

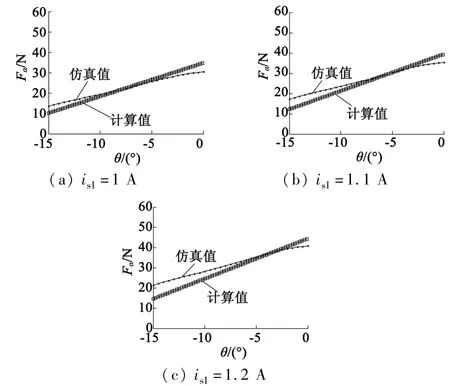
图6 磁悬浮数学模型验证(im=3 A)

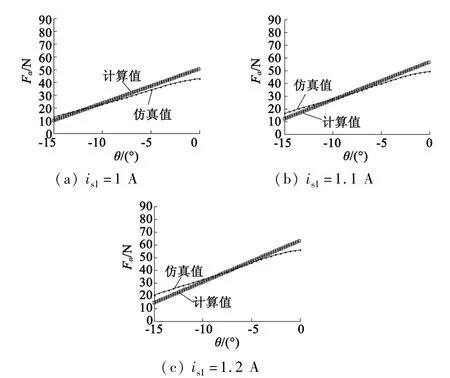
图7 磁悬浮数学模型验证(im=5 A)

由图5～图7可知,本文提出的悬浮力数学模型可以较好地反映电机悬浮特性。根据式(15)、式(16)可知,电机悬浮力与悬浮电流及转矩电流有关。在转矩电流一定时,通过改变悬浮电流可以改变电机悬浮力大小。通过比较结果可以看出,本文提出的数学模型与有限元仿真结果具有较好的一致性,可以满足工程上的控制精度要求。

4 转矩数学模型

根据文献[8]可知,双凸极BSRM实现了转矩与悬浮力之间的解耦控制,因此在推导转矩数学模型时,忽略悬浮绕组对转矩的影响。依据虚功法[9],可以推得电感上升区间内的转矩公式:

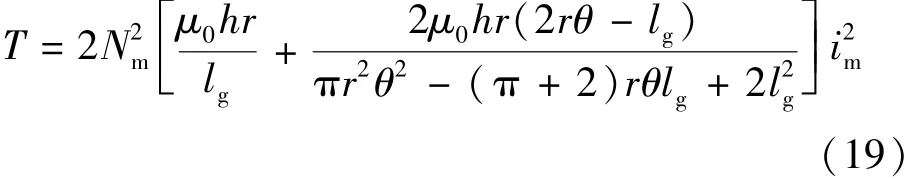
同理,电感下降区域:

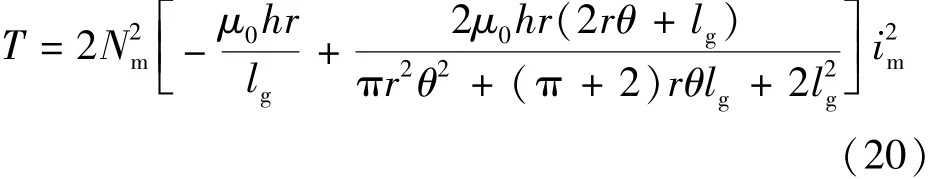
图8给出了电磁转矩Te有限元分析值与数学模型计算值的比较结果,其中纵轴表示电磁转矩,横轴表示转子位置角。

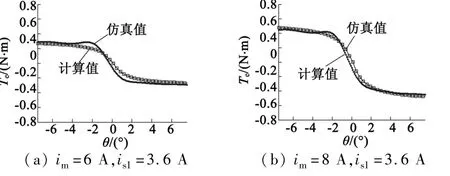
图8 电磁转矩比较

5 结 语

本文根据双凸极开关磁阻电机磁通分布特点,推导了电机的悬浮力数学模型;根据悬浮力与转矩之间的解耦特性,给出了转矩数学模型。同时利用有限元仿真实验验证了数学模型的合理性,为电机的控制策略提供了理论依据。

参考文献

[1] 吴红星.开关磁阻电机系统理论与控制技术[M].北京:中国电力出版社,2010.

[2] TAKEMOTO M,CHIBA A,FUKAO T.A new control method of bearingless switched reluctance motors using square-wave currents[C]//Power Engineering Society Winter Meeting.IEEE,2000(1):375-380.

[3] TAKEMOTO M,CHIBA A,FUKAO T.A method of determining the advanced angle of square-wave currents in a bearingless switched reluctance motor[J].IEEE Transactions on Industry Applications,2001,37(6):1702-1709.

[4] TAKEMOTO M,CHIBA A,SUZUKI H,et al.Improved analysis of a bearingless switched reluctance motor[J].IEEE Transactions on Industry Applications,2001,37(1):26-34.

[5] TAKEMOTO M,CHIBA A,SUZUKI H,et al.Radial force and torque of a bearingless switched reluctance motor operating in a region of saturation[J].IEEE Transactions on Industry Applications,2004,40(1):103-112.

[6] PARK J H,LEE D H,AHN J W.Novel bearingless switched reluctance motor with hybrid stator poles:concept,analysis,design and experimental verification[C]//The Eleventh International Conference on Electrical Machines and Systems,2008:3358-3363.

[7] LEE D H,WANG H,AHN J W.Modeling and control of novel bearingless switched reluctancemotor[C]//IEEE Energy Conversion Congress and Exposition.IEEE,2009:276-281.

[8] 杨艳,刘泽元,邓智泉.一种新型无轴承开关磁阻电机性能分析[J].微特电机,2014,42(11):14-17.

[9] 杨刚.无轴承开关磁阻电动机的基础研究[D].南京:南京航空航天大学,2008.