量子力学中的量子化
2017-05-13付亚玲
付亚玲
摘 要:由于经典理论已不能确切描述量子现象,使得我们不得不改造经典力学使其适应“全新”的量子现象,即建立新的量子力学。为此,我们研究量子化在量子力学中的应用,以线性谐振子为例用薛定谔的波动力学和海森堡的矩阵力学来说明量子化过程并提出了新的认识。
关键词:量子力学 ;量子化
中图分类号:G63 文献标识码:A 文章编号:1673-9132(2017)13-0181-02
DOI:10.16657/j.cnki.issn1673-9132.2017.13.111
一、 量子力学的发展过程
20世纪人类文明发展的一个重大飞跃就是量子力学的创立。 描述微观世界结构,运动与变化规律的物理科学科—量子力学。它引发了一系列划时代的科学发展与技术发明,对人类社会的进步做出了重要的贡献。
19世纪末当一系列经典理论无法解释的现象一个接一个的发现时(黑体辐射,光电效应,原子光谱,原子的稳定性等)。德国物理学家普朗克为了解释热辐射能谱提出了一个大胆的假设:在热辐射的产生与吸收过程中能量是以最小单位,一份一份交换的。但这个能量量子化的假设不仅强调了“经典”谐振子能量的不连续性,而且与辐射能量和频率无关由振幅确定的基本概念直接相矛盾,无法纳入任何一个经典范畴。
1923年4月,美国物理学家康普顿发表了康普頓效应。按经典波动理论,静止物体对波的散射不会改变频率。而按爱因斯坦光量子说这是两个“粒子”碰撞的结果。光量子在碰撞时不仅将能量传递而且也将动量传递给了电子,使光量子说得到了实验的证明。
1924年,法国物理学家德布罗意提出了表征波粒二象性的爱因斯坦——德布罗意关系: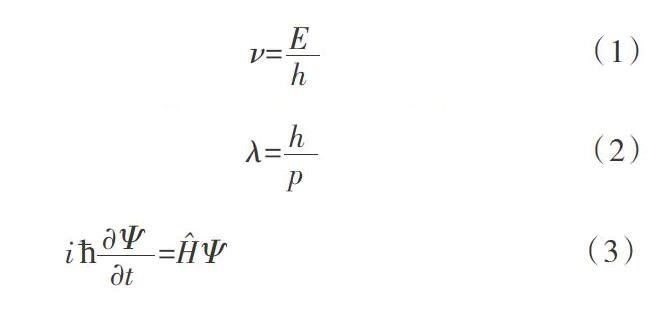
将表征粒子性的物理量能量、动量与表征波动性的频率、波长通过一个常数(普朗克常量)相联系。
1925年,德国物理学家海森堡和波尔,建立了矩阵力学。1926年,奥地利科学家薛定谔提出了薛定谔方程:
给出了波动力学。后来,薛定谔证明了这两种理论是等价的。物理学家将矩阵力学与波动力学统一起来,统称量子力学。
二、 量子力学中的量子化
“量子化现象”是指状态的不连续性,例如绕原子核运动的电子只能处于一系列不连续的能量状态上,而不能处在两个连续状态之间的状态上。量子理论是我们熟悉的,但我们需要探索的是更深层次的量子化理论的根源。这就需要我们建立新的量子力学。当然,量子力学的建立不是凭空想象的,我们仍需依靠成熟的经典力学的理论。可是实践证明,经典理论不能确切描述量子现象,这使得我们不得不改造经典力学使其适应“全新”的量子现象,即建立新的量子力学。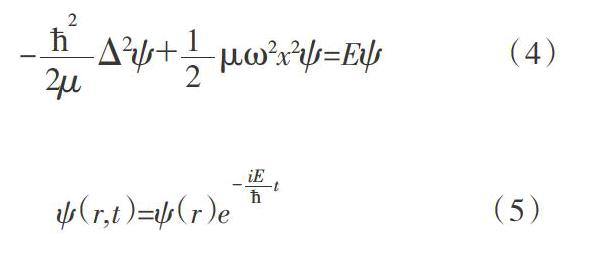
下面以线性谐振子为例用薛定谔的波动力学和海森堡的矩阵力学来说明理论上的量子化过程。
(一)波动力学
薛定谔在1926年发表的波动力学成果中,确立了波函数的变化规律,并提出了薛定谔方程,而线性谐振子的定态薛定谔方程为:
因此,能量不是连续的。薛定谔在成熟的经典力学的理论基础上,把物质波概念应用于束缚粒子建立了一种新的模型。所以只要电子处在一定的态上,它就不会向外辐射光。
(二)矩阵力学
1925年,海森堡从一些可直接观察的物理量出发,应用数学中的矩阵,找到了解释微观物理基本过程的最主要的表达方式——矩阵力学。
定义:“产生算符”
三、结语
在经典物理中,粒子性和波动性是截然分开的。量子力学与经典力学相比较而言,量子力学适用的范围更为广泛,而经典力学是这种更广泛理论的极限情况。然而,经典力学不适用于微观粒子的说法是不妥当的。若粒子的运动符合上面提出的条件,仍然可以运用经典力学去描述微观粒子的运动。我们用普朗克常量划分经典力学与量子力学的界限。如果表征粒子运动的方程中不出现普朗克常量,则量子现象可不考虑,即可应用经典力学。若出现普朗克常量,则需考虑量子力学。换句话说,可以认为经典力学是量子力学在时的极限。也就是说,在微观世界物质运动的状态没有连续性。
参考文献:
[1] Allen C.Hirshfeld,Peter Henselder,李培廉.量子力学教学中的形变量子化(I)[J].数学译林, 2003(2):141-147.
[2] 胡光华. 量子力学中的几何、代数与拓扑方法[J].国外科技新书评介, 2007(8)13-14.
[ 责任编辑 杜建立 ]
