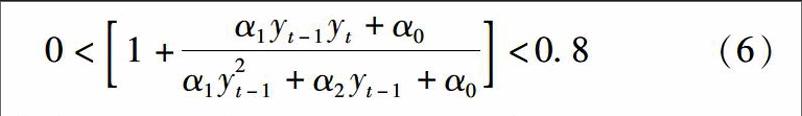经济发展与环境污染脱钩理论及EKC假说的关系
2017-05-13夏勇钟茂初
夏勇 钟茂初
摘要 脱钩理论与EKC假说,两者都描述了经济发展与环境污染之间的动态关系,其中,脱钩理论揭示了经济发展与环境压力是否同步变化的关联,而EKC假说先于脱钩理论出现,并阐述了环境污染随着经济发展水平呈现出的非线性关系。本研究基于脱钩理论与EKC假说的理论内涵,首先通过数理模型的推导,得到了二者的内在联系,并运用一阶差分GMM方法对此进行实证检验。基于数理分析和一阶差分GMM估计的实证结果显示,脱钩理论与EKC假说均呈现出先上升后下降的倒“U”型曲线特征,且相对脱钩与绝对脱钩的临界点正好对应于EKC的拐点。其次,结合二者的关联,本研究将人均GDP水平加入脱钩类型的判定标准,在传统脱钩状态分类的基础上,以EKC拐点处所对应的人均GDP水平,以及数值为0.8的脱钩弹性系数为两条分界线,进一步将城市的经济发展与环境污染脱钩关系类型划分为6种形态,分别为“高收入未脱钩”、“低收入未脱钩”、“低收入相对脱钩”、“高收入相对脱钩”、“低收入绝对脱钩”和“高收入绝对脱钩”。最后,本研究将理论部分所做的推导以及脱钩的象限划分应用于实际的城市脱钩案例研究中,并依据一阶差分GMM的回归结果,将中国271个地级城市的经济发展与污染排放的脱钩状态进行了归类。对2004-2013年中国271个地级城市的经验分析表明,近50%的城市尚处于“低收入未脱钩”和“低收入相对脱钩”状态,意味着中国地级城市发展不平衡,且城市内部的脱钩发展与经济发展不匹配问题突出,这些城市在未来的绿色脱钩建设过程中将长期面临着“保增长”和“促脱钩”的双重任务。
关键词脱钩理论;EKC假说;发展一污染关系类型;绿色脱钩城市
中图分类号 F205 文献标识码 A 文章编号 1002-2104(2016)10-0008-09 doi:10.3969/j.issn.1002-2104.2016.10.002
在现有发展模式与生态承载力的约束下,经济增长一般会伴随着污染排放。但经济增长率与污染排放变化率并不必然表现为同比例的变化关系:有的时候经济增长率快于污染排放变化率,而有时又会相反。为解释经济增长与污染排放是否同步变化的关联性,脱钩理论应运而生,并渐渐成为研究城市可持续发展的工具。但不同“底子”的城市可能处于相同的脱钩状态,若单纯以脱钩弹性系数判断城市的绿色发展或可持续发展状况,便不能准确区分城市的类型与发展阶段。在脱钩理论产生之前,学术界往往用环境库兹涅茨曲线(Environmental Kuznets Curve,EKC)描述环境污染与人均收入之间倒“U”型的关联性。EKC假说也得到越来越多的学者的验证。结合上述两个理论认识可知,EKC假说描述了经济发展与资源环境负荷的非线性关系,而脱钩理论解释了二者在可持续发展过程中的同步性(或滞后性)。若能将EKC假说与脱钩理论有效地结合起来,则可通过探讨经济发展与环境污染的绝对变化和相对变化情况,判断城市的脱钩状态是否滞后于经济增长,最终为城市的绿色发展提供改进方向。
1文献综述
OECD将经济增长与工业污染排放之间是否同步变化的关系描述成“脱钩”,并将末期的污染排放与GDP之比除以基期的污染排放与GDP之比设置为“脱钩指数”。OECD脱钩指数的提出使得经济增长与工业污染排放的相关关系得以量化,脱钩理论也因此很快成为衡量地区经济发展模式与可持续性的工具。盖美等在此基础上构建了综合脱钩指数,并用资源脱钩指数和环境脱钩指数的算术平均和表征。该综合指数拓展了DSR(Drivingforce-State-Response,驱动力一状态一响应)分析方法中状态指标的内容,弥补了以往只单纯探究经济增长与资源消耗或与环境污染脱钩关系的缺陷。但该指数也仅基于简单的算术平均加总而得,没有根据不同城市、不同经济发展水平区分资源消耗和环境污染的权重。
随着脱钩理论的进一步发展,有学者发现脱钩指数会随着基期选择的不同而发生改变,进而无法准确判断经济增长与资源环境的脱钩状态。为消除基期选择上的误差,Tapio构建了脱钩弹性系数。该弹性系数由CO2排放变化率与交通运输变化率之比,同时乘以交通运输变化率与经济增长率之比而得。这种分解方法便于更深入探究经济增长与污染排放脱钩的内在成因。但Tapio将资源环境负荷缩小为交通运输产生的CO2排放量的做法,显然没有更加全面地考虑到其他污染排放与经济增长的关联性。孙耀华和李忠民针对上述不足进行了相应的尝试。他们将Tapio两组中间变量的乘积变成三组中间变量的乘积,进而将脱钩细分为工业减排脱钩、工业节能脱钩和工业发展脱钩。这种由三组中间变量的乘积构建的脱钩弹性指标,实质上是对Tapio弹性指标“因果链”的分解与组合,对于深入研究不同产业、不同部门以及不同城市的环境压力与经济增长脱钩是一次有益的尝试。
EKC假说是由Grossman和Krueg&首先提出,用于描述环境污染与人均GDP水平之间的倒“U”型曲线关系。该假说指出,在经济增长初期,环境污染会伴随着人均收入的增加而提高,但是从中长期来看,在经济活动的结构效应和技术效应以及政府环境规制的共同作用下,环境污染会逐渐下降。倒“U”型的EKC假说得到诸多学者的验证。一些学者将环境资源视为生产要素,认为环境污染的下降是由技术或人力资本对环境资源要素的替代所引起的;还有一些学者认为环境污染是生产的负外部性体现,当技术水平、政府环境规制随着经济发展水平的提高而增强时,这种负外部性减弱,环境污染随之下降。当然,EKC假说的真实性也受到一些质疑。一些学者认为不同国家或地区的经济增长所引致的环境污染存在“异质性”和“空间相关性”,并且不同的样本区域及计量模型也会导致不同的曲线结果。因此,要么出現了由于人均GDP二次项系数显著造成EKC存在的假象,要么不存在单一的且适合所有地区及所有污染物的倒“U”型曲线关系。
综上所述,EKC假说先于脱钩理论出现,两者既有内在的联系,也有明显的差异。首先,EKC假说解释的是环境污染与人均收入之间的倒“U”型曲线关系,而脱钩理论描述的是经济增长与污染排放是否同步变化的关联性。其次,EKC假说以人均GDP和环境污染的截面数据为考察对象,探究二者在某一绝对量上的非线性关系;但是脱钩理论往往以弹性系数分析法为研究框架,侧重分析经济增长与污染排放的时间序列数据,这就决定了脱钩弹性指标只能描述经济增长与污染排放的变化速度,却忽视了二者的绝对变化量。最后,城市的环境污染受到人口规模、产业结构、资源禀赋以及地理区位等的影响,但EKC假说和脱钩理论均只能解释经济发展水平与环境污染之间的非线性关联,二者均没有解释经济增长影响环境污染的作用机制是什么。
基于此,本研究将从以下三个方面对现有研究进行拓展:之一,结合EKC模型和Tapio脱钩弹性系数模型,拟通过数理推导得出二者的内在联系,即相对脱钩与绝对脱钩的临界点正好对应于倒“U”型EKC的拐点。之二,构建以人均GDP为横轴、脱钩弹性系数为纵轴的平面直角坐标系,然后将人均GDP加入脱钩的判定标准,进而对脱钩状态进行全新归类。之三,通过动态面板数据模型实证检验EKC假说与脱钩理论内在联系的合理性,并根据一阶差分GMM方法的回归结果得到EKC的拐点处所对应的人均GDP水平。
2理论分析与模型推导
2.1脱钩理论
脱钩理论阐述的是经济增长与工业污染排放之间是否具有同步变化的关系。其函数表达式为
(1) 式中,e为脱钩弹性系数;P表示工业污染排放量;△P由本期污染排放量减去上期污染排放量而得,表示污染排放变化量;l,是地区生产总值,即GDP;△Y为相邻两期GDP之差。Tapio依据弹性系数值的大小以及△P和△Y的符号标准给出了8种脱钩状态,分别为相对脱钩、绝对脱钩、衰退脱钩、扩张负脱钩、强负脱钩、弱负脱钩、增长连结和衰退连结(见表1)。
2.2EKC假说
EKC假说描述的是环境污染随着人均GDP水平的增加而出现的倒“U”型关系。已知EKC曲线为人均GDP及其二次项的函数形式,即
Pit=α1y2it+α2yit+α0 (2)
式中,Pit表示城市i第t年的污染排放量;yit表示城市i第t年的人均GDP水平;假设人口增长率为0,且城市i的人口数量为ni,则有Yit=niyit,同时也有△Y=△ni△y,此处Y表示地区生产总值;α1和α2为人均GDP的二次项和一次项系数;α0为除人均收入水平以外影响环境污染的因素的集合,主要包括产业结构、经济开放度、科技投入、环境规制等,以下考虑到简化模型与数学推导需要,本研究视其为常数项。式(2)中用yit及其二次项来考察EKC的存在性,若α1<0且α2>0,则满足倒“U”型曲线关系;反之则为“U”型。鉴于经济增长与环境污染的现实意义以及经典EKC假说的广泛适用性,本研究设定EKC为倒“U”型特征。
2.3脱钩理论与EKC假说的关系推导
对脱钩模型式(1)和EKC模型式(2)进行联立方程组,求解可得:
(3)
情形一,绝对脱钩。此时约束条件有△P<0,△Y>0,e<0。将式(3)代入约束条件,可得
(4)
由于本研究考察的是长期内的经济增长与污染排放的脱钩状态,因此可以将时间t看成是一个趋近于无穷大的常数。当t→+∞。时,可以对式(4)的两边取极限值,此时有:
(5)
综合式(4)和式(5)的结果可知,若要保证经济增长与污染排放的绝对脱钩,则连续两年的人均GDP之和要超过-α2/α1的水平,且当年的人均GDP水平必须跨过EKC的拐点-α2/2α1。
情形二,相对脱钩。此时要求△P>0,△Y>0,0 (6) 从不等式左边来看,由于α1<0,在假设经济增长速度为正的情况下,必然有yt+yt-1<-α2/α1。同理,对该不等式两边求极限,可得yt<-α2/α1。从不等式右边来看,为简化计算,此处令常数项α0=0,同时对不等式两边求极限值,可得如下结果: (7) 综合不等式(6)左右两边的测算结果来看,只有当人均GDP水平满足-α2/6α1 结合情形一和情形二的结果可知,若追求城市经济增长与环境污染的绝对脱钩,那么当年的人均GDP水平必须跨过阈值点-α2/2α1,并且保证连续两年的人均收入水平在-α2/2α1的水平之上;若保持城市经济增长与资源环境的相对脱钩,则当年的人均GDP水平必须满足(-α2/6α1,-α2/2α1)的区间。由此可以看出,相对脱钩与绝对脱钩的临界点所对应的人均GDP位于-α2/2α1處,也即EKC的拐点处所对应的人均GDP水平。 2.4脱钩状态的象限划分 Tapio脱钩弹性系数同时受到经济发展水平和污染排放量的影响,这表明同一脱钩状态也会存在经济发展水平或污染排放水平的差异。比如,经济发展水平较高的城市可以通过不断降低污染排放达到相对脱钩或绝对脱钩状态,同时,经济发展水平较低的城市由于其工业水平不高而导致污染排放较少,最终也能达到与经济发展水平较高城市相同的脱钩状态。因此,不能单纯地以脱钩系数大小作为判断城市可持续发展的依据。比较合理的做法是将人均GDP水平加入脱钩状态的判定标准,综合考察城市“经济发展一环境污染”的脱钩状态。基于此,在分析脱钩理论时,可以将城市的经济发展水平作为一个参考系,构建一个以人均GDP为横轴、脱钩弹性系数为纵轴的平面直角坐标系,其中,横轴和纵轴分别用y和e表示。
在横轴当中,假设存在一个人均GDP的门槛值y*,在y*左侧,表示经济发展水平较低的区域,与此相对应,y*的右側则为经济发展水平较高的区域。结合Tapio脱钩弹性系数的划分原则以及人均GDP的门槛值y*,本研究以EKC拐点处的人均GDP(也即y*)和数值为0.8的脱钩弹性系数为临界点,分别作一条垂直于横轴和纵轴的分界线,从而将平面坐标系划分为六个象限(见图1)。
象限Ⅰ对应的是“高收入未脱钩”状态。此时人均GDP超过门槛值y*,且脱钩弹性系数大于0.8,即e≥0.8;y≥y*。其特点是经济增长的速度较快、规模较大,与此同时,工业污染排放的数量也急剧上升,城市经济增长与污染排放尚未脱钩。因此,象限Ⅰ代表了低效扩张的城市发展类型,也可以将象限Ⅰ视为脱钩发展滞后于经济发展的城市发展类型。对于这类城市而言,其首要任务是提高绿色技术进步,争取扭转尚未脱钩的不利局面,并努力朝着相对脱钩和绝对脱钩的方向转变。
象限Ⅱ属于“低收入未脱钩”状态。此种状态下的人均GDP没有超过门槛值y*,且脱钩弹性系数仍然大于0.8,在坐标系中表现为e≥0.8;0 象限Ⅲ描述的是“低收入相对脱钩”状态。这种发展较为缓慢且相对脱钩状态的特点是0≤e<0.8,且0 象限Ⅳ处于“高收入相对脱钩”状态。城市在这一状态下,人均GDP水平跨过门槛值y*,同时,脱钩弹性系数值处在0到0.8之间,即y≥y*,0≤e<0.8,也即城市的经济发展水平较高,并且环境污染程度趋于改善。因此,象限Ⅳ代表了集约扩张型城市,其主要任务是进一步降低污染排放量,在保持较快经济发展的同时,努力朝着绝对脱钩状态的方向迈进。 象限V为“低收入绝对脱钩”状态。最大特点是经济发展缓慢且污染排放少,对应于坐标系上e<0且0 象限Ⅳ为“高收入绝对脱钩”状态,属于绿色脱钩城市的发展类型。这一区域的脱钩弹性系数小于0,同时人均GDP水平大于门槛值y*,即e<0;y≥y*。若能在保持经济较快发展的同时,减少污染的排放,方可达到经济效益与环境效益的“双赢”。这正是象限Ⅵ所代表的绿色脱钩城市发展的理想状态:高人均收入和绝对脱钩状态的组合,既避免了单纯追求经济增长而增加环境负荷,又避免了单纯追求环境保护而降低经济发展质量。 综合上述分析可知,象限Ⅰ到象限Ⅳ分别代表了不同的城市发展类型或同一城市的不同发展阶段。那么,上述六个象限之间表现为什么样的发展规律呢?回答这一问题须厘清城市的发展到底是以经济增长为中心,还是以“绿色脱钩”为主要目标。若以经济增长为中心,那么由高到低的排序依次为象限Ⅵ>象限Ⅳ>象限Ⅰ>象限Ⅴ>象限Ⅲ>象限Ⅱ;若以“绿色脱钩”为目标,则由高到低的排序依次为象限Ⅵ>象限Ⅴ>象限Ⅳ>象限Ⅲ>象限Ⅰ>象限Ⅱ。无论哪种排序,以象限Ⅵ代表的高收入和低污染排放的组合均是最理想的状态,而以象限Ⅱ为代表的低收入和高污染排放的组合为排名末位的状态。对于一个追求经济发展,兼顾环境保护的绿色脱钩城市来说,其会经历一个由低经济发展水平低污染排放,到高经济发展水平高污染排放,再到高经济发展水平低污染排放的过程。对应到六个象限来说,绿色脱钩城市的发展轨迹由象限Ⅴ到象限Ⅲ到象限Ⅱ到象限Ⅰ再到象限Ⅳ最后到象限Ⅵ,基本呈现出一个倒“U”型曲线的发展规律。当然,象限Ⅴ到象限Ⅳ的发展并不必然要满足中间象限的逐步过渡,只要经济发展水平和脱钩状态满足必要的条件,各象限之间也可跨越式转变。 3计量分析与模型设定 3.1计量漠型与数据来源 前文关于相对脱钩与绝对脱钩的临界点正好是EKC拐点的结论,以及六个象限划分的脱钩状态均是以倒“U”型EKC假说为前提条件的。那么EKC是否表现为倒“U”型?当倒“U”型的EKC被证明存在时,脱钩弹性系数与人均GDP之间是否也存在倒“U”型曲线关系?鉴于经济增长与工业污染排放脱钩的现实意义以及数据可得性,本研究以工业SO2排放数据为例进行实证检验。 依据EKC假说,本研究将经济增长与污染排放之间非线性关系的计量模型设置为如下形式: (8) 同理,经济增长与污染排放脱钩的计量模型可以设置为以下形式: (9) 3.1.1被解释变量 式(8)中被解释变量为Pit,表示城市i第t年的工业SO2排放量(PSO2)。为保证数据的平稳性,同时消除或削减异方差问题,本研究在实证过程中对被解释变量PSO2的数据进行对数化处理lnPSO2。式(9)中的被解释变量为e。表示城市i第t年的经济增长与工业SO2排放脱钩弹性系数(eSO2),其数值依据式(1)计算而得。由于脱钩弹性系数既有正值也有负值,因此不能直接进行对数化处理。在实际检验过程中,将脱钩弹性系数(eSO2)减去样本量中的最小值(eminSO2),得到一个新的脱钩弹性系数,用ESO2表示,即ESO2=eSO2-eminSO2。由于样本量中eminSO2为负数,那么ESO2便保证了所有的脱钩弹性系数为正,且这种处理方式仅对原有数据进行平移,并不改变原来脱钩弹性系数的性质,因此对ESO2进行对数处理是有意义的,其对数形式为lnESO2。
3.1.2解释变量
yit是核心解释变量,表示城市i第t年的人均GDP水平;y2it为人均GDP的二次项,用以验证EKC假说的存在性。同理,对数化处理后的表现形式为lnpgdpit和lnpgdp2it。为剔除通货膨胀对人均GDP的影响,本研究以2004年基期,并采用人均GDP指数分别计算出2005-2013年的实际人均GDP水平。考虑到污染排放水平与脱钩状态具有很强的惯性,当年的污染排放和脱钩系数受到上年的影响,因此,本研究将取对数之后的工业S02排放量的滞后一阶(lnPSO2-i,t-1)和脱钩系数的滞后一阶(1nESO2-i,t-1)作为解释变量加入模型当中,并采用动态面板数据模型考察EKC假说和脱钩理论的性质,避免了计量模型可能出现的内生性问题,以及使用FE模型或RE模型所带来的估计偏差。
3.1.3控制变量
Xit是控制变量的集合,主要包括:工业增加值占地区生产总值的比重,表征城市的产业结构,用ind表示;实际利用外资额,衡量城市的对外开放程度,同理,对数化处理之后为lnfdi;政府的科技支出占总财政支出之比(f∞),代表技术投入对环境污染的长期影响。此外,考虑到污染排放受到环境规制的影响,本文亦将环境规制变量引入控制变量集合当中。学术界关于环境规制的衡量指标繁多,有以污染治理费用等表征的环境经济规制手段;也有以环保行政处罚案件数为代表的环境污染监管手段。本研究认为无论是经济规制还是污染监管,都只是环境规制的实施过程,并不能衡量最终的规制效果。为提高变量选取的真实性和客观性,本研究参考王杰和刘斌的做法,以工业SO2去除率(用SO2表征)代表环境规制水平,用以衡量环境规制的实际效果。
基于此,式(8)和式(9)的最终形式如下所示。
(10)
(11)
式中,ui为第i个城市的截距项;εit是误差项。
3.1.4数据来源
被解释变量脱钩弹性系数(eSO2)由工业SO2排放量和城市GDP测算得出,其中,城市GDP及GDP指数来自《中国区域经济统计年鉴》相应各期,工业SO2排放量及其去除率根据历年《中国城市统计年鉴》整理和计算得出。解释变量人均GDP及其指数来源于《中国区域经济统计年鉴》相应各期,剩下的控制变量所使用的数据,也由历年《中国城市统计年鉴》整理和计算得出。
3.2实证结果及分析
以2004-2013年中国271个地级城市的面板数据为例,并采用stata13.1软件进行实证分析。在具体检验过程中,为确保回归结果的合理性,本研究对面板数据进行了一阶差分GMM估计。在对工业SO2排放的EKC模型与脱钩模型进行AR检验时,发现上述两个模型均存在一阶差分自相关但不存在二阶差分自相关,并且Sargan检验的p值均超过了0.1,因此,二者不存在工具变量的过度识别问题。综合AR检验和Sargan检验的结果可知,EKC模型与脱钩模型的设定是合理的。上述两个模型的一阶差分GMM估计结果如表2所示。
表2显示了城市经济增长与工业S02排放之间的两条倒“U”型曲线关系的回归结果。第一条倒“U”型曲线为传统的EKC。观察EKC模型的回归结果可以发现,实际人均GDP的一次项(1npgdp)系数为正,同时二次项(lnpgdp2)系数为负,且二者均在1%的水平下显著。这表明工业S02排放量与实际人均GDP之间存在显著的倒“U”型曲线关系。根据人均GDP的一次项(1npgdp)估计参数3.311及其二次项(1npgdp2)估计参数-0.163可知,EKC拐点所对应的实际人均GDP为26 903元。我們可以将这一拐点值视为门槛值,当实际人均GDP水平尚未超过26 903元时,工业S02排放会随着人均GDP的增长而呈扩大之势,一旦跨过26 903元这一门槛值,那么工业S02排放量会随之下降。
观察表2还可发现,第二条倒“U”型曲线显示了脱钩弹性系数与人均GDP之间的非线性关联。这同样可以由实际人均GDP显著为正的一次项系数和显著为负的二次项系数得到。在上述脱钩模型中,人均GDP的一次项及其二次项的系数分别为35.434和-1.619,由此可以求出脱钩模型在拐点处所对应的实际人均GDP水平约为54 176元。同理,当实际人均GDP由54 176元的左侧向右侧迈进时,脱钩弹性系数会呈现先上升后下降的趋势,脱钩状态也会随之出现未脱钩到相对脱钩再到绝对脱钩的可能。
综上,本研究在控制了产业结构、经济开放度、科技支出以及环境规制等影响因素的条件下,通过一阶差分GMM方法考察了人均GDP与环境污染以及人均GDP与脱钩弹性系数之间的非线性关联,结果表明,一方面,城市经济增长与工业SO2排放之间倒“U”型的EKC假说得到验证;另一方面,脱钩弹性系数与人均GDP之间也呈现出倒“U”型的曲线关系。结合上文脱钩函数与EKC函数的推导结果,便得到了脱钩理论与EKC假说的内在联系,也即本研究的核心观点:经济发展与环境污染的脱钩曲线与EKC均呈倒“U”型特征,并且相对脱钩与绝对脱钩的临界点正好对应于EKC的拐点。
3.3中国271个地级城市脱钩状态的象限分布
由上述一阶差分GMM的估计结果可知,EKC拐点对应的实际人均GDP水平为26 903元。据此,可以将y*赋值为26 903元,按照y*=26 903做一条垂直于横轴的直线,再按照e=0.8做一条垂直于纵轴的直线,确立平面直角坐标系的六个象限。然后,将2004-2013年各地级城市经济增长与工业SO2排放脱钩的弹性系数均值和实际人均GDP均值作为样本量,对上述城市的脱钩状态进行象限划分。表3展示了中国271个地级城市所在象限的分布情况。
观察表3可知,在经济增长与工业SO2排放的脱钩状态中,位于象限I的城市仅有18个,在六个象限中最少,且绝大多数来自东部地区,这其中包含11个东部地区的非省会城市、4个省会城市和3个中西部城市。这类城市的特点是人均收入水平较高,但较快的经济增长伴随着很高的污染排放,以至于出现未脱钩局面。因此,象限I属于脱钩状态滞后于经济增长的城市发展类型。这类城市在今后的建设过程中,应当努力提高经济发展的资源利用率和污染排放达标率,力争做到绿色发展。
处在象限Ⅱ的城市有58个,除12个东部城市外,剩下46个城市均来自中西部(占比近80%)。这类城市大多处于经济发展水平不高,但污染排放畸高的阶段,因而属于粗放扩张的城市发展类型。由此可以看出,处于象限Ⅱ中的城市既无雄厚的经济发展基础,也不存在经济增长与污染排放的脱钩效率优势。欲达到绿色脱钩城市的建设目标,这类城市将长期面临着“保增长”和“促脱钩”的双重任务。
位于象限Ⅲ的城市最多,高达72个,其中,来自中部的城市高达45个,约占63%,且大多数是致力于发展经济的三线和四线城市。因此,以中部地区居多的象限Ⅲ中的城市属于低效扩张的发展类型。目前,我国大多数城市正处于象限Ⅲ的状态之中,尽管达到了经济增长与污染排放的相对脱钩状态,但这类城市的经济发展水平不但亟待提高,而且需要避免一味追求经济效益而增加当地环境负荷的破坏性发展。
落在象限Ⅳ的城市有37个,这其中大多是具有优越地理区位的东部沿海城市或港口城市(如大连、苏州、中山等)、较高自然资源禀赋的资源型城市(如攀枝花、马鞍山、唐山等),以及省会城市。分析可知,这类城市往往具有较高的经济发展水平,并且经济增长与污染排放之间呈现出相对脱钩的状态。因此,可以将象限Ⅳ视为集约发展的城市类型。若能在保持较快经济发展的同时,努力促进相对脱钩向绝对脱钩的发展,那么这类城市离建设绿色脱钩城市的目标就不远了。
象限Ⅴ的城市数目有54个,广泛分布于东中西部地区,既有以贵阳、南宁、西安和重庆等为代表的西部省会城市和直辖市,也有以淮南和盐城为代表的资源型城市和港口城市,还有诸如茂名、三亚、连云港等的东部城市。由于上述城市的实际人均GDP水平小于门槛值(26 903元),但经济增长与污染排放却处于绝对脱钩状态,因此,我们可以将象限Ⅴ的城市视为经济增长滞后于脱钩状态的发展类型。对于这类城市而言,其首要任务是在生态承载力可承受的范围内,以经济建设为中心,努力提高城市的人均收入水平。
象限Ⅵ拥有32个较高经济发展水平,同时达到绝对脱钩状态的地级城市。这其中大多是出自于东部地区的省会城市和沿海城市。具体来看,除10个省会城市和4个中西部城市外,剩余18个城市均来自东部地区。这类城市基本属于底子好、发展快,且产业结构以服务业为主的大城市,如北京、广州、深圳等;同时也有较高自然资源禀赋的城市,如东营、大庆、鄂尔多斯、铜陵等。以象限Ⅵ为代表的城市达到了经济发展与绝对脱钩的双重目标,可以看作是现阶段的绿色脱钩城市。
综合来看,偏重于较高人均收入水平的象限Ⅰ、象限Ⅳ和象限Ⅴ的城市数量较少,仅有87个;大多数城市分布在较低人均收入水平的象限Ⅰ、象限Ⅲ和象限Ⅴ当中,数据显示这一部分的城市数量高达1 84个,占到所有地级城市的68%。从脱钩状态来看,处于相对脱钩状态的城市最多,达到109个;绝对脱钩的城市次之,为86个;尚未脱钩的城市数量最少,仅为76个。分析这一结果可知,现阶段我国大多数城市属于经济发展水平不高,同时经济增长与污染排放处于相对脱钩状态的低效扩张类型。从象限所包含的城市分布来看,同一象限既包括相对发达的东部城市,也有不少中西部城市(比如象限Ⅱ和象限Ⅴ,这种包罗东、中、西三区域城市的情况更为突出),表明中国的城市发展存在区域内以及区域间的不均衡状态,东部地区有绿色脱钩发展相对滞后的城市,而中西部地区也有绿色脱钩发展较好的城市。尽管全国地级城市的经济增长与污染排放大多处于相对脱钩和绝对脱钩状态,但真正处于“高收入绝对脱钩”的象限Ⅵ中的城市却不到12%。这说明,目前我国城市在建设过程中不仅存在经济发展的地区不平衡,而且存在经济发展与脱钩发展不匹配的现象。打破城市经济发展滞后于脱钩发展,或者脱钩发展滞后于经济发展的状态,建设绿色脱钩城市,既面临促进尚未脱钩向相对脱钩和绝对脱钩转变,也面临进一步提升经济发展水平的双重任务。
4研究结论与政策建议
本研究首先通过数理模型的推导,综合考察了EKC假说和脱钩理论的内在联系,然后结合二者的关联,将人均GDP水平加入脱钩的判定标准,并对城市的“经济发展一环境污染”进行了脱钩的象限划分,最后将理论部分所做的推导以及脱钩的象限划分应用于实际的城市脱钩研究案例中,并依据一阶差分GMM的回归结果,将中国271个地级城市的经济发展与污染排放的脱钩状态进行了归类。
理论与实证的分析表明,EKC假说与脱钩理论满足如下三层关系:其一,经济增长与污染排放的脱钩曲线与EKC的形状一致,均呈现出倒“U”型曲线特征。其二,相对脱钩与绝对脱钩的临界点正好对应于EKC的拐点。当实际人均GDP在(-α2/6α1,-α2/2α1)的區间上时,经济增长与污染排放有可能达到相对脱钩状态;而当实际人均GDP跨过EKC的拐点-α2/2α1,并且保证连续两年的人均GDP在-α2/α1的水平之上时,城市经济增长与污染排放的绝对脱钩成为可能。根据一阶差分GMM估计结果可知,EKC拐点处对应的实际人均GDP为26 903元,这意味着,理论上中国城市的相对脱钩与绝对脱钩的临界点位于26 903元的水平。其三,结合Tapio脱钩弹性系数的划分标准和EKC拐点处对应的人均GDP水平,可以将由这二者组成的平面坐标系划分成六个象限,每一象限对应一种城市的发展类型。对2004-2013年中国271个地级城市的经验分析表明,象限Ⅰ为“高收入未脱钩”的组合,这类城市属于脱钩发展滞后于经济发展的类型。但是处于象限Ⅰ的城市较少,大多数城市广泛集中于“低收入未脱钩”的象限Ⅱ、“低收入相对脱钩”的象限Ⅲ和“低收入绝对脱钩”的象限Ⅴ当中。象限Ⅳ与象限Ⅲ类似,均达到相对脱钩状态,不同点在于落在象限Ⅳ中的城市具有更高的人均GDP水平。最后,象限Ⅵ对应于“高收入绝对脱钩”组合,是绿色脱钩城市发展的最理想状态。然而,目前中国能满足象限Ⅵ所代表的绿色脱钩城市只有32个,大部分地级城市的人均GDP水平尚未超过26 903元的门槛值,并且多数集中分布于低效扩张类型的象限Ⅲ当中。
结合EKC假说与脱钩理论的内在关联所做的象限划分,以及由此对中国271个地级城市的脱钩状态的归类可知,经济发展水平的地区不平衡,以及脱钩发展与经济发展的不匹配,制约了绿色脱钩城市的建设。因此,中国城市发展中的一个重要目标是促进尚未脱钩向相对脱钩和绝对脱钩转变,在助推脱钩状态下促进经济发展。对此,各城市发展中,要准确把握当前所处的发展形态,找准朝着哪一形态转变的发展方向。如,对于身处“低收入未脱钩”状态的城市而言,既要夯实经济基础,又要降低污染排放。再如,对于“高收入未脱钩”状态的城市来说,节能减排是其的首要任务,同时,这类城市须以提高经济发展质量为目标,通过提高绿色技术降低污染排放,最终达到绿色发展。又如,针对“低收入已脱钩”状态的城市而言,应找寻其呈现这一发展态势的特殊成因,结合自身特殊条件和生态承载力水平,完全维持脱钩状态并不现实,可在适当进入相对脱钩状态下,努力提高经济发展的速度和规模,弥补经济发展滞后于脱钩发展的缺陷。总之,绿色脱钩城市的发展,既不能单纯追求经济增长而超承载力地增加环境负荷,也不能对脱钩状态与发展水平并不匹配的局面视而不见,而应该根据城市自身的特点,选择经济增长与污染排放脱钩发展的合理目标。
(编辑:李琪)