Soliton Trains Induced by Adaptive Shaping with Periodic Traps in Four-Level Ultracold Atom Systems

M.L.Djouom Tchenkoue,D.Welakuh Mbangheku,and Alain M.Dikand´e

Laboratory of Research on Advanced Materials and Nonlinear Sciences,Department of Physics,Faculty of Science,University of Buea P.O.Box 63,Buea Cameroon

1 Introduction

The response of dielectric media to a resonant interaction with relatively intense optical fields can result into fascinating manifestations of nonlinearity.Among these the production of optical solitons[1−2]has been one of most recently considered aspects,solitons are localized structures that occur as the result of the balance of wave dispersion by nonlinearity in the medium and hence can propagate undistorted over long distances.Solitons have been demonstrated to exist in many branches of optics as for instance in optical fiber and photonic bandgap media(optical wave solitons[3]),in Bose–Einstein condensates of atomic vapors(matter wave solitons[4−7]),they also show up as light bullets in periodic arrays of optical waveguides,[8]localized ring vortex pulses in thermooptical media,[9]trapped photon states in the waveguide of a Kerr optical medium,[10−11]and so forth.

Adaptive optics,one of the new-born fields of nonlinear optics,offers a number of interesting possibilities to use light to control light.[12]For instance,an optical lattice can be used to trap,reshape and convey light in nonlinear media in forms of optical solitons.[11]Among the current issues in this later field the manipulation of ultracold atoms by strong optical fields,has become a particularly attractive topic.Of most interest is the phenomenon of Electromagnetically-Induced Transparency(EIT),[13−14]a quantum interference process that enables the propagation of light without attenuation in an opaque medium.Because the EIT manifests itself through a narrow windows of transparency within the absorption pro file,and most importantly can involve a step positive dispersion with induced nonlinearity in the refractive index of the medium,optical solitons are indeed most likely to form and have been observed in ultracold three-state and fourstate atom systems.[15−20]In these systems optical solitons originate from intense electromagnetic radiations related to the detuning of the excitation beams from resonance,which induces a Kerr nonlinearity in the atomic system.[21]However,in some applications,there is a desire to keep full control[12,22−24]on shape pro files and propagation characteristics of these optical solitons.This can require an optical trap from another field,also interacting with the system.In this respect periodic fields have been among some of the optical traps considered in the recent literature(see e.g.Refs.[25–26]).These specific optical traps create a periodic grating leading to an optical waveguide[27−28]along the path of the travelling elecromagnetic field.Such a periodic optical waveguide can,for instance,be formed by the interference of counterpropagating intense lasers that imprint periodic grating in the dielectric medium.EIT has been achieved in different types of solid-state materials such as Pr3+doped Y2SiO5,[29−30]and semiconductors.[31]

In this work,we address the issue of a possible generation of soliton trains in optical media experiencing the phenomenon of EIT.In this goal,we consider a four-level ultracold atom system embedded in a planar dielectric medium,interacting with three different optical fields one of which creates an optical trap vis-`a-vis a probe.[25]Two different optical traps will be considered,both represented by a lattice of spatially entangled optical solitons forming a periodic grating along the path of the probe field.Our aim is to show that the competition between the self-phase modulation created by the EIT phenomenon on one hand,and the cross-phase modulation related to the soliton-lattice waveguiding structure,on the other hand,can give rise to an exceptionally rich spectrum of stationary nonlinear structures.In particular this specific type of optical traps can promote soliton-crystal fields[32−33]in the system as predicted[34]and observed in self-induced transparency systems.[35−36]

2 The Model and Nonlinear Propagation Equation

Consider a four-level ultracold atom system embedded in a dielectric medium such as a photonic crystal(Fig.1(a)),which interacts simultaneously with three different laser fields(Fig.1(b)):The ground states|1〉and|2〉,with energiesE1= ħω1andE2= ħω2respectively,are excited to a common state|3〉of energyE3= ħω3,by a weak probe fieldEpof a Rabi frequency Ωp=℘31Ep/ħ and a strong coupling fieldEcwith a Rabi coupling frequency Ωc=℘32Ec/ħ.The fieldsEpandEcare detuned from resonance with respective detuning Δ1and Δc.In order to generate an optical lattice a third field,which we shall refer to as induction field,couples the|2〉↔ |4〉transition with a Rabi frequency ΩI=℘42EI/ħ and detuning Δ2from resonance.This con figuration is a simple example of an N-type four-levelultracold atom system(see e.g.Ref.[25])driven by three fields,where the states|1〉,|2〉,|3〉form a three-level Λ-type EIT scheme with all atoms assumed to be intially in the lowest state|1〉.At two-photon resonance(δ= Δ1−Δc=0),the probe absorption will be annihilated by the intense driving field inducing transparency of the medium.[25]If we assumeΩc≫ (Ωp,ΩI),the actions of Ωpand ΩIcan readily be looked out as perturbation in the system.Therefore,in the interaction picture,the total Hamiltonian of the system can be writtenˆH=ˆH0+ˆH1where:

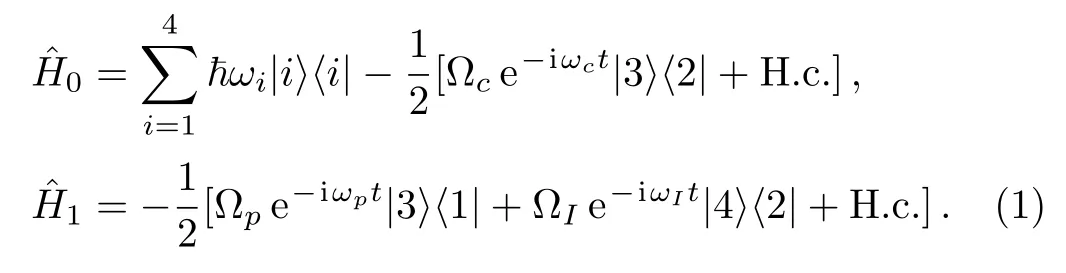
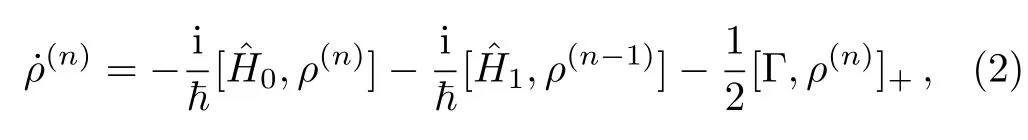
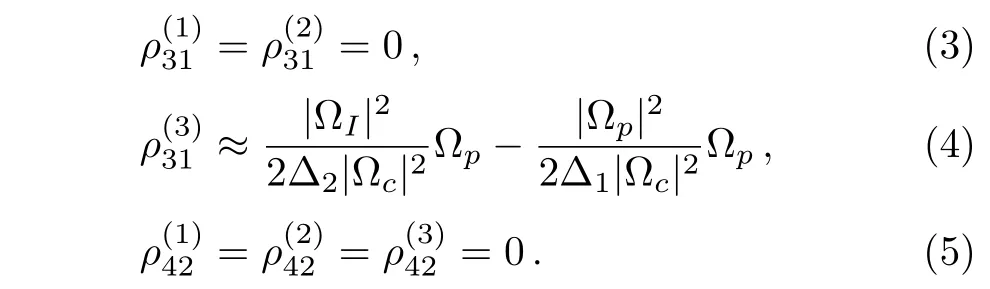
To describe the propagation of the probe field,we consider a quasi-one-dimensional dielectric medium and assume that the field propagates along thexaxis,while undergoing weak modulations along the transverse propagation axisz.In the paraxial approximation such a quasione-dimensional,transverse-modulated wave is governed by the wave equation(so-called paraxial wave equation):

wherePp=2N℘31ρ31is the polarization andkpthe wavector of the probeEp.Nis the number of atoms,Equation(6)suggests that the polarization of the probe fieldEpis proportional to the intensities of the induction fieldEIand of the probe field itselfEp.The first of these two contributions corresponds actually to a crossphase modulation process created by the induction field,while the second contribution is a self-phase modulation term representing a giant Kerr nonlinearity generated by EIT.[21]These two important contributions to the nonlinear modulations of the fields propagating in the dielectric medium,appear more explicitely by replacing(4)inPpand thenPpin Eq.(6).Finally,by settingΩP(X,z)=℘31Ep(X,z)/ħ=A(X)exp(−ikzz),wherekzis the transverse modulation wavector,we find:

withX=xkp,β=2kz/kp,and where the potentialV(X)and the nonlinear coefficientκhave been defined respectively:

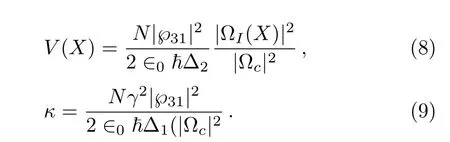
As it is apparent,the optical potentialV(X)induced by the field ΩIdepends on sign of the detuning Δ2(remarking the detuning can be above or below resonance).It turns out that when Δ2＜0,the potential is a focusing optical trap whereas for a positive detuning i.e.Δ2＞0,the potential is a defocusing optical trap.Similarly,the detuning Δ1in the expression ofκsuggests the possibility of a self-focusing(Δ1＜0)or self-defocusing(Δ1＞0)of the propagating field,due to self-phase modulation.In the next section we show that the account of the signs of the detuning give rise to a rich spectrum of optical-soliton fields generated by means of EIT in the dielectric medium.

Fig.1 (a)A system of ultracold atoms driven by three fields.(b)The energy scheme of the N-type atom system showing the transitions.Δ1,Δ2,Δcare the detuning of the respective electric fields.

3 Soliton-Train Spectra

Equation(7)describes the nonlinear spatial modulation of the probe field in an optical trapV(X),created by a control field co-propagating with the probe.The same equation was derived recently in a similar context,but considering a control field from a continuous source i.e.of the formV(X)∝sin2(X).[25]For this later case,when the self-phase modulation term is absent the probe field obeys a linear eigenvalue problem with a square sinusoidal potential whose solutions are Floquet–Bloch modes.[37−38]On the other hand,when the square sinusoidal potential competes with the self-phase modulation nonlinearity,the soliton solutions generated via the Kerr nonlinearity are unstable nonlinear periodic structures since the sinusoidal potential will tend to create oscillations in the soliton wings,whose amplitudes grow with the strength of the potential.[25]In this work we will instead deal with a relatively more intense optical trap with a periodic but non sinusoidal pro file,in particular we consider two distinct forms of such optical traps made up of pulse-shaped and tanh-shaped intensity fields respectively,spatially multiplexed to form a robust nonlinear periodic grating in which the probe field remains always trapped.The two periodic traps,which have also been used in the context of Bose–Einstein condensates[39−40]to study the simultaneous localization and confinement of matter-wave solitons in periodic nonlinear traps,are given by:

(i)Nonlinear periodic trap with sharp bottoms and flat tops:[40]

(ii) Nonlinear periodic trap with flat bottoms and sharp tops:[39]

In these two formula sn and cn are Jacobi elliptic functions of modulusν(0≤ν≤1),their shape pro files are plotted in Fig.2 for positive and negative values of their amplitudesV0(accounting for the cases of a negative or a positive deturning Δ2),and forν=0.98.Whenν→0,the Jacobi elliptic functions sn(X)→sin(X)and cn(X)→cos(X)respectively,which are the particular cases treated in Ref.[25].On the other hand,whenν→1,the Jacobi elliptic functions sn(X)→tanh(X)and cn(X)→sech(X)respectively,leading to the other extreme regime where the optical trap is a single-pulse soliton field.It should be noted that whenνis neither equal to zero nor equal to one,the elliptic function

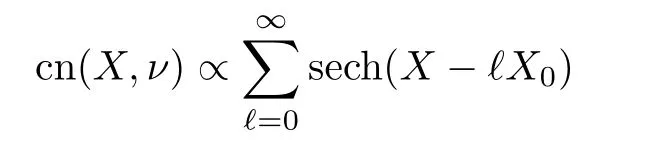
and sn(X,ν)

Fig.2 Periodic optical traps generated by the induction field:(a)the “sn2” potential given by formula(10),(b)“cn2” potential given by formula(11).In the two graphs the upper curve corresponds to positive V0(“expulsive”optical trap),and the lower curve to negative V0(“attractive” optical trap).

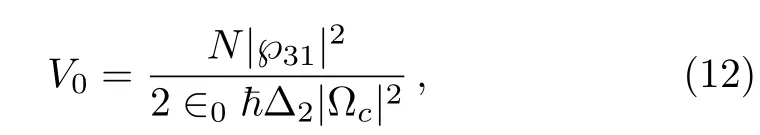
the sign of which is fixed by the sign of the detuning Δ2as already mentioned.

As we are interested in stationary solutions to Eq.(7),the functionA(X)should be real.Also relevant to stress,

For mathematical simplifications,in formula(8)we take ΩI(X)=sn(X,m)and ΩI(X)=cn(X,m)such that the two potentials have the same amplitude:we want the periodic trap to control shape pro files of the stationary field.To this end we first solve the Lam´e-type“eigenvalue problem” in Eq.(7)without the nonlinear term following the standard method,[41]and then use the self-phase modulation term to evaluate the amplitudes of the different eigen-modes of the Lam´e equation.

In Tables 1 and 2,we list all the six allowed solutions corresponding to the two periodic optical traps(10)and(11)respectively,together with their corresponding transverse modulation wavectorkz.

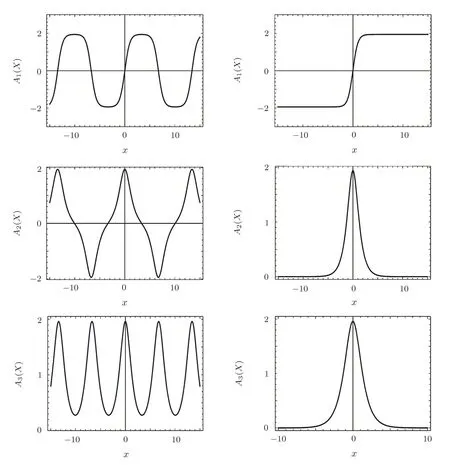
Fig.3 Wave pro files of the three periodic-soliton solutions Aj(j=1,2,3)listed in Tables 1 and 2,for ν=0.98(left column)and ν=1(right column).

The following relevant remarks ensue from solutions listed in the two tables:

The two types of optical traps lead to the same soliton modes,except their “quantum numbers”kzwhich will be different.

The second remark concerns the stability of the optical solitons resulting from the competition between the self-phase modulation of strengthκ,and the cross-phase modulation of strengthV0.Indeed,for the first optical trap(i.e the “sn2”potential),results of Table 1 suggest that the stationary modesA1(X),A4(X)andA5(X)are always stable when the two detunings Δ1and Δ2are positive,or when they are both negative but with a judicious choice of values of the modulusνof the Jacobi elliptic functions.When the two detunings are of opposite signs(that is,the control field is detuned above resonance and the probe is detuned below resonance or vice-versa),the stability of these three solutions requires appropriate choices of the cross-phase modulation strengthV0and the self-phase modulation strengthκ,with respect toν.For instance,ifV0is negative(confining optical trap)and the self-phase coefficientκis positive(self-focusing selfphase modulation),the magnitude|V0|of the cross-phase term will be smaller than one so that contribution from the self-phase modulation phenomenon will dominate the nonlinear feature of the periodic optical solitons.On the contrary,ifκis negative(self-defocusing self-phase modulation)and the optical trap is an expulsive field,the three solutions will be always unstable.

As for the stability of solutions listed in Table 2,corresponding to the second optical trap(i.e.the “cn2” potential),an analysis similar to the previous case suggests that when Δ1is positive and Δ2is negative,the three solutionsA1(X),A4(X),andA5(X)are always stable.They are always unstable if the two detunings are positive with a relatively strong cross-phase modulation.When the selfphase modulation produces a self-focusing effect on the probe,the cross-phase modulation must be a strong expulsive field to ensure stability of the three optical solitons.More generally,stability criteria of all the optical soliton modes listed in the two tables can be established by a simple analysis of the quantities in the square root,corresponding to their amplitudes.

Fig.4 Wave pro files of the three periodic-soliton solutions Aj(j=4,5,6)listed in Tables 1 and 2,for ν=0.98(left column)and ν=1(right column).

Another relevant point to consider in the analysis of solutions listed in Tables 1 and 2,is their spatial pro files.Since the two different optical traps considered lead to analytically similar solutions,in Fig.3 we sketched only the three first solutions i.e.A1(X),A2(X),while in Fig.4 we sketched the three last solutions i.e.A4(X),A5(X)andA6(X).The left graphs in the two figures represent spatial pro files of the solutions forν=0.98,while the right graphs are spatial pro files of their corresponding one-soliton constituent(i.e.forν=1).Remarkably,A6(X)is unstable whenν=1.

Table 1 Stationary solitons for V1(X)=V0sn2(X,ν).

Table 2 Stationary solitons for V2(X)=V0cn2(X,ν).

A comparision of periodic structures in the left graphs of Figs.3 and 4,with their one-soliton(i.e.hyperbolicfunction solutions)limits in the right,suggests the following information about the natures of their fundamental components:

•A1(X)is a periodic lattice of kink solitons,

•A2(X)andA3(X)are periodic lattices of pulse solitons,

•A4(X)andA5(X)are periodic lattices of brightdark solitons,

•A6(X)admits no one-soliton limit and can therefore only exist as a periodic-soliton structure.

Analytically,the one-soliton limits of the six periodicsoliton modes are expressed as follows in terms of hyperbolic functions:

The values ofkzassociated to these one-soliton modes,are derived from formula in Tables 1 and 2 forν=1.

4 Conclusion

We investigated the spatial pro files of a probe field propagating in a four-level ultracold atom system,embedded within a dielectric medium with a Kerr nonlinearity generated by electromagnetically-induced transparency.The problem was formulated in terms of a stationary field,whose spatial pro file is determined by a periodic nonlinear optical trap but the amplitudes by the competition between the Kerr-type self-phase modulation nonlinearity and the periodic optical trap.The governing equation has been solved following a method that allows generating the solutions as a sprectrum of soliton-train modes with distinct quantum numbers,here represented by the transverse modulation wavector,in contrast with the singlesoliton mode found for the same equation in previous works in the context of Bose–Einstein condensates.[39−40]

It is interesting to stress that the solutions found in our study suggest the possibility to convert a pulse-soliton into a dark-soliton field and even dark-bright soliton mode,by propagating a pulse or a dark soliton train in an appropriate optical soliton-induced waveguide structure.To this last point,when there is no optical trap,the spatial pro file of the probe envelope obeying the nonlinear Schrödinger equation(6)will be determined solely by the sign of the nonlinear coefficientκ.However,the solutions listed in the two tables above clearly show that the competition between the optical trap and the self-phase modulation favors the emergence of complex and unexpected structures which would be either unstable,or impossible to form in the medium without being reshaped in the periodicgrating structure created by intense optical fields.EIT phenomena have been predicted to occur in atomic vapors and beams,[18,42]in solid state materials such as Pr3+doped Y2SiO5,[29]diamond,[43]semiconductors[31]and so on.The novel periodic soliton structures proposed in the present study should also play a significant role in all these physical systems.

Acknowledgments

The Laboratory of Research on Advanced Materials and Nonlinear Science(LaRAMaNS),is supported in part by the Academy of Science for the Developing World(TWAS).

References

[1]H.A.Haus and W.S.Wong,Rev.Mod.Phys.68(1996)423.

[2]S.Yu Kivshar and B.Luther-Davies,Phys.Rep.298(1998)81.

[3]G.P.Agrawal,Nonlinear Fiber Optics,3rd ed.Academic,New York(2001).

[4]B.Wu,J.Liu,and Q.Niu,Phys.Rev.Lett.88(2002)034101.

[5]Th Bush and J.R.Anglin,Phys.Rev.Lett.87(2001)010401.

[6]S.Pötting,M.Cramer,and P.Meystre,Phys.Rev.A 64(2001)063613.

[7]A.M.Dikand´e,J.Math.Phys.49(2008)073620.

[8]S.Minardi,et al.,Phys.Rev.Lett.105(2010)263901.

[9]A.M.Dikand´e,Europhys.Lett.94(2011)44004.

[10]K.Steiglitz and D.Rand,Phys.Rev.A 79(2009)021802.

[11]A.M.Dikand´e,Phys.Rev.A 81(2010)013821.

[12]F.Kajzar and R.Reinisch,Beam Shaping and Control with Nonlinear Optics,(eds.),NATO ASI Series B 369(2002).

[13]A.Imamoglu and S.E.Harris,Opt.Lett.14(1989)1344.

[14]M.D.Lukin and A.Imamoglu,Nature(London)413(2001)273.

[15]G.Huang,L.Deng,and M.G.Payne,Phys.Rev.E 72(2005)016617.

[16]G.Huang,K.Jiang,M.G.Payne,and L.Deng,Phys.Rev.E 73(2006)056606.

[17]Z.Chen,Z.Bai,and G.Huang,Scientific Reports.5(2014)8211.

[18]K.J.Boller,A.Imamoglu,and S.E.Harris,Phys.Rev.Lett.66(1991)2593.

[19]D.Wei,J.F.Chen,M.M.T.Loy,K.G.L.Wong,and S.Du,Phys.Rev.Lett.103(2009)093602.

[20]D.A.Braje,V.Balic,S.Goda,G.Y.Yin,and S.E.Harris,Phys.Rev.Lett.93(2004)183601.

[21]H.Wang,D.Goorskey,and M.Xiao,Phys.Rev.Lett.87(2001)073601.

[22]G.Vemuri,D.S.Agarwal,and K.V.Vasavada,Phys.Rev.Lett.79(1997)3889.

[23]C.Hang,V.V.Konotop,and G.Huang,Phys.Rev.A 79(2009)033826.

[24]Y.Qi,Y.Niu,Y.Xiang,S.Jin,and S.Gong,Phys.Rev.E 82(2010)016602.

[25]W.Pang,J.Wu,Z.Yuan,Y.Liu,and G.Chen,J.Phys.Soc.Jpn.80(2011)113401.

[26]C.Hang and V.V.Konotop,Phys.Rev.A 81(2010)053849.

[27]S.Flach,V.Fleurov,A.V.Gorbach,and A.E.Miroshnichenko,Phys.Rev.Lett.95(2005)023901.

[28]D.Palima,A.R.Ba˜nas,G.Vizsnyiczai,L.Kelemen,P.Ormos,and J.Glückstad,Opt.Express.20(2012)2004.

[29]A.V.Turukhin,V.S.Sudarshanam,M.S.Shahriar,J.A.Musser,B.S.Ham,and P.R.Hemmer,Phys.Rev.Lett.88(2002)023602.

[30]J.J.Longdell,E.Fraval,M.J.Sellars,and N.B.Manson,Phys.Rev.Lett.95(2005)063601.

[31]G.B.Serapiglia,E.Paspalakis,C.Sirtori,K.L.Vodopyanov,and C.C.Phillips,Phys.Rev.Lett.84(2000)1019.

[32]D.Jr Fandio Jubgang,A.M.Dikand´e,and A.Sunda-Meya,Phys.Rev.A 92(2015)053850.

[33]D.Jr Fandio Jubgang and A.M.Dikand´e,J.Opt.Soc.Am.B 34(2017)2721.

[34]A.M.Kamchatnov and M.V.Pavlov,JETP Lett.80(1995)22.

[35]S.L.McCall and E.L.Hahn,Phys.Rev.183(1969)457.

[36]A.I.Maimistov,A.M.Basharov,S.Elyutin,and Yu M.Sklyarov,Phys.Rep.191(1990)1.

[37]M.Horne,I.Jex,and A.Zeilinger,Phys.Rev.A 59(1999)2190.

[38]J.T.Cole and A.T.Musslimani,Phys.Rev.A 90(2014)013815.

[39]R.Carretero-Gonzalez and K.Promislow,Phys.Rev.A 66(2002)033610.

[40]J.C.Bronski,L.D.Carr,R.Carretero-Gonz´alez,N.Deconinck,J.N.Kutz,and K.Promislow,Phys.Rev.E 64(2001)056615.

[41]A.M.Dikand´e,J.Opt.13(2011)035203.

[42]H.R.Gray,R.M.Whitley,and Jr C.R.Sdtroud,Opt.Lett.3(1978)218.

[43]C.Wei and N.B.Manson,Phys.Rev.A 60(1999)2540.