Exhibition of Monogamy Relations between Entropic Non-contextuality Inequalities∗

Feng Zhu(朱锋),Wei Zhang(张巍), and Yi-Dong Huang(黄翊东)

Tsinghua National Laboratory for Information Science and Technology,Department of Electronic Engineering,Tsinghua University,Beijing 100084,China

The quantum theory shows the property of contextuality,which conflicts with the noncontextual hidden variable(NCHV)theory.[1]The non-contextuality inequalities are derived from the noncontextual hidden variable theory,such as the KCBS inequality[2]and state-independent contextuality inequalities.[3]The quantum bounds of these non-contextuality inequalities are different from the noncontextual hidden variable bounds.The local hidden variable theory is a special type of noncontextual hidden variable theory.Hence,the Bell inequality such as the CHSH inequality can be also treated as a non-contextuality inequality.[4]The contextuality of quantum theory can be demonstrated by the experimental observations of the violations of the non-contextuality inequalities.[5−9]

Entropic test is a way to investigate the quantum contextuality.[10−11]The conditional entropyH(A|B)is

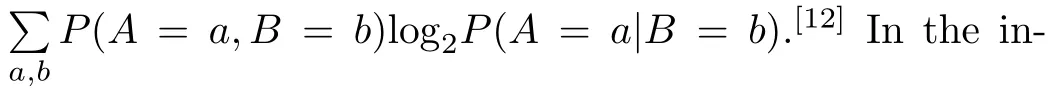
formation theory,it denotes the information to describe the outcomes of the observableAwhile the outcomes of the observableBare given.The entropic test can be utilized in investigating on the marginal problems.[13]The entropic non-contextuality inequality is formulated in the noncontextual hidden variable theory[10−11]by the chain rule.[12]A number of entropic inequalities defines the convex Shannon cone.[14]They also can distinguish different causal structures.[15]

The monogamy relation is a trade-off between the violations of two non-contextuality inequalities.[16−17]The violation of one inequality forbids the violation of the other.This relation is originated from the no-signaling principle and the no-disturbance principle.[16−17]The monogamy relations between two Bell inequalities,[16]a Bell inequality and a KCBS inequality,[18]and two KCBS inequalities,[17]have been demonstrated. It is utilized in the investigations such as the security of quantum key distribution[19]and the local realism of macroscopic correlations.[20]The monogamy relation of the entropic inequalities can be interpreted as a classical quantification of causal influence.[21]

The monogamy relation between non-contextuality inequalities can be investigated by the graph theory.[17]In Refs.[17]and[18],the monogamy relation is exhibited by decomposing the compatibility graph into chordal subgraphs.A chordal graph is a graph without any induced cycle,which has vertices more than three vertices. If the compatibility relations among observables satisfy a chordal compatibility graph,it admits a noncontextual hidden variable model.[17]It has a joint probability distribution,which recovers all joint measurable probabilities as marginal.Hence,the monogamy relation can be exhibited if the compatibility graph can be decomposed into chordal subgraphs{Gs}and∑sα(Gs)=R1+R2,whereR1andR2are the NCHV bounds of the two non-contextuality inequalities.[17]

In this Letter,we investigate the monogamy relation between two entropic non-contextuality inequalities in the scenario where compatible projectors are orthogonal.

Let us consider widely used local scenarios,in which there is a system with a set of two-value observables{A1,...,An}.The outcome of each observableAiisai,ai∈{1,−1}.Two compatible observablesAiandAjhave orthogonal projectors Πiand Πj.AiandAjcan be represented asAi=2Πi−1 andAj=2Πj−1(the rank of the projectors is arbitrary positive integer).In this scenario,the outcomes ofAiandAjcan not be 1 simultaneously.

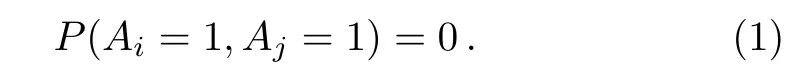
This scenario is originated from the Kochen–Specker scenario and includes most local scenario.[1−3,10−11,17,24−26]

In this scenario,any probability of a joint measurable observable setP(Aj1=aj1,...,Ajm=ajm)can be represented as a linear combination of the probabilities of single measurementP(Ajk=ajk).For example,

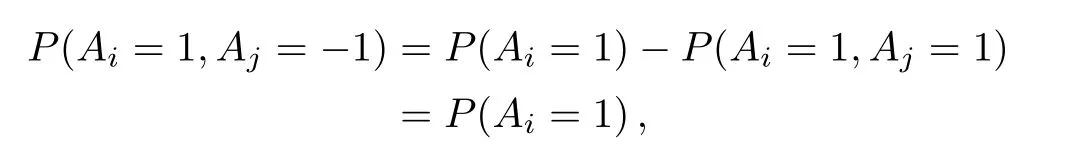
and

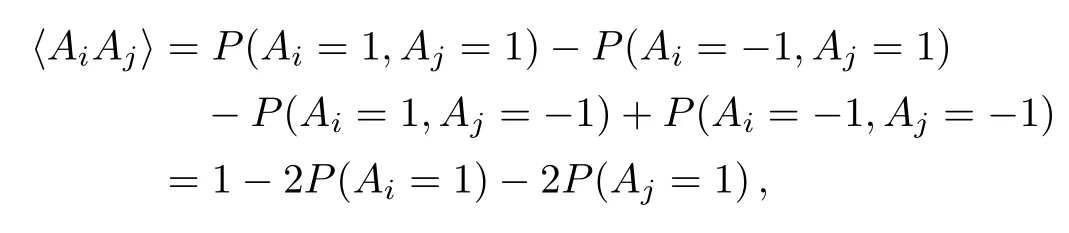
whereAiandAjare compatible.

The exclusivity graph shows the exclusive relations among the events.[24−25,30−31]The exclusivity events correspond to orthogonal projectors while compatible observables correspond to more general compatible operators.The compatibility graph shows the compatible relations among the observables.[11,17−18]To investigate the non-contextualtiy inequalities in the scenario satisfying Eq.(1),the orthogonality graph is suitable.Each vertex representsP(Ai=1)and each edge indicates the orthogonality relation between two events of vertices it links.The topological structure of the orthogonality graph in this scenario is as same as that of the compatibility graph.The exclusivity graph of an observable set is reduced to the orthogonality graph in this scenario.For example,as the equations before,the verticesP(Ai=1,Aj=−1)andP(Ai=1,Ak=−1)in the exclusivity graph are merged into one vertexP(Ai=1)in the orthogonality graph and the vertexP(Ai=1,Aj=1)of the exclusivity graph can be omitted.

From the graph theory,the noncontextual hidden variable bound of a KCBS-type non-contextuality inequalities(the non-contextuality inequality where the left part is the sum of probabilities of measurement events[17])is the independence numberα(G),[25,27]which is the vertex number of the largest independent set.[27−28]The quantum bound of a KCBS-type non-contextuality inequality is the Lov´asz numberϑ(G).[25,27]The set of the probabilities of the observables in the noncontextual hidden variable theory is the vertex packing polytope VP(G)[25,27]The set of the probabilities of the observables in the quantum mechanics is the Grötschel–Lov´asz–Schrijver set TH(G).[25,27]TH(G)=VP(G)holds if and only if the orthogonality graphGis perfect.[25,27]Hence,the quantum and the noncontextual hidden variable bound of an inequality correspond to a perfect orthogonality graph are the same in this scenario.It can be utilized to exhibit the monogamy relation.

Result 1In the scenario satisfying Eq.(1)

(i)Two KCBS-type non-contextuality inequalities can exhibit the monogamy relation if the orthogonality graph of two KCBS-type non-contextuality inequalities can be decomposed into perfect subgraphs such that the sum of independence numbers of these subgraphs is equal to the sum of the NCHV bounds of two non-contextuality inequalities.

(ii)The method in Eq.(1)is equivalent to the method in Ref.[17]which is exhibited by decomposing the orthogonality graph into chordal subgraphs while the sum of independence numbers of these subgraphs is equal to the sum of the NCHV bounds of two non-contextuality inequalities.

Proof

(i)In the scenario satisfying Eq.(1),G1andG2represent the orthogonality graphs of two KCBS-type noncontextuality inequalities.Their perfect subgraphs are denoted by{Gs}.The sum of independence numbersα(Gs)of these subgraphs is equal to the sum of the independence numbersα(G1)(α(G2))of the original orthogonality graphs.The monogamy relation can be exhibited.

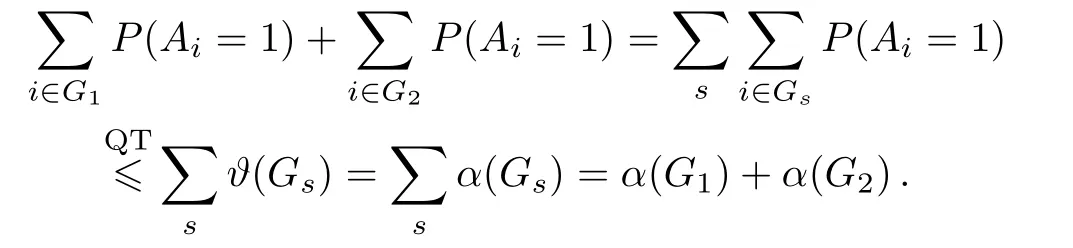
(ii)Comparing with the result in Ref.[17],we find the exhibition of monogamy relation between KCBS-type inequalities by decomposing into chordal subgraphs is equivalent to that by decomposing into perfect subgraphs.

(a)Chordal decomposition⇒Perfect decomposition.

Since the chordal graph does not have any cycle as its induced subgraph,it does not have any odd cycle or odd cycle’s complement as its induced subgraph.Hence,it is a perfect graph.[28]If the monogamy relation can be exhibited by decomposing the orthogonality graph into chordal subgraphs,this exhibition also can be treated as a result of decomposing the original orthogonality graph into perfect subgraphs.

(b)Prefect decomposition⇒Chordal decomposition.

If the monogamy relation between two KCBS-type non-contextuality inequalities can be exhibited by decomposing the corresponding orthogonality graph into perfect subgraphs{Gs},there is∑sα(Gs)=R1+R2.Since{Gs}are perfect,α(Gs)=¯χ(Gs),where¯χ(Gs)denotes the clique cover number which is the minimum number of cliques needed to cover graph.[27−28]Hence,each subgraphGscan be decomposed into cliques{Gs,t}with the number of¯χ(Gs).The sum of the noncontextual hidden variable bounds of these clique subgraphs is:

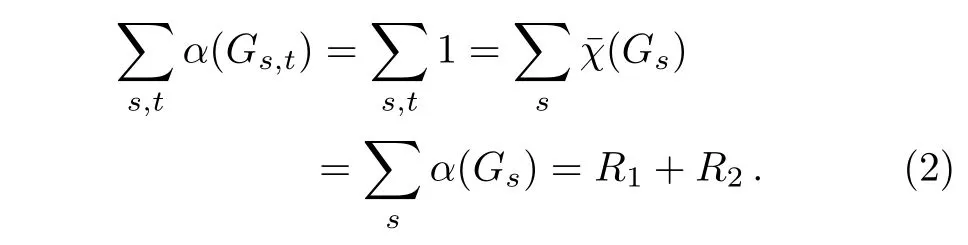
According to the equation above,the monogamy relation can be exhibited by decomposing the orthogonality graph into cliques,which are chordal. □

For the monogamy relation between entropic noncontextuality inequalities,the exhibition method is different since the inequalities are based on cycles in the orthogonality graphs.With the chain ruleH(A|C)≤H(A|B)+H(B|C),the entropic non-contextuality inequality is derived as:

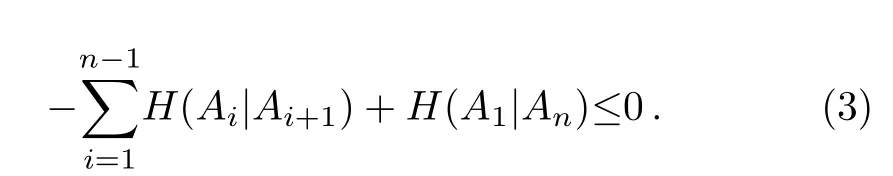
The orthogonality graph of the observable set{A1,...,An}is a cycle.Equation(3)is violated while its left part can be equal to 0.091(bit)in quantum theory whenn=5.[11]The reason is the observable set lacks the joint probability distribution.[22]

Since even cycles are perfect but odd cycles are not,in the scenario satisfying Eq.(1),the observable set correspond to orthogonality graph has the joint probability distribution. Considering the bounds of entropic noncontextuality inequalities in the noncontextual hidden variable theory are always zero,the veri fication of Eq.(2)is not required.

Result 2In the scenario satisfying Eq.(1),the orthogonality graphs of two observable sets{A1,...,An}and{,...,} (n≥5)are two odd cyclesCnwith two shared verticesA1=andAn+2−m=(2≤m≤n)as shown in Fig.1(a).

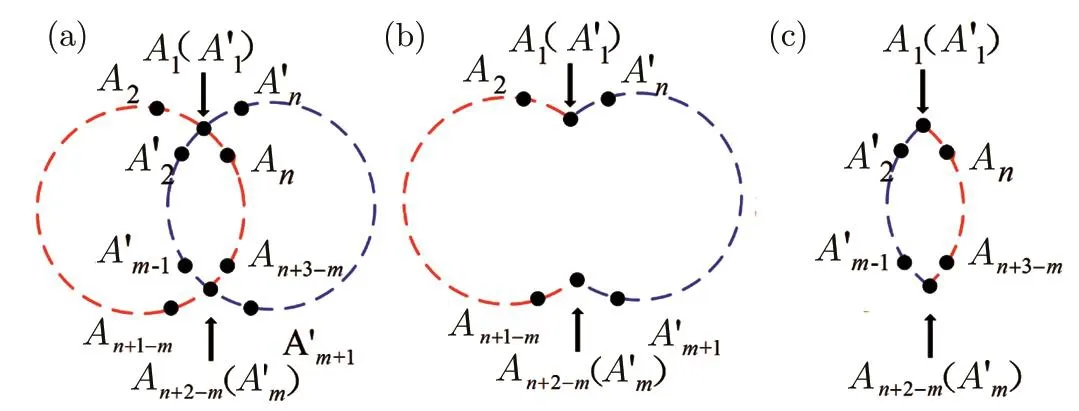
Fig.1 The orthogonality graph of two odd cycles with two shared vertexes.

(i)Two KCBS-type non-contextuality inequalities shown in Eqs.(4)are not monogamous.

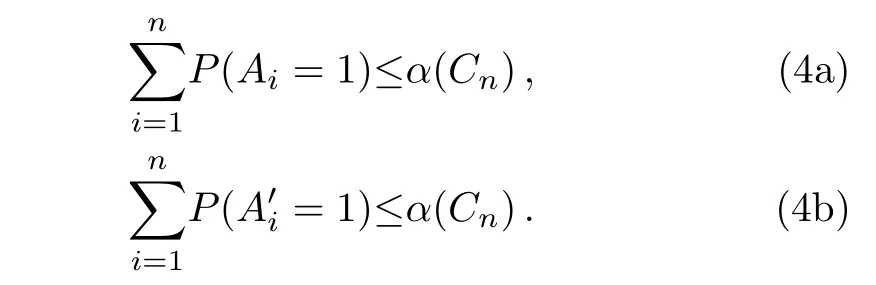
(ii)Two entropic non-contextuality inequalities shown in Eqs.(5)are monogamous.(two positive terms appear of Eqs.(5)must appear in different even cyclic induced subgraphs.)

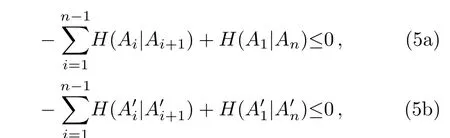
whereHdenotes the conditional entropy.

Proof

(i)There exists a state|φ〉and an observable set{A1,...,An},Ai=2|vi〉〈vi|− 1,satisfying the orthogonality graph in Fig.1 and

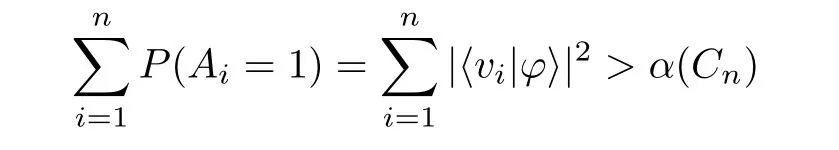
leading the violation of Eq.(4a).[28]

Since the dimension of the spaceS1spanned by{|φ〉,|v1〉,|v2〉,...,|vn〉}is finite,one can find a newn-dimensional spaceS2which is orthogonal toS1.{|u1〉,...,|un〉}are the complete orthogonal basis of the ’spaceS2.They satisfy that:

As a result,Eqs.(5)can be violated simultaneously under the state|φ〉and two observable sets{A1,...,An}and{,...,}satisfying the orthogonality graph shown in Fig.1(a).

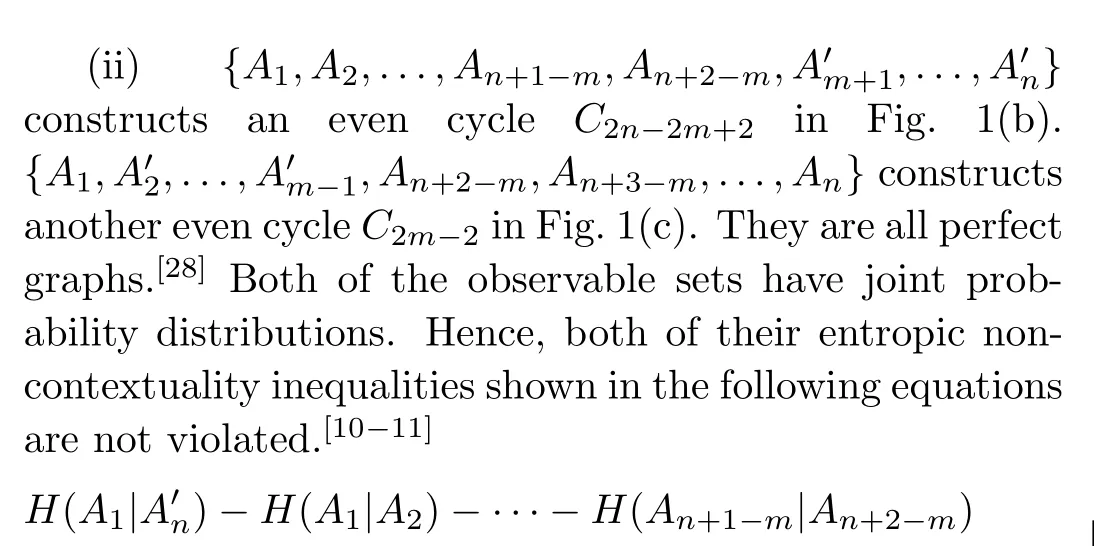
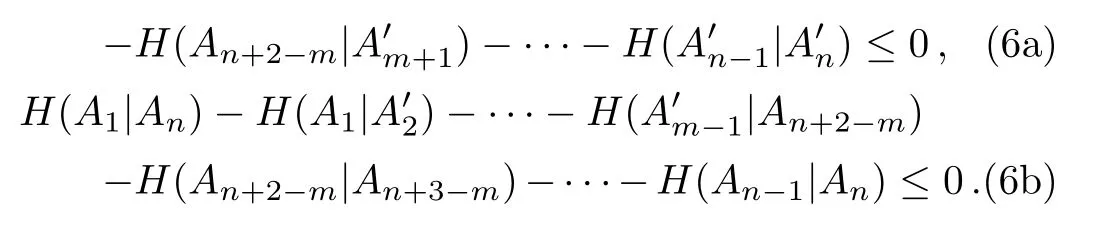
The sum of Eqs.(6)indicates the monogamy relation between Eq.(5a)and Eq.(5b). □

Here we show an example of Result 2.The state vector is|ψ〉=[1,0,0,0,0]and the observables areAi=2|vi〉〈vi|− 1,where

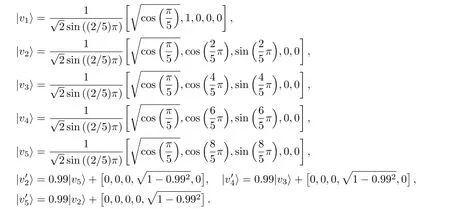
The observables satisfy the orthogonality graph of two pentagons with two shared vertices.Equations(4)are violated simultaneously while Eqs.(5)are monogamous.

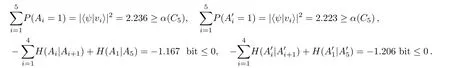
We investigate the monogamy relation between two entropic non-contextuality inequalities in the scenario satisfying Eq.(1).We show the monogamy relation can be exhibited by decomposing the orthogonality graph into perfect subgraphs.We compare two methods to exhibit the monogamy relation between two non-contextuality inequalities in this scenario,which are based on the decompositions of the corresponding orthogonality graph into perfect subgraphs and chordal subgraphs,respectively.We obtain that they are equivalent for the analysis on the KCBS-type non-contextuality inequalities.Then,we investigate the monogamy relation between two KCBS-type inequalities and entropic non-contextuality inequalities if their orthogonality graphs are two odd cycles with two shared vertices.We prove two entropic non-contextuality inequalities are monogamous while the KCBS-type noncontextuality inequalities are not.

References

[1]E.P.Specker,Dialectica 14(1960)239;S.Kochen and E.P.Specker,J.Math.Mech.17(1967)59;J.S.Bell,Rev.Mod.Phys.38(1966)447.

[2]A.A.Klyachko,M.A.Can,S.Binicio˘glu,and A.S.Shumovsky,Phys.Rev.Lett.101(2008)020403.

[3]A.Cabello,Phys.Rev.Lett.101(2008)210401;S.Yu and C.H.Oh,Phys.Rev.Lett.108(2012)030402.

[4]J.S.Bell,Physics 1(1964)195;J.F.Clauser,M.A.Horne,A.Shimony,and R.A.Holt,Phys.Rev.Lett.23(1969)880.

[5]G.Kirchmair,F.Zähringer,R.Gerritsma,et al.,Nature(London)460(2009)494.

[6]R.Lapkiewicz,P.Li,C.Schaeff,et al.,Nature(London)474(2011)490.

[7]J.Ahrens,E.Amselem,A.Cabello,and M.Bourennane,Sci.Rep.3(2013)2170.

[8]X.Zhang,M.Um,J.Zhang,et al.,Phys.Rev.Lett.110(2013)070401.

[9]E.Amselem,M.R˚admark,M.Bourennane,and A.Cabello,Phys.Rev.Lett.103(2009)160405;E.Amselem,L.E.Danielsen,A.J.L´opez-Tarrida,et al.,Phys.Rev.Lett.108(2012)200405.

[10]R.Chaves and T.Fritz,Phys.Rev.A 85(2012)032113.

[11]P.Kurzy´nski,R.Ramanathan,and D.Kaszlikowski,Phys.Rev.Lett.109(2012)020404.

[12]C.E.Shannon and W.Weaver,The Mathematical Theory of Communication,University of Illinois Press,Urbana(1949).

[13]T.Fritz and R.Chaves,IEEE Trans.Inf.Theor.59(2013)803.

[14]R.Chaves,L.Luft,and D.Gross,New J.Phys.16(2014)043001.

[15]T.Fritz,New J.Phys.14(2012)103001.

[16]T.J.Osborne and F.Verstraete,Phys.Rev.Lett.96(2006)220503;M.Pawlowski andˇC.Brukner,Phys.Rev.Lett.102(2009)030403.

[17]R.Ramanathan,A.Soeda,P.Kurzy´nski,and D.Kaszlikowski,Phys.Rev.Lett.109(2012)050404.

[18]P.Kurzy´nski,A.Cabello,and D.Kaszlikowski,Phys.Rev.Lett.112(2014)100401.

[19]M.Pawlowski,Phys.Rev.A 82(2010)032313;J.Barrett,L.Hardy,and A.Kent,Phys.Rev.Lett.95(2005)010503.

[20]R.Ramanathan,T.Paterek,A.Kay,P.Kurzy´nski,and D.Kaszlikowski,Phys.Rev.Lett.107(2011)060405.

[21]R.Chaves,C.Majenz,and D.Gross,Nat.Commun.6(2015)5766.

[22]A.Fine,Phys.Rev.Lett.48(1982)291;Y.C.Liang,R.W.Spekkens,and H.M.Wiseman,Phys.Rep.506(2011)1.

[23]P.Kurzy´nski and D.Kaszlikowski,Phys.Rev.A 89(2014)012103.

[24]A.Cabello,S.Severini,and A.Winter,arXiv:1010.2163.

[25]A.Cabello,S.Severini,and A.Winter,Phys.Rev.Lett.112(2014)040401.

[26]R.Wright,inMathematical Foundations of Quantum Mechanics,ed.by A.R.Marlow,Academic Press,San Diego(1978)p.255.

[27]M.Grötschel,L.Lov´asz,and A.Schrijver,J.Combin.Theory B 40(1986)330;D.Knuth,Elec.J.Comb.1(1994)1.

[28]M.Grötschel,L.Lov´asz,and A.Schrijver,Geometric Algorithms and Combinatorial Optimization,Springer,Berlin(1988);L.Lov´asz,IEEE Trans.Inf.Theory 25(1979)1.

[29]B.Yan,Phys.Rev.Lett.110(2013)260406.

[30]A.Cabello,Phys.Rev.Lett.110(2013)060402.

[31]A.Ac´In,T.Fritz,A.Leverrier,and A.B.Sainz,Commun.Math.Phys.334(2015)533.

[32]A.Cabello,L.E.Danielsen,A.J.L´opez-Tarrida,and J.R.Portillo,Phys.Rev.A 88(2013)032104.

[33]R.Rabelo,C.Duarte,A.J.L´opez-Tarrida,M.T.Cunha,and A.Cabello,J.Phys.A:Math.Theor.47(2014)424021.