Coherent-State Approach for Majorana Representation∗

Hao-Di Liu(刘昊迪),Li-Bin Fu(傅立斌),and Xiao-Guang Wang(王晓光)

1Beijing Computational Science Research Center,Beijing 100084,China

2Center for Quantum Sciences and School of Physics,Northeast Normal University,Changchun 130024,China

3National Laboratory of Science and Technology on Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

4Zhejiang Institute of Modern Physics,Department of Physics,Zhejiang University,Hangzhou 310027,China

1 Introduction

The Majorana representation(MR),which provides an intuitive picture to study a physical system with a high dimensional projective Hilbert space,[1]has attracted revived attention in recent years.Despite being introduced about 80 years ago,this representation,which endows quantum state with visualization,has become an efficient tool to study the symmetric related feature of quantum system,such as spinor boson gases,[2−7]multilevel qubits,[8]and Lipkin–Meshkov–Glick model,[9−10]since it naturally provides an intuitive way to study the geometrical perspectives of these systems,e.g.,geometric phase,[11−16]and entanglement.[17−22]

As we know,a two-level pure state can be described by a point on the Bloch sphere,and its evolution is perfectly represented by the trajectory of the point on the sphere.However,it seems hard to extend this geometric interpretation to a higher dimensional quantum states,since it is difficult to visualize the trace in high dimensional space.Faced with this,the early ingenious work of Majorana told us that we can study the problem from a different perspective:including more points on the two-dimensional Bloch sphere instead picturing one single point on a high dimensional geometric structure.In MR,one can describe a spin-Jstate intuitively by 2Jpoints on the Bloch sphere.These points are called Majorana stars of the state.Therefore,the physics information of a spin state,such as dynamic evolution,geometric phase,mutiparticle entanglement,can be represented by these stars.

However,this elegant geometric representation can only be used to study a pure spin state which has SU(2)symmetry.With the increasing attention of MR,how to extend this representation to mixed states or pure states with other symmetries becomes a fascinating problem.Recently,Giraud et al.proposed a generalization to arbitrary spin-jmixed state of the MR in terms of tensors that share the most important properties of Bloch vectors based on covariant matrices introduced by Weinberg.[23]Moreover,for anyn-dimensional pure state,the parameterization process in Majorana representation can also be borrowed to definen−1 stars on the Bloch sphere,but the symmetry features carried by the state might not be properly presented.For example,the geometric phase of the states and their topological properties can also be studied by the stars,[16]but the entanglement of a multiparticle pure state can not be determined exclusively due to the arbitrary of base vector.This arbitrary can be fixed by certain symmetry,such as SU(2)symmetry corresponding to the symmetric qubit state.[12−13]Therefore,it is a natural question to ask whether a similar geometric representation can be found for a general pure quantum state without loss of symmetry information.Inspired by the relation between Majorana representation and Schwinger boson,we find the answer lies with the generators of the SU(2).For a particular symmetry described by a Lie group,similar with SU(2),its generators can always correspond to a set of ladder and number operators,which can determine a parameterize way of the state as in SU(2).However,the choice of the parameters in this way is not unique.A reference state is needed.

In this work,we present a new extension for the MR.Based on the definitions of generalized coherent states[24]with the ladder and number operators,we choose the coherent state as a reference state and propose a procedure of establishing representation like MR for an arbitrary symmetry.We show that this coherent-state approach for MR can not only be used to typical states like coherent states and squeezed vacuum states for a particular symmetry,such as Heisenberg–Weyl(HW),SU(2),and SU(1,1)symmetries,but also can reproduce the change of symmetry in the period evolution of a quantum state.In this respect,it provides an intuitive way to study the quantum system which carries a particular symmetry.Furthermore,we find that the same type of state in our coherent-state approach for MR based on the different coherent states of the different symmetries possess the same distribution of the stars on the Bloch sphere.

This paper is organized as follows.In Subsec.2.1,we introduce the MR and the coherent state in MR.Then,by using the coherent state and ladder operators,we establish a coherent-state approach for an arbitrary symmetry and obtain a new representation of their states by stars on the Bloch sphere in Subsec.2.2.In Sec.3 this coherentstate approach representation is applied to three particular symmetries of Heisenberg–Weyl,SU(2),SU(1,1),and obtain three star equations,respectively.In Sec.4,we investigate the squeezed vacuum states in these three symmetries by the stars in the coherent-state approach representation.In Sec.5,a nonlinear system is studied to illustrate our theory.A brief discussion and summary are given in Sec.6.

2 Majorana Representation and Its Coherent-State Approach

2.1 Majorana Representation

We first introduce the MR which was developed for spins.[1]A generic spin-jstate

where|n〉j≡ |j,−j+n〉,k=2j−n,andn,kare integers.It is instructive to write the above state under the two boson representation.Formally,the spin basis state|j,m〉corresponds to a two mode boson state|j+m,j−m〉.Consequently,in the form of boson creation operatorsˆa†andthe spin state|ψ〉(j)can be written as

Then,we meet a homogeneous polynomial of degree 2j

This can be further written as

wherez=−x/y.Then,by solving the following star equation

we may find 2jrootsz1,z2,...,zn.Finally,the polynomial(4)can be written as a factorized form

Using Eq.(6),the state|ψ〉(j)(2)becomes

There are 2jcomplex numberszkdetermined by Eq.(5).These numbers completely describe the state and can be geometrically described by 2jpoints on a plane or on a unit sphere via relation

whereθkandϕkare the spherical coordinates.Therefore,any spin state|ψ〉(j)and its evolution can be depicted by these points which are called Majorana stars.Substituting Eq.(8)into(7)leads to

where

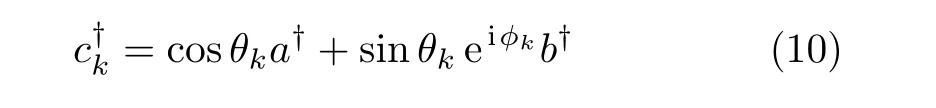
are also bosonic creation operators.This equation is another form of the spin state.

Now,as an example,we consider a spin coherent state(SCS)defined by[25−26]

whereηis a complex number.Comparing Eqs.(1)and(11),one finds

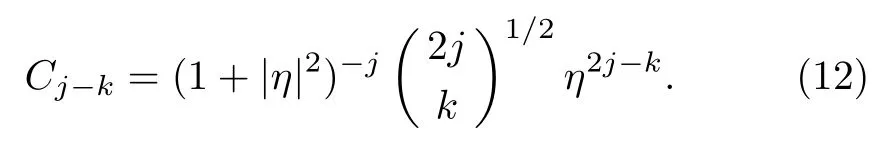
For finding the Majorana stars,substituting the above equation into Eq.(5)leads to

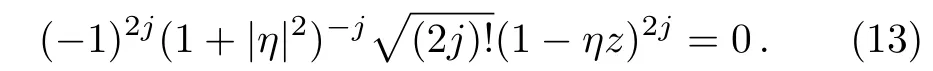
Thus,there are 2j-fold rootsz=η−1and 2jstars coincide in one single point on the Bloch sphere.There is still one point even in the case ofj→ ∞.So,we can choose the coherent state as a reference state when we intend to generalize the MR to more general systems including other finite or in finite systems.Next,based on the coherent state defined on a Lie group,we use the coherent-state approach to define new MR.

2.2 Coherent-State Approach

For the system with the symmetry of a Lie groupG,there exists a method to construct the coherent states.[24]The generatorsLiof groupGsatisfy the commutation relation

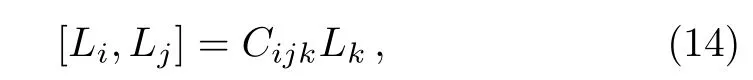
with structure constantsCijk.We may construct the ladder operatorsAandA†by the linear combination of{Lj}and define number operator N via a certainLλwhich satisfy

whereε1,ε2,...,εmis a sequence of positive numbers.

Using the creation operator,a generic state|ψ〉=Cm|m〉can be factorized as

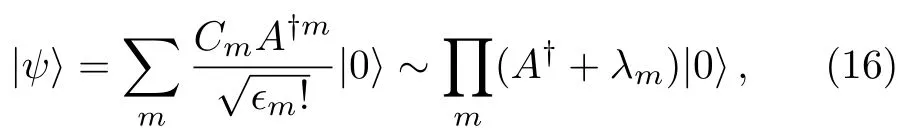
whereϵm!=ϵ1ϵ2···ϵmand the roots are determined via

Interestingly,if we decompose the complex numbersλmasλm=tan(θm/2)eiϕm,we can represent state|ψ〉as points(θm,ϕm)on the Bloch sphere as the stars in MR.However,the choice of ladder operators in Eq.(15)is not unique.Since,we can add any coefficient which is the function ofm,the new sequence ofwill still hold Eq.(15).This uncertainty of ladder operator seemingly become an obstacle to establish a symmetric-related representation.At this moment,we look back at the last subsection,the answer emerges naturally.The interesting representation that all the stars of the coherent state in MR accumulating on one point on the Bloch sphere provides us a natural reference to fix the choice of the ladder operatorA†.Therefore,we call this new representation as the coherent-state approach(CSA)for MR.

The coherent state can be defined as[24]

where|ψ0〉=|0〉is a fixed state which can be chosen as the eigenstate of some generatorˆLλand the symmetry-related operatorD(τ)is constructed by all the ladder operatorsAandA†.SinceD(τ)is a unitary operator,it can be written as

Note that,ladder operatorsAandA†are constructed by{Lj}.Therefore,we may have several pairs of ladder operators.For simplicity,we only consider one pair of ladder operators in this paper.

Technically,we can establish this new representation in three steps:

(i)Constructing the ladder operatorA†and the coherent state|α〉of the system with a particular symmetry.The operatorA†can be constructed by generators of the corresponding Lie group.[24]Suppose using the commutation relation between the ladder operatorsAandA†,the coherent state can be defined as

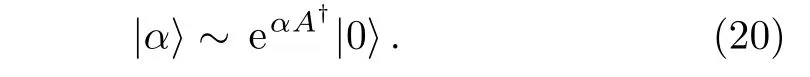
(ii)Using the coherent state as a reference to fix the ladder operator and Majorana points.To represent the coherent state as one point on the Bloch sphere,we define a nonlinear creation operator˜A†=f(N)A†to change the form of Eq.(20)into

Correspondingly,Eq.(16)becomes

Define the new complex coefficients asλm=tan(θm/2)eiϕm,we havenMajorana stars on the unit sphere. With this choice,one can guarantee that the stars for the coherent state coincide on one point,just like the case of spins.

(iii)Establishing the equation for Majorana stars.If we meet an in finite system,the cutoffcan be made as the all excitations for a physical state cannot be in finite.With this procedure,we next apply this CSA to some physical systems with particular symmetries.

3 Applications for Several Symmetries

3.1 Spin State for SU(2)Symmetry

First,we need to guarantee our CSA can reproduce the MR for SU(2)symmetry.The spin operatorsJx,Jy,Jzas the generators of SU(2)have the commutation relations

whereJ±=Jx± iJyare ladder operators.We have the following relations

Then,we arrive at

The coherent state for spins is well-defined and the related displacement operatorDj(τ)can be defined as

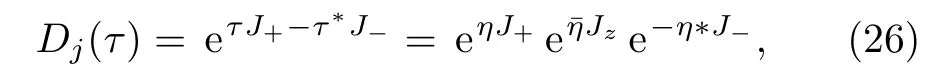
withη=tan|τ|eiarg(τ)and¯η=ln(1+|τ|2).The SCS is defined as

From Eq.(25),the general form of the spin state|ψ〉(j)(1)becomes

One may define the stars from the above form via the following star equation

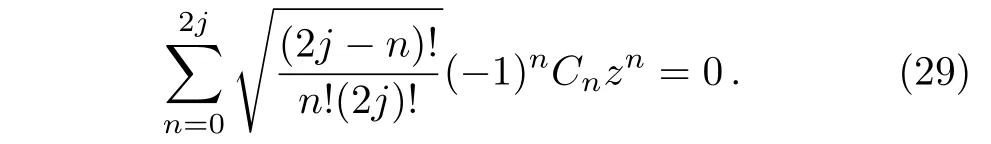
However,this equation is different from the star equation for spins(5).In other words,if we solve this equation for SCS,there will be 2jdifferent stars and cannot guarantee all stars coincide at a single point.

We solve this puzzle by introducing the nonlinear creation operator as

which has the property

Using the above equation and Eq.(25),letact on state|0〉j,we obtain

Then,the general state can be written as

From the above equation, finally,we obtain the star equation by considering−as a number

This equation is a little different but essentially has the same roots of the star equation(5).Obviously,from this form,all stars for the SCS(11)coincide.Next,using this coherent-state approach,we generalize MR from finite SU(2)systems to systems with in finite dimensions.

3.2 Single Mode Boson State for HW Symmetry

In a similar way with the above discussion,we consider the bosonic single-mode system which has HW symmetry.Its generators are the boson creation operatora†and annihilation operatoraand the unity operatorI,which satisfy the commutation relations

The ladder operatora†and bosonic number operator N=a†afor the Fock basis{|m〉}satisfy

Thus,a single mode boson state takes the form

The coherent state can be obtained by action of the displacement operator,

on the vacuum state.Then,the coherent state is given by

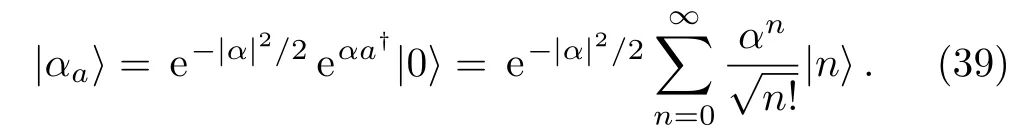
Different with the situation of SU(2),if we want to establish a geometric representation by stars,we need to truncate the in finite to a finite numberNc(since the excitations can not be in finite for a real physical state,the truncation is very physically reasonable,and the choice ofNcwill be shown in Fig.2).Define a nonlinear creation operator as

which obeys

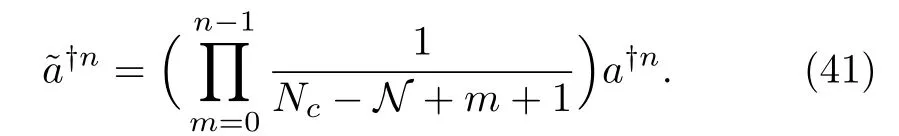
Acting on the vacuum state leads to

Thus,we obtain

Finally,we can write the general state(37)in terms of−as

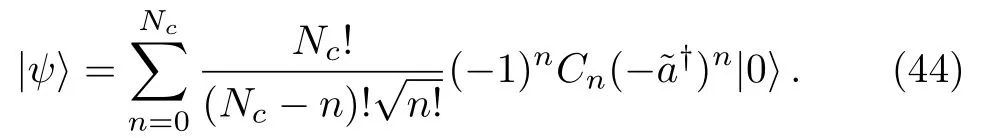
The star equation for the boson is given by

This star equation is applicable to all pure states of a boson.Obviously,for the coherent state,all the stars coincide.

3.3 State for SU(1,1)Symmetry

Another useful symmetry is SU(1,1)symmetry,which has been widely applied to study spin squeezing in quantum metrology[27−28]and some non-conservative physical systems.[29−32]Similar with group SU(2),group SU(1,1)also has three generatorsK1,K2andK3which satisfy

The irreducible representation is

withK±=(K1±iK2).It is easy to verify that the quadratic operator

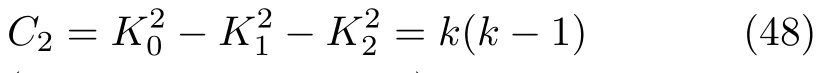
is invariant(the Casimir operator)with real numberk(Bargmann index).Basis vectors|k,m〉marked by an integermare the eigenvectors of the operatorK0.So,one can define a number operator Nk=K0−k,which satisfies

Substituting the coefficients of the coherent state(53)into the above equation,one finds again all the stars coincide.Thus,we have obtained three star equations,respectively for SU(2),HW,and SU(1,1)systems.Next,we apply these equations to real quantum states.

4 Squeezed Vacuum State in CSA

So far,we have presented how to establish the CSA for some kinds of symmetries.This coherent-state based method provides us a geometric tool to study properties of quantum states.We now consider a class of quantum state,i.e.,squeezed states.First,we consider the typical single-mode squeezed vacuum(SMSV)state

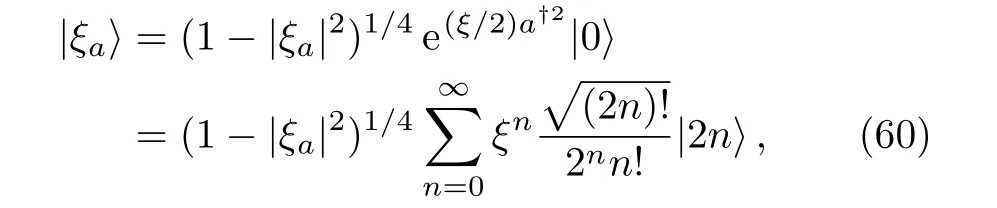
whereξais a complex number which satisfies|ξ|＜1.So,the coefficientC2nis given by

andC2n+1=0.Substituting the above equation into the star equation for bosonic system(45),we arrive at the star equation for the SMSV

where=−z2ξ/2.By solving the star equation,one finds[Nc/2]positive real roots(which can be proved by using Descartes’rule of signs)and then we haveNc(even)roots given by

So,the roots appear in a pairwise way with phases 3π/2 − Arg(ξ)/2 andπ/2 − Arg(ξ)/2 because only even states are involved.For oddNc,there exists an extra rootzk=∞corresponding to a star located on the south pole.

Similarly,one spin squeezed state for SU(2)symmetry is defined as[33−34]

One can also define the squeezed state for SU(1,1)system as

Substituting the coefficients in Eqs.(64)and(65)into Eqs.(34)and(59),respectively,we obtain two star equations for the two squeezed states as

where=−ξjz2/4j,=−ξkz2/2.Thus,we see that for the three squeezed states,the three star equations are essentially identical.If we choose other squeezed states,the star equations are different.

Fig.1 Bloch representation of CSA for the squeezed vacuum state with Nc=20 and(a)ξ=0,(b)ξ=0.001,(c)ξ=0.01,(d)ξ=0.9.

Fig.2 Bloch representation of CSA for the SMSV states with ξ=0.2 and different truncated numbers(a)Nc=10,(b)Nc=20,(c)Nc=30,and(d)Nc=50.

As the above three star equations become same for the states we have chosen,we here only consider bosonic squeezed vacuum state.For evenNc,we haveNc/2 pairs of roots with phases 3π/2−Arg(ξ)/2 andπ/2−Arg(ξ)/2 and thus the stars are all distributed on a big circle of the Bloch sphere and symmetric aboutzaxial,as shown in Fig.1.As the squeezing parameter|ξ|increases,the distribution of the stars varies from one overlapped points for the vacuum state|0〉(see Fig.1(a))to disperse points(see Figs.1(b)and 1(c)),and finally accumulate towards the north pole of the Bloch sphere(see Fig.1(d)).Thus,the increase of squeezing is intuitively represented by the moving of stars from south pole to north pole on the Bloch sphere.Furthermore,we study the influence of the truncation on the distribution of star.We also show the CSA representation of the SMSV state with different truncation in Fig.2.When the truncation is larger enough(Nc≥20),the distributions of stars are similar asNcincreases.

5 Example:Quantum Evolution in CSA Representation

To describe the quantum dynamics in CSA representation,we now consider a nonlinear Hamiltonian of the form[35]

whereωis the energy-level splitting for the linear part of the Hamiltonian,is a nonlinear operator(such as(a†a)2for HW which can be derived by a Kerr nonlinearity,[36])and Ω is the strength of the nonlinear term.This model can be used to describe all of the three symmetries HW,SU(2)and SU(1,1)with NF=N=a†a,NF=Nj=j+JZand NF=Nk=−k+K0,respectively.They all hold the relation N|m〉=m|0〉.Taking ΩN2as the interaction part,the time evolution operator in the interaction picture takes the form e−iΩtN2.If we choose the initial state as the coherent state

where|α〉corresponds to|αa〉,|αj〉,|αk〉for HW,SU(2)and SU(1,1),respectively,and the parameters are defined accordingly

Therefore,the state in timetcan be written as

Substituting Eq.(70)into Eqs.(34),(45),and(59)with the definition in Eq.(69),we have three equations of stars for HW,SU(2)and SU(1,1),respectively

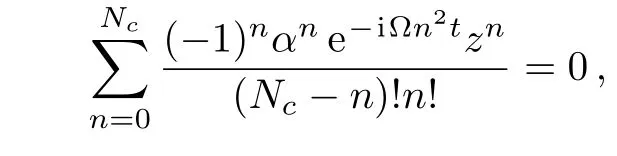
These three equations are identical whenNC=2j.Therefore,the distribution of the stars representing state|Ψ(t)〉in CSA representation for the three different symmetries are same.

It is easy to find that this state is periodic with a period 2π/Ω since|α,t+2π/Ω〉=|α,t〉.In one period,the state|Ψ(t)〉is very interesting at some special time points and corresponds to some special distributions of stars by solving Eq.(71).Att=0,the state is initially on the coherent state|α〉with all of the stars overlap on one point(as shown on the sphere at the original point in Fig.3);when the state evolves to time pointt=π/(4Ω),the state becomes the superposition of four different coherent states as[35]

By Eqs.(39)and(45),the star equation for this superposition of four coherent states becomes

withu≡αz.WhenNcis very large,by numerical simulation,we find that the arguments of the rootsunof this equation can only take four phasesπ/4,3π/4,5π/4,7π/4.Therefore,all the stars will be distributed on two orthogonal circles as shown on the sphere at the pointπ/4 in Fig.3.

As the state arrives att=π/(2Ω),the state turns into a cat state[35]

Using Eqs.(39)and(45),the star equation for this superposition of two coherent states becomes

Therefore,we have

Defineλ=Aeiϕ,we haveANc=1 and eiNcϕ=eiπ/2,which impliesA=1 andϕ=(2nπ+π/2)/Ncwithn=0,1,...,Nc−1.Thus,then-th root ofzsatisfies the relation

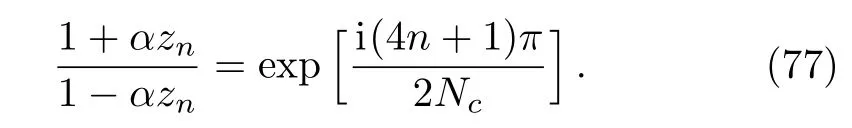
Therefore,the roots of Eq.(75)can be derived as

By the definitionzn=tan(θn/2)eiϕn,the spherical coordinates of the stars can be given by

The numerical results are shown on the sphere at the pointπ/2 in Fig.3,and the stars are distributed on one large circle.

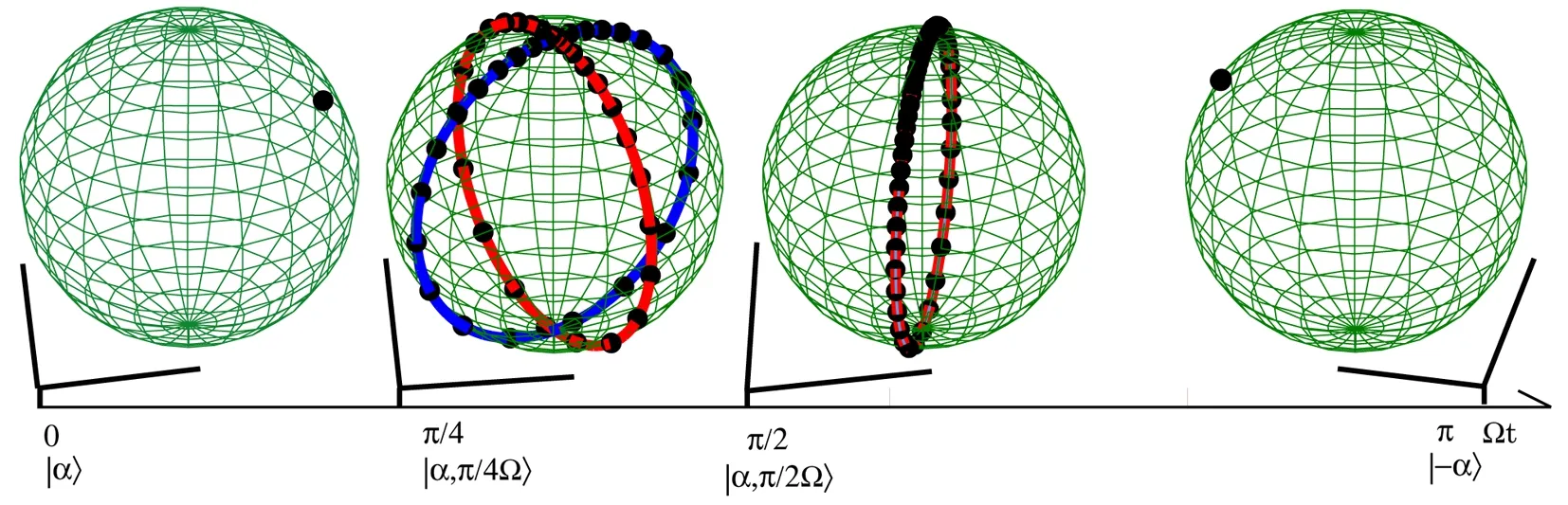
Fig.3 Bloch representation of CSA for the states|α,0〉,|α,π/4Ω〉,|α,π/2Ω〉,|α,π/Ω〉with HW,SU(2)and SU(1,1)symmetry,the parameters are chosen as α=2,n=50.

When the state evolves a half period,the state reverts to a single coherent state as

withncoincided stars on the Bloch sphere(as shown on the sphere at the pointπin Fig.3).Thus,the period evolution of a quantum state can be perfectly reflected by the period changes of stars on the Bloch sphere.Moreover,if 2πis dividable by Ωt,the stars for the state at this moment are distributed on several circles and the state can be written as the superposition of several coherent states.Furthermore,according to Eq.(71),these interesting phenomena can be observed in all of these three different symmetries.

6 Conclusions

The Majorana representation provides us a geometric tool to study the quantum states with SU(2)symmetry and their evolutions.Our study here is to show how can we extend this elegant method to the system with both finite and infinite dimensions.We found that the key of the answer is the coherent state.The definitions of coherent states in different kinds of symmetries inspired us a method to build the representation by ladder and number operators and provide a reference state to our representation.By study three different symmetries,we show this coherent-state approach of Majorana representation can well characterize squeezed states for different symmetries and the dynamical evolution of a quantum state.In this work,we only consider the situation with one pair of ladder operators.However,if there are more pairs of ladder operators,such as SU(3)symmetry,we may need a more complex geometric structure(like three correlated spheres),this will be discussed in our future work.Accordingly,there are also more symmetries like SU(N)(N＞2)need to be further studied with the CSA representation.

References

[1]E.Majorana,Nuovo Cimento 9(1932)43.

[2]Y.Kawaguchia and M.Ueda,Phys.Rep.520(2012)253.

[3]D.Stamper-Kurn and M.Ueda,Rev.Mod.Phys.85(2013)1191.

[4]B.Lian,T.L.Ho,and H.Zhai,Phys.Rev.A 85(2012)051606(R).

[5]X.L.Cui,B.Lian,T.L.Ho,B.L.Lev,and H.Zhai,Phys.Rev.A 88(2013)011601(R).

[6]R.Barnett,D.Podolsky,and G.Refael,Phys.Rev.B 80(2009)024420.

[7]A.Lamacraft,Phys.Rev.B 81(2010)184526.

[8]A.R.Usha Devi,Sudha,and A.K.Rajagopal,Quantum Inf.Process.11(2012)685.

[9]P.Ribeiro,J.Vidal,and R.Mosseri,Phys.Rev.Lett.99(2007)050402.

[10]P.Ribeiro,J.Vidal,and R.Mosseri,Phys.Rev.E 78(2008)021106.

[11]P.Bruno,Phys.Rev.Lett.108(2012)240402.

[12]H.D.Liu and L.B.Fu,Phys.Rev.Lett.113(2014)240403.

[13]H.D.Liu and L.B.Fu,Phys.Rev.A 94(2016)022123.

[14]S.Tamate,K.Ogawa,and M.Kitano,Phys.Rev.A 84(2011)052114.

[15]K.Ogawa,S.Tamate,H.Kobayashi,T.Nakanishi,and M.Kitano,Phys.Rev.A 91(2015)062118.

[16]C.Yang,H.Guo,L.B.Fu,and S.Chen,Phys.Rev.B 91(2015)125132.

[17]T.Bastin,S.Krins,P.Mathonet,M.Godefroid,L.Lamata,and E.Solano,Phys.Rev.Lett.103(2009)070503.

[18]P.Ribeiro and R.Mosseri,Phys.Rev.Lett.106(2011)180502.

[19]D.J.H.Markham,Phys.Rev.A 83(2011)042332.

[20]W.Ganczarek,M.Ku´s,and K.˙Zyczkowski,Phys.Rev.A 85(2012)032314.

[21]A.Mandilara,T.Coudreau,A.Keller,and P.Milman,Phys.Rev.A 90(2014)050302.

[22]D.Baguette,F.Damanet,O.Giraud,and J.Martin,Phys.Rev.A 92(2015)052333.

[23]O.Giraud,D.Braun,D.Baguette,T.Bastin,and J.Martin,Phys.Rev.Lett.114(2015)080401.

[24]A.M.Peremolov,Generalized Coherent State and Their Applications,Springer–Verlag,Berlin(1986).

[25]J.M.Radcliffe,J.Phys.A 4(1971)313.

[26]F.T.Arecchi,E.Courtens,R.Gilmore,and H.Thomas,Phys.Rev.A 6(1972)2211.

[27]J.Ma,X.G.Wang,C.P.Sun,and F.Nori,Phys.Rep.509(2011)89.

[28]K.Berrada,Phys.Rev.A 88(2013)013817.

[29]C.C.Gerry,Phys.Rev.A 35(1987)2146.

[30]J.R.Choi,Opt.Commun.282(2009)3720.

[31]J.W.Wu,C.W.Li,T.J.Tarn,and J.Zhang,Phys.Rev.A 76(2007)053403.

[32]D.Y.Song,Phys.Rev.A 68(2003)012108.

[33]H.Frahm and J.A.Holyst,J.Phys.:Condens.Matter 1(1989)3083.

[34]T.Nakajima and H.Aoki,Phys.Rev.B 56(1997)15549(R).

[35]B.Yurke and D.Stoler,Phys.Rev.Lett.57(1986)13.

[36]Z.R.Gong,H.Ian,Y.X.Liu,C.P.Sun,and F.Nori,Phys.Rev.A 80(2009)065801.