Lie Symmetry Analysis of the Inhomogeneous Toda Lattice Equation via Semi-Discrete Exterior Calculus∗

Jiang Liu(刘姜),Deng-Shan Wang(王灯山),,2,† and Yan-Bin Yin(尹彦彬)

1 Introduction

In the past years,much work has been done in extending the concepts and research methods of differential equations(PDEs)[1−12]to partial differential-difference equations(PDΔEs).[13−17]For example,the Lie symmetry method which is useful for doing similarity reductions of various PDEs,was developed and applied to calculate the symmetry groups and similarity solutions of some physically important PDΔEs.[18−24]Among the the study of Lie symmetries for PDΔEs,the well-known methods are Levi and Winternitz’s “intrinsic method”[18]and conditional symmetry method.[19]Subsequently,Quispel et al.[20]gave a somewhat different method to derive the Lie point symmetries of the Kac-van Moerbeke equation.Moreover,Jiang[21−22]observed that the nonintrinsic Lie symmetries do exist in certain PDΔEs,and proposed a mechanism for automating symmetry calculations for fairly general PDΔEs.

The classical Lie symmetry method has an equivalent geometric description which was proposed by Harrison and Estabrook[25]early. The main idea of this geometric approach[26−27]is based on exterior differential forms and Cartan’s formulation of differential equations,and the key point is to use the Lie derivatives of exterior differential forms. We[28]have extended the geometric approach[25−26]of Harrison and Estabrook to PDΔEs based on the discrete exterior differential technique,[29−31]also named semi-discrete exterior calculus.More recently,this technique was extended to study the(2+1)-dimensional Toda equation and discrete-time Toda equation,[32−34]respectively.

In this paper,we further extend the semi-discrete exterior calculus to the variable-coefficient PDΔEs such as the inhomogeneous Toda lattice equation in Ref.[35].It is shown that the semi-discrete exterior calculus is also very effective to investigate the Lie symmetries and similarity reductions of variable-coefficient PDΔEs.This paper is organized as follows:Section 2 presents the simple description of the semi-discrete exterior calculus.Sections 3 and 4 give the Lie point symmetries and similarity reductions of the inhomogeneous Toda equation by semi-discrete exterior calculus.Conclusions are proposed in Sec.5.

2 Semi-Discrete Exterior Calculus

In this section,a simple description of the semi-discrete exterior calculus is given following the pioneering work of noncommutative differential calculus.[29−31]A more detailed description can be found in Ref.[36]on algebra of function space of several discrete and continuous variables.

Letx=(m1,...,mk;x1,...,xr)be any point on the(k+r)-dimensional spaceM=Zk×Rr,whereZkis a lattice.Define A to be the algebra of complex valued functions onM.

For any function

define the forward difference of functionfon theµ-th discrete variablemµto be

whereEµis the forward shift operator of functionfonmµ,i.e.

With the definition of forward difference operator above in mind we can define the tangent space at pointx∈Mas

where Δµ(µ=1,2,...,k)are the forward difference operator and∂/∂xi(i=1,2,...,r)are the usual partial derivative operator.Correspondingly,the dual space of tangent spaceTM|x,i.e.the cotangent spaceT∗M|xis defined formally as

The exterior differential operatorddefined above has some other important properties as follow:

(i)dχµ=0,µ=1,2,...,k,

(ii)d(dxj)=0,j=1,2,...,r,

(iii)d(ω∧θ)=(dω)∧θ+(−1)degωω∧(dθ),

(iv)(df)(V)=V(f),forf∈A andV∈TM|x.

In order to develop the semi-discrete exterior calculus to do Lie symmetry analysis,the next step is to introduce the discrete contraction operatoriVas

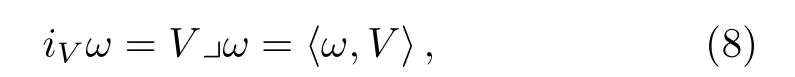
whereV=

Thus similar to the classical definition of Lie-derivative in Ref.[25],the semi-discrete Lie-derivative can be defined as

3 Lie Symmetry of Inhomogeneous Toda Equation

The inhomogeneous Toda equation is given by[35]

such that they form a closed ideal

Let us introduce the is ovector field on the sevendimensional spaceN,i.e.

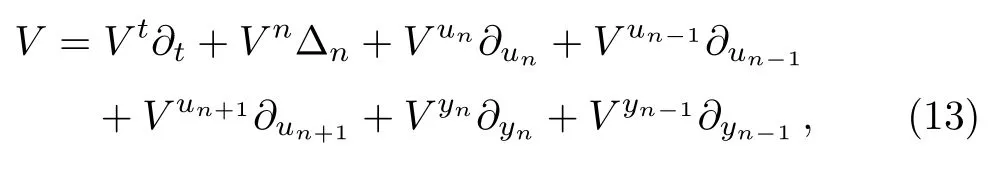
which is a tangent vector field onN.Then consider the Lie derivatives ofα1,α2,andβ,and require them to be a linear combinations of the differential forms in I,i.e.

wheref1,f2,g1,g2,h1,h2,ηare zero forms andξ1,ξ2are one forms to be determined.

Omitting the process of calculations,it is easy to obtain the following equations of the coefficients of isovector fieldVas

where

Finally,it is obvious thatLVdα1andLVdα2are already in the ideal I. Thus we need not to write the separate equations for them. By solving Eqs.(17)–(19),we have the expressions of functionsVj(j=t,n,un,un−1,un+1,yn,yn−1)as

wherea,b,c,anddare arbitrary constants.

Thus the Lie algebra of in finitesimal symmetries for the inhomogeneous Toda equation(10)is spanned by the following vector fields:

Applying the commutator operator[Vi,Vj]=ViVj−VjVifor any two vectorsViandVj,we get the commutator relations listed in Table 1 with the(i,j)-th entry indicating[Vi,Vj](i,j=1,2,3,4).It is seen from Table 1 that L=span{V1,V2,V3,V4}is a four-dimensional Lie algebra withV4a central element.

Table 1 Lie bracket.

All four-dimensional real Lie algebras were classified completely by Patera and Winternitz[37](see also Ref.[38]). They found all classification into equivalence class under group of inner automorphism,and also used the idea of normalization,which guarantees the constructed optimal system of subalgebras is unique up to the isomorphic.

In what follows,we adopt the convention in Ref.[36]that the symbol{e1,e2,...,en}denotes the vector space spanning by spanninge1,e2,...,en. It is known that the algebraA4,8is solvable and spanned by generatorse1,e2,e3,e4,with non-zero commutation relations

The Lie algebraA4,8is an indecomposable Lie algebra and can be written as semidirect sumsA4,8={e4}■NwhereNis a three-dimensional idealN={e1,e2,e3}and of typeA3,1.Our Lie algebra L is isomorphism to the Lie algebraA4,8by taking the generators as the form

Following the classi fication in Patera and Winternitz,[37]the optimal systems of subalgebras to the algebraA4,8are listed in Table 2,whereλ/=0,ϵ= ±1.

Table 2 The optimal system of subalgebras hiof A4,8.

Thus we obtain the one-,two-and three-dimensional optimal systems of L by the Lie algebra isomorphism from L toA4,8as follows:

Theorem 1The one-dimensional optimal system of Lie algebra L involves five subalgebras,i.e.{V4},{V2},{V3},{V2+ϵV3},{V1+λV4},two-dimensional optimal system involves six subalgebras,i.e.{V2,V4},{V3,V4},{V2±V3,V4},{V1,V4},{V2,V1+λV4},{V3,V1+λV4},and three-dimensional optimal system involves three subalgebras,{V2,V3,V4},{V1,V2,V4},{V1,V3,V4}whereλ/=0,ϵ= ±1.

4 Similarity Reductions

In Sec.3,the in finitesimals of the inhomogeneous Toda equation(10)have been determined by semi-discrete exterior calculus,which form a four-dimensional Lie algebra L.Moreover,the one-,two-and three-dimensional optimal systems of Lie algebra L are given.The optimal systems and the combinations of in finitesimals can be used to do similarity reductions to the inhomogeneous Toda equation(10).In what follows,we mainly consider the similarity reductions based upon the symmetry vectorsV2+λV3andaV1+bV2+cV3+dV4(wherea,b,c,dare constants),respectively.

4.1 Reduction Based on Vector V2+λV3

For the symmetry vectorV2+λV3,solving the characteristic equation

the similarity variables can be found as

Thus the inhomogeneous Toda equation(10)can be reduced to a difference equation in only one independent variablen

Taking the dependent variable transformation

then difference equation(26)becomes

which becomes

when puttingzn=yn/yn+1.

4.2 Reduction Based on Vector aV1+bV2+cV3+dV4

For the symmetry vectoraV1+bV2+cV3+dV4,solving the characteristic equation

the similarity variable can be found as

Thus the inhomogeneous Toda equation(10)can be reduced to a difference equation in only one independent variablen

Taking the dependent variable transformation

then difference equation(32)becomes

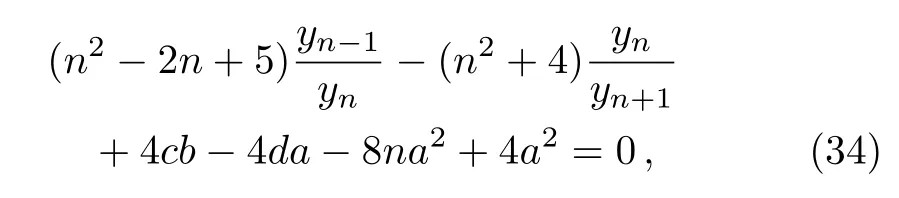
which becomes

when puttingzn=yn/yn+1.

It is remarked that the difference equation(35)becomes Eq.(29)by settinga=d=0,b=1,andc=λ.

5 Conclusion and Remarks

In conclusion,the semi-discrete exterior calculus is extended to the variable-coefficient partial differentialdifference equation,i.e.the inhomogeneous Toda lattice equation.The isovector fields are obtained,which form a four-dimensional Lie algebra.The one-,two-and threedimensional optimal systems of this Lie algebra are proposed.Finally,two isovector fields are used to do the similarity reductions of the inhomogeneous Toda lattice equation.The semi-discrete exterior calculus can also be used to investigate the Lie symmetries of other variablecoefficient partial differential-difference equations.

References

[1]M.J.Ablowitz,SIAM.Rev.19(1977)663.

[2]V.B.Matveev and M.A.Salle,Darboux Transformation and Solitons,Springer,Berlin(1991).

[3]P.J.Olver,Applications of Lie Groups to Differential Equations,GTM 107,2nd ed.Springer,New York(1993).

[4]W.X.Ma,Phys.Lett.A 301(2002)35.

[5]S.Y.Lou,J.Math.Phys.41(2000)6509;X.Y.Tang and S.Y.Lou,Chin.Phys.Lett.19(2002)1.

[6]Y.Chen and Z.Z.Dong,Nonlinear Anal.71(2009)810.

[7]S.H.Meng,L.Xu,and L.Chen,J.Syst.Sci.Infor.4(2016)258.

[8]L.Wang and S.C.Guo,J.Syst.Sci.Infor.4(2016)560.

[9]X.Lü,Chaos 23(2013)033137.

[10]S.F.Tian and H.Q.Zhang,Stud.Appl.Math.132(2013)212.

[11]X.Y.Wen and Z.Yan,Commun.Nonlinear Sci.Numer.Simulat.43(2017)311.

[12]B.Ren,Phys.Scr.90(2015)065206.

[13]M.J.Ablowitz,B.Prinari,and A.D.Trubatch,Discrete and Continuous Nonlinear Schrödinger Systems,Cambridge University Press,Cambridge(2004).

[14]X.Y.Wen,Z.Y.Yan,and B.A.Malomed,Chaos 26(2016)013105.

[15]G.F.Yu and Z.W.Xu,Phys.Rev.E 91(2015)062902.

[16]G.F.Yu,Stud.Appl.Math.135(2015)117.

[17]H.M.Li,B.Li,and Y.Q.Li,J.Math.Phys.53(2012)043506.

[18]D.Levi and P.Wintemitz,Phys.Lett.A 152(1991)335.

[19]D.Levi and P.Winternitz,J.Math.Phys.34(1993)3713.

[20]G.R.W.Quispel,H.W.Capel,and R.Sahadevan,Phys.Lett.A 170(1992)379.

[21]Z.H.Jiang,Phys.Lett.A 240(1998)137.

[22]Z.H.Jiang,J.Math.Anal.Appl.227(1998)396.

[23]W.Ding and X.Y.Tang,Commun.Theor.Phys.41(2004)645.

[24]S.F.Shen,Z.L.Pan,and J.Zhang,Commun.Theor.Phys.42(2004)805.

[25]B.K.Harrison and F.B.Estabrook,J.Math.Phys.12(1971)653.

[26]B.K.Harrison,SIGMA 1(2005)001.

[27]D.S.Wang and Y.B.Yin,Comput.Math.Appl.71(2016)748.

[28]H.J.Li,D.S.Wang,S.K.Wang,K.Wu,and W.Z.Zhao,Phys.Lett.A 372(2008)5878.

[29]A.Connes,Noncommutative Geometry,Academic Press,New York(1994)

[30]H.Y.Guo,K.Wu,and W.Zhang,Commun.Theor.Phys.34(2000)245.

[31]K.Wu,W.Z.Zhao,and H.Y.Guo,Sci.China Ser.A:Math.49(2006)1458.

[32]N.Lv,J.Q.Mei,and H.Q.Zhang,Int.J.Geom.Meth.Mod.Phys.9(2012)1220014.

[33]Q.Ding and S.F.Tian,Rep.Math.Phys.74(2014)323.

[34]X.Y.Jia and N.Wang,Chin.Phys.Lett.26(2009)1.

[35]D.Levi and O.Ragnisco,J.Phys.A 24(1991)1729.

[36]Y.Q.Bai,K.Wu,H.Y.Guo,and W.Z.Zhao,Commun.Theor.Phys.48(2007)591.

[37]J.Patera and P.Winternitz,J.Math.Phys.18(1977)1449.

[38]L.V.Ovsiannikov,Group Analysis of Differential Equations,Nauka,Moscow(1978);English Translation by W.F.Ames,ed.,Published by Academic Press,New York(1982).