深度体验 适时提炼 清晰表达
——小学生抽象思维能力培养例谈
2017-05-12袁敬丰张晓霞郑云芳
◎袁敬丰 张晓霞 郑云芳
深度体验 适时提炼 清晰表达
——小学生抽象思维能力培养例谈
◎袁敬丰 张晓霞 郑云芳
学会思维,是数学学科所应关注的核心素养。抽象是一种重要的思维方法,它贯穿于小学生数学学习的始终。那么,在数学课堂教学中如何培养学生的抽象思维能力呢?现以苏教版《义务教育教科书·数学》六年级《正比例的意义》一课为例说明进行。
一、认识相关联的量
师:孩子们,老师第一次来到你们这个城市,昨天在街上溜达了下,感觉真是漂亮,到处都是高楼大厦,(屏显高楼图)仔细观察,你看到了什么?
生1:我看到大楼越来越高。
师:那大楼的层数呢?
生2:大楼的层数在一层一层地增多。
师:把这两句话连起来说一说好吗?
生2:大楼的层数在增多,楼的高度也越来越高。
师:说得真好!随着楼的层数的增多,楼的高度也越来越高。在数学上我们把这样有关系的两种量叫做相关联的量。在下面的场景中你也能找到相关联的量吗?(出示四幅图)

生3:我们去超市买苹果的时候买的数量越多,要付的钱就越多,买的数量越少,要付的钱就越少,所以数量和总价是两种相关联的量。
师:看图2,老师带这么多钱买苹果,用去的少,剩下的就多;用去的多,剩下的就少。
生4:用去的钱和剩下的钱是两种相关联的量。
生5:在太阳底下,物体越高,影子越长,所以物体的高度和影子的长度是两种相关联的量。
生6:从第四幅图,我知道杯子的粗细和水的高度是两种相关联的量。
师:你说的杯子的粗细,其实就是杯子的底面积。
生7:杯子的底面积和水的高度是两种相关联的量。
师:在这些图中我们都找到了两种相关联的量,相关联,你理解了吗?
生8:一种量变化,另一种量也跟着变化。
师:这个“跟着”说得多好啊!可见这两种量的关系得有多亲密啊!
理解正比例的意义,首先要理解什么是相关联的量。教师选取学生熟悉的楼房为话题,自然调动起学生的生活经验:楼房的高度随着层数的变化而变化,楼层数越多,楼房越高。看似无意的闲聊中,相关联的概念已萌发。接着出示四幅学生生活中常见的场景图,目的是让学生借助知识和生活经验并通过观察、比较、分析、想象等活动,进一步理解什么是相关联的量,培养学生的判断、推理能力。
二、探究正比例的意义
(一)探究路程和时间的变化规律
师:老师在汽车里程表上采集到这样一组数据,仔细观察,猜一猜这里路程的变化可能会跟什么有关系?

路程(千米) 8 0 1 0 0 1 6 0 2 0 0 2 4 0 2 5 0 ……
生1:可能跟开车的速度有关系。
生2:可能跟开车的时间有关系。
师:用上我们刚刚认识的“相关联”来说一说?
生1:路程和速度是两种相关联的量。
生2:路程和时间是两种相关联的量。
师:继续看这张表格,现在你认为路程更有可能跟谁相关联?
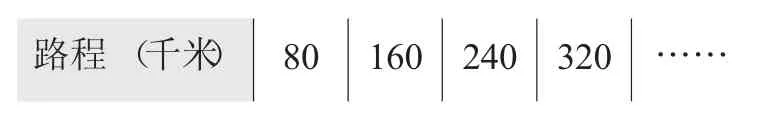
路程(千米) 8 0 1 6 0 2 4 0 3 2 0 ……
生3:这里路程的变化更可能跟时间相关联。
师:猜得真准,仔细观察表格,你有什么发现?可以先在作业纸上写一写,然后在小组里互相说一说。

时间(小时)1 2 3 4路程(千米)8 0 1 6 0 2 4 0 3 2 0…………
学生独立思考,小组交流后进行全班交流。
生1:时间在变多,路程也在变多。
生2:从左往右看时间在变多,路程也跟着在变多。从右往左看时间在变少,路程也跟着在变少。
师:从不同角度发现两种量之间的变化,说的真全面。
生3:路程和时间是两种相关量的量。
师:一句话就把刚才这两位同学的发现概括地表达出来,学了就能用,真好.
师:刚才这几位同学都看到了这两种量的变化情况,你们也发现了吗?还有什么不同的发现吗?
生4:我发现路程和时间不但是两种相关联的量,而且速度是始终不变的。
师:你的发现与众不同,请你再大声说一遍。都听到了吗?看一看,想一想,她说的对吗?
师:还有的同学还在思考,就请你当小老师来讲一讲你是怎么发现速度不变的?
生4:80÷1=80160÷2=80 240÷3=80……这里的商就是速度,始终没有变。
师:刚才这两位同学都能用联系的眼光从变化中看到了不变,真了不起!他们在举例证明的时候不管是求商还是写比,都注意到80和1为一组,160和2为一组……这又给我们什么启示呢?
生6:路程除以相对应的时间,求出的值才有意义。
师:回顾刚才的学习过程,你能把你的发现作一个简单的总结吗?
生7:路程是跟着时间的变化而变化的。
生8:路程和时间是两种相关联的量,它们的比值始终不变。
师:两种相关联的量在不断地变化,这是我们看到的现象;而相对应的数的比值一定,这是我们发现的规律。是什么原因使得它们的比值始终不变呢?我们需要探究规律背后的真相了。
这个问题有点难度,我们一起来吧,从1小时80千米开始,时间从1到2扩大2倍,相应的路程也从80到160扩大2倍。
生9:时间从1到3扩大3倍,路程也从80到240也扩大了3倍。
生10:我知道了,这里其实就是比的基本性质。
生11:也可以看作是分数的基本性质。
生12:还可以看作商不变的规律。
师:现在大家明白比值为什么不变了吧?学数学我们就要这样知其然,更要知其所以然。
师:刚才我们从不同的角度来观察这张表格,现在把大家的发现来总结一下,请你想一想,填一填,说一说。
(二)探究楼层数与楼的高度的变化规律
师:你能用同样的方法来研究楼的高度和层数之间的规律吗?
屏显下表。

楼层数(层)4 5楼的高度(米)1 3 2 6 3 9 1 2 1 5
学生思考后回答:
生1:楼层数和楼的高度是两种相关联的量。
生2:楼的高度和楼层数的比值也是一定的。
师:这个比值是多少?表示什么意思?
生3:楼的高度和楼层数的比值是3,表示每层楼的高度。
师:能写出它们之间的关系式吗?

3.引导抽象正比例的意义
师:这是我们刚才研究的两组相关联的量(屏显)。
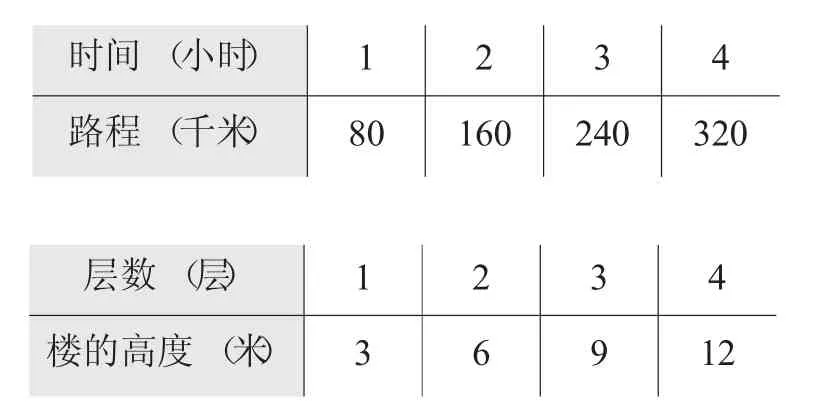
时间(小时)1 2 3 4路程(千米)8 0 1 6 0 2 4 0 3 2 0层数(层)4楼的高度(米)1 3 2 6 3 9 1 2
师:在这里,我们把路程和时间就叫做成正比例的量;同样的,楼的高度和层数也叫做成正比例的量。看着这两张表格想一想:怎样的两种量就是成正比例的量?请大家先独立思考,然后在小组里说一说。
这是学生第一次真正探究成正比例的两个量之间的关系。教师采取细思慢想的策略,首先出示一张数据无规律的表格让学生根据生活经验猜想路程和什么相关联,然后出示一张数据有规律的表格让学生猜想路程和什么相关联,自然地引导学生从生活经验走向数学思考。接着,进一步引导观察、思考路程是怎样随着时间的变化而变化的,再组织组内交流、全班反馈。学生的思维得以沉潜,并在思维的碰撞中渐渐地发现路程与时间的变化规律。教师的适当追问、讲解,凸显了对应的量,渗透了比较的方法和对应思想。教师引导学生用联系的观点多角度探究比值一定的深层原因,促使学生自主构建、完善知识结构,思维得以通透。在学生研究了路程与时间的变化关系后,教师再次放手让学生探究楼层数与楼的高度的关系,旨在丰富学生的感知,加深学生的体验,有利于学生归纳、发现正比例的意义。通过路程与时间、楼层数与楼的高度变化规律的研究,学生已经积累了一定的感性认识,教师适时地集中出现两张表,引导学生进行观察、比较、分析,舍弃其数据不同、现象不同等非本质属性,概括正比例的意义。
三、运用新知,解决问题
师:认识了正比例,我们怎么去判断两种量是不是成正比例呢?请大家来试一试。出示:购买一种铅笔的数量和总价如下表:

数量(支) 1 2 3 4 5 ……总价(元) 0 . 4 0 . 8 1 . 2 1 . 6 2 ……
(1)观察上表,说说总价是随着哪个数量的变化而变化的?
(2)写出几组对应的总价和数量的比,并比较比值的大小。
(3)这个比值表示的实际意义是什么?你能用式子表示它与总价、数量之间的关系吗?
(4)铅笔的总价和数量成正比例吗?为什么?
师:相对于你们得到的结论,老师更感兴趣的是:你们是怎么判断的?
生1:数量在变总价也在变,数量和总价是两种相关联的量。
生2:数量和总价是两种相关联的量,而且它们的比值也是一定的都是0.4,表示这种铅笔的单价。

师:有了判断两种量成正比例的方法,下面就让我们牛刀小试一下。(屏显课初的四幅图)刚才我们在这些图中都找到了两种相关联的量,他们都成正比例吗?为什么?
师:生活中,像这样成正比例关系的两种量还有很多很多,请在小组里互相说一说?(略)
师:数学的神奇就在于简洁,你能想办法用字母来表示正比例关系吗?
师:在数学上我们一般用y和x来表示像这样的两种相关联的量,用k来表示它们的比值,这样正比例关系式我们就可以写成=k(一定)。
师:学习正比例有什么用呢?

时间1 2 3 4 6路程8 0 1 6 0 2 4 0 3 2 0()时间(小时)1 2 3 6路程(千米)8 0 1 0 0 2 1 0()
师:从这两张表格中,我们都可以预测出6小时行驶的路程吗?
生8:第一张表格可以预测出行驶的路程。
师:为什么呢?
生9:第一张表格中路程和时间成正比例,第二张表格中路程和时间不成正比例。
师:那我们来预测下6小时可行多少千米,行800千米需要多少小时?

时间1 2 3 4 6路程8 0 1 6 0 2 4 0 3 2 0()()8 0 0…………
师:学习正比例可以帮助我们进行合理的预测、判断。
这里的练习,旨在引导学生运用正比例的意义对生活中的问题进行分析判断、预测,加深学生对正比例意义的理解,培养学生的数感、数据分析观念以及解决实际问题的能力。让学生用字母表示关系式,是学生抽象思维的再一次具体表现。教师对学生思考过程与方法的追问,体现教师不仅关注学生思维的结果,更关注学生思维的过程以及能否有条理地表达。
四、回顾反思、积累经验
师:学到这里,能说说这节课的收获吗?
生1:我知道了什么叫做正比例。
生2:我学会了如何去判断两种量成正比例。
生3:我知道了不是所有的相关联的两种量都是成正比例的量。
师:老师为同学们有这么多收获感到高兴。我们再一起来看课题,正比例,哪个词我们特别熟悉啊?
生:比例。
师:那这个“正”字我们该怎么理解呢?
师:在刚才的例题中,路程和时间是两种相关联的量,如果老师这样表示时间,→(动态演示)时间在变,路程会随着它一起变→。现在理解这个“正”字了吗?
如果我把时间这样表示,→路程这样表示↑,我们又会以怎样的方式来表达他们之间的关系呢?下节课我们来研究。
这一环节,通过回顾学习过程,帮助学生积累观察、比较、推理等数学基本活动经验和思维经验。对课题中“正”字的提问,使学生的思维从深入走向浅出,最后一问,则使学生带着问题走出教室,为下节课学习正比例的图像埋下伏笔。
丰富而有深度的体验是抽象的基础。感知越丰富、体验越深刻,才越有利于学生抽象出知识的本质。所以,感知的内容要是学生喜闻乐见的,能唤起他们已有的生活经验和认知基础;感知的步子要小一些,每一步要坚实,不能浮光掠影;感知的时间要充足,要能让学生静得下心,细思慢想;感知的氛围要宽松民主,让学习像呼吸一样自然;感知的方法要多样,要设计观察、操作、比较等有效的数学学习活动引领学生探究发现。
适时比较提炼是抽象的关键。适时,需要教师精准地把握学情、调控教学,过早,势必有火候不到、生拉硬拽的感觉,过迟,学生往往会被过多的非本质属性所牵绊,抓不住本质。这个阶段,学生往往会看山是山,看水是水,教师要注意培养学生跳出一个个具体的情境,抽取出共同的、本质的属性而舍弃个别的、非本质的属性。
准确清晰地表达是抽象的外显结果。语言是思维的外壳,想得清楚,方能说得明白。把思维的过程用一定的语言形式表达出来,思维会更加清晰,对知识的理解会更加深刻。教学中,教师要组织学生充分地交流,一方面可以了解学情,调控教学,另一方面,可以促进学生思维的碰撞,在碰撞中完善认知;要鼓励学生个性化地表达,可以是文字、符号、图表等多种形式。
(作者单位:江苏省盐城市亭湖区教研室,盐城市亭湖新区实验学校)
(责任编辑:杨强)
