卤素阴离子和取代苯间Anion－π作用强度的快速计算

王晓雯 李 蕾 王长生

卤素阴离子和取代苯间Anion－π作用强度的快速计算

王晓雯 李 蕾 王长生*

(辽宁师范大学化学化工学院，辽宁大连116029)

本文提出了一种可快速计算Anion－π作用强度的方法。该方法包含静电、极化和范德华作用。我们将取代苯的C≡N、C―F和C―H化学键作为键偶极，通过阴离子和取代苯的键偶极间相互作用来计算静电作用，根据键偶极大小随着环境变化而改变来计算极化作用。文中所需参数由模拟CCSD(T)/CBS势能曲线而确定。将本文方法应用于一系列卤素阴离子和取代苯间的Anion－π相互作用的快速计算，并与CCSD(T)/ CBS方法的计算结果进行了比较。计算结果表明，本文方法得到的势能曲线与CCSD(T)/CBS势能曲线符合很好；与CCSD(T)/CBS方法的计算结果比较，本文方法预测平衡分子间距离均方根偏差为0.004 nm，相互作用能均方根偏差为2.81 kJ·mol－1，说明本文方法合理可靠。本文方法可望在相关分子材料设计模拟领域发挥作用。

Anion-π作用；静电作用；极化作用；键偶极；相互作用能

1 Introduction

Noncovalent interactions play crucial roles in biochemistry1－3, supramolecular chemistry4－6,material chemistry7－9,and catalytic chemistry10－12.Noncovalent interactions involving aromatic rings such as anion－π,cation－π,and π－π interactions are important in biological and chemical recognition and also in nanomaterials, organic crystals,biomolecules,and clusters13－18.Among various noncovalent interactions involving aromatic rings,anion－π interactions were widely neglected owing to expected electrostatic repulsion between arene π-system and anion.However,four classical reports were published in 2002 proposing that there exist anion-π complexes with the anion lying above the ring center of arene π-system such as C6F6,1,3,5-triazine,C6H3CN3,C6H3F3and other aromatic compounds19－22.Anion－π interactions were further proved to exist by numerous X-ray structures and Cambridge Structural Database(CSD)search22－25.Complexes of substituted benzenes and halide anions,with anions centered over the face of the benzene ring,are frequently used to investigate anion－π interactions computationally among the model systems7,26－32.For instance,Kim et al.26found that the anion－π interactions are sometimes as strong as the cation－π interactions.Wheeler and Houk29examined the effects of substituents on the strength of benzene binding to chloride anion centered over the face of the benzene ring.Garau et al.31investigated the additivity of anionπ interactions involving chloride anion and bromide anion by using the MP2/6-31++G(d,p)method.Frontera et al.32investigated the synergic effects between anion－π,cation－π and π－π interactions involving F－,Cl－and Br－and found that cation－π and/or anion－π interactions have a very strong influence on π－π interactions.The importance of anion－π interactions is also found in many chemical and biological processes2.

For anion-π systems,the use of a theoretical treatment that takes into account the electron correlation is usually essential27,28,31.The CCSD(T)/CBS method is regarded as the“golden-standard”method due to its high quality accuracy for both covalent and noncovalent systems33.Unfortunately,the high-quality CCSD(T)/ CBS method are limited and even prohibited when applied to medium or large systems.

In this paper,a simple scheme is proposed to rapidly estimate the equilibrium intermolecular distances and interaction energies for anion-π complexes.Many reports have shown that anion－πinteractions with strong electron-donating groups are positive,and anion－π interactions with strong electron-withdrawing groups are negative17,19,29.It is great of significance to do research about the anion-π complexes with strong electron-withdrawing groups in supramolecular chemistry and molecular recognition1,2.Therefore, we chose two classical strong electron-withdrawing substituents (CN,F)(Fig.1(a))to develop our model by simulating anion－π interactions.Simulations on anion－π interactions manifest that the equilibrium intermolecular distances and interaction energies evaluated via our scheme agree well with those produced via the very expensive CCSD(T)/CBS calculations,indicating that the scheme proposed here is reasonable and useful.

2 Computational details

2.1 Benchmark interaction energy

For anion-π complexes considered in this work,the interaction energies produced via the high-quality CCSD(T)/CBS method were taken as the benchmark.The computational formula of the CCSD(T)/CBS total energy E[CCSD(T)/CBS]is as following:

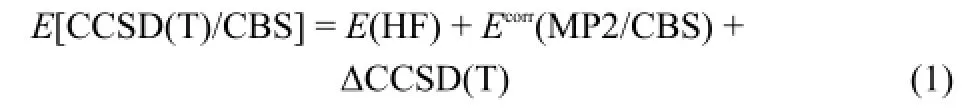
Here,we used aug-cc-pVQZ basis set to calculate the Hartree-Fock energy E(HF).The CBS limit of the MP2 correlation energy Ecorr(MP2/CBS)was obtained by extrapolating from the aug-ccpVTZ to aug-cc-pVQZ basis set using Helgaker′s formula34.The correction energy ΔCCSD(T)is estimated via Eq.(2).

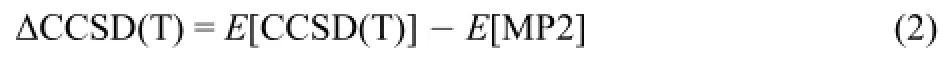
The aug-cc-pVDZ basis set is used to calculate the CCSD(T) energy E[CCSD(T)]and the MP2 energy E[MP2]because it has been shown that the ΔCCSD(T)correction obtained by using augcc-pVDZ basis set exhibits errors of no more than 0.4 kJ·mol－135.

We calculated the interaction energy between a substituted benzene and an anion via the CCSD(T)/CBS method.We moved the anions along the axis(the axis is defined here as the C6 axis of the benzene)in order that the distance between them was 5.0, 3.0,2.0,1.5,1.25,1.1,1.05,0.95,and 0.9 times the equilibrium value to obtain the CCSD(T)/CBS interaction potential energy curves35.All ab initio calculations were performed by Gaussian 09 program36.

2.2 Empirical model

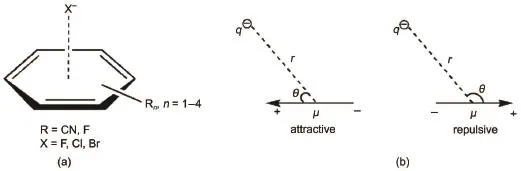
Fig.1 (a)Anion-π complexes studied in this work;(b)charge－dipole interaction model

It is believed that the major contributions to the anion－π in-teractions arise from electrostatics,polarization and dispersion interactions26,37.According to the believes,Eq.(3)is here proposed to rapidly estimate the interaction energies of anion-π complexes.

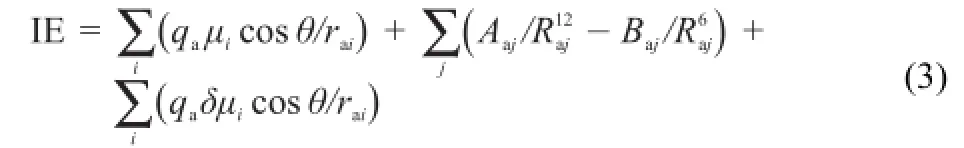
In the 1st term of Eq.(3),μiis the ith bond dipole moment of the molecule,qais the charge of the anion,raiis the distance between the anion and the ith bond dipole moment center,and θ is the angle (Fig.1(b)).We use the 1st term of Eq.(3)to estimate the electrostatic interactions.The electrostatic contribution can be easily obtained if the bond dipole moment μiand the relative orientation of anion and dipole is known.

There are various expression forms to calculate the van der Waals interactions38.We use the 2nd term of Eq.(3)to evaluate the van der Waals interactions whereand εaare the van der Waals parameters.

When an ion and a molecule are getting close each other,polarization happens.We use the 3rd term of Eq.(3)to estimate polarization contribution.Here,δμiis estimated via δμi=di·(qdqm)where diis the bond length,qmand qdcorrespond respectively to the partial charges of H,N,or F atom in the substituted benzene molecule and in the anion-π complex.

2.3 Parameterization

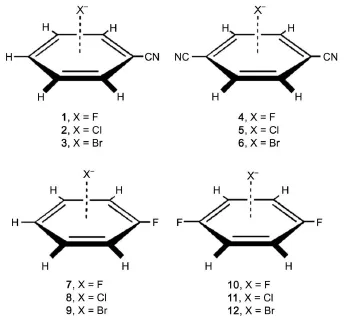
Fig.2 Training anion-π complexes

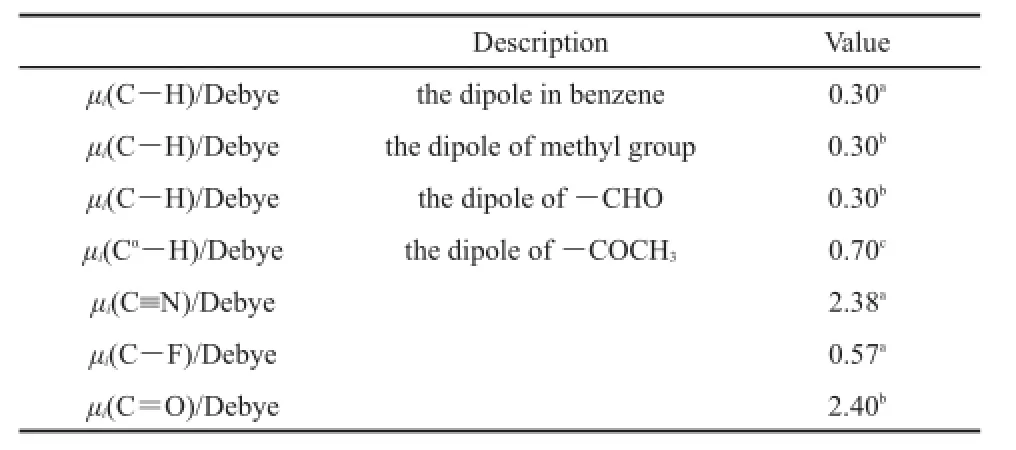
Table 1 Parameters for bond dipole moments used in this work

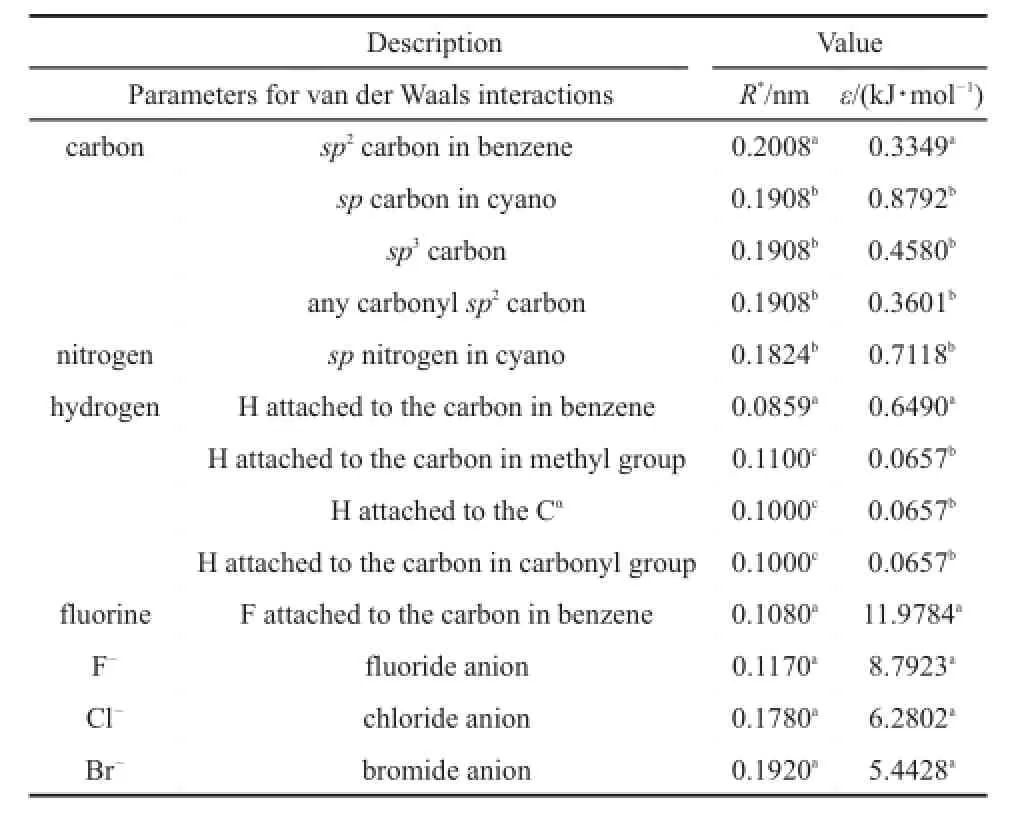
Table 2 Parameters for van der Waals used in this work

In Tables 1 and 239－41are collected the parameters μi,Rj*,Ra*,εjand εaobtained in this way.In Table 3 are listed the equilibrium intermolecular distances and interaction energies evaluated from Eq.(3)and from CCSD(T)/CBS.Table 3 indicates that our scheme produces the equilibrium intermolecular distances and interaction energies accurate enough as compared to the corresponding CCSD (T)/CBS results for all the training anion-π complexes.These comparisons show that the parameters determined here are reasonable.

3 Applications

Eq.(3)as well as the parameters μi,Rj*,Ra*,εjand εacollected in Tables 1 and 2 is employed in calculating the equilibrium intermolecular distances and interaction energies for fluoride,chloride, and bromide anion-containing complexes(Fig.3).In Table 4 are listed all the equilibrium intermolecular distances and interaction energies evaluated via our scheme and via the CCSD(T)/CBS method for these testing systems.Table 4 shows that the equilibrium intermolecular distances and interaction energies evaluated via our scheme agree well with the corresponding ones produced by the high-quality CCSD(T)/CBS method.As compared to the CCSD(T)/CBS intermolecular distances,our scheme displays an mean-unsigned deviation(MUD)of 0.004 nm and an RMSD of 0.004 nm.The maximum deviation is 0.009 nm found in the complex 16,the equilibrium intermolecular distance of which is predicted to be 0.249 nm by our scheme and 0.240 nm by the CCSD(T)/CBS method.As compared to the CCSD(T)/CBSinteraction energies,our scheme reproduces the high-quality CCSD(T)/CBS interaction energies satisfactorily for all twelve testing anion-π complexes.For instance,Table 4 indicates that the maximum absolute deviation is only 5.86 kJ·mol－1existed in thecomplex 16,the relative deviation of which is only 4.0%.Table 4 also indicates that the maximum relative deviation is 5.1% existed in the complex 18,the interaction energy(－107.98 kJ· mol－1)of the complex 18 evaluated via our scheme is very close to－102.83 kJ·mol－1produced via the CCSD(T)/CBS method. With respect to the CCSD(T)/CBS interaction energies,our scheme displays an MUD of 2.18 kJ·mol－1,an RMSD of 2.81 kJ· mol－1,and an MRD of 3.0%.Fig.4 shows that there exist favorable agreements between the potential energy curves produced via our scheme and produced via the high-quality CCSD(T)/CBS method. These comparisons manifest that our scheme can be used to accurately simulate anion－π interactions.

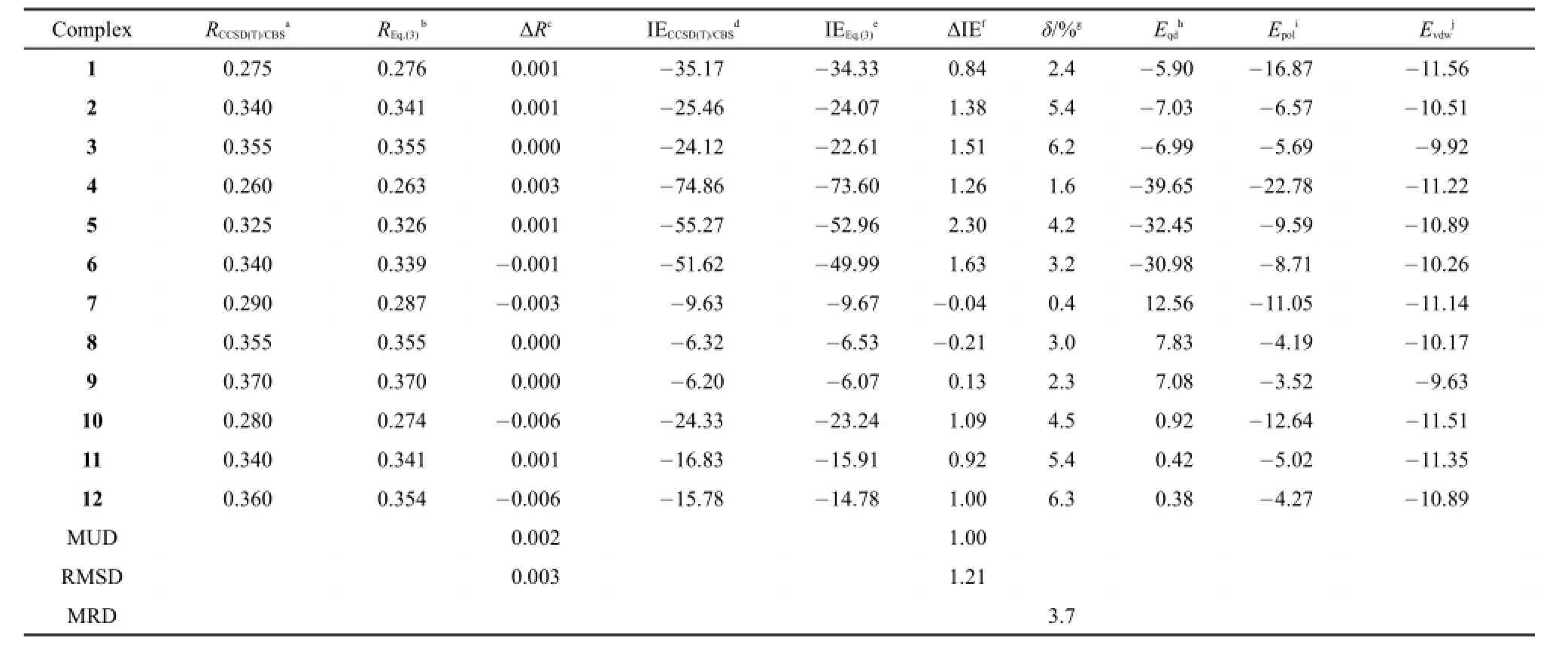
Table 3 Equilibrium intermolecular distances(nm)and interaction energies(kJ·mol－1)obtained from Eq.(3)and from CCSD(T)/CBS calculations for the training anion-π complexes

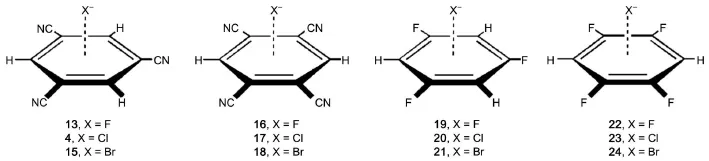
Fig.3 Testing anion-π complexes

Table 4 Equilibrium intermolecular distances(nm)and interaction energies(kJ·mol－1)obtained from Eq.(3)and from CCSD(T)/CBS calculations for the testing anion-π complexes

The interaction energy components,the electrostatic interaction Eqd,the polarization interaction Epol,and the van der Waals interaction Evdw,obtained from our scheme are also listed in Tables 3 and 4.It can be found by scrutinizing Tables 3 and 4 that the effect of substituents on the interaction strength mainly comes from the electrostatic interaction Eqd.For example,for the complexes 2,5, 14,and 17,in which one monomer is a chloride anion and another monomer is a benzene with one,two,three,and four cyano substituents,respectively,the equilibrium intermolecular distances for the complexes 2,5,14,and 17 are 0.341,0.326,0.316,and 0.309 nm predicted by Eq.(3),indicating that the more substituents,the shorter the distance between the two monomers.The intermolecular interaction energies for them were predicted to be－24.07,－52.96,－83.15,and－114.26 kJ·mol－1by Eq.(3),indicating that the more the substituents,the stronger the interaction between the two monomers.The interaction energy differences between the complexes 2 and 5,between the complexes 5 and 14, and between the complexes 14 and 17 are 28.9,30.2,and 31.1 kJ· mol－1,respectively.It can be found by scrutinizing the interaction energy components listed in Tables 3 and 4 that the electrostaticinteraction Eqdis－7.03,－32.45,－60.29,－89.51 kJ·mol－1for the complexes 2,5,14,and 17,respectively.The electrostatic interaction differences between the complexes 2 and 5,between the complexes 5 and 14,and between the complexes 14 and 17 are 25.4,27.8,and 29.2 kJ·mol－1.That is,the interaction energy difference between the complexes 2 and 5(28.9 kJ·mol－1)is almost the same as the electrostatic interaction difference between the complexes 2 and 5(25.4 kJ·mol－1),the interaction energy difference between the complexes 5 and 14(30.2 kJ·mol－1)is almost the same as the electrostatic interaction difference between the complexes 5 and 14(27.8 kJ·mol－1),and the interaction energy difference between the complexes 14 and 17(31.1 kJ·mol－1)is almost the same as the electrostatic interaction difference between the complexes 14 and 17(29.2 kJ·mol－1).Almost the same phenomenon can be observed for the complexes 8,11,20,and 23, in which one monomer is a chloride anion and another monomer is a benzene with one,two,three,and four fluorine substituents, respectively.

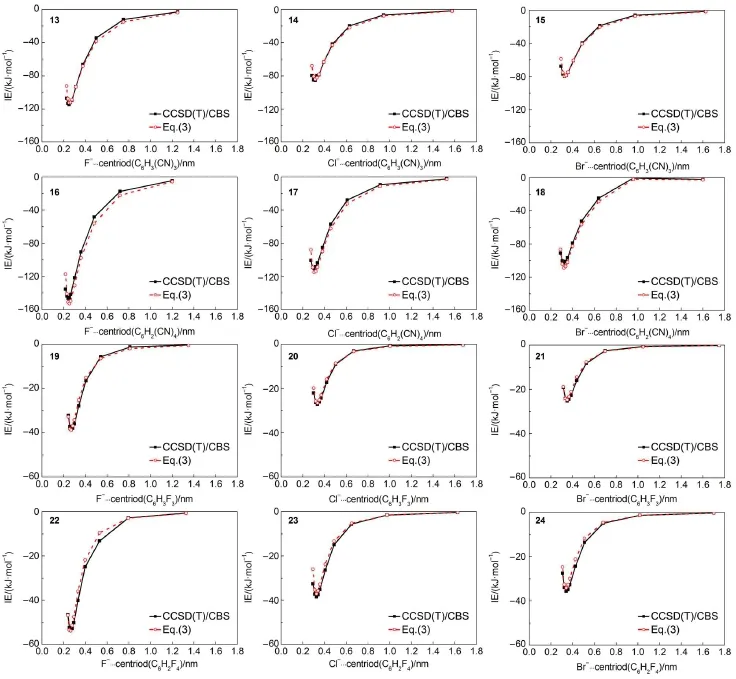
Fig.4 Potential energy curves obtained from CCSD(T)/CBS and from Eq.(3)for the testing 13－24 anion-π complexes

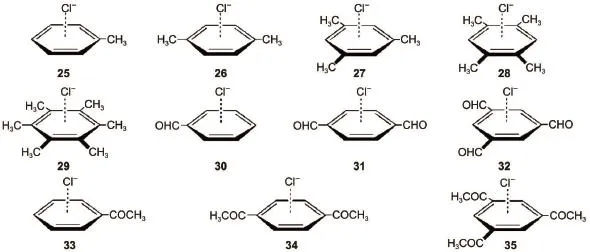
Fig.5 Testing anion-π complexes taken from Ref.29

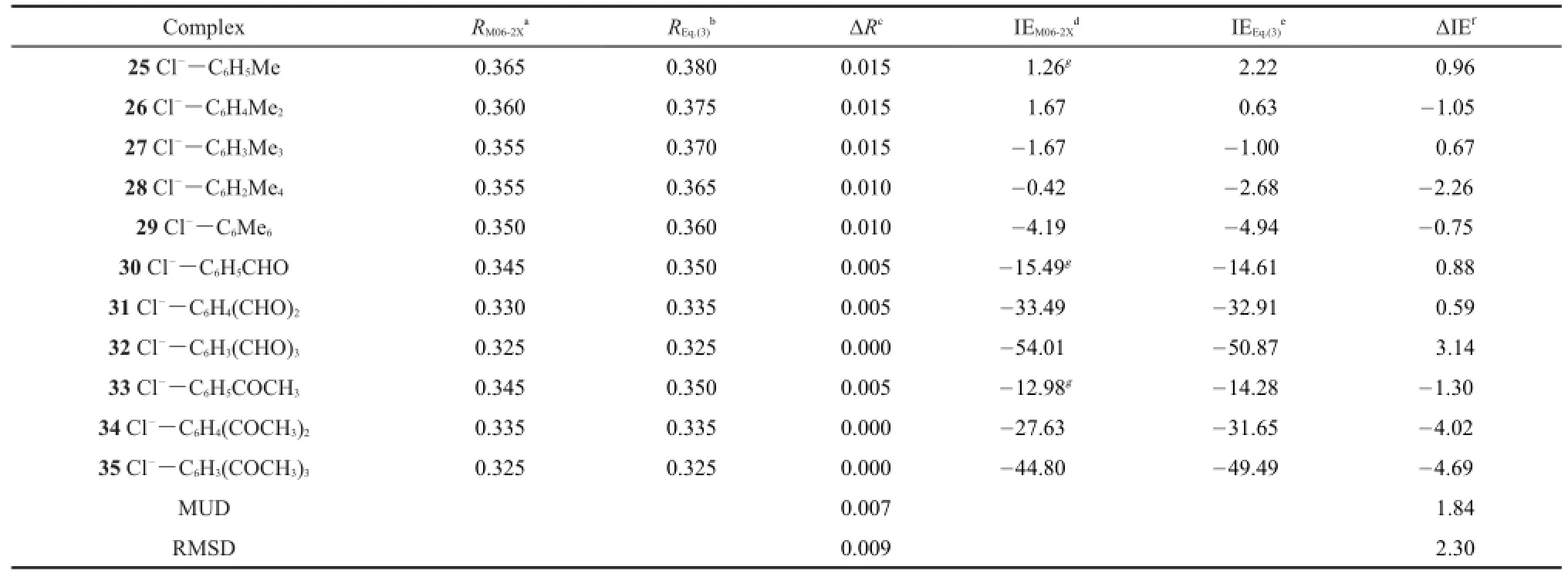
Table 5 Equilibrium intermolecular distances(nm)and interaction energies(kJ·mol－1)obtained from Eq.(3)and from M06-2X/6-31+G(d)calculations

It can also be found by scrutinizing Tables 3 and 4 that the effect of anion on the interaction strength comes from both the electrostatic interaction Eqdand the polarization Epolterms.That is, for a set of different anions binding to the same substituted benzene,the total interaction energy difference is almost equal to the difference of the summation of Eqdand Epol.For example,for the complexes 13 and 14,in which one monomer is a benzene with three cyano group and another monomer is fluoride anion or chloride anion,the interaction energy difference between the complexes 13 and 14 is 29.6 kJ·mol－1predicted by our scheme. The electrostatic interaction difference between them is 15.7 kJ· mol－1and the polarization interaction difference between them is 14.2 kJ·mol－1.That is,the difference(29.9 kJ·mol－1)of the summation of Eqdand Epolis almost the same as the difference (29.6 kJ·mol－1)of the interaction energy.Almost the same phenomena can be observed for the complexes 16 and 17,in which one monomer is a benzene with four cyano groups and another monomer is a fluoride anion or a chloride anion,and for thecomplexes 19 and 20,in which one monomer is a benzene with three fluorine substituents and another monomer is a fluoride anion or a chloride anion.

Eq.(3)is further applied to the anion-π systems as shown in Fig.5,which were proved to be important in the selective anion channels(especially chloride channel)and biological process29. The results obtained from Eq.(3)are listed in Table 5.In Table 5 are also given the results obtained by the M06-2X/6-31+G(d) method29.The data in Table 5 indicate that our scheme can produce accurate equilibrium intermolecular distances and interaction energies for these important complexes.

4 Conclusions

In this paper,a simple model,which explicitly contains electrostatic,polarization and van der Waals interactions,is proposed to rapidly simulate anion－π interactions and applied to systems composed of halide anion and substituted benzene.Our calculation results about the equilibrium intermolecular distances,interaction energies and potential energy curves produced by our scheme agree well with the corresponding ones produced by the highquality CCSD(T)/CBS method,demonstrating that the scheme proposed in this paper is accurate and efficient.Our calculation results show that the effect of substituents on the interaction strength mainly comes from the electrostatic interaction and the effect of anion on the interaction strength comes from both the electrostatic interaction and the polarization.Our calculation results show that our scheme can also be applied to anion-π systems important in the selective chloride channel.We anticipate the scheme proposed here could offer a helpful approach for efficiently and precisely simulating the anion－π interactions in biosystems.

(1) Meyer,E.A.;Castellano,R.K.;Diederich,F.Angew.Chem.Int. Ed.2003,42,1210.doi:10.1002/anie.200390319

(2) Salonen,L.M.;Ellermann,M.;Diederich,F.Angew.Chem.Int. Ed.2011,50,4808.doi:10.1002/anie.201007560

(3) Saberinasab,M.;Salehzadeh,S.;Solimannejad,M.Comp. Theor.Chem.2016,1092,41.doi:10.1016/j. comptc.2016.07.027

(4) Hunter,C.A.;Sanders,J.K.M.J.Am.Chem.Soc.1990,112, 5525.doi:10.1021/ja00170a016

(5) Desiraju,G.R.Angew.Chem.Int.Ed.Engl.1995,31,2311. doi:10.1002/anie.199523111

(6)Ebrahimi,A.;Masoodi,H.R.;Khorassani,M.H.;Ghaleno,M. H.Comp.Theor.Chem.2012,988,48.doi:10.1016/j. comptc.2012.02.027

(7) Berryman,O.B.;Bryantsev,V.S.;Stay,D.P.;Johnson,D.W.; Hay,B.P.J.Am.Chem.Soc.2007,129,48.doi:10.1021/ ja063460m

(8) Lee,E.C.;Kim,D.;Jurečka,P.;Tarakeshwar,P.;Hobza,P.; Kim,K.S.J.Phys.Chem.A 2007,111,3446.doi:10.1021/ jp068635t

(9)Wang,D.X.;Wang,M.X.J.Am.Chem.Soc.2013,135,892. doi:10.1021/ja310834w

(10) Fujisawa,K.;Beuchat,C.;Humbert-Droz,M.;Wilson,A.; Wesolowski,T.A.;Mareda,J.;Sakai,N.;Matile,S.Angew. Chem.Int.Ed.2014,53,11266.doi:10.1002/anie.201407161

(11) Bauzá,A.;Deyà,M.P.;Frontera,A.In Noncovalent Forces; Scheiner,S.Ed.;Springer International Publishing:Cham, 2015;pp 471－500.

(12) Cotelle,Y.;Benz,S.;Avestro,A.J.;Ward,T.R.;Sakai,N.; Matile,S.Angew.Chem.2016,128,4347.doi:10.1002/ ange.201600831

(13) Kim,K.S.;Tarakeshwar,P.;Lee,J.Y.Chem.Rev.2000,100, 4145.doi:10.1021/cr990051i

(14) Mooibroek,T.J.;Black,C.A.;Gamez,P.;Reedijk,J.Cryst. Growth Des.2008,8,1082.doi:10.1021/cg7009435

(15) Riley,K.E.;Pitoňák,M.;Jurečka,P.;Hobza,P.Chem.Rev. 2010,110,5023.doi:10.1021/cr1000173

(16) Hoog,P.D.;Gameɀ,P.;Mutikainen,I.;Turpeinen,U.;Reedijk, J.Angew.Chem.Int.Ed.2004,43,5815.doi:10.1002/ anie.200460486

(17) Rosokha,Y.S.;Lindeman,S.V.;Rosokha,S.V.;Kochi,J.K. Angew.Chem.Int.Ed.2004,43,4650.doi:10.1002/ anie.200460337

(18) Zhang,D.;Chatelet,B.;Serrano,E.;Perraud,O.;Dutasta,J.P.; Robert,V.;Martinez,A.Chem.Phys.Chem.2015,16,2931. doi:10.1002/cphc.201500610

(19) Alkorta,I.;Rozas,I.;Elguero,J.J.Am.Chem.Soc.2002,124, 8593.doi:10.1021/ja025693t

(20)Mascal,M.;Armstrong,A.;Bartberger,M.D.J.Am.Chem.Soc. 2002,124,6274.doi:10.1021/ja017449s

(21) Quiñonero,D.;Garau,C.;Frontera,A.;Ballester,P.;Costa,A.; Deyà,P.M.Chem.Phys.Lett.2002,359,486.doi:10.1016/ S0009-2614(02)00709-1

(22) Quiñonero,D.;Garau,C.;Rotger,C.;Frontera,A.;Ballester,P.; Costa,A.;Deyà,P.M.Angew.Chem.Int.Ed.2002,41,3389. doi:10.1002/1521-3773(20020916)41:18〈3389::AIDANIE3389＞3.0.CO;2-S

(23) Schottel,B.L.;Chifotides,H.T.;Shatruk,M.;Chouai,A.; Pérez,L.M.;Bacsa,J.;Dunba,K.R.J.Am.Chem.Soc.2006, 128,5895.doi:10.1021/ja0606273

(24)Dawson,R.E.;Hennig,A.;Weimann,D.P.;Emery,D.; Ravikumar,V.;Montenegro,J.;Takeuchi,T.;Gabutti,S.; Mayor,M.;Mareda,J.;Schalley,C.A.;Matile,S.Nat.Chem. 2010,2,533.doi:10.1038/nchem.657

(25)Giese,M.;Albrecht,M.;Rissanen,K.Chem.Commun.2016, 52,1778.doi:10.1039/C5CC09072E

(26)Kim,D.;Tarakeshwar,P.;Kim,K.S.J.Phys.Chem.A 2004, 108,1250.doi:10.1021/jp037631a

(27) Quiñonero,D.;Garau,C.;Frontera,A.;Ballester,P.;Costa,A.; Deyà,P.M.J.Phys.Chem.A 2005,109,4632.doi:10.1021/jp044616c

(28) Lucas,X.;Frontera,A.;Quiñonero,D.;Deyà,P.M.J.Phys. Chem.A 2010,114,1926.doi:10.1021/jp9089672

(29) Wheeler,S.E.;Houk,K.N.J.Phys.Chem.A 2010,114,8658. doi:10.1021/jp1010549

(30) Carrazana-García,J.A.;Rodríguez-Otero,J.;Cabaleiro-Lago, E.M.J.Phys.Chem.B 2012,116,5860.doi:10.1021/jp302271y

(31) Garau,C.;Quiñonero,D.;Frontera,A.;Ballester,P.;Costa,A.; Deyà,P.M.J.Phys.Chem.A 2005,109,9341.doi:10.1021/ jp053380p

(32) Frontera,A.;Quiñonero,D.;Costa,A.;Ballester,P.;Deyà,P.M. New J.Chem.2007,31,556.doi:10.1039/b612848c

(33) Helgaker,T.;Jorgensen,P.;Olsen,J.Molecular Electronic-Structure Theory;Wiley:New York,2000.

(34) Halkier,A.;Helgaker,T.;Jørgensen,P.;Klopper,W.;Olsen,J. Chem.Phys.Lett.1999,302,437.doi:10.1016/S0009-2614(99) 00179-7

(35) Řezáč,J.;Riley,K.E.;Hobza,P.J.Chem.Theory Comput. 2011,7,2427.doi:10.1021/ct2002946

(36) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 09, Revision D.01;Gaussian Inc.:Wallingford,CT,USA,2009.

(37) Garau,C.;Quiñonero,D.;Frontera,A.;Ballester,P.;Costa,A.; Deya,P.M.New J.Chem.2003,27,211.doi:10.1039/ B210110F

(38)Buckingham,A.D.;Fowler,P.W.;Hutson,J.M.Chem.Rev. 1988,88,963.doi:10.1021/cr00088a008

(39) John,A.D.Lange′s Handbook of Chemistry,5th ed.;McGraw-Hill Inc.:New York,1998.

(40) Li,S.S.;Huang,C.Y.;Hao,J,J.;Wang,C.S.J.Comput.Chem. 2014,35,415.doi:10.1002/jcc.23473

(41) Cornell,W.D.;Cieplak,P.;Bayly,C.I.;Gould,I.R.;Kenneth M.;Merz,J.;Ferguson,D.M.;Spellmeyer,D.C.;Fox,T.; Caldwell,J.W.;Kollman,P.A.J.Am.Chem.Soc.1995,117, 5179.doi:10.1021/ja00124a002

A Scheme for Rapid Simulation of Anion－π Interactions Involving Halide Anions and Substituted Benzenes

WANG Xiao-Wen LI Lei WANG Chang-Sheng*
(School of Chemistry and Chemical Engineering,Liaoning Normal University,Dalian 116029,Liaoning Province,P.R.China)

A scheme that explicitly contains electrostatic,polarization,and dispersion interactions to rapidly simulate anion－π interactions is proposed and assessed by structural and energetic comparison with those produced via the complete basis set limit of the coupled-cluster singles and doubles plus perturbative triples [CCSD(T)/CBS]method for a set of X－…C6H6－nRncomplexes where X－=F－,Cl－,Br－and R=CN,F.We use the chemical bonds C≡N,C―F,and C―H of the substituted benzenes as bond dipoles.The electrostatic interactions are estimated by calculating the interactions between the charge of the anion and the bond dipole moments of the substituted benzene.The polarization interactions are described according to the variation of the magnitudes of the bond dipole moments with the local environment.The parameters needed are produced by fitting the high-quality CCSD(T)/CBS potential energy curves.Calculation results show that our scheme produces equilibrium intermolecular distances with a root-mean-square deviation of 0.004 nm and interaction energies with a root-mean-square deviation of 2.81 kJ·mol－1compared with the CCSD(T)/CBS results.The calculation results also show that our scheme reproduces the CCSD(T)/CBS potential energy curves well.These comparisons indicate the scheme proposed here is accurate and efficient,suggesting it may be a helpful tool to design and simulate relevant molecular materials.

Anion－π interaction;Electrostatic interaction;Polarization;Bond dipole moment; Interaction energy

O641

10.3866/PKU.WHXB201612292

Received:November 2,2016;Revised:December 28,2016;Published online:December 29,2016.

*Corresponding author.Email:chwangcs@lnnu.edu.cn;Tel:+86-411-82156801.

The project was supported by the National Natural Science Foundation of China(21173109,21573098).国家自然科学基金(21173109,21573098)资助