基于修正变分法开孔板和加强板结构的自由振动分析

袁国清+俞瑜+王宗龙+李宁+蔡佑林+孙驰

摘要： 为研究船舶开孔板和加强板结构的振动特性，用1阶剪切变形板理论描述各向同性板的位移场，并采用修正变分原理和区域分解方法建立板的离散动力学模型.每一块子域板的位移和转角分量通过第一类切比雪夫正交多项式展开.针对加强板模型，将该方法获得的结果与已经发表的文献和有限元商用软件计算结果进行对比，验证该方法的收敛性和正确性.基于修正变分法探讨多种开孔和加强板模型的自由振动特性，充分说明该数理模型和半解析方法是一种适合处理复杂板结构问题的数值工具.

关键词： 船舶； 开孔板； 加强板； 自由振动； 修正变分法； 1阶剪切变形板理论； 区域分解方法； 第一类切比雪夫正交多项式

中图分类号： TB123文献标志码： B

Abstract： To study the vibration characteristics of structures of plates with hole and reinforcement plates in ships， the firstorder shear deformable plate theory is used to describe the displacement fields of isotropic plates， and a discretized dynamics model is built for a plate by a modified variational principle combined with multisegment partitioning procedure. The displacement and rotation components of each plate segment are expanded by Chebyshev orthogonal polynomials of first kind. As to the reinforcement plate model， the results obtained by the method are compared with the data in published references and the results calculated by commercial finite element software， and the convergence and accuracy of this method are validated. Based on the modified variational method， the free vibration characteristics of various plate with holes and reinforcement plates are discussed. The results indicate that the mathematical model and the semianalytical method may be used as appropriate numerical tools in the analysis and design of complicated plate structures.

Key words： ship； plate with hole； reinforcement plate； free vibration； modified variational method； firstorder shear deformable plate theory； multisegment partitioning procedure； Chebyshev orthogonal polynomials of first kind

0引言

在船體结构设计中，开孔和加强筋对板结构振动特性的影响是经常遇到的关键问题.根据船体总装的需求，开孔板主要有矩形、圆形和椭圆形开孔板，加强板有加筋板、T型板和交叉板等.虽然可以采用许多不同的数值方法建立板结构动力学模型，比如有限差分法、有限元法和边界元法等，但是寻找一种解析方法更有利于参数化研究、灵敏度分析和优化设计，比如线缆和管道布置需要的开孔位置发生变化通常会导致板振动特性发生显著变化.解析方法能通过位置参数的优化方便地获得合适的开孔位置，而数值算法需要一系列反复的重新建模、网格划分和计算.

LEE等[1]基于应力变形板理论和Timoshenko梁理论，采用有限元法研究各向异性板考虑偏心加筋的振动特征问题.LIEW等[2]采用RayleighRitz法建立矩形Mindlin加筋板的动力方程，并研究筋的剪切变形、转动惯量和扭转刚度的影响.WANG等[3]为获得开孔板最大基本振动频率，采用Ritz法对开孔位置进行优化.PEDERSEN[4]利用解析的方式描述椭圆开孔，并使用有限元分析和灵敏度分析对孔口形状和位置进行优化.QU等[5]为分析圆锥圆柱组合壳加环筋的振动特性，最早提出一种修正变分方法.YUAN等[6]通过分区广义变分原理，放松多板之间的界面以及几何边界的位移协调关系，处理多个加筋板组合的振动问题.本文基于1阶剪切变形板理论，将修正变分法进行拓展，推导开孔板和加强板结构二维区域划分的动力学公式，并将分析结果与已发表的实验结果和通过有限元软件计算的数值结果进行比较验证.板结构的动力学方程计算通过MATLAB编程实现.

1理论方法

1.1模型描述

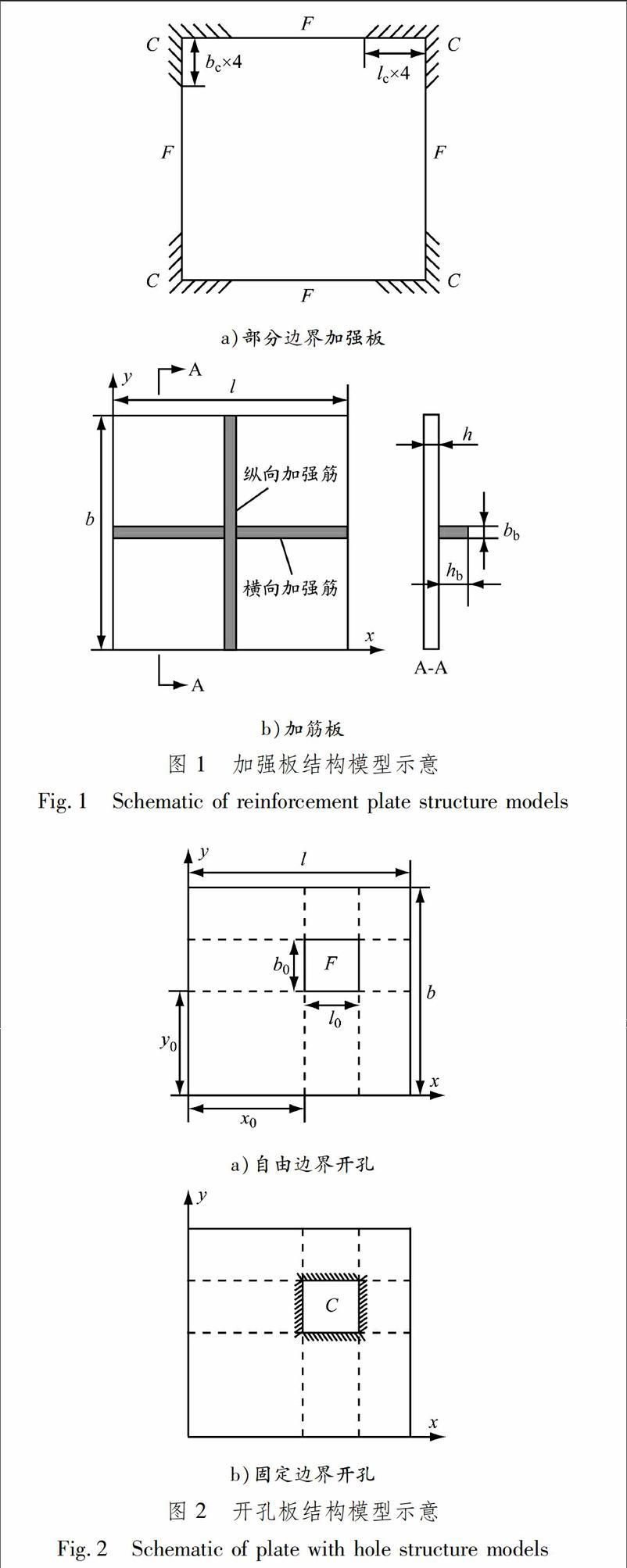
为不失一般性，选取几种加强和开孔板模型，见图1和2.加强板模型选取四边部分边界加强和筋条加强的模型；开孔模型选取矩形开孔，开孔边界分为自由和固定2种情形，自由边界是考虑通孔走线，固定边界是考虑在开孔处固定管道的情形.另外，开孔边界固定模型还能表征在平板表面局部加强的情形.

为简化计算，板和筋条的尺寸分别设置为固定值.笛卡尔系坐标（x，y，z）位于平板左下角.板的幾何尺寸为长l，宽b和厚h.部分边界固支位置为平板4个角，长边上为lc，宽边上为bc.所有的筋条横截面尺寸保持一致，即宽bb和厚度hb；矩形开孔的左下角位于（x0，y0），开孔为长l0和宽b0.假设所有的结构材料都是各向同性的，弹性模量E=2.1×1011 Pa，密度ρ=7 800 kg/m3和泊松比ν=0.3.平板模型振动分析考虑结构阻尼的影响，结构阻尼通过修改弹性模量来实现，即E=E0（1+iη），其中材料损失因子取η=0.006.

1.2修正变分方法

1.3动力学方程求解

从式（8）可以看出，通过修改变分原理和最小二乘加权余量法，分区界面连续性边界和几何边界条件得到释放和补偿.这就使得选取的位移函数不需要显性满足单个平板或者多板结构模型的原始边界条件.于是，各个平板子域的位移和转角函数只需要选取线性独立、完备的基函数就能获得数值准确解，这样可大大简化求解过程.在本章中，各个平板子域的位移和转角函数采用二维的第一类切比雪夫正交多项式展开[10]，表达式为

2仿真结果讨论

2.1加强板模型自由振动分析

在船舶设计中，一些板材需要调整结构来满足振动和应力方面的要求.加筋是最常见的增强板动力性能的方式，见图1b）加强板模型.为验证修正变分方法的可靠性和有效性，选取多种不同边界条件和多种加筋方式的加筋板自由振动数值仿真算例进行分析说明.在单个平板中定义其边界条件，例如用符号FSCF表示在平板的x=0，y=0，x=l和y=b边上分别是自由（F）、简支（S）、固定（C）和自由（F）边界条件.加筋板的几何尺寸为b=l=1 m，厚宽比为h/b=0.01，筋条宽、厚与平板厚度比值分别为bb/h=1和hb/h=1.5.加筋板的固有频率采用无量纲表示形式Ω=（ωb2/π2）ρh/D，其中D=Eh3/（12×（1-ν2））表示平板的弯曲刚度.基于前文中的公式推导，采用MATLAB编写程序并实现数值计算.计算获得的收敛解与采用RayleighRitz法计算的结果[2]进行对比.5种不同边界条件不同加筋方式的加筋板模型前6阶固有频率结果见表2.从表2中可以看出，本文方法与参考文献中的方法吻合很好.对于这5个算例，前6阶固有频率的最大相对误差小于2%，从而验证本文方法的精确性和有效性.

为进一步体现修正变分法的优越性，对局部边界加强板进行研究，模型见图1a）.定义边界条件lc=bc=l/5为固定，其余边界自由，可以发现这一模型可拓展到任意边界分布情形.基于本文方法和有限元软件ANSYS的计算结果见表3.对四边固支和局部固支模型的前6阶固有频率进行对比分析.为更好地理解加筋板的振动特性，给出局部边界固支板的前6阶固有频率结果和振型图见图3.表3中2个数值算例及2种方法计算结果吻合良好，最大相对误差为1.1%.

2.2开孔板模型自由振动分析

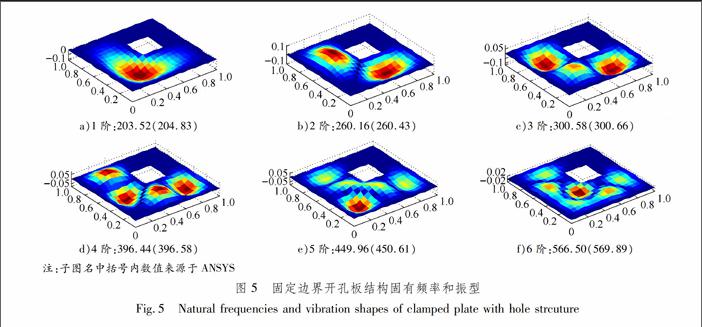
在船体管路和线缆分布设计中，通常需要在板材结构中打通孔，有时也会在开孔位置固定管材.为研究开孔对板结构振动特性的影响，研究矩形自由边界开孔和固定边界开孔2种情形，模型见图2.定义开孔尺寸和位置为b=l=1 m，h/b=0.01，x0/l=1/2，y0/b=1/2，l0/l=1/4，b0/b=1/4，平板四边为固支.自由边界开孔和固定边界开孔2种模型的前6阶固有频率见表5.将修正变分法和有限元法计算结果进行对比，2种方法计算结果最大误差为1.2%.固定边界开孔板的第1阶固有频率是自由开孔板的2倍多.对比表3中四边固定的平板结构前6阶固有频率，固定边界开孔比自由边界开孔对平板固有频率的影响更显著.自由边界开孔和固定边界开孔板的前6阶固有频率结果和振型图分别见图4和5.比较这2种开孔模型以及不开孔板模型的振型，同样是固定边界开孔板模型对振型的影响最显著.

基于开孔板模型的程序，多孔结构动力学方程只需将多个孔考虑成虚子域（即对应的子域质量矩阵和刚度为0）和开孔边界的组合，对于同样开孔尺寸的多孔板结构采用修正变分法进行振动分析非常方便快捷.另外，如果固定边界开孔的尺寸足够小，动力学方程就能仿真螺栓固定和点焊的情形.受限于篇幅，这样的模型不再一一列举.

3结论

基于1阶剪切变形板理论，采用修正变分法建立开孔和加强板结构的动力学模型.通过修改变分原理和最小二乘加权余量法，分区界面连续性边界和几何边界条件得到释放和补偿.这使得选取的位移函数不需要显性地满足单个平板或者多板结构模型的原始边界条件.局部边界加强模型仿真算例可推广到任意边界分布板问题.在处理离散加筋问题时，通过变分方法将筋条的动能和势能加载到动力方程中，加筋的位置参数用函数表示.开孔模型动力学方程将孔考虑成虚子域与开孔边界的组合，可应用于工程中常见的多孔板、螺栓固定和点焊等模型.基于修正变分法，各个平板子域的位移和转角函数采用切比雪夫多项式展开，可降低动力系统自由度，提高计算效率.通过与参考文献和有限元软件的仿真结果对比，验证修改变分方法的正确性和有效性.对于常见的板结构振动问题，本文中提到的数理模型和方法方便可行.

参考文献：

[1]LEE D M， LEE I. Vibration analysis of anisotropic plates with eccentric stiffeners[J]. Computers &structures， 1995， 57（1）： 99105.

[2]LIEW K M， XIANG Y， KITIPORNCHAI S， et al. Vibration of rectangular mindlin plates with intermediate stiffeners[J]. Journal of Vibration and Acoustics， 1994， 116（4）： 529535. DOI： 10.1115/1.2930459.

[3]WANG C M， WU W Q. Optimal location of a cutout in rectangular Mindlin plates for maximum fundamental frequency of vibration[J]. Structural and Multidisciplinary Optimization， 2002， 24（5）： 400404. DOI： 10.1007/s0015800202529.

[4]PEDERSEN N L. Optmization of holes in plates for control of eigenfrequencies[J]. Structural and Multidisciplinary Optimization， 2004， 28： 110. DOI： 10.1007/s0015800404268.

[5]QU Y G， CHEN Y， LONG X H， et al. A modified variational approach for vibration analysis of ringstiffened conicalcylindrical shell combinations[J]. European Journal of Mechanics A/Solids， 2013， 37： 200215. DOI： 10.1016/j.euromechsol.2012.06.006.

[6]YUAN G Q， JIANG W K. Vibration analysis of stiffened multiplate structure based on a modified variational principle[J]. Journal of Vibration and Control， 2015（1）： 115. DOI： 10.1177/1077546315621855.

[7]QU Y G， YUAN G Q， WU S H， et al. Threedimensional elasticity solution for vibration analysis of composite rectangular parallelepipeds[J]. European Journal of Mechanics A/Solids， 2013， 42： 376394. DOI： 10.1016/j.euromechsol.2013.07.006.

[8]QU Y G， LONG X H， WU S H， et al. A unified formulation for vibration analysis of composite laminated shells of revolution including shear deformation and rotary inertia[J]. Composite Structures， 2013， 98： 169191. DOI： 10.1016/j.compstruct.2012.11.001.

[9]QU Y G， CHEN Y， LONG X H， et al. Free and forced vibration analysis of uniform and stepped circular cylindrical shells using a domain decomposition method[J]. Applied Acoustics， 2013， 74（3）： 425439. DOI： 10.1016/j.apacoust.2012.09.002.

[10]JEFFERY A， DAI H H. Handbook of mathematical formulas and integrals[M]. 4th ed. San Francisco： Academic Press， 2008.（編辑武晓英）