航空发动机轮盘参数化结构优化
2017-05-12罗莉黄大永陈亚龙王克菲李杰
罗莉+黄大永+陈亚龙+王克菲+李杰
摘要: 为降低航空发动机轮盘的质量,提高发动机推质比,对发动机转子轮盘进行参数化结构优化设计.研究辐板不同高度处厚度与轮盘径向破裂裕度的关系,以简化轮盘辐板优化方法.以周向破裂转速裕度为约束条件,体积最小为优化目标函数,利用Isight软件和有限元数值模拟方法研究轮盘盘心优化方法,并通过算例计算验证其正确性.结果表明:在满足約束条件的基础上,轮盘体积减小8.66%,最大等效应力减少10.4%.该方法可为航空发动机轮盘轻量化开发提供参考.
关键词: 航空发动机; 轮盘; 辐板厚度; 破裂裕度; 破裂转速; 等效应力; 约束; 体积
中图分类号: V232.4文献标志码: B
Abstract: To reduce the aeroengine disk mass and improve the thrust to weight ratio of engine, the parameterized structural optimization is performed on an engine rotor disk. The optimization method of disk web is simplified by researching the relation between web thickness in different heights and radial burst margin of disk. Taking circumferential burst speed margin as the constraint condition and minimum volume as optimization objective function, Isight software and finite element analysis simulation is used to study disk center optimization method, and an example is calculated to verify its correctness. The results show that, on the basis of satisfying constraint condition, the disk volume is reduced by 8.66% and the maximum equivalent stress is reduced by 10.4%. The method can provide reference for the lightweight development of aeroengine turbine disk.
Key words: aeroengine; turbine disk; web thickness; burst margin; burst speed; equivalent stress; constraint; volume
0引言
轮盘是航空发动机重要的安全关键件之一,在高转速、高温度、高压力的恶劣条件下工作.轮盘的转速一般都达到每分钟数千转到数万转,负责固定叶片的轮盘除要承受自身的离心力外还要承受叶片的巨大离心载荷.由于叶片和轮盘的离心载荷很大,需要较大的盘心承受,所以轮盘设计得比较重.以高压涡轮为例,其单盘的质量能占到整个高压涡轮部件总质量的50%.由于涡轮盘质量巨大,其一旦破坏,产生的高能碎块是任何机匣都无法包容的,因此为保证涡轮盘的可靠性,其设计也不得不保守.随着优化技术的发展以及市场对产品效率的要求越来越高,对轮盘的轻质化设计需求也越强烈.早期国内有开展整体叶盘的设计研究[13],随着焊接技术和材料研究的发展[45],轻质化轮盘的优化方法又有双辐板轮盘设计的研究方向[69],但国内实际工程应用,依然是单辐板为主要设计形式.榫槽形状的优化也是轮盘优化的一种有效途径[10].考虑到多辐板涡轮盘的加工制造存在较高的技术要求,基于国内现有的成熟加工能力,本文从工程应用的角度考虑,对分体盘盘体寻求一种简洁、高效的优化设计方法.
1轮盘结构优化设计思路
轮盘破裂对发动机的破坏程度极其严重,而且是非包容性的.为防止轮盘破裂,轮盘的优化设计以轮盘的破裂转速储备裕度为限制条件.对于高速旋转的轮盘而言,径向破裂裕度和周向破裂裕度是轮盘安全性的2个重要指标.
径向破裂裕度最薄弱的区域为辐板,因此当轮盘的径向破裂转速有一定的裕度时,可以适当减薄辐板位置的厚度,通过降低径向破裂转速的裕度达到减重的目的.根据周向破裂裕度的计算方法[1112]可知盘心和辐板为周向破裂裕度的计算区域,而盘心是承载周向载荷的重要区域,因此,对轮盘的优化考虑采取2步:第一步对辐板优化,第二步对盘心优化.
以轮盘的破裂裕度为约束条件,优化轮盘设计.破裂转速的计算方法采用常用的平均应力法和有限元方法.破裂转速储备裕度的计算公式[1112]为Mburst=mσUTSσAVGTan式中:m为材料利用系数;σUTS为平均工作温度下的材料强度极限;σAVGTan为平均周向应力或平均径向应力.
2轮盘辐板优化
2.1幅板各高度处厚度变化交互影响研究
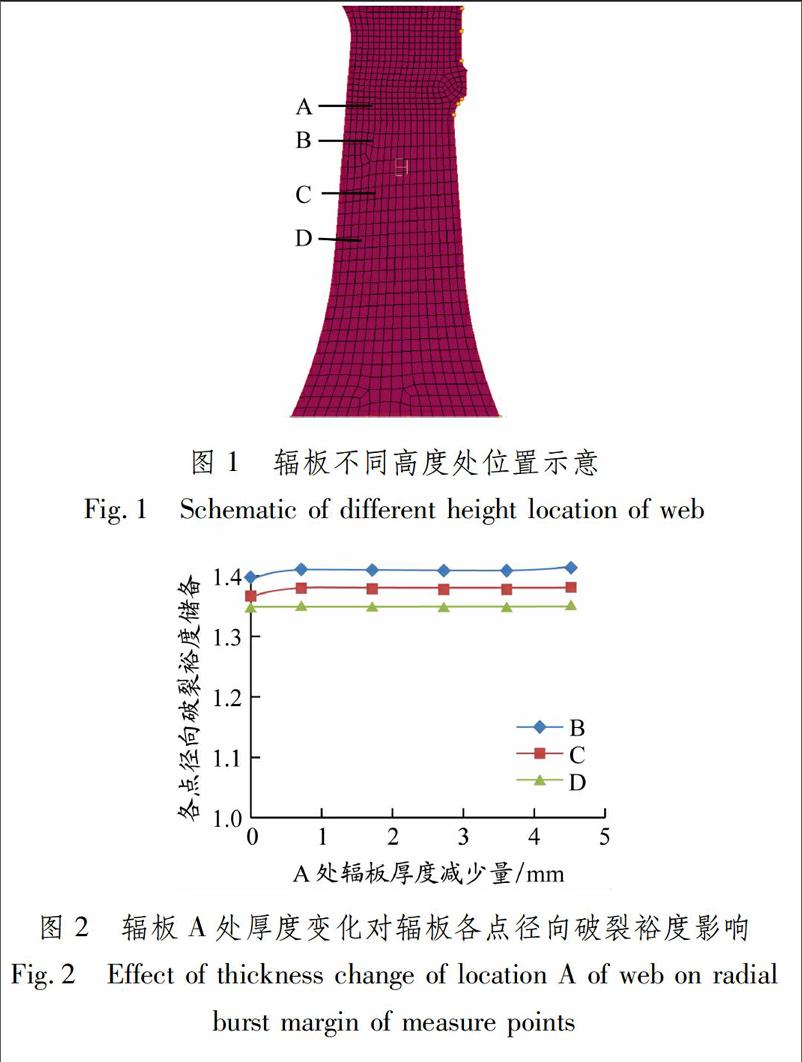
辐板的径向载荷主要由喉部以上结构的离心力产生,辐板自重对辐板的径向载荷影响较小,假定辐板某个高度处的厚度只对此高度处的径向破裂储备有影响,由于厚度变化而导致的离心载荷变化可以忽略,辐板各高度处的厚度对其他高度处的平均径向应力的影响可以忽略不计,幅板各高度处厚度变化无交互影响.轮盘辐板的A~D位置见图1,通过HyperMesh的Morph功能,逐渐减少辐板高度A处的厚度,计算轮盘辐板B,C和D处的径向破裂裕度,见图2.从图2可以看出,轮盘高度A处的厚度变化对B,C,D处的径向破裂储备影响非常小,因此可以认为对于径向破裂裕度,幅板A高度处厚度变化对B,C,D高度处无交互影响.
2.2辐板厚度变化与径向破裂裕度的关系
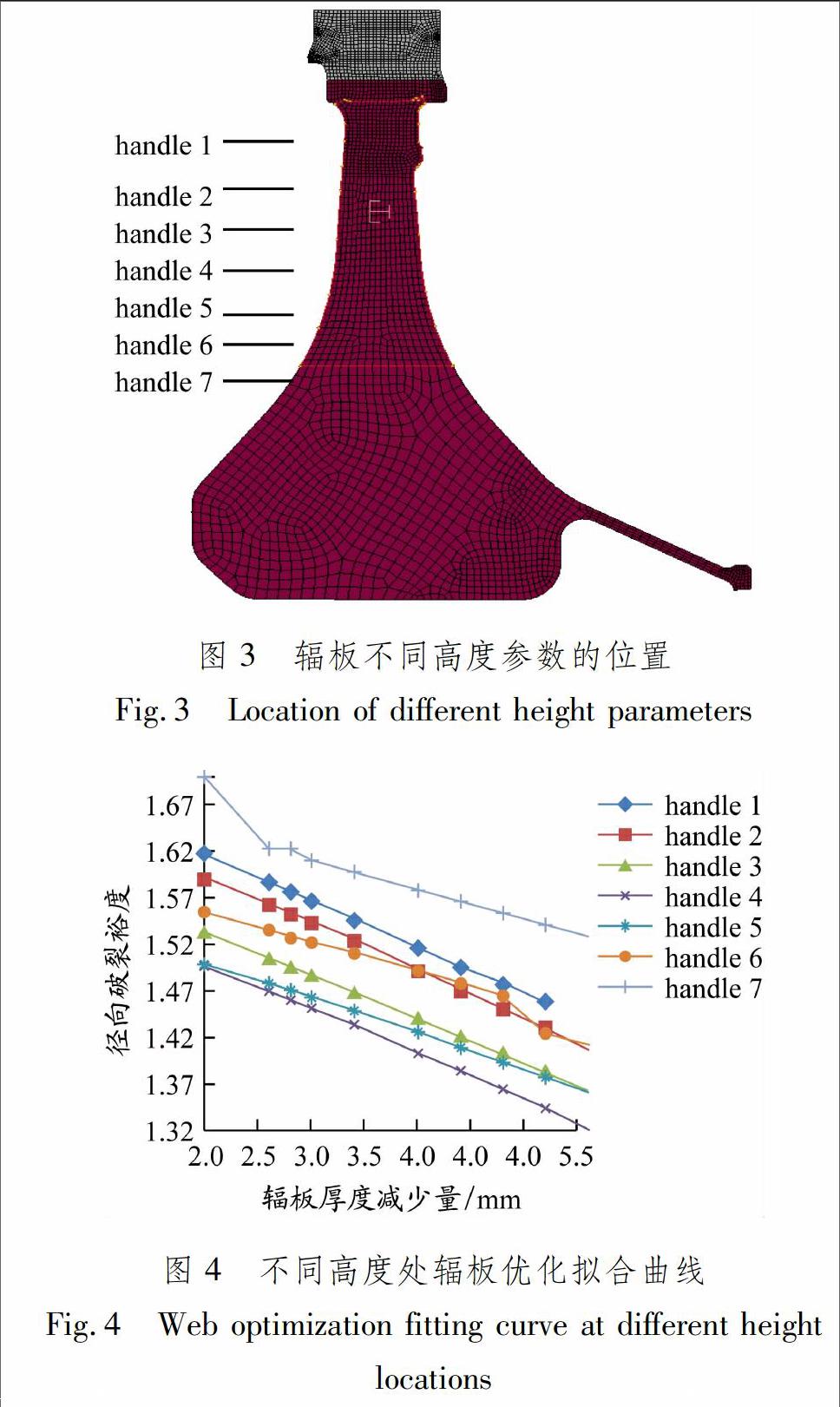
在轮盘的辐板上选取不同高度为handle 1,handle 2,handle 3,handle 4,handle,5和handle6 等多处截面,见图3.以每个截面高度处的辐板厚度为参变量,计算每个截面高度不同厚度的径向破裂转速储备.以辐板厚度的减少量为横坐标,徑向破裂裕度为纵坐标绘制曲线,可以得到各处辐板厚度减少值与对应高度的径向破裂裕度关系.进而拟合辐板优化的曲线见图4.
由图4可知,在辐板区域范围,对应高度处的厚度变化与径向破裂裕度近似成线性关系为f(x)=ax+b (1)在辐板喉部,厚度参数变化与径向破裂裕度的线性关系匹配度较高;在接近盘心的部位,厚度参数变化与径向破裂裕度的拟合曲线为多段折线线性关系,例如handle 7处的辐板优化拟合曲线不再是一条直线.然而,轮盘的最小径向破裂裕度发生的位置是辐板的喉部位置,这个位置的辐板厚度最小,因此轮盘辐板的优化可以采用线性公式.
2.3辐板优化算例
以某轮盘为算例,辐板优化步骤如下.
(1)基于HyperMesh网格模型,开展参数化建模.该方法在网格变化的同时,温度场随之变化,可减少温度场的反复迭代和反复分网过程.
(2)研究辐板厚度变化与径向破裂裕度的关系,获取优化拟合曲线.
(3)基于ANSYS环境进行有限元计算和后处理分析.
优化设计流程见图5.对轮盘原设计结构进行有限元建模,采用带中节点的四边形单元SOLID183.模型中的几何形状和载荷条件满足轴对称条件的位置采用轴对称单元,榫接位置采用带厚度的平面应力单元.边界条件约束辐板右侧,见图6.轮盘温度分布范围为450~500 ℃,呈径向梯度分布,见图7.转子叶片位置采用质量单元MASS21模拟叶片离心力.
轮盘的材料为FGH96合金[13],密度ρ=8.32×103 kg/m3,泊松比为0.311.
在轮盘辐板不同高度位置,通过改变各位置的参数值,计算轮盘的各点平均径向应力与径向破裂裕度.根据辐板优化的拟合方程,获取各高度处a和b的值,见表1.
径向破裂储备目标设为1.4,通过辐板优化的拟合方程,可以获得辐板各高度处的可减少厚度值.优化后的辐板模型见图8.
优化后辐板的最大等效应力水平相当,应力分布趋势相似,见图9和10.轮盘辐板优化前后的计算结果见表2.
优化后的轮盘体积减少6.77%,径向破裂裕度由1.540减少到1.400,满足优化设计约束条件.优化后,轮盘的周向破裂裕度未明显变化,与原始模型的周向破裂裕度相当.
3轮盘盘心优化
轮盘盘心是轮盘周向破裂裕度影响的重要因素.盘心优化流程见图11.
以盘心不同高度位置的厚度为参数,建立有限元模型.通过试验设计方法确定参数取值和样本点,变化盘心的几何形状进行仿真计算.以盘心的体积为优化目标,以盘心的周向破裂裕度为约束条件;通过Isight软件中的优化算法分析计算结果,获取优化的参数值;最后以优化参数值建立模型,完成有限元求解,验证优化参数的正确性.
4盘心优化算例
在优化后辐板模型的基础上开展盘心优化,以盘心厚度为参变量,见图12.参数P1~P6变化范围为-5~+5 mm,以周向破裂裕度大于1.297为限制条件,以体积最小值为优化目标.
通过试验设计确定样本点的值,采用HyperMesh的Morph功能生成有限元模型,完成各样本的有限元计算.根据各样本点有限元计算结果,在Isight软件中获取输入变量与输出变量的相关性.各变量对破裂裕度和体积的影响分别见图13和14.由此可以看出:P3对优化目标体积和约束条件破裂裕度影响比重都较大.在要保证约束条件的情况下减小体积,需要选择对约束条件不敏感、对优化目标影响大的参数,进行较大调整.
为较精确地找到全局最优点,采用多岛遗传算法[1415].多岛遗传算法是在传统遗传算法的基础上,基于群体分组的并行性遗传算法.多岛遗传算法将整体种群划分为若干子群,并将子群隔绝于不同的“岛屿”上,各个子群独立地进化,而非全部种群采用相同的进化机制,并且各个“岛屿”间以一定的时间间隔进行“迁移”,使各个“岛屿”间进行信息交换.多岛遗传算法能够有效地提高运算速度,并且若干独立进化的子群可提高整个种群的遗传多样性,回避传统遗传算法的早熟现象,有利于找到全局最优解.
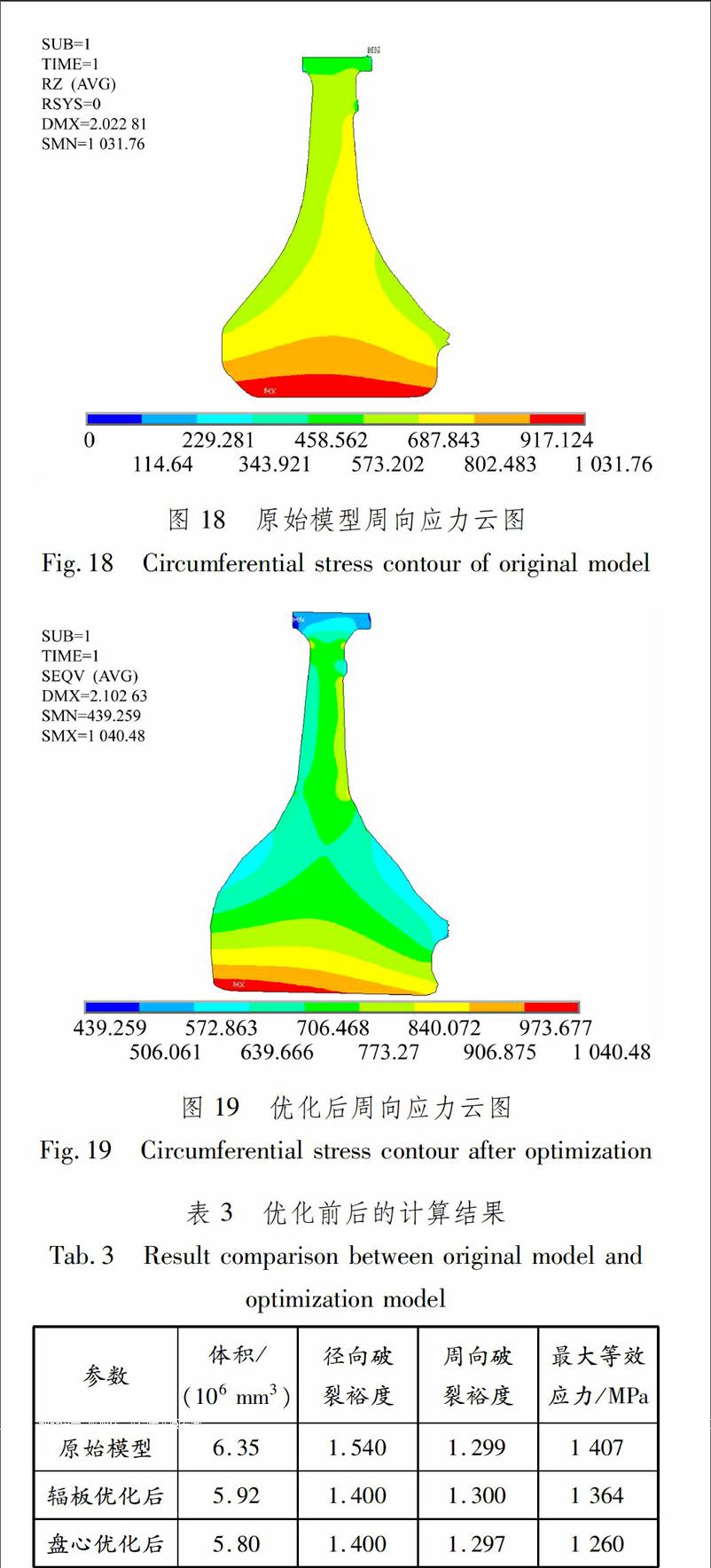
通过多岛遗传优化算法,获取各变量的取值,建立盘心优化后的有限元模型.原始模型与优化完成后的模型对比见图15.模型优化前、后的应力云图对比见图16~19,计算结见表3.与原始模型相比,优化后模型的最大等效应力减少.由图18和19可知,优化前后方案轮盘周向破裂最大应力均发生在盘心位置.由图19和表3可知,优化后的轮盘最大周向应力为1 040 MPa,增加0.7%,周向破裂裕度满足大于1.297的约束条件.优化后的轮盘质量减少8.66%,径向破裂裕度由1.540减少到1.400,周向破裂裕度由1.299减少到1.297,满足约束条件.
由表3可知,盘心优化后模型的径向破裂裕度与辐板优化后模型的结果相同,均为1.400,盘心的形状改变未影响轮盘的径向破裂裕度,因此轮盘分步骤开展优化工作可行并高效.
5结论
本文以轮盘为研究对象,以轮盘厚度为参变量、破裂裕度为优化限制条件、体积为优化目标,研究轮盘的优化设计方法,得到以下结论.
(1)对轮盘的优化可以采用辐板和盘心优化分步开展的方法,以减少优化参变量的个数和类型.本文仅选择厚度作为变量,优化方法高效、简单.
(2)幅板各高度处厚度变化对其他高度处的径向破裂裕度无明显交互影响.
(3)辐板的减重优化可按照线性拟合曲线,有利于简单、高效完成辐板优化设计,具有一定通用性.
(4)辐板厚度的变化对轮盘的周向破裂裕度无明显影响.
(5)盘心的优化设计并未影响轮盘承担径向破裂载荷的能力.
(6)在满足设计目标的基础上,经过参数化优化,轮盘体积减小8.66%,最大等效应力减少10.4%.
该优化方法对轮盘的结构设计具有借鉴意义.后续工作可以在优化后模型的基础上,使轮盘的轮廓过度点更加平滑,减少局部的应力集中,消除几何角点的高应力区域.参考文献:
[1]陈光. 整体叶盘在国外航空发动机中的应用[J]. 航空发动机, 1999, 25(1): 16.
CHEN G. Application of whole blade disk in foreign aeroengine[J]. Aeroengine, 1999, 25(1): 16.
[2]黄春峰. 航空发动机整体叶盘结构及发展趋势[J]. 现代零部件, 2005, 3(4): 14. DOI: 10.16173/j.cnki.ame.2005.04.019.
HUANG C F. Structure of blisk and its growing trend[J]. Modern Components, 2005, 3(4): 14. DOI: 10.16173/j.cnki.ame.2005.04.019.
[3]姚利兵. 基于特征的整體叶盘CAD造型系统研究[D]. 西安: 西北工业大学, 2006.
[4]江和甫, 古远兴, 卿华. 航空发动机的新结构及其强度设计[J]. 燃气涡轮试验与研究, 2007, 20(5): 14.
JIANG H F, GU Y X, QING H. New structure and strength design of aeroengine[J]. Gas Turbine Experiment and Research, 2007, 20(5): 14.
[5]金捷, 钟燕. 先进航空发动机设计与制造技术综述[J]. 航空制造技术, 2012(5): 3437 DOI: 10.16080/j.issn1671833x.2012.05.017.
JING J, ZHONG Y. Design and manufacturing technology of advanced aeroengine[J]. Aeronautical Manufacturing Technology, 2012(5): 3437. DOI: 10.16080/j.issn1671833x.2012.05.017.
[6]王营, 余朝蓬. 航空发动机涡轮盘结构优化设计[J]. 机械设计与制造, 2010(5): 46.
WANG Y, YU Z P. Optimization design for turbine disk of a gas engine[J]. Machinery Design & Manufacture, 2010(5):46.
[7]陆山, 李伦未. 航空发动机高负荷涡轮盘双辐板结构优化设计[J]. 推进技术, 2011, 32(5): 631636, DOI: 10.13675/j.cnki.tjjs.2011.05.009.
LU S, LI L W. Twinweb structure optimization design for heavy duty turbine disk of aeroengine[J]. Journal of Propulsion Technology, 2011, 32(5): 631636. DOI: 10.13675/j.cnki.tjjs.2011.05.009.
[8]李伦未, 陆山. 基于ANSYS平台的多辐板风扇盘结构化设计技术[J]. 航空动力学报, 2011, 26(10): 22452250. DOI: 10.13675/j.cnki.tjjs.2011.05.009.
LI L W, LU S. Structure optimization design techniques for multiweb fan disk based on ANSYS platform[J]. Journal of Aerospace Power, 2011, 26(10): 22452250. DOI: 10.13675/j.cnki.tjjs.2011.05.009.
[9]张乘齐, 黄文周, 刘学伟, 等. 低惯量涡轮转子结构设计与优化[J]. 燃气涡轮试验与研究, 2013, 26(4): 3350.
ZHANG C Q, HUANG W Z, Liu X W, et al. Design and optimization of low inertia turbine rotor structure[J]. Gas Turbine Experiment and Research, 2013, 26(4): 3350.
[10]邢誉峰, 诸德超. 航空发动机涡轮盘榫槽的形状优化设计[J]. 航空学报, 1995(16): 14.
XING Y F, ZHU D C. Shape optimum design of engines turbodisk tenongrooves[J]. Acta Aeronautica et Astronautica Sinica, 1995(16): 14.
[11]冯引利, 吴长波, 高鹏, 等. 某粉末冶金高温合金涡轮盘破裂转速分析[J]. 航空动力学报, 2013, 28(3): 502506. DOI: 10.13224/j.cnki.jasp.2013.03.007.
FENG Y L, WU C B, GAO P, et al. Analysis of power metallurgy superalloy turbine discs burst speed[J]. Journal of Aerospace Power, 2013, 28(3): 502506. DOI: 10.13224/j.cnki.jasp.2013.03.007.
[12]吳长波, 卿华, 冯引利, 等. 某高压涡轮整体叶盘破裂转速计算方法及试验验证[J]. 燃气涡轮试验与研究, 2006, 19(8): 3336.
WU C B, QING H, FENG Y L, et al. Investigation on prediction and experiment of highpressure turbine blink burst speed[J]. Gas Turbine Experiment and Research, 2006, 19(8): 3336.
[13]中国金属学会高温材料分会. 中国高温合金手册[M]. 北京: 中国标准出版社, 2012.
[14]周明, 孙树栋. 遗传算法原理及应用[M]. 北京:国防工业出版社, 1999:4.
[15]牟淑志, 杜春江, 牟福元, 等. 基于多岛遗传算法的连续体结构拓扑优化[J]. 机械科学与技术, 2009, 28(10): 13161320. DOI: 10.13433/j.cnki.10038728.2009.10.010.
MU S Z, DU C J, MU F Y, et al. Topology optimization of a continuum structure using MultiIsland Genetic Algorithm(MIGA)[J]. Mechanical Science and Technology for Aerospace Engineering, 2009, 28(10): 13161320. DOI: 10.13433/j.cnki.10038728.2009.10.010.
