程序配电器减振器等效模拟及动强度分析

骆保民+樊新刚+董龙雷+杨宝琨

摘要： 为优化橡胶减振器与程序配电器的性能参数匹配，提高程序配电器的安全性和可靠性，在Patran中采用等效模拟的方法进行某橡胶减振器结构的有限元建模，分析连接螺栓的动态强度特性，并通过试验进行特性验证.结果证明所采用的建模方法和仿真技术可行.

关键词： 程序配电器； 橡胶减振器；模态分析； 动强度； 仿真； 试验

中图分类号： TP213文献标志码： B

Abstract： To optimize the performance parameters matching between program distributor and rubber damper and improve the security and reliability of the program distributor， the finite element model of a rubber damper structure is built using the method of equivalent simulation in Patran， the dynamic strength characteristics of connecting bolt is analyzed， and the characteristics are verified by test. The results show that the modeling method and the simulation technique are feasible.

Key words： program distributor； rubber damper； modal analysis； dynamic strength； simulation； test

0引言

程序配电器是航天运载器的重要结构，为保障其在强振动环境下正常工作且安全可靠，通常采用减振器装置降低其振动，并通过振动试验验证其动力学特性.[12]减振特性及结构强度是程序配电器结构设计最关注的问题.地面振动考核试验发现经常由于减振器参数设计不合理而造成结构发生动强度破坏.因此，本文从有限元分析角度出发，进行减振器结构设计参数研究并进行动强度分析[3].

以某型号运载器上安装的程序配电器为对象，使用有限元软件对其进行有限元建模和结构动力学分析.程序配电器减振器中使用的橡胶使其力学特性存在很强的非线性特征[4]，难以用现有的有限元软件精确地预测其性能，并且非线性分析计算量大，对计算机性能要求高.本文主要对关键部件的强度进行考核，尝试用直接瞬态响应的方法来研究问题.对薄弱环节采用等效静力的方法具体分析，可大大减少计算时间和存储要求，提高工作效率.

1模拟工作环境振动试验

某型号运载器上安装的程序配电器工作环境恶劣，由于结构并非完全对称，存在的不平衡因素可能造成减振器螺钉断裂等破坏情况.为保证仪器在使用环境下正常工作，进行工作环境的模拟振动试验.在低频段正弦扫频试验摸底试验（30～50 Hz，8.4g）循环中出现螺钉弯曲现象，所以有必要对程序配电器进行低量级振动试验分析.通过建立准确的有限元模型，分析螺钉出现弯曲现象的原因，对程序配电器的减振器结构设计提供理论支撑.

2动力学试验和分析

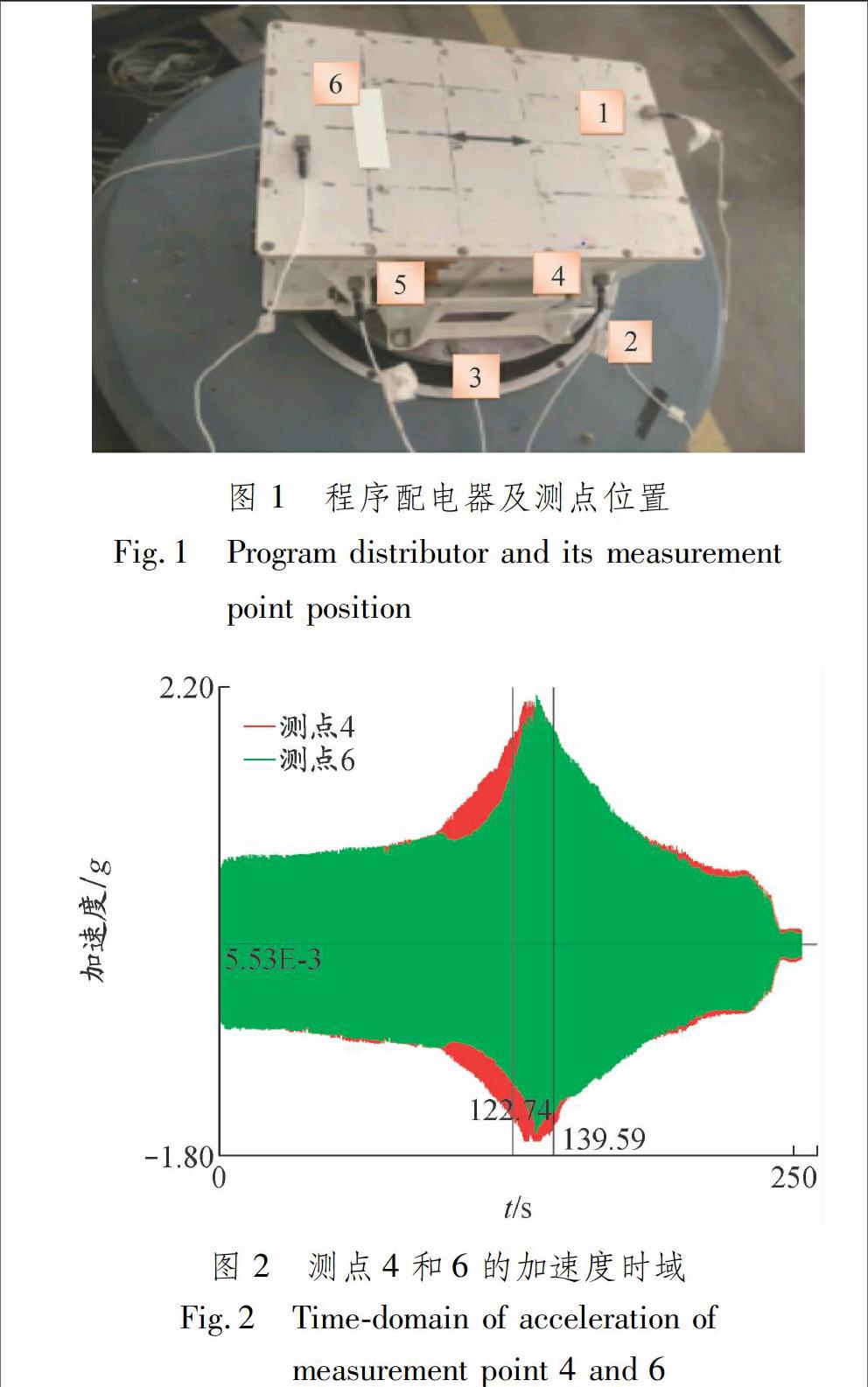
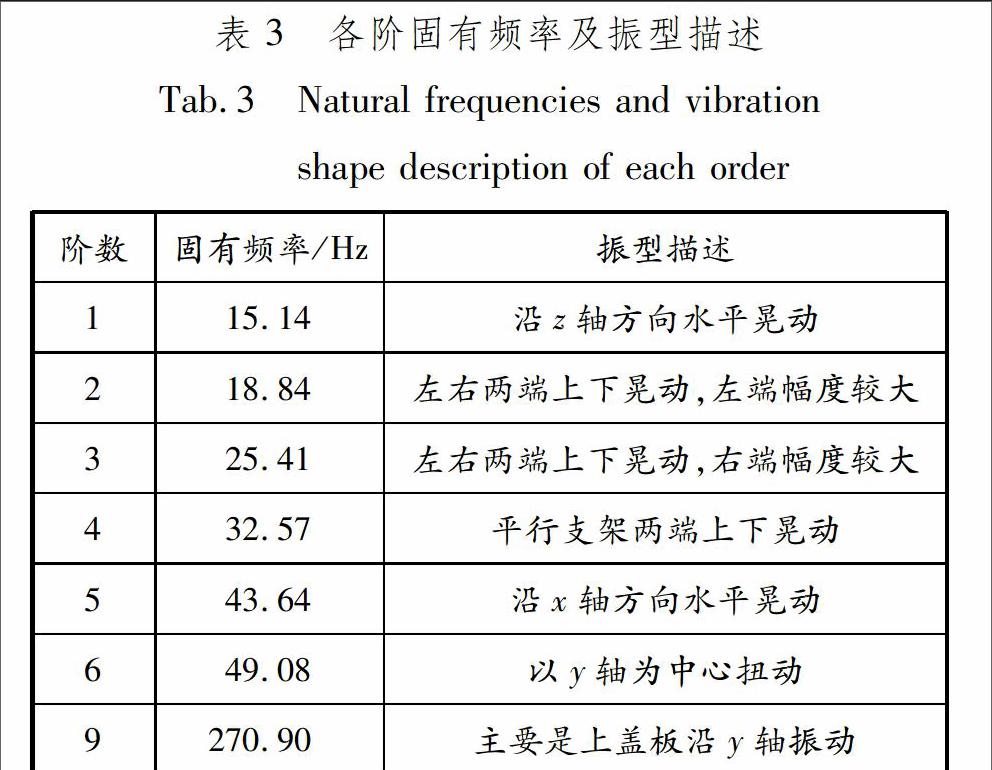
程序配电器及测点位置见图1.采用正弦扫频的激励方式进行低量级的振动试验.正弦扫频试验控制谱型为3～100 Hz内的谱线，正弦扫频的控制谱参数：3～8 Hz为4.5 mm，8～100 Hz为0.6g.测点4和6的z向响应时域图见图2，加速度最大值为1.8g～2.2g，放大了3～4倍.最大值出现在123～134 s内.

以测点3为激励点，对其他测点进行频响分析，结果见图3.通过曲线分析可知，在所关心的频率段内，频响函数毛刺比较多.测点2和参考点3都位于夹具上，2点的响应情况基本一致.z方向测点5和6在31.67 Hz附近出现峰值点，测点1，4，5和6在50 Hz附近出现多个峰值点.对程序配电器进行不同量级的振动试验测试，测点6的z方向频率响应函数对比见图4.由图4可知：随着激励的增大，固有频率有减小的趋势，较大振动量级的同一频段内峰值的个数会发生变化，可能在相同频率峰值数出现相邻振型互换的现象，反映出橡胶减震器的动刚度值随激励振幅增大而减小的规律，程序配电器表现出显著的非线性特征.

不同量级的振动对应不同的共振频率和动刚度，根据这一规律，通过试验的量级来选择仿真的刚度，对配电器进行预测.通过仿真分析，可选择合适的螺钉材料、改进结构设计，能够有效减少产品的破坏，减少试验次数，降低成本.

3程序配电器减振器等效建模

程序配电器结构主要包括3部分：箱体结构、减振器结构和支架结构.其中，箱体内部结构较为复杂，减振器结构的非线性显著，支架结构比较简单，因此，程序配电器的建模集中在箱体结构和减振器结构的处理上.

对于复杂结构，一次性导入所有零部件进行网格划分不仅困难而且容易丢失大量几何特征，所以为方便网格的划分和处理，采用组装导入的方式.为取得足够计算精度，整个结构采用实体建模，由于四面体单元刚度大，会影响计算精度，故严格控制四面体单元的个数，以六面体（CHEXA）单元为主划分有限元网格.程序配电器照片见图4，简化后的模型示意见图5.

3.1箱体结构有限元建模

在建立箱体几何模型时，忽略一些无关大局的螺栓孔、螺钉孔和过渡圆角，并对内部电路板的尺寸进行取整处理.这些简化处理使得大多数网格可以划分出精度较高的六面體单元，只有少部分的不规则单元，不会对整体模型的精度造成影响，所建立的几何模型除部分为不规则五面体外，其余均为六面体.由于结构大量采用螺钉连接，将机壳与上下盖以及电路板的固定使用等效节点直接看作整体，认为各部分之间没有相对运动.对箱体内部的电路板结构进行简化，采用实体单元建模，将内部电路板等效成钢板，通过调整钢板厚度使模型质量与设备实际质量基本保持一致.箱体结构的有限元模型见图6.

3.2箱体结构有限元模型的评价和修正

通过模态测试和试验结果分析，得到程序配电器箱体在弹性悬挂状态下各个方向的模态参数，建立其试验模型并验证有限元模型的有效性.为得到程序配电器箱体在自由状态下的模态参数，用柔性绳自由悬挂箱体，模拟自由状态下的边界条件，隔离环境振动干扰和排除基础的振动模态对试件模态的影响.箱体结构较重，所以不考虑传感器质量对整体结构的影响.

进行模态置信度计算，采用基于模态的相关性算法完成模态相关性计算.[5]在LMS Virtual.Lab 12软件中同时导入试验结果文件和有限元结果文件进行分析，在容差为4 mm时，试验模型节点与有限元模型节点全部匹配.程序配电器箱体相关性分析结果见表1.由此可以看出：通过试验修正，前6阶振型的置信度较高，有限元模型和试验模型振型基本一致，可以进行后续分析计算.

关注50 Hz以内频率范围，根据箱体特性的分析，其1阶固有频率为270 Hz左右，远远高于分析频率范围，因此在后续分析中可将箱体的结构视为刚体.

3.3减振器的模拟

减振器的安装剖视图见图7.

该减振器的材质为橡胶，阻尼橡胶通过金属垫圈、滑板和配合孔支撑.垫圈和通孔使用螺钉将仪器与支架连接在一起.这类橡胶减振器在轴向与径向上都有减振作用，可达到三维减振效果.[6]

减振器仿真结果见图8.主要考虑橡胶减振器的三维减振作用和减振器安装方式，两边的橡胶阻尼圈的主要作用为轴向减振，中间2个橡胶阻尼圈主要作用为径向平面减振.在箱体与螺钉之间分别建立RBE3单元模拟减振器的安装方式并在两者之间赋予其弹簧（SPRING）特性，具体刚度通过测量和修正有限元模型确定，见表2.支架与箱体之间建立弹簧单元，以此三向正交的弹簧单元模拟橡胶减振器的三维方向减振作用.

3.4支架有限元建模

程序配电器整体有限元模型见图9.

图 9程序配电器有限元模型

Fig.9Finite element model of program distributor

仪器支架主要由薄板和肋板组成.在建立几何模型时忽略一些无关大局的过渡圆角，使得大多数网格可以划分为精度较高的六面体单元，只有少部分不规则的单元，不影响整体模型精度.最终模型节点数为49 494个，六面体单元数为25 124个.模型的坐标系取轴向为y轴方向，径向为x和z轴方向.

4减振器螺栓连接的动强度分析

4.1结构模态分析

使用MSC Nastran求解器，采用Lanczos法对有限元模型进行模态求解，结果见表3.

从模态分析结果和实际试验情况2方面考虑，重点关注第2，3和4阶的频率和振动情况.对结构进行谐响应分析，结果显示第4阶固有频率处对应的位移峰值远大于其他固有频率处的峰值，对结构的破坏程度最大，故本文仅对第4阶固有频率进行分析，其他各阶频率分析方法是一样的.

4.2减振器刚度对固有频率的影响

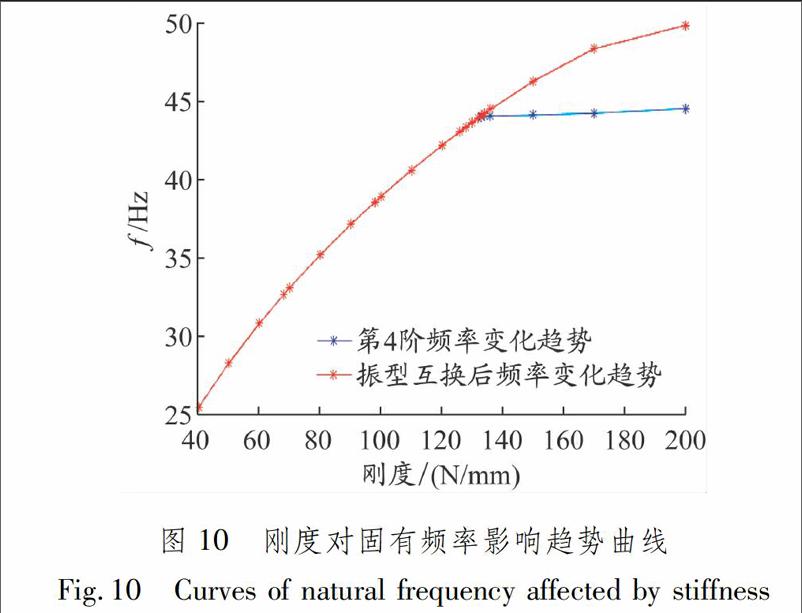
沿x向弹簧的刚度记为k1，沿y向弹簧的刚度记为k2，沿z向弹簧的刚度记为k3，由减振器的对称性可取k3=k2.由仿真结果分析可知，第4阶固有频率由k2和k3决定.对不同刚度的减振器模型进行模态分析，仿真计算22组不同刚度值下的固有频率.当刚度增大到133 N/mm时，第4阶（刚度为40～133 N/mm）与第5阶（刚度为133～200 N/mm）振型互换.刚度对固有频率影响趋势曲线见图10.由图10可知：固有頻率随着减振器刚度的增加而增大，当刚度值较小时频率增长速度较快，随后固有频率趋向于稳定值45 Hz.[7]

4.3动力学分析

在程序配电器的结构性能分析中，结构强度是最为关注的问题之一.结构强度是保证仪器支架结构可靠性的重要指标.从结构设计方面来说，减振器螺钉是关键部件.结构在振动过程中可能产生较大的放大作用，在不同的工况下螺钉将承受很大的交变载荷，对强度要求很高.[810]因此，有必要分析螺钉的动强度，为螺钉的选材和结构改进提供依据.

4.3.1结构的动力学响应分析

由谐响应的分析结果可知，最大峰值在32.57 Hz处.施加正弦激励，频率设置为谐响应最大峰值处频率32.57 Hz，量级为8.4g，激励施加位置与实际情况一致，可得到螺钉的加速度曲线，见图11.y向加速度最大峰值达到32g，是激励的3～4倍，呈现显著的放大效应.

4.3.2螺钉的弹塑性分析

由于采用正弦激励分析螺钉受力是基于直接瞬态响应理论的，所以有必要对螺钉进行材料的弹塑性分析.将螺钉简化为悬臂状态[11]，由正弦激励仿真箱体加速度的大小估算得到每个螺钉的受力大小为800 N（y向），计算得到其von Mises应力分布云图和等效塑性应变云图，见图12和13.

有限元仿真采用理想弹塑性模型，屈服应力设为805 MPa，刚性屈服时塑性应变为0，等效塑性应变大于0时说明材料发生屈服.仿真结果显示最大应力为1 023 MPa，超过材料的屈服极限，等效塑性应变大于0，所以螺钉在800 N集中力的作用下发生屈服.同时，改变集中力的大小，分别为600，650和700 N，对螺钉进行分析，集中力为650和700 N时螺钉也发生屈服.实际上，螺钉在交变载荷的作用下会受到较大的剪切力作用.

仿真分析结果显示对应测点的加速度发生3～4倍的放大，螺钉出现屈服现象，与试验结果一致，说明本文对程序配电器的分析研究有效，模拟振动试验中低频段正弦扫频试验摸底试验循环（30～50 Hz，8.4g）出现螺钉弯曲现象，为程序配电器的结构设计、螺钉材料和减振器设计提供依据.

5结束语

本文提出一种适用于程序配电器的减振器的连接方式以及仪器设备的有限元建模方法，通过对箱体模态分析结果与试验结果的比较，证明方法的可行性.仿真结果表明减振器的等效刚度是影响程序配电器固有频率的重要因素，因此减振器的合理调整是优化程序配电器结构动力学特性的关键技术.将支架与箱体通过减振器的连接构成结构体，提出一种考核关键部件动强度的方法，通过对结构进行直接瞬态响应分析、对关键部件进行等效静力分析，与试验结果进行比较，证明方法可行.

参考文献：

[1]孙伟， 李以农， 刘万里， 等. 橡胶隔振器非线性动态特性建模及实验研究[J]. 振动与冲击， 2012， 31（23）： 7176. DOI： 10.13465/j.cnki.jvs.2012.23.017.

SUN W， LI Y N， LIU W L， et al. Dynamic modeling and test for a nonlinear rubber damper[J]. Journal of Vibration and Shock， 2012， 31（23）： 7176. DOI： 10.13465/j.cnki.jvs.2012.23.017

[2]FAN R， MENG G， YANG J， et al. Experimental study of the effect of viscoelastic damping materials on noise and vibration reduction within railway vehicles[J]. Journal of Sound and Vibration， 2009， 319（12）： 5876. DOI： 10.1016/j.jsv.2008.03.071.

[3]机械设计手册编委会. 机械设计手册： 机械振动和噪声[M]. 北京： 机械工业出版社， 2007： 6973.

[4]韩德宝， 宋希庚， 薛冬新. 橡胶减振器非线性动态特性的试验研究[J]. 振动工程学报， 2008， 21（1）： 102106. DOI： 10.16385/j.cnki.issn.10044523.2008.01.006.

HAN D B， SONG X G， XUE D X. Experiment on nonlinear dynamic characteristics of rubber isolator[J]. Journal of Vibration Engineering， 2008， 21（1）： 102106. DOI： 10.16385/j.cnki.issn.10044523.2008.01.006.

[5]李伟， 涂奎， 李先文. 摩托车车架模态分析与验证[J]. 重庆理工大学学报（自然科学版）， 2011， 25（3）： 1114. DOI： 10.3969/j.issn.16748425B.2011.03.003.

LI W， TU K， LI X W. Analysis and verification of motorcycle frame modal[J]. Journal of Chongqing University of Technology（Natural Science）， 2011， 25（3）： 1114. DOI： 10.3969/j.issn.16748425B.2011.03.003.

[6]刘立新. 基于MSC Patran/Nastran 的组合仪器支架模态分析方法[J]. 航天制造技术， 2012（1）： 3337.

LIU L X. Modal analysis method for combination instrument framework based on MSC Patran/Nastran[J]. Aerospace Manufacturing Technology， 2012（1）： 3337.

[7]和法家， 盧曦. 某直升机橡胶减震器动刚度特性试验[J]. 实验室研究与探索， 2014， 33（3）： 41 44.

HE F J， LU X. Experimental research on dynamic stiffness characteristics of a rubbershockabsorber[J]. Research and Exploration in Laboratory， 2014， 33（3）： 41 44.

[8]施荣明. 现代战斗机结构动强度设计技术指南[M]. 北京： 航空工业出版社， 2012： 193197.

[9]徐晓晨， 刘波， 贾宏光， 等. 冲击载荷下复合材料板簧式起落架动强度研究[J]. 机械强度， 2013， 35（5）： 571576. DOI： 10.16579/j.issn.1001.9669.2013.05.019

XU X C， LIU B， JIA H G， et al. Dynamic strength of landing gear made of composite materials under impact load[J]. Journal of Mechanical Strength， 2013， 35（5）： 571576. DOI： 10.16579/j.issn.1001.9669.2013.05.019

[10]JINDAL V K， MOHSENIN N N. Analysis of a simple pendulum impacting device for determining dynamic strength of selected food materials[J]. Transactions of Asae， 1976， 19（4）： 07660770. DOI： 10.13031/2013.36113.

[11]汤传军， 张键， 李健， 等. 基于Workbench变速器齿轮轴的疲劳分析[J]. 汽车实用技术， 2014（2）： 1 4.

TANG C J， ZHANG J， LI J， et al. Fatigue analysis of transmission gear shaft based on Workbench[J]. Automobile Applied Technology， 2014（2）： 1 4. DOI： 10.3969/j.issn.16717988.2014.02.002.（编辑武晓英）