基于数学核心素养的解析几何教学*——谈数学运算能力的提升

●张 岚(慈溪中学 浙江慈溪 315300)

基于数学核心素养的解析几何教学*
——谈数学运算能力的提升

●张 岚
(慈溪中学 浙江慈溪 315300)

数学运算是数学六大核心素养之一，数学运算素养的具体内容体现了对学生数学运算能力培养有序推进的步骤.而解析几何借助坐标系，用代数方法研究几何问题，问题一般涉及的变量多，运算量大，是考查数学运算能力的重要载体.文章以解析几何教学为载体，从分析题意、设计算法、题后反思等维度谈谈课堂教学中数学运算能力的提升，以及反思课堂教学中应注意的几个重要环节.

数学核心素养;运算能力;解析几何教学;教学反思

随着教育部《关于全面深化课程改革落实立德树人根本任务的意见》的发布，“核心素养”成为热门词汇[1].数学核心素养不是指具体的知识与技能，而是强调获取数学知识、解决实际问题的思维品格和综合能力.数学核心素养不是与生俱来的，是在数学学习过程中逐步形成的，是可以通过数学学习、反思、积累、应用的过程逐渐养成的.

“如何在课堂教学中落实数学核心素养？在教学过程中，如何寻找培养学生核心素养的有效途径？”这是值得每位教师思考的问题.笔者以解析几何教学为载体，重点谈谈关于提升学生数学运算能力的一些想法.

1 试题再现

图1

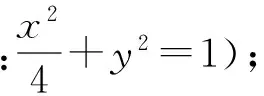
2 运算教学的课堂实践

2.1 分析题意，明确运算方向

师：解决第2)小题的关键是什么？

生1：关键是条件|CM|=|DN|的转化.

师：该如何转化呢？

生1：线段长度用两点间距离来表示:

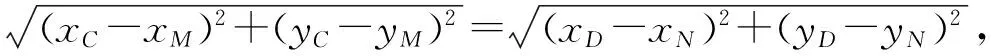
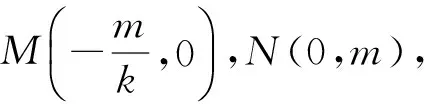
师：的确，变量多会阻碍式子的化简.那如何减少变量呢？

生2：因为这些点都在直线上，所以可以利用y=kx+m，将所有的纵坐标y用横坐标x来表示，可得

即

生3：老师，这不就是弦长公式吗？

师：生2的回答展示了弦长公式的推导过程.当2个点在同一条直线上时，可以用弦长公式来表示两点间距离，这比直接用两点间距离公式要简洁很多.接下来该如何整理这个式子呢？

生4：因为直线和椭圆相交，所以我想应该和韦达定理联系起来，尝试去掉绝对值，可得

从而

xM+xN=xC+xD，

正好可以应用韦达定理来表示.

师：非常好.通过大家的讨论，通过条件的转化，得到一个简洁对称的数学表达式，这个式子有什么意义呢？

生5：说明线段MN和线段CD的中点重合.

生6：用坐标表示斜率，可得

再结合点C,D在直线y=kx+m(其中k>0)上，消去y化简式子.

设计意图 仔细审题、分析题目、弄懂题意是解题运算的基础，有助于学生理解运算对象，从而探索正确的运算方向.在课堂上，教师应重视引导学生将题目条件逐一进行转化，用恰当的数学式子进行表示，培养学生数学抽象和转化化归的能力.此题分析的探索过程，渗透了转化化归、数形结合等丰富的数学思想方法，也有效地提升了学生的逻辑思维能力.

2.2 设计算法，求得运算结果

在运算方向的指引下，学生在课堂上动手操作，设计运算求解的程序，力求得到正确的运算结果.

(4k2+1)x2+8mkx+4m2-4=0,

从而

Δ=64m2k2-4(4k2+1)(4m2-4)>0,

即

4k2-m2+1>0,

于是

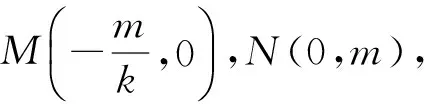
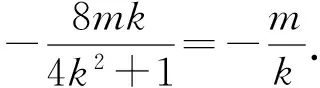
将韦达定理代入得

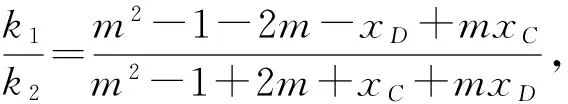
那么此式该如何计算？

(大家不禁佩服生8的运算能力，变繁为简，化腐朽为神奇!)

又直线y=kx+m(其中k>0)与线段F1F2、椭圆短轴分别交于点M,N(点M,N不重合)，从而

师：生9将题意分析得很透彻，考虑非常全面，大家做题时也要仔细寻找线索.现在万事俱备，只欠结果了，请大家算一算吧.

(教师巡视，指出学生运算中的错误.)

设计意图 在明确运算方向后，关键就在于掌握正确的运算法则，求得正确的运算结果.运算能力的培养，需要教师舍得花时间在课堂上板演，或者舍得花时间让学生进行运算求解、展示解题过程，然后师生共同分析错误原因，最后求得正确结果.若课堂上只讲解题思路分析，不讲计算过程，则学生碰到类似的计算很可能就无从下手，直接放弃.只有在课堂上重视运算求解的过程，才能使学生重视运算求解，并在运算的过程中掌握运算法则，领会运算技巧，避免运算错误，提高运算的正确性，真正提升数学运算的能力.

2.3 题后反思，提升运算能力

下面只要应用韦达定理就可以表示这个式子了，化简得

此时，又有生12提出：利用我们所习得的结论:在椭圆中，

得

然后利用韦达定理，代入运算即可.

师：生12能将所学知识灵活应用，融会贯通，值得我们学习.通过今天的解析几何运算学习，你有什么体会？大家可以相互交流，并应用到以后的学习中去.

设计意图 题后总结反思是提升解题能力、提高学生素养的必经之路.反思解题方法，反思运算过程，反思知识的前后联系，能使学生更全面地认识问题的本质.解题方法的多样性有助于拓展学生的思维，有助于分析各种解题方法的优劣获得问题的最优解，有助于解题经验的积累和交流，有助于提高运算能力、提升问题解决的能力.

3 数学运算教学的思考

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程.主要包括：理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等.数学运算素养的表现形式，体现了对运算要求的层层递进，也体现了教学中有序推进运算能力培养的步骤.而解析几何借助坐标系，用代数方法研究几何问题，问题一般涉及的变量多，运算量大，是考查数学运算能力的重要载体[2].解析几何教学中渗透数学运算能力的培养，可以从以下几个方面入手:

3.1 理解概念，夯实运算根基

高中阶段整个数学体系是由概念组建起来的，概念教学的重要性不言而喻，准确理解概念是运算成功的重要根基.而学生产生错误的原因之一就是概念理解出错，或者概念理解不全.例如第1)小题求椭圆的标准方程，就是对概念的考查，有些学生会误把长轴长当成a的值来计算，出现错误.

因此,教师在课堂上要把概念讲清讲透，挖掘概念的内涵外延，建立概念之间的联系，强化学生对概念的理解和掌握，并以题组的形式加以辨析.从形到数，从数到形，相互结合，这样才能完善概念的认知结构，真正意义上做到理解运算对象，在解题中多一份胜算.比如“问题串”的设计就是一种行之有效的教学策略，引领着学生的思维朝着正确的方向发展，进而促成数学素养的养成.

3.2 掌握模型，获得运算经验

培养学生解决解析几何问题的能力，首先要加强基础题型训练，使学生清晰地理解、记忆基本公式与定理，掌握基本技能和方法，通俗地讲就是弄清楚套路，力求达到规范、熟练、快捷的程度，直至获取基本的数学运算经验.

3.3 转化化归，明确运算方向

培养学生的转化化归能力，需要重视解题思路的分析，需要充分挖掘所求问题的代数特征和图形特征，寻求与已有知识的契合点，并以此为切入点进行解题.将问题转化为与原问题等价且易于解决的问题，与已有的解题经验相结合，将陌生变为熟悉，使原本看起来比较棘手的问题柳暗花明.

3.4 优化策略，提升运算

3.5 强化计算，突破运算难关

学生在明确运算方向、设计运算程序之后，与求得正确的运算结果还有一段距离.虽说只有一步之遥，却也会发生“错一步，满盘皆输”的局面.那么作为教师，应该引导学生重视运算的思维过程，鼓励学生敢算、多算.一方面教师在课堂中应重视运算过程的演示、算法分析，不可以一句“课后自己去算”草草了事.另一方面，教师在课堂中要舍得留出时间，放手让学生运算，要给学生产生错误、展现错误的机会，从而一起分析产生错误的原因，修正错误的运算环节.通过一次次的出错、纠错、反思、总结，慢慢悟出正确的运算方法和运算结论，提升运算能力，形成一丝不苟、严谨求实的科学精神.

总之，数学运算能力的提升是一个循序渐进、螺旋上升的过程.教师要做好教学的顶层设计，站在系统的高度规划好达成教学目标的每一步骤，引领学生逐步提升数学素养.

[1] 章建跃.高中数学教材落实核心素养的几点思考[J].课程教材教法，2016(7):44-49.

[2] 赵国胜.将运算进行到底——以解析几何教学为契机,培养学生的运算能力[J].数学教学通讯,2013(36):26-29.

2017-02-27；

2017-03-29

张 岚(1981-)，女，浙江慈溪人，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)05-27-04