数学原理教学方法*——以“由平行线截得的比例线段”为例

●邬云德(石浦中学 浙江象山 315731)

数学原理教学方法*
——以“由平行线截得的比例线段”为例

●邬云德
(石浦中学 浙江象山 315731)

在以“由平行线截得的比例线段”为载体的研修活动中发现，课堂教学普遍没有遵循原理教学的基本规范．鉴于此，文章在重复式观课与反思基础上，对该课的教学进行重建，改进后的教学过程与效果得到了同仁认可．

数学原理；比例线段；教学方法；案例分析

1 背景介绍

数学原理是在观察、实践的基础上，经过归纳、概括得出的普遍规律或基本方法，它包括数学中的事实、运算律、法则、方法、规律等．一般地，数学原理教学要经历“提出问题→操作观察→归纳猜想→多样表达→解决问题→反思内化”的基本过程．但在以浙教版《数学》九年级上册第4.2 节“由平行线截得的比例线段”为载体的“多人同课异构”式的研修活动中发现，课堂教学普遍没有遵循原理教学的基本规范．笔者查阅网上同类课例发现也有类似现象．鉴于此，笔者在重复式观课与反思基础上，对该课的教学进行重建，改进后的教学过程与教学效果得到了同仁的认可．现将其整理出来，以飨读者．

2 教学实录

环节1 经历回顾并提出问题的过程——明确研究问题

师：如图2，若将“DE是△ABC的中位线”改为“3条等距离的平行线”，则上述结论成立吗？为什么？

生1：上述结论同样成立．因为3条平行线等距离，所以AD=DB，AE=EC．

师：不错．一般地，若3条等距离的平行线截2条直线，则所得的对应线段成比例吗？

生2：同理可得，所得的对应线段成比例．

师：由此，还能推演出哪些真命题？

生3：若4条等距离的平行线截2条直线，则所得的对应线段成比例．

生4：若n条等距离的平行线截2条直线，则所得的对应线段成比例．师：一般地，如图3，若l1,l2,l3,l4，…是一组等距离的平行线，l与m是任意画的2条直线(相交或平行)，分别与这组平行线依次相交于点A，B，C，D，…和A′，B′，C′，D′，…，则

因为平行线等距离，所以

AB=BC=CD=…，

A′B′=B′C′=C′D′=…,

反之也成立．

师：如图4，若将图1中的△ADE绕点A逆时针方向旋转180°，则

图4 图5

师：若将图4改成图5(3条直线互相平行)，则由图4推出的结论同样成立吗？为什么？

生5：这些结论同样成立．因为这2个图形没有实质性变化．

环节2 探索由平行线截得的比例线段——形成基本事实

师：现在请大家先依次完成下列任务．

1)按题意画出形如图3所示的图形;

2)测量有关线段的长度，如AB，BC和A′B′，B′C′;

(教师等待学生完成任务.)

师：大家通过测量、计算，所画的图形对应线段成比例吗？

生(众)：所画的图形对应线段成比例．

师：只要所画的图形符合要求，并且测量准确，就能验证对应线段成比例．大家课后也可用几何画板来验证．这样我们可以得到以下基本事实：2条直线被一组平行线(不少于3条)所截，所得的对应线段成比例．

师：这个基本事实是推导后续内容的依据，并在几何计算与作图中经常会用到．其实，这个基本事实也可以证明，有兴趣的同学可以在课后探索其证明方法．

环节3 参与尝试该事实应用的活动——合作解决有代表性的问题

师：现在我们一起来解决问题1．

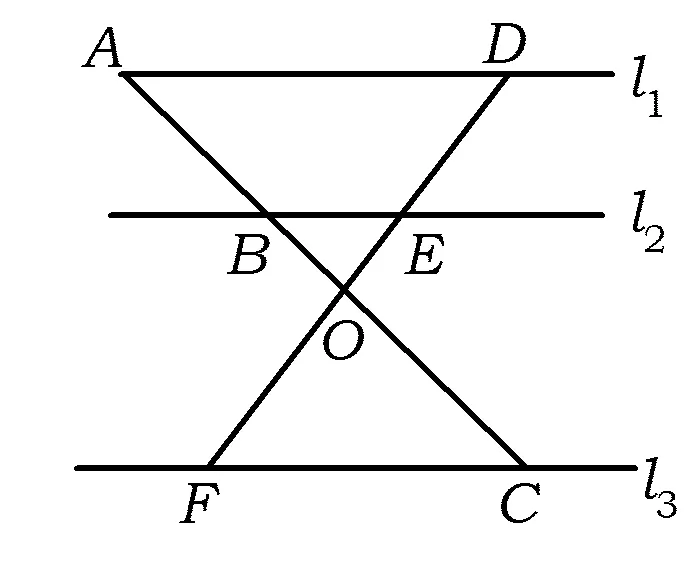
图6

问题1 如图6，直线l1∥l2∥l3，直线AC分别交l1,l2,l3于点A，B，C,直线DF分别交l1,l2,l3于点D，E，F．已知DE=3，EF=6，AB=4，问：AC的长是多少？

师：因为l1∥l2∥l3，所以有许多对应线段成比例的关系式．这里需要怎样的关系式？

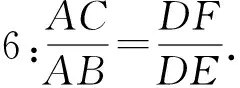
师：我们要找出有关线段(已知线段和所求线段)成比例的关系式．

师：在这个比例式的4个量中，已知3个量，能求第4个量吗？

师：请大家把计算过程规范地写出来，若有困难，可参考课本中的书写过程．

(教师等待学生完成任务.)

师：如图6，若AB=DE，EF=5，则BC的长是多少？为什么？

师：不错．如图6，若OB=ED，OE=3，AB=4，则OA的长是多少？

师：生9运用了方程思想，解决这类问题经历了哪几个步骤？

生10：先根据基本事实列出成比例的关系式，再用解方程的方法求出有关线段的长．

师：方程思想在几何计算中会经常用到．现在我们一起来解决下列问题2．

问题2 已知线段AB，怎样将线段AB五等分？

师(稍停顿后)：如果解决这个问题有困难，我们可以先退一步：怎样将线段AB二等分？

生11：作线段AB的垂直平分线，垂足点就是线段AB的二等分点．

师：不错．还有其他方法吗？

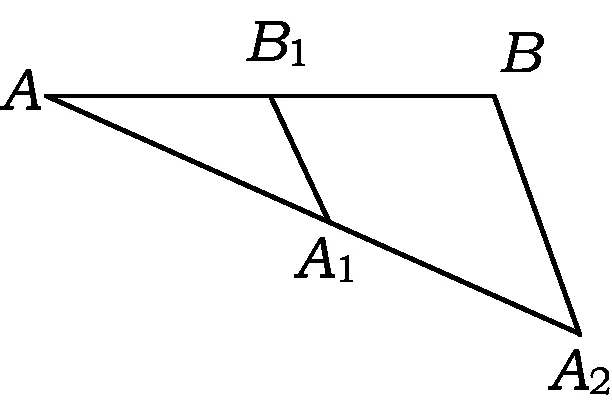
图7

(全体学生有点困惑,很期待新方法.)

师：如图7，若AA1=A1A2，A1B1∥A2B，则AB1=B1B吗？为什么？

师：这就是说，可用基本事实将线段AB二等分．那么怎样将线段AB三等分？

生13：先以A为端点作一条射线，并在射线上依次截取线段AA1=A1A2=A2A3，再联结A3B，并过点A1，A2分别作A3B的平行线，依次交AB于点B1，B2，则B1，B2就是所要求作的把线段AB三等分的点．

师：现在能将线段AB五等分吗？

生(众)：能．

师：请大家在白纸上画一条线段AB，并将其五等分．

(教师等待学生完成任务.)

师：能将已知线段n等分吗？

生14：用同样的方法能将已知线段n等分．

师：能将线段AB分成AC,CB这2条线段，并使AC∶CB=2∶3吗？

生15：问题可转化为将线段AB五等分．

师：不错．生15运用了化归思想．这些作图方法的理论依据是什么？

生16：其理论依据是基本事实．

师：下面请大家完成课本中的练习题．

(待学生完成任务后，教师组织学生交互反馈与评价．)

环节4 参与回顾与思考的活动——合作进行反思与总结

师：本节课研究了哪些内容？在学习过程中，你有哪些体会和收获？

生17：本节课研究了基本事实和它在计算与作图中的应用．

生18：从已知结论出发，特殊到一般探索是发现新命题的方法．

生19：画图、测量、计算，也是发现数学结论的方法．

生20：学习数学要善于提出问题，反思是学习数学的重要方法．

生21：用基本事实进行计算的关键是列成比例的关系式．

生22：解决复杂的问题可采用以退求进的策略．

……

师：这些收获与体会非常有价值，对后继学习有指导作用．

3 教学分析

数学原理是一些浅显易懂的现象或道理，如运算中的交换律、结合律、分配律等都是基本的道理．但“基本”不是肤浅，而是根本、重要．原理教学可以借用“概念形成”的方式来进行，其思维形式是归纳．它只要接受实践的检验即可，不必经过逻辑的证明，它可以成为推导后续内容的依据．由于原理是事物之间的普遍规律，通常表现为一些数学对象之间的关系或表达式，因而原理学习要启发学生从内容、意义、适用范围等方面去理解，要应用原理去解决问题[1]．

本节课中的基本事实是基础知识，是解决有关计算与作图问题的重要工具．它形成与应用的过程和所蕴含的归纳思想、数形结合思想、方程思想、化归思想等及特殊到一般的探索策略和画图、测量、计算的探索方法，对发展学生的智力、能力和个性有积极的影响．该基本事实的教学性质是原理教学，全面发挥其育人功能，需要教师根据原理教学的基本规范，设计并组织有效的数学活动．但目前在该课的教学中，大多数教师没有引导学生经历原理教学完整的认知过程，也没有留给学生充足的“自主思考与实践时间”和“合作交流机会”．这不能满足学生感悟思想、积淀经验及发展能力与个性的需要．

本课例在“精致化”分析的基础上，将其教学立意于过程教育，并以课本提供的题材为载体，从学生已有的知识与经验出发，运用教师价值引导与学生自主建构相结合的适度开放的方式，引导学生经历完整的认知过程．在“回顾并提出问题”的教学中，既有根据三角形中位线定理的几何模型给出有关结论的过程，以激活学习新知识所需要的“生长点”，又有“变式、联想”基础上提出问题的过程，以发展学生特殊到一般的合情推理能力和明确本课所要研究的问题．在“探索由平行线截得的比例线段”的教学中，既有“画图→测量→验证→概括→表达”的过程，以发展学生的探索能力、积累探索的经验和获得基本事实，又有获得基本事实之后的教师讲述，以揭示基本事实的应用价值及可以进行思考的问题．

在“解决问题1”的教学中，既有分析并解决问题1的过程，以巩固基本事实和发展智慧技能，又有解决问题之后的变式，以达到灵活运用基本事实的程度．在“解决问题2”的教学中，既有特殊到一般的探索过程，以感悟以退求进的策略和明确解决问题的方法，又有解决问题之后的变式与拓展，以感悟化归思想和加深对作图方法的认识．

参与研修的教师普遍认为：本课例遵循了原理教学的基本规范，体现了过程教育和以学为中心思想，统筹兼顾了过程与结果，能实现“能发现并会陈述基本事实，会结合图形写出对应线段成比例的关系式，能在探索过程中有个性化表现，能感悟所蕴含的归纳思想和积淀发现与提出问题的经验；会用基本事实进行有关计算和作图，能在计算过程中感悟数形结合思想和方程思想等，能在作图过程中感悟化归思想和特殊化试探的策略，能积累几何计算与作图的数学活动经验”的教学目标；特别是“回顾与提出问题”的教学，有助于学生发展合情推理能力和积淀发现与提出问题的经验．

因此，一般地，数学原理教学要经历“提出问题(从具体问题或特殊问题出发)→操作观察(通过画图、实验、计算等，观察事物间的关系)→归纳猜想(由特殊猜想一般)→多样表达(口头、数学文字、数学符号表达)→解决问题(解决数学内部与外部问题)→反思内化(感悟研究过程和所蕴含的数学思想及积淀数学活动经验)”的过程，并在组织实施教学活动时，要留给学生足够的自主思考与实践的时间和合作交流的机会，要发挥教师在教学活动中的主导作用，要合理评价学生在教学活动过程中的表现，以促使学生对原理的认识达到一定的“深度”和“宽度”，促使学生学会主动提出问题，独立思考问题，合作探究问题及养成敢于质疑、善于表达、认真倾听、勇于评价和不断反思的良好品质和习惯．

本课例在农村中学实施后，发现时间有点紧张，可见体现过程教育的课堂教学，有时会对按时完成教学任务带来挑战．解决这个问题的策略：一是运用课内外结合的方法——课前预习教师设计的“导学案”[2]；二是根据学生的现实来确定过程与结果的平衡点——尽管过程与结果两者不能偏废，但结果是主要的、基本的，而相对来说过程是次要的、从属的．

[1] 罗增儒．课堂教学的创新永远在路上[J]．中学数学教学参考，2016(7)：29．

[2] 邬云德．例谈“先行组织者”教学方式及其成效[J]．中学教研(数学)，2012(11)：9-12．

2016-12-19；

2017-02-10

邬云德(1956-)，男，浙江奉化人，浙江省特级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)05-21-04