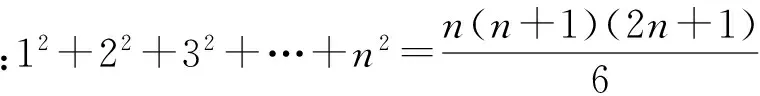寻找结构差异 深究解题策略*
——一道高考三角题的解法探究与思考
2017-05-12宫前长天水市第一中学甘肃天水741000
●宫前长(天水市第一中学 甘肃天水 741000)
寻找结构差异 深究解题策略*
——一道高考三角题的解法探究与思考
●宫前长
(天水市第一中学 甘肃天水 741000)
数学的学习离不开解题.研究高考试题,不仅要学会审题、解题,而且要弄清题目条件与结论之间各种思维通道的差异,并且通过结构差异,深究解题策略的优化方案,能够从中提炼出数学思想方法,提升学生数学的思维能力.
思维认知;试题探究;结构;思维价值
1 试题呈现
例1 在锐角△ABC中,若sinA=2sinB·sinC,则tanA·tanB·tanC的最小值是______.
(2016年江苏省数学高考试题第14题)
2 查清结构
从题目来看,以解三角形为背景命制试题,主要考查分析、解决三角形问题的能力,以及两角和与差的三角函数公式、正弦定理和余弦定理等知识点的综合运用能力.同时,强化对转化与化归、函数与方程、消元与不等式求最值等数学思想方法的考查.命题人从知识的整体高度与数学思维的价值取向上命题,试题结构简单,形式简洁、明了,但其内涵丰富,是一道值得多视角探究和深思的好题.
2.1 审清条件
试题限于锐角三角形,强调了3个内角的范围,以及深挖隐藏的条件“3个内角的和:A+B+C=π”,结合题设给出的条件“sinA=2sinB·sinC”,其结构表征要求必须借助两角和与差的三角函数公式、正弦定理和余弦定理等知识点来探究解题思路、方法.
由于条件sinA=2sinB·sinC中有3个角,就会自然想到消元,联想到在三角形中,常用三角等式sin(B+C)=sinA,cos(B+C)=-cosA来减少变量.
根据两角和的三角函数诱导公式展开,其具体变形为
sinA=sin(B+C)=sinB·cosC+cosB·sinC,
再结合条件sinA=2sinB·sinC可得
sinB·cosC+cosB·sinC=2sinB·sinC.
此时,按照变形所得的三角等式结构sinB·cosC+cosB·sinC=2sinB·sinC,突发奇想,将形成好多解题的思路与方法.
2.2 审查结论
审题是解题中最重要的一个环节,审题的视角、方法直接关系到解题的成功与否.数学问题中的结论,往往会给审题提供一些重要的信息.如“tanA·tanB·tanC的最小值”明确指出了代数式tanA·tanB·tanC的化简(求解)方向:多变量的最小值问题.但从代数式的结构tanA·tanB·tanC上看是三角形的3个内角的正切值的积,依照平时做题习惯,会采用“切化弦”技术减少变量的个数,将问题转化为含有2个变量或1个变量的问题,通过求最值问题,熟悉化简求解的原则和方法.
在锐角三角形中,依两角和的正切公式有
变形可得
tanA·tanB·tanC=tanA+tanB+tanC.
这样处理,使得结构复杂的tanA·tanB·tanC等价转化为tanA+tanB+tanC,与条件关系式相比,结构差异缩小了,不再产生解题心理压力,好的解题思路方法不断涌出.
2.3 审明联系
通过题设条件、结论的剖析,如何更好地架设条件与结论之间的“桥”?让“sinA=2sinB·sinC”到“tanA·tanB·tanC”的“天堑”变“通途”.已知条件等式sinA=2sinB·sinC只含有正弦,而所求问题式中只含有正切tanA·tanB·tanC.因此,审题时很自然地想到一种策略:“弦化切”或“切化弦”.此时,关键等式来源于“sinB·cosC+cosB·sinC=2sinB·sinC”的2边同时除于“cosB·cosC”(在锐角△ABC中,cosB·cosC≠0)得到等式“tanB+tanC=2tanB·tanC”,很好地消除了条件与结论之间的差异.
结合平时的解题经验,想到另一种策略:“等价转化法”,即将三角问题转化为代数问题进行求解.
总之,通过上述的审题,初步形成如下的解题思维链(如图1所示):
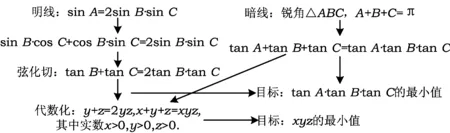
图1
3 解法探究
3.1 弦化切
将条件等式“弦化切”,再与两角和的正弦、正切公式以及锐角三角形的恒等式等知识点结合,然后进行有效化简,“接通”条件与目标,求得tanA·tanB·tanC的最小值.
解法1 (均值不等式法)
sinA= sin(B+C)=sinB·cosC+cosB·sinC=
2sinB·sinC,
因为△ABC为锐角三角形,所以cosB>0,cosC>0,所以
tanB+tanC=2tanB·tanC.
又A=π-(B+C),从而
于是tanA·tanB·tanC=tanA+tanB+tanC=
整理得
tanA·tanB·tanC≥8,
当且仅当tanA=4时等号成立.故tanA·tanB·tanC的最小值是8.
解法2 (基本不等式法)由解法1中tanB+tanC=2tanB·tanC,可知

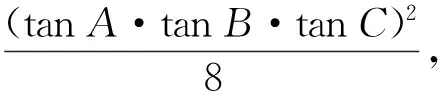
tanA·tanB·tanC≥8,
当且仅当tanA=tanB+tanC,即tanA=4时等号成立.故tanA·tanB·tanC的最小值是8.
解法3 (基本不等式法)由解法1,知
tanB+tanC=2tanB·tanC,
则
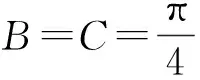

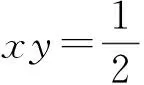
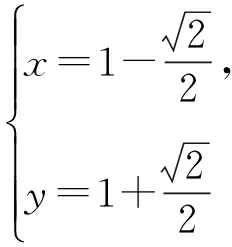
故tanA·tanB·tanC的最小值为8.
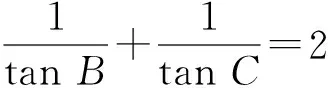
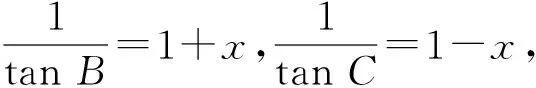
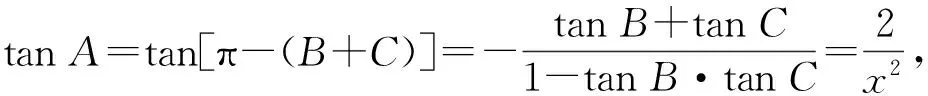
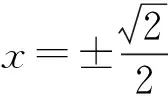
解法4 (整体法)由解法1知
又
tanB+tanC=2tanB·tanC,

把tanB·tanC看成一个整体,令tanB·tanC=t(其中t>1),则问题转化为求
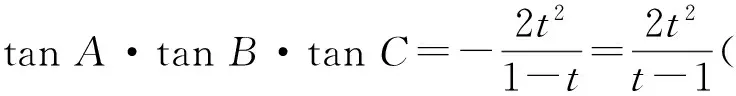
的最小值.
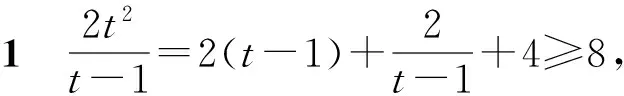
当且仅当t=2∈(1,+∞),即tanA=4时,tanA·tanB·tanC的最小值为8.
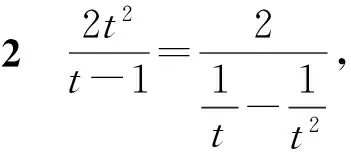
则
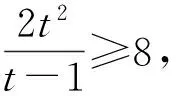
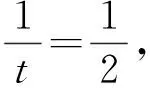
解法5 (判别式法)由解法1知
由三角形恒等式知
联立式(1)和式(2),解得
tanA+2tanB·tanC=tanA·tanB·tanC,
从而
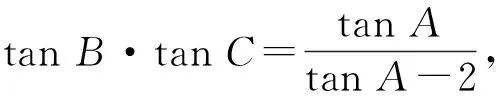
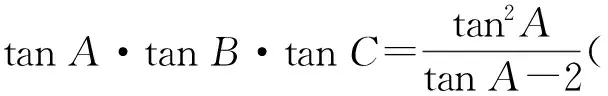
因为△ABC为锐角三角形,所以
tanA·tanB·tanC>0,
不妨设tanA·tanB·tanC=y(其中y>0),则
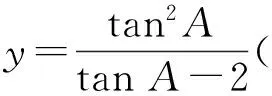
变形为关于tanA的一元二次方程
tan2A-ytanA+2y=0.
由判别式Δ=y2-8y≥0,得y≥8.故tanA·tanB·tanC的最小值为8.
解法6 (构造函数法)由解法5知
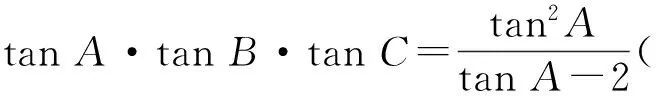
目标tanA·tanB·tanC的最小值问题转化为关于tanA的函数最小值问题.
当且仅当tanA=4时等号成立.故tanA·tanB·tanC的最小值为8.
解法7 (对偶构造法)已知sinA=2sinB·sinC,得
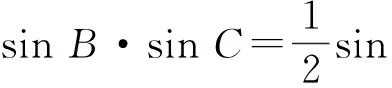
(3)
由锐角△ABC,得
cosA>0, cosB>0, cosC>0.
设 cosB·cosC=tcosA,
(4)
式(3)÷式(4),得
式(4)-式(3),得
化简得
即
tanA=2(1+t),

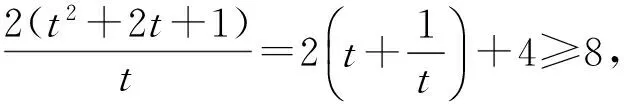
当且仅当t=1时,tanA·tanB·tanC的最小值为8.
3.2 切化弦
将结论tanA·tanB·tanC切化弦,再与两角和的正弦、正切公式,锐角三角形的恒等式,以及函数最值等知识点结合,求得tanA·tanB·tanC的最小值.
解法8 (消元法)
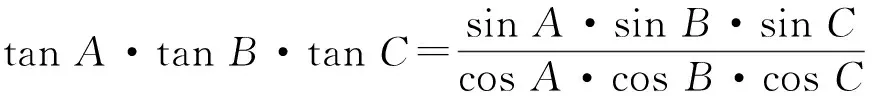
因为sinA=2sinB·sinC,由锐角△ABC,得
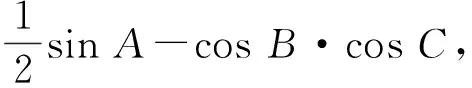
方法1 (判别式法)令
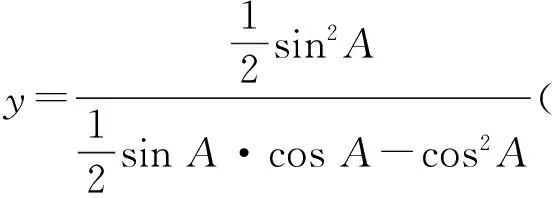
化简得 sin2A-ysinA·cosA+2ycos2A=0.
由锐角△ABC,得cosA>0,上式2边同除cos2A得
tan2A-y·tanA+2y=0,
此方程可看成是关于tanA的一元二次方程,则由判别式Δ=y2-8y≥0(其中y>0),得y≥8.故tanA·tanB·tanC的最小值为8.
方法2 (判别式法)令
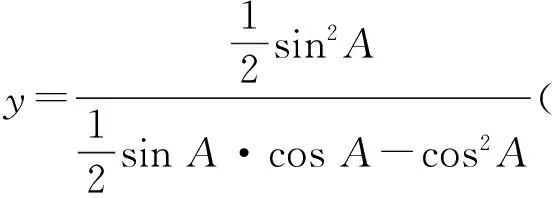
化简得 sin2A-ysinA·cosA+2ycos2A=0,
将此等式看成是关于sinA的一元二次方程,求得判别式
Δ=y2cos2A-8ycos2A=
(y2-8y)cos2A≥0(其中y>0).
因为△ABC为锐角三角形,所以y>0,cos2A>0,从而y≥8.当y=8时,上式变为
sin2A-8cosA·sinA+16cos2A=0,
即
(sinA-4cosA)2=0,
亦即tanA=4.故tanA·tanB·tanC的最小值是8,当且仅当tanA=4时等号成立.
方法3 (弦化切法)
下同解法5(略).
方法4 (均值不等式放缩法)由
得
故tanA·tanB·tanC的最小值为8.
方法5 (函数最值法)
不妨设sinA=t(其中0 3.3 转化与化归 根据题意,将三角形式的题目等价转化为代数问题,解决起来更方便快捷.由“查清结构”中的解题思路可将问题转化为如下的命题: 例2 已知实数x>0,y>0,z>0,满足y+z=2yz,x+y+z=xyz,则xyz的最小值是多少? 分析 对于多元最值问题,常常采用消元法,利用基本不等式与函数思想进行解题.消元是解决多变量问题的基本大法.消元的方式有2种:直接消元(代入消元和整体消元)和引参消元.该问题可以直接代入消元.由于篇幅原因,以下只列举2种方法,以供参考. 解法1 由条件得 x+2yz=xyz, 从而 于是 采用例1中的解法5或解法6,可求得xyz的最小值是8. 解法2 由条件y+z=2yz,得 由解法1知 从而 故 下同解法1. 4.1 重视数学思想,积累解题经验 在平时的数学学习中,多提炼例、习题中所蕴藏的数学思想.如本题中,涉及许多审题的视角(不等式、函数、等差中项和对偶构造)、数学思想(换元、化归与转化、数形结合)和数学方法(整体法、换元法、消元法、判别式法)等重要内容,内化为自己知识体系中的解题经验和微型模型,能够更好地提升思维水平和开发数学潜能. 4.2 关注“三审”过程,通达数学自觉 因此,解题时要多关注三审(审条件、审结论和审联系)环节,这样就能融会贯通数学的各个知识点,形成知识的系统化,解题时左右逢源、游刃有余. 第1步:选择函数f(x);第2步:构造数列{an}的通项an=k[f(n)-f(n-1)],并将an化简(不能化简的没有研究的必要);第3步:选定一个k值,生成裂项法求和问题. 说明:k取不同的值,可生成不同的求和问题. 通过1)的示范讲解,学生基本把握了裂项法求和问题的生成方法及裂项技巧.紧接着给学生10分钟自编自练,再给学生15分钟在小组内交换练习,教师巡视指导,最后剩下的时间以小组为单位通过投影仪展示各组的编题成果.现将各组展示的问题整理如下(限于篇幅,部分解答省略): 取k=1得到: an=f[f(n)-f(n+1)]= 取k=-1得到: 6)选择函数f(x)=x(x+1),计算 an=k[f(n)-f(n+1)]= k[n(n+1)-(n+1)(n+2)]= -2k(n+1). 问题6 已知数列{an}的通项an=n+1,求数列{an}的前n项和Sn. 7)选择函数f(x)=x(x+1)(x+2),计算 an=k[f(n)-f(n+1)]= k[n(n+1)(n+2)-(n+1)(n+2)(n+3)]= -3k(n+1)(n+2). 问题7 已知数列{an}的通项an=(n+1)(n+2),求数列{an}的前n项和Sn. 9)选择函数f(x)=qx-1(其中q≠0且q≠1),计算 an=k[f(n)-f(n+1)]=k(qn-1-qn)= k(1-q)qn-1. 问题9 已知数列{an}的通项an=a1qn-1,求数列{an}的前n项和Sn. 10)选择函数f(x)=tanx,计算 an=k[f(n)-f(n+1)]=k[tann-tan(n+1)]= 取k=-1得到: 11)选择函数f(x)=tan(2xα),计算 an=k[f(n)-f(n+1)]= k[tan(2nα)-tan(2n+1α)]= 取k=-1得到: 12)选择函数f(x)=cot(2xα),计算 an=k[f(n)-f(n+1)]= k[cot(2nα)-cot(2n+1α)]= 取k=-1得到: 1)苏霍姆林斯基说过:“在人的灵魂深处,都有一种根深蒂固的需要,就是希望感到自己是一个发现者、研究者、探索者.”[1]过去学生被动做题,缺乏学习的主动性,甚至会感到枯燥乏味.现在教会了学生用生成方法自编自练,交换练习,教师把学习的主动权还给了学生,让他们自己去发现问题、研究问题,极大地激发了学生的学习热情和学习兴趣,学生乐此不疲,就像玩游戏一样不断写出新的函数,不断生成新的求和问题.一系列新颖别致的求和问题给学生带来了快乐,带来了成功的感受和体验. 2)学生在编题过程中,使自己的思维品质得到了优化和提升,尤其是逆向思维能力得到了很好的锻炼;使他们看到了题目生成背后的故事,有利于抓住问题的本质特征,破译解题玄机,把握裂项法的规律和技巧,提升自己的解题能力. 3)学生通过编题,拓展了自己的思维空间.选择不同的函数编题,使所学的知识得到了联系和发展,使学生更能适应在知识的交汇点设置问题的考试要求.同时对数列中的函数思想也有了更为深刻的认识. 5)美国缅因州的国家训练实验室研究成果表明:课堂中,学生单纯的“听讲”,2周后所学知识的保持率仅为5%;通过“看”教师的示范演示,2周后也只能保持30%;而通过“小组讨论”获得的知识,2周后的保持率可达到50%;如果能在“做中学或实际演练”获得知识,2周后的保持率可达到70%;如果能够自己获得并“教别人”,保持率可达到90%[2].由此可见,合理放手,适度让位,教给学生裂项法求和问题的生成方法,让学生自编自练,互编互练,给学生自主探究、展示交流的空间,可大大提高所学知识的保持率,使课堂变得更加高效. [1] 张艳.一道例题体验三种角色[J].数学通报,2016(11):51-53. [2] 缪林.平面与平面垂直的判定教学片段及教学反思[J].数学通报,2012(7):22-24. 2016-11-24; 2016-12-30 宫前长(1964-),男,甘肃礼县人,中学高级教师.研究方向:数学教育. O122 A 1003-6407(2017)05-12-05
4 教学启示
1 裂项法求和问题的生成方法
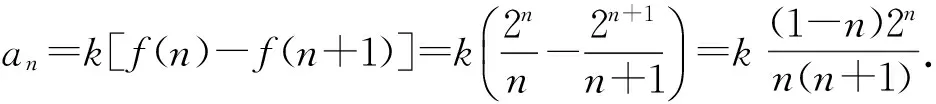
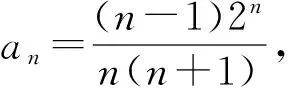
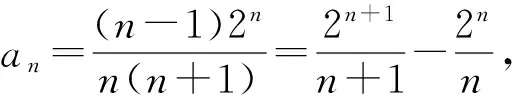
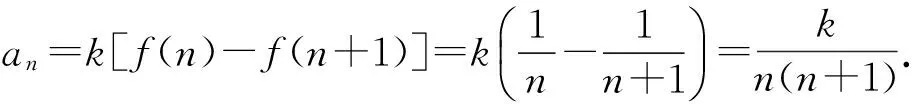
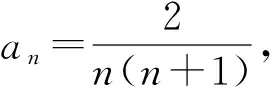
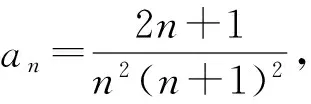
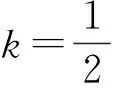
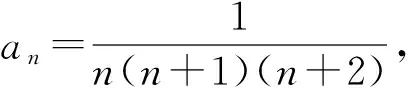
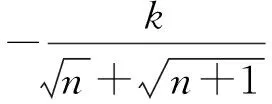
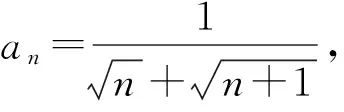
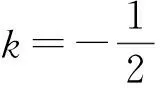
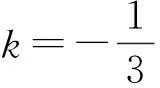
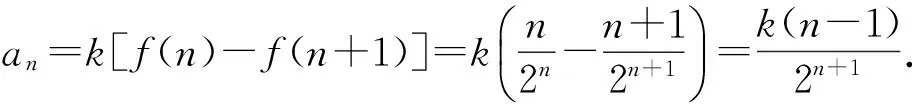
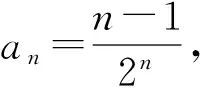
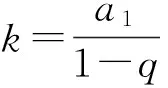
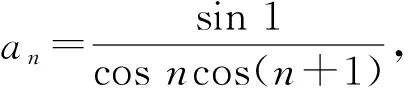
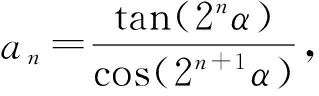
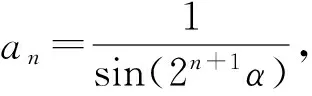
2 生成方法在教学中的作用