基于同步监测和深度学习的电容器介损角辨识

王晓辉，朱永利，郭丰娟

(华北电力大学控制与计算机工程学院，河北省保定市 071003)

基于同步监测和深度学习的电容器介损角辨识

王晓辉，朱永利，郭丰娟

(华北电力大学控制与计算机工程学院，河北省保定市 071003)

电容器在线监测系统中，不同位置监测装置受导线电流的干扰不同，因此工程中使用谐波分析法计算介损角存在不稳定问题。该文提出了一种基于同步监测和深度学习的电容器介损角辨识方法。首先给出了电容器电流、电压信号无线同步监测方法，以及用于深度学习的介损角表示信号Dδ(t)的计算过程。然后仿真验证方法的有效性并与基于加汉宁窗的谐波分析法进行比较。最后对深度神经网络隐含层进行了可视化分析，结果显示，该方法的正确率主要受噪声、谐波幅值比、介损角变化量等影响，且在谐波幅值比小于10%的情况下，辨识结果受频率偏移、谐波与基波相角差的影响较小。

深度学习；介损角；同步监测；电容器

0 引 言

电力电容器广泛应用于电力系统无功补偿，在运行中长时间承受工作电压和电流作用而逐渐老化，电力电容器的介质损耗因数(介质损耗角的正切值tanδ)是表征其质量的重要参数。对电容器进行在线监测可以及时发现电容器早期故障，监测效果好于定期检修方式[1-5]。在线监测方式计算精度除算法本身的精度外还容易受到多种外界干扰[6]，如电压相角的监测受电压互感器(potential transformer, PT)角差的影响[7-8]，电流相角的监测受电流互感器(current transformer, CT)角差的影响以及监测装置传感器受母线电流的干扰等。

适用于介损角在线监测的计算方式有谐波分析法、正交分解法、异频电源法等[9-19]。谐波分析法利用离散傅里叶变换(discrete fourier transform，DFT)对电容器的电压和电流信号进行谐波分析，得到两者的基波，从而计算介损角。该方法受频率波动影响较大，且存在非同步采样引起的频谱泄漏和栅栏效应[9-10]。为解决该问题，文献[11]提出了基于Blackman-Harris的DFT介损角测量方法，文献[12]提出了高阶正弦拟合算法，文献[13]提出了一种非同步采样条件下采用基波相位分离法的补偿算法，但未从根本上解决非同步采样的影响问题。文献[14-23]对谐波分析法做了不同程度的改进，并取得了一定的效果。正交分解方法不受过零点偏移的影响，所需的采样时间短，但该算法受电压频率波动影响较大[19]。

近年来深度学习受到越来越多的关注[24-29]，在电力系统信号分析领域取得了一定的应用成果[29]。本文提出一种基于深度学习的电容器介损角在线辨识方法。该方法不是从正向计算介损角，而是对每只电容器同步监测到的电流和电压信号做一定的预处理后，深度学习每只电容器监测信号的特征。再用训练完成的深度学习网络辨识新监测的信号属于解空间(介损角变化量级别)的哪个域，从而辨识介损角的变化量。实验表明本文方法在辨识精度、抗白噪声、频率偏移等方面优于谐波分析法。

1 基于无线传感网络的介损角同步在线监测

某变电站电容器组A相安装方式如图1所示。

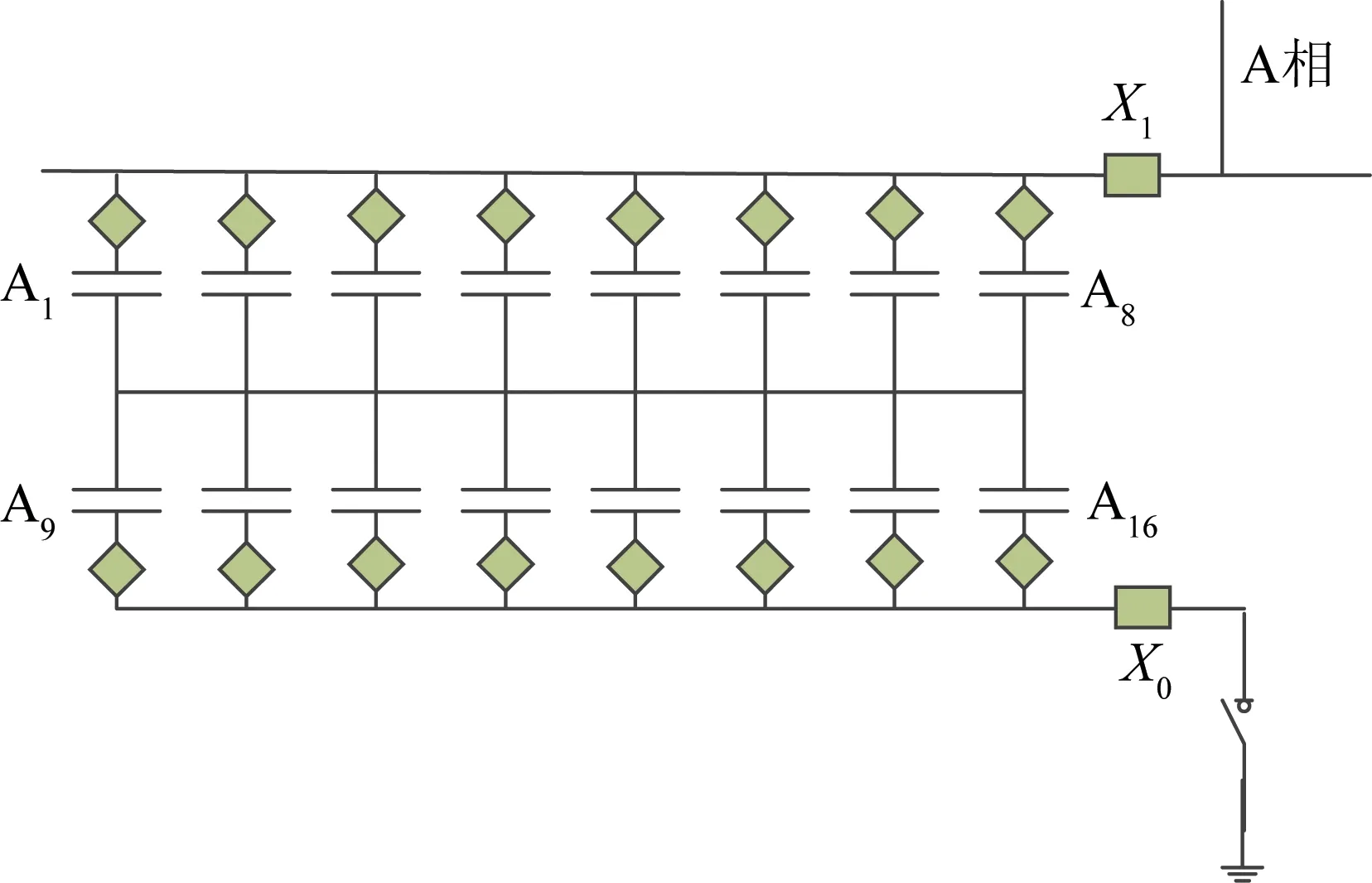
图1 电容器监测装置安装示意图Fig.1 Installation positions of capacitor monitoring devices

图1中矩形框X1点为连接A相的导线铝牌，X0点为三相的中性点，X1～X0间工作电压可以通过该相PT测定，各电容器工作电压、相位可通过电容串并联关系计算得到。

本文在线监测方法为：(1)在每只电容器外置保险丝处(图1菱形框位置)安装电流传感器，用以测量电容器电流。(2)在电容器所在相铝牌和中性点处(图1矩形框处)安装电流监测装置(CT监测点)，用以对各电流传感器信号进行同步采集和无线数据传输。(3)在电容器PT二次侧安装电压监测装置(PT监测点)，对电容器电压信号进行同步采集和无线传输。(4)在变电站值班室安装监控服务器，用以接收电流、电压采集数据，计算电容值、介损角等监测量。基于无线传感网络的电容器在线监测结构如图2所示。

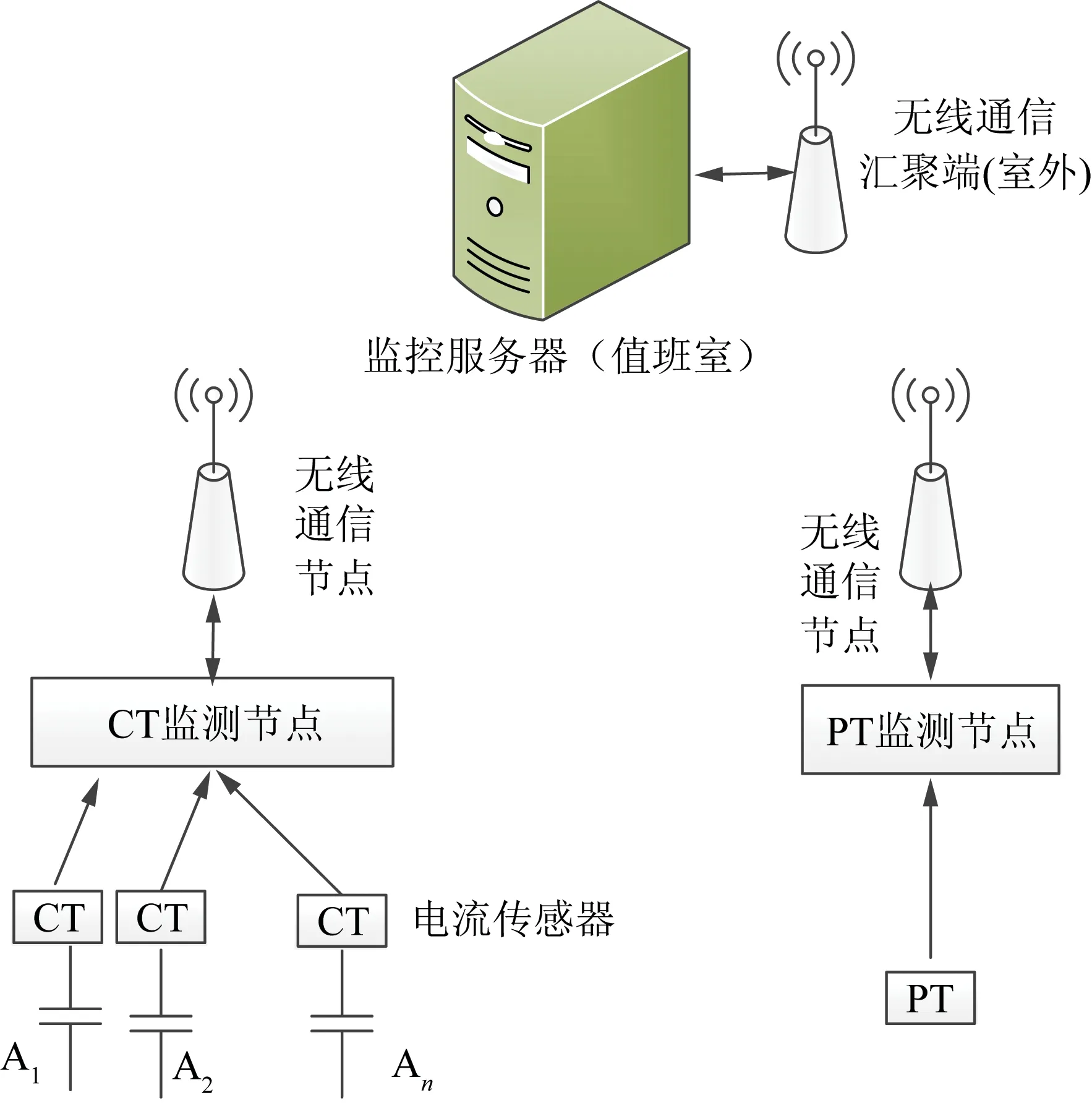
图2 基于无线传感网络电容器监测结构图Fig.2 Structure of capacitor monitoring system based on wireless sensing network

图2中A1～An是A相安装的并联电容器，CT为电流传感器。PT为电容器组电压传感器，将电容器工作电压转换为100 V交流电压。

CT监测点和PT监测点为基于无线传感网络的监测节点，该节点装有本文改进型Zigbee无线通信模块(限于篇幅另外叙述)，可以在220 kV高压环境下可靠传输数据。监控服务器安装在变电站值班室内，配有Zigbee通信模块，并与CT、PT监测节点组网。在线监测系统利用高精度GPS授时模块(同步误差均方差为30 ns)定期每5 min对电容器电流、电压进行采集，采样频率为10 kHz、采样时长80 ms，采样信号传回服务器后进一步对其进行谐波分析、深度学习辨识等，从而完成对电容器组的状态评估。

在基于加汉宁窗的谐波分析法计算介损角模块中，积累3个月的监测数据后发现介损角值计算不稳定。例如A相1号电容器介损角的介损角核密度如图3所示(样本数为1 497)。

图3 A相1号电容器介损角核密度Fig. 3 Density plot of tan(δ) for capacitor A1

从图3中可以看出，在线监测值大部分与离线检测值0.3×10-3rad相近，但一些监测值偏移量较大。通过对偏移监测信号的分析发现电容器电流的监测波形出现不同程度的畸变。常见的电力电容器的工作电流为28～50 A，每相安装8～16只电容器时，母线的电流约为224～800 A，对电容器监测装置和传感器形成较大的磁场干扰。通过对在线监测数据的分析发现，单只电容器工作电流传感器受母线电磁场的干扰相对稳定，不同位置的传感器所受的干扰不同，在线监测系统需要对每只电容器监测装置受到的干扰分别进行处理。传统的介损角计算方法不能区别单只电容器受到的干扰，因此计算值存在不稳定现象。

深度学习具有多层非线性映射的深层结构，可以完成复杂的函数逼近，因此深度学习方法可以辨识每只电容器受到的干扰信号，从而提高介损角计算精度。

用于分类的神经网络有BP神经网络(back-propagation artificial neural network)、卷积神经网络、深度前馈多层神经网络等。经过比较：卷积神经网络精度最高、但训练速度最慢；BP神经网络和深度前馈多层神经网络训练速度相当，但BP神经网络辨识本文样本精度不高。在电容器在线监测系统中，深度前馈多层神经网络训练速度较快，且精度满足实际工程需要。

2 用于深度学习的介损角信号Dδ(t)

本文使用如下方法将在线监测到的电流、电压信号转换为可表示介损角δ的信号Dδ(t)。

使用U(t)和I(t)描述电容器的工作电压和电流：

U(t)=AUsin(ωt+φU)

(1)

I(t)=AIsin(ωt+φI)

(2)

式中：AU为电压幅值；ω为角频率；φU为电压初始相角；AI为电流幅值；φI为电流初始相角。

在同步采样方式下，介损角δ的计算主要依据U(t)和I(t)的相位差，可不考虑其幅值。为方便讨论问题，将采样信号U(t)和I(t)的幅值归一化为1，且同时移相φI使I(t)初始相角为0，则U(t)和I(t)退化为无量纲的信号U～(t)和I～(t)。

U～(t)=sinωt+(φU-φI)

(3)

I～(t)=sin(ωt)

(4)

将信号U～(t)沿x轴前移π/2得到U～s(t)。

U～s(t)=sin[ωt+(φU-φI)-π/2]=sin(ωt-δ)

(5)

从式(4)、(5)可以看出，U～s(t)和I～(t)信号相位差为待计算的介损角δ。定义信号Dδ(t)为

Dδ(t)=U～s(t)-I～(t)=-2sin(δ2)cos(ωt-π2)

(6)

由式(6)可见，Dδ(t)的角频率与电容器电流、电压相同，Dδ(t)的幅值与被测的介损角δ有关。

定义Dδ(t)信号幅值的绝对值为Aδ，则Aδ=2sin(δ/2)，设Aδ与δ的比值为R(δ)。

R(δ)=Aδδ=2sin(δ/2)δ=sin(δ/2)δ/2

(7)

高压并联电容器在额定电压下，20 ℃时介损角δ应符合下列值：纸膜复合介质的电容器应不大于0.8×10-3rad；全膜介质的电容器中，有放电电阻和内熔丝的应不大于0.5×10-3rad，无放电电阻和内熔丝的应不大于0.3×10-3rad。由式(7)可见，当0<δ<0.8×10-3rad时，R(δ)的值为[0.999 999 9,1.000 000 0]。因此在讨论域内，Dδ(t)信号的幅值的绝对值Aδ等效于介损角δ的值。将介损角δ的测量从电压、电流相位差的计算转换为Dδ(t)信号幅值和形状的比较，并以此作为深度学习的输入信号。

3 基于深度学习的Dδ(t)信号辨识方法

基于深度学习的介损角δ辨识过程是一种解空间搜索过程。其核心思想是使用每只电容器一段时间的Dδ(t)来训练相应电容器的深度学习网络，使深度网络可以辨识其介损角值以及受到的相对稳定的电流干扰，这一过程耗时较长。再使用该深度学习网络辨识新监测到的Dδ(t)信号是否为期望的δ，还是偏移了一定量的δi，该过程计算速度快，可用于在线监测，该过程可用图4表示。

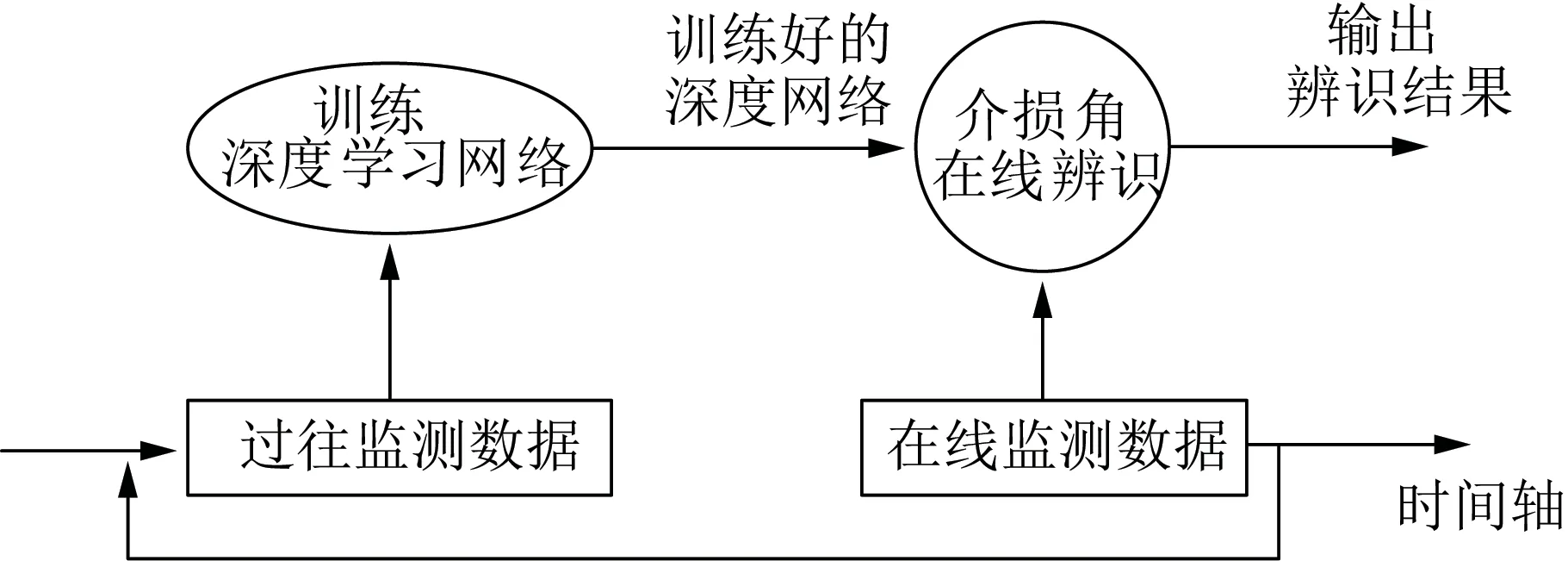
图4 基于深度学习的介损角辨识过程Fig.4 Dielectric loss angle identification procedure based on deep learning network

图4中，深度学习网络的隐含层可选“平层”型和“瓶颈”型网络，两者训练时间、辨识精度相当，但“瓶颈”型网络中间层易对分类结果做可视化分析。本文选择“瓶颈”型隐含层的深度前馈多层神经网络，该网络采用Dδ(t)信号集作为输入，介损角变化量作为输出。本文监测系统参数为：(1)目标电容器的介损角δ0为0.3×10-3rad；(2)在线监测系统的采样率为10 kHz；(3)每次同步采集4个周期，采样点数为1 600，因此输入层为1 600；(4)隐含层设计为(400,200,3,200,400)的5层瓶颈(bottle-neck)网络；(5)输出层为介损角值依次增加10次0.001%的离散类。

仿真过程：

(1)使用Matlab生成介损角δi为{0.30×10-3，0.31×10-3，0.32×10-3，…，0.39×10-3，0.40×10-3}rad、频率分别为{49.50,49.75,50.00,50.25,50.50}Hz条件下的介损角信号Dδi(t)集。

(2)对Dδi(t)按下列条件增加谐波：1)谐波次数为3、5、7；2)各次谐波的初始相角与基波相角差为{-π/3,π,π/3}；3)各次谐波的幅值为基波幅值的{0,5%,10%}。

(3)所有样本加{20,25,30,35}dB 4个等级的白噪声，每个噪声等级生成10个加噪信号作为训练集TrainSet。

(4)在构建TrainSet算法的基础上按照下列条件构造测试集TestSet：1)对各次谐波相角增加-π/6至π/6之间随机的漂移；2)介损角增加-0.5×10-6至5×10-6rad之间的随机漂移；3)频率增加-0.25至0.25 Hz之间的随机漂移。每个测试样本加{20,25,30,35}dB 4个等级的白噪声，每个噪声等级生成5个加噪信号。

(5)使用隐含层为(400,200,3,200,400)、激活函数为Rectifier(如图5所示)、迭代次数为100的深度学习网络以δi为分类依据进行训练。

(6)使用TestSet检验深度学习网络在不同δi下的Dδi(t)信号的辨识能力。

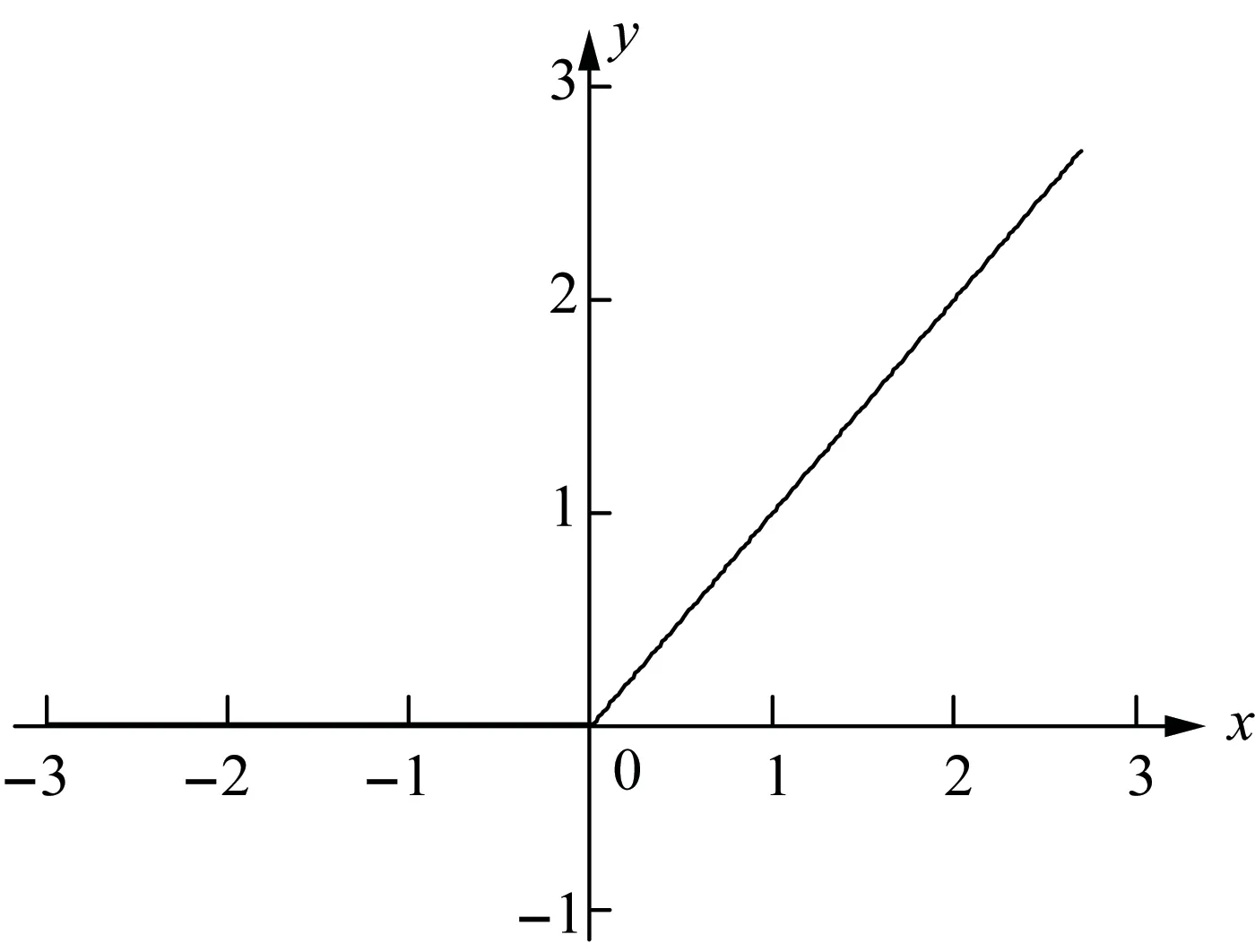
图5 Rectifier激活函数Fig.5 Curve of Rectifier activation function

训练过程中深度学习网络的均方差(mean square error,MSE)趋势如图6所示。

图6 深度学习网络学习过程中均方差图Fig.6 Mean square deviation of deep earning procedure

从图6可以看出，当迭代次数为55～60次时，深度学习网络的MSE已经小于设定阈值1×10-10，训练结束。

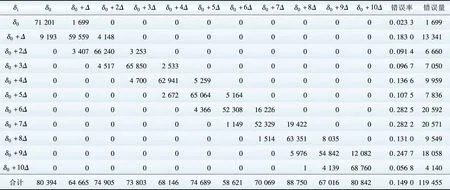
使用测试数据集TestSet检验深度学习网络在不同δi时测试信号的分类能力，其分类情况如表1所示，表中δ0=0.30×10-3rad，Δ=0.01×10-3rad。

仿真过程中δi生成的训练样本为1 603 800条，测试数据集TestSet样本总量为801 900条。从表1可见，在基波中增加谐波、频率偏移和白噪声的条件下，深度学习网络辨识介损角变化10个Δ的总体错误率为14.9%，最大误差不超过±Δ，该误差比介损角小一个数量级，满足实际工程需要。

仿真结果表明信号加入20 dB的白噪声信号时，本方法仍然可以辨识介损角变化量，优于基于加汉宁窗插值的谐波分析法中白噪声大于35 dB的要求[18]。

表1 深度学习网络对于电容器介损角测试数据集的辨识结果

Table 1 Dielectric loss angle identification results on test dataset of a capacitor by proposed deep learning network

4 辨识结果分析

基于深度学习的介损角辨识方法本质是信号分类问题。即通过仿真计算介损角依次变大若干Δ，且样本中混入谐波、频率偏移、白噪声的情况下，深度神经网络能否区分每个Δ的变化。本文使用的深度神经网络隐含层为(400,200,3,200,400)，是一种典型的瓶颈(bottle-neck)网络，可以利用第3层数据作为三维坐标，从而图形化展示分类情况，使用介损角变化量Δ作为着色条件，第3节实验分类结果如图7所示。

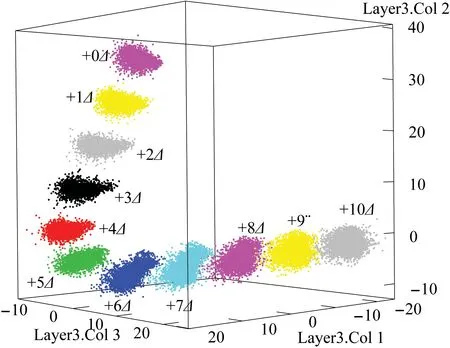
图7 基于深度学习的介损角辨识图Fig.7 Dielectric loss angle identification based on deep learning

从图7可以看出，当介损角增加0～5个Δ时分类较为清晰，但增加6Δ以上时分类界限模糊。

使用辨识是否正确作为着色条件时的分类图如图8所示。

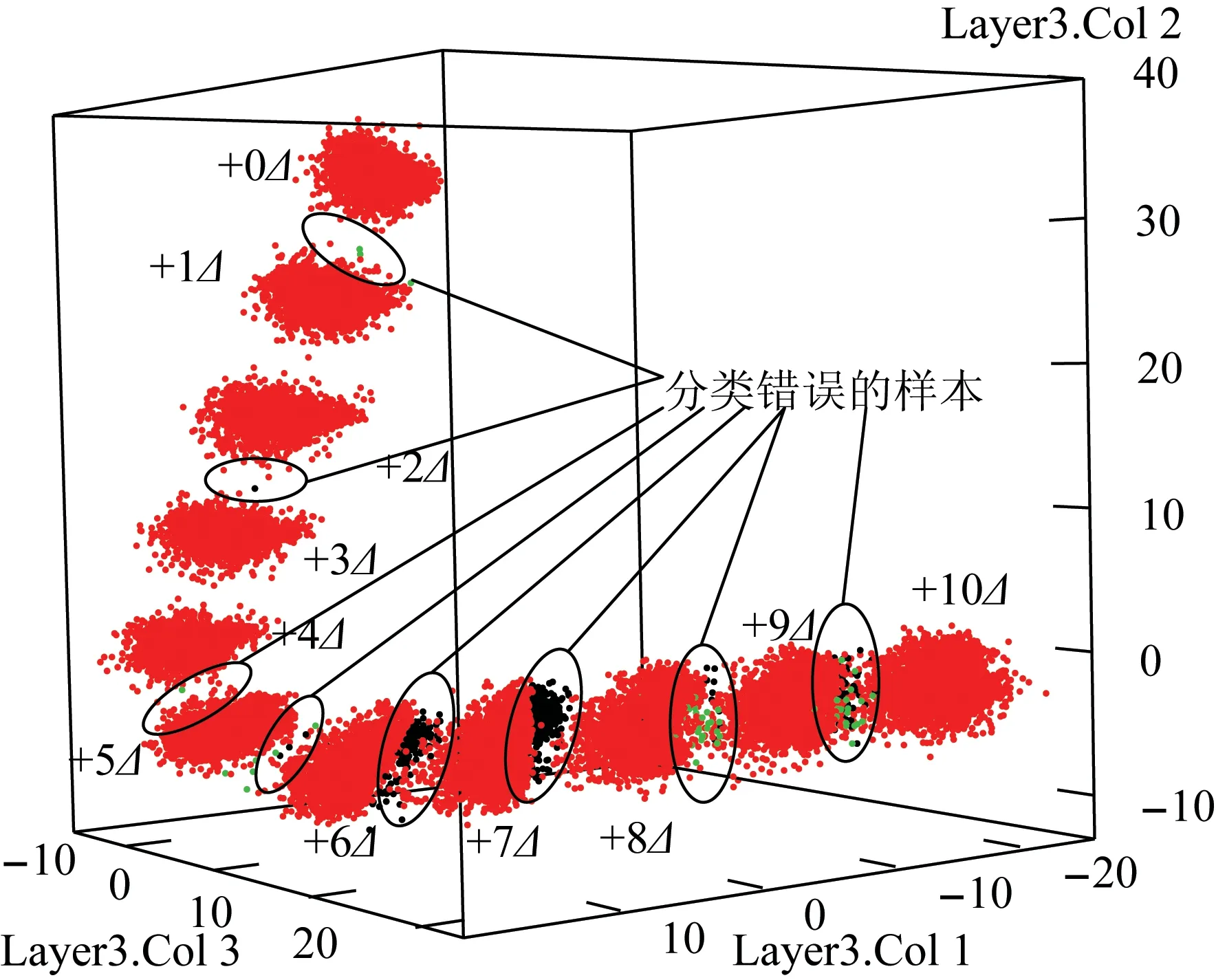
图8 辨识结果中错误样本的分布图Fig.8 Scattergram of error samples in identification results

由图8中可知，辨识错误样本主要分布在介损角增加6Δ后的类别中。在分类错误的样本中，使用统计方法判断的介损角值、各次谐波幅值、各次谐波相角、频率偏移和白噪声分布情况，从而找出影响辨识结果的因数。

4.1 白噪声对辨识结果的影响

在辨识错误的样本中，按不同噪声等级统计介损角变化情况如图9所示。

从图9中可以看出，在白噪声为20 dB时辨识错误的样本数最多，且约26.4%的样本被辨识为小了一个Δ。白噪声为25，30，35 dB情况下相近，介损角被辨识减小Δ的比例为0.87%，绝大多数的情况被辨识为增加了一个Δ。白噪声为35 dB时的测试集TestSet的辨识分类图如图10所示。

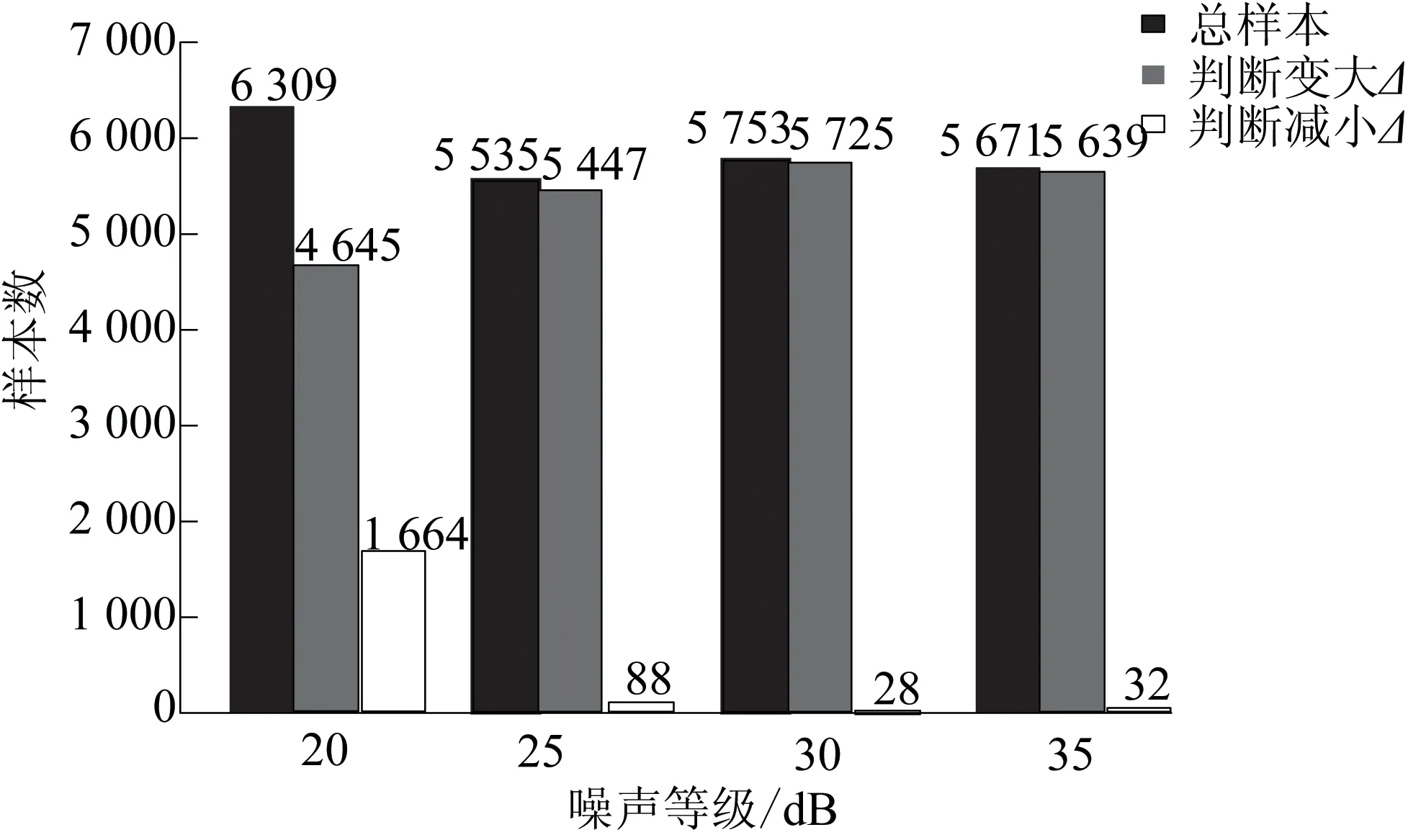
图9 辨识错误样本集中不同噪声等级分布情况Fig.9 Distribution of different noise levels of identification error sample set

图10 白噪声为35 dB时的分类情况Fig.10 Classification diagram when white noise is 35 dB

从图10可以看出，当噪声等级为35 dB时深度学习网络可以准确地区分介损角的变化量。可见白噪声对深度学习辨识结果有较大影响。

4.2 介损角变化量对辨识结果的影响

在分类错误的样本中，统计介损角变化不同Δ时的辨识能力，辨识结果如图11所示。

从图11可以看出介损角增加6Δ以上时，辨识错误率明显增加，说明介损角增加量对基于深度学习的辨识结果有一定的影响。

4.3 频率偏移对分类结果的影响

在分类错误的样本中，统计不同频率偏移条件下的样本分布情况，统计结果如图12所示。

从图12可以看出，当频率减小0.25 Hz和增加0.25 Hz时本文方法分类错误率较高，但错误样本量在同一个数量级。

4.4 各次谐波的幅值和相角对分类结果的影响

在分类错误的样本中，统计各次谐波幅值含量(百分比)不同时的辨识能力。本文仿真了3、5、7次谐波幅值含量分别为0%、5%、10%时的组合情况，统计结果如图13所示。

图11 辨识错误样本集中不同介损角变化量分布情况Fig.11 Histogram of error samples group by level of dielectric loss angle variation

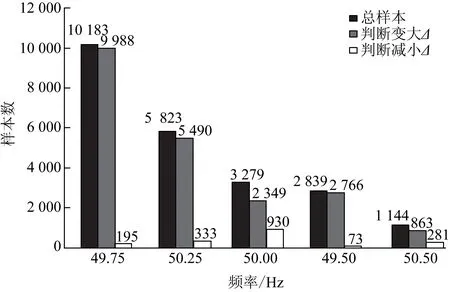
图12 辨识错误样本集中不同频率分布情况Fig.12 Histogram of error samples group by frequency deviation level

从图13可以看出，当3、5、7次谐波幅值含量都为5%时错误率最高，且错误率最高的前4位3次谐波的幅值含量为5%，且样本数超出其他组合一个数量级。

辨识错误样本中，各次谐波与信号的相角差组合分布情况如图14所示。

从图14中可以看出辨识错误样本中相角差组合分布较为均匀，各次谐波与信号起始相角相同时辨识错误样本较多。

5 结 论

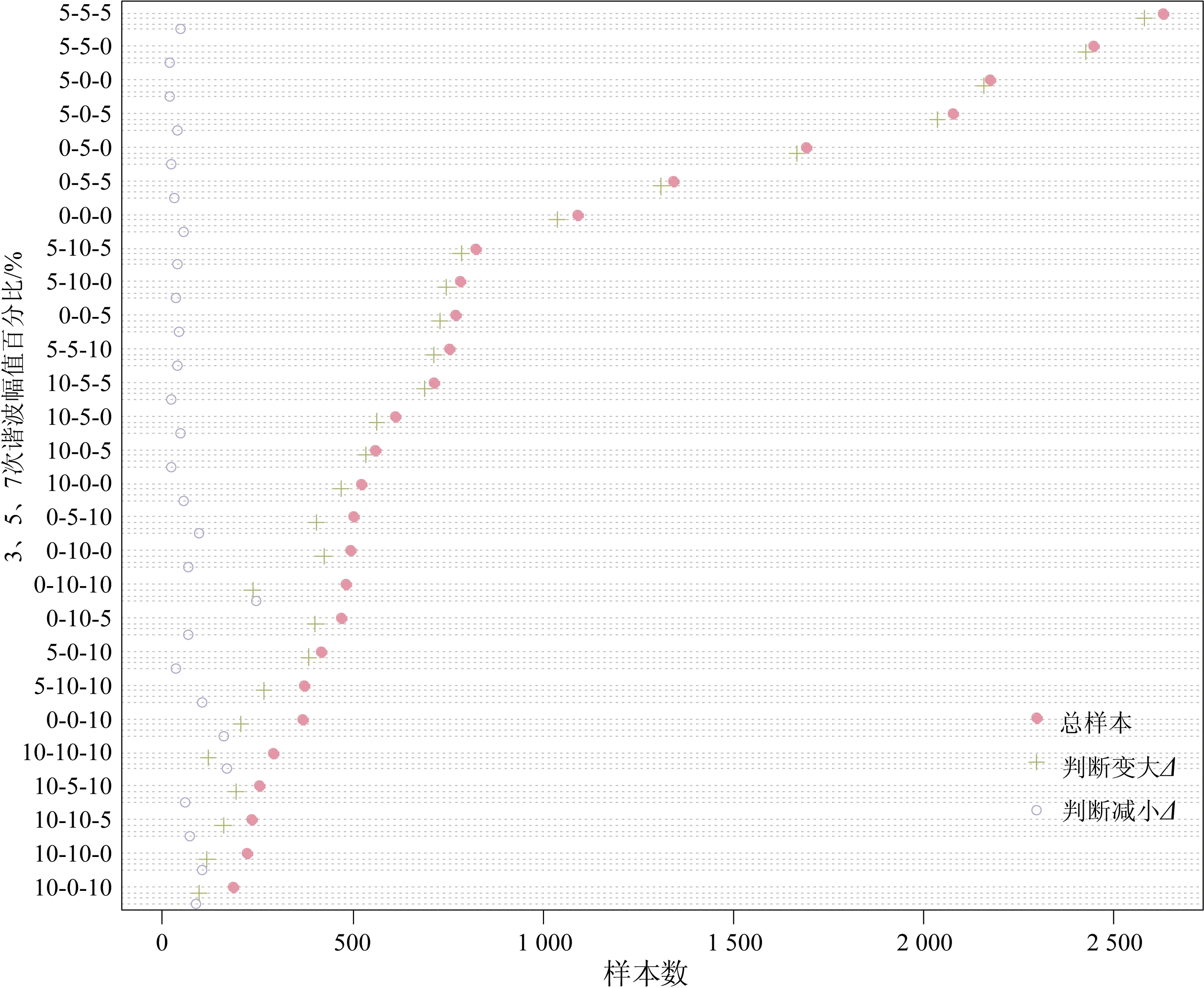
图13 辨识错误样本集中谐波幅值组合分布情况Fig.13 Dot plot of error samples group by harmonics amplitude ratio combination

图14 辨识错误样本集中各次谐波相角差分布情况Fig.14 Dot plot of error samples group by phase difference combination of harmonics

以谐波分析法为代表的介损角计算方法在实际监测项目中稳定性不佳。本文提出了一种介损角表示信号Dδ(t)，并使用该信号作为输入实现了基于深度学习的介损角辨识方法。实验表明：

(1)本文方法辨识结果准确，且误差不会大于±1×10-6rad，训练速度较快，适用于在线监测；

(2)本文方法抗噪性能优于基于汉宁窗的谐波分析法；

(3)本文方法辨识准确性受白噪声等级、介损角变化量、谐波幅值的影响较大，受频率偏移、谐波相角差组合影响较小。受频率偏移影响方面辨识效果优于谐波分析法。

[1] 董爽, 李天云, 王永,等. 在线检测介质损耗角的矩阵束方法[J]. 电工技术学报, 2015, 30(18):229-236. DONG Shuang, LI Tianyun, WANG Yong, et al. An on-line detection method of dielectric loss angle based on matrix pencil algorithm[J]. Transactions of China Electrotechnical Society, 2015, 30(18):229-236..

[2] WANG P， RAGHUVEER M R， MCDERMID W， et al． A digital technique forthe online measurement of dissipation factor and capacitance[J]． IEEE Transactions on Dielectric Electrical Insulation， 2001， 8(2)： 228-232.

[3] 尚勇, 杨敏中, 王晓蓉,等. 谐波分析法介质损耗因数测量的误差分析[J]. 电工技术学报, 2002, 17(3):67-71. SHANG Yong, YANG Minzhong, WANG Xiaorong, et al. Error analysis for the dielectric loss factor measurement based on harmonic analysis[J]. Transactions of China Electrotechnical Society, 2002, 17(3):67-71.

[4] 刘伟,黄新波，章云. 电容型高压设备介损在线监测系统的现场采集单元设计[J]. 计算机测量与控制，2010,18(1)：233-242. LIU Wei, HUANG Xinbo, ZHANG Yun. Design of field sampling unit of an on-line monitoring system of dielectric loss in capacitive high-voltage apparatus[J]. Computer Measurement & Control,2010,18(1)：233-242.

[5] 陈晓宇, 郑建勇, 梅军. 基于LC振荡频率变化量的电容器组早期故障在线智能预警方法及其实现[J]. 电力系统保护与控制, 2015, 43(5):144-149. CHEN Xiaoyu, ZHENG Jianyong, MEI Jun. Power capacitor banks failure warning method based online intelligence LC oscillation frequency variation and its implementation[J]. Power System Protection & Control, 2015, 43(5):144-149.

[6] 徐志钮, 律方成, 李和明. 采样时间和采样频率对基于加窗插值算法介损角测量的影响[J]. 华北电力大学学报(自然科学版), 2007, 34(4):7-10. XU Zhiniu, LV Fangcheng, LI Heming. Influence of sampling time and sampling frequency on dielectric loss angle measurement based on windowed interpolation algorithm[J]. Journal of North China Electric Power University(Natural Science Edition), 2007, 34(4)7-10.

[7] 谢华, 张会平. 电压互感器角差对介损在线监测的影响分析[J]. 高电压技术, 2003, 29(5):26-28. XIE Hua, ZHANG Huiping. The influence of angle error of cvt on on-line tanδmonitoring[J]. High Voltage Engineering, 2003, 29(5):26-28.

[8] 李振华, 李红斌, 张秋雁,等. 一种高压电子式电流互感器在线校验系统[J]. 电工技术学报, 2014, 29(7):229-236. LI Zhenhua, LI Hongbin, ZHANG Qiuyan, et al. An online calibration system for high voltage electronic current transformers[J]. Transactions of China Electrotechnical Society, 2014, 29(7):229-236.

[9] 蔡国雄，甄为红，杨晓洪，等．测量介质损耗的数字化过零点电压比较法[J]．电网技术， 2002，27(7)：15-18． CAI Guoxiong, ZHEN Weihong, YANG Xiaohong, et al. A digitized zero cross point voltage method of comparison for measurement of dielectric losses[J]. Power System Technology, 2002, 26(7):15-18.

[10] 袁飞, 杨震男, 卢毅. 一种基于相对比较法测量容性设备介质损耗的滤波算法[J]. 电力系统保护与控制, 2015, 43(19):95-100. YUAN Fei, YANG Zhennan, LU Yi. A filtering algorithm for measuring capacitive device dielectric loss based on relative comparison method[J]. Power System Protection & Control, 2015, 43(19):95-100.

[11] 王楠，律方成，梁英，等．基于高精度 DFT 的介损数字测量方法[J]．高电压技术，2003， 29(4)：3-8. WANG Nan, LV Fangcheng, LIANG Ying, et al. Digital measurement of dielectric loss based on high accuracy DFT algorithm[J]. High Voltage Engineering, 2003, 29(4)：3-8.

[12] 王徽乐，李福祺，谈克雄．测量介质损耗角的高阶正弦拟合算法[J]. 清华大学学报(自然科学版)，2001，41(9)：5-8. WANG Weile, LI Fuqi, TAN Kexiong. Higher-order sine fitting algorithm for dielectric loss measurement[J]. Journal of Tsinghua University(Science & Technology), 2001,41(9)：5-8.

[13] 陈楷，胡志坚，王卉，等．介损角的非同步采样算法及其应用[J]．电网技术，2004，28(18)：58-61. CHEN Kai, HU Zhijian, WANG Hui, et al. Algorithm and application of dielectric loss angle based on asynchronous sampling[J]. Power System Technology, 2004, 28(18):58-61.

[14] 冯小华，张承学．修正的谐波分析法可提高介损在线测量准确度[J]．高电压技术，2004，30(8)：36-37． FENG Xiaohua, ZHANG Chengxue. Modified harmonics analysis approach for increasing precision in on-line measuring tanδ[J]. High Voltage Engineering, 2004，30(8)：36-37.

[15] LI Q，ZHAO T，SIEW W H．Definition and digital algorithms ofdielectric loss factor for condition monitoring of high-voltage powerequipment with harmonics emphasis[J] ． IEEE Proceedings on Generation，Transmission and Distribution，2005，152(3)：309-312.

[16] 张忠蕾，李庆民，陈鹏．谐波条件下高压电气设备介质损耗因数的定义和数字化算法[J]．高压电器，2004，40(5)：327-332． ZHANG Zhonglei, LI Qingmin, CHEN Peng. Definition and digital algorithms for dielectric loss factor of high voltage power apparatus under harmonics condition[J]. High Voltage Apparatus, 2004,40(5)：327-332.

[17] 张介秋, 梁昌洪, 韩峰岩,等. 介质损耗因数的卷积窗加权算法[J]. 电工技术学报, 2005, 20(3):100-104. ZHANG Jieqiu, LIANG Changhong, HAN Fengyan, et al. Convolution window weighted algorithm for dielectric loss factor[J]. Transactions of China Electrotechnical Society, 2005,20(3):100-104.

[18] 徐志钮, 律方成, 赵丽娟. 基于加汉宁窗插值的谐波分析法用于介损角测量的分析[J]. 电力系统自动化, 2006, 30(2):81-85. XU Zhiniu,LV Fangcheng， ZHAO Lijuan. Analysis of dielectric loss angle measurement by hanning windowing interpolation algorithm based on FFT[J]. Automation of Electric Power Systems, 2006, 30(2):81-85.

[19] 段大鹏,江秀臣, 孙才新, 等．基于正交分解的介质损耗因数数字测量算法[J]．中国电机工程学报, 2008, 28(7): 127-133. DUAN Dapeng, JIANG Xiuchen, SUN Caixin, et al. A novel algorithm of dielectric loss measurement based on orthogonal decomposition[J]. Proceedings of the CSEE, 2008, 28(7): 127-133..

[20] 温和, 滕召胜, 王一,等. 基于三角自卷积窗的介损角高精度测量算法[J]. 电工技术学报, 2009, 24(3):203-208. WEN He, TENG Zhaosheng, WANG Yi, et al. High accuracy dielectric loss angle measurement algorithm based on triangular self-convolution window[J]. Transactions of China Electrotechnical Society, 2009, 24(3):203-208.

[21] 李天云, 祝磊, 康玉芳,等. 基于总体最小二乘-旋转矢量不变技术的介损角测量算法[J]. 电网技术, 2009, 33(18):171-175. LI Tianyun, ZHU Lei, KANG Yufang, et al. Dielectric loss angle measurement algorithm based on TLS-ESPRIT[J]. Power System Technology, 2009, 33(18):171-175.

[22] 曾博, 唐求, 卿柏元,等. 基于Nuttall自卷积窗的改进FFT谱分析方法[J]. 电工技术学报, 2014, 29(7):59-65. ZENG Bo, TANG Qiu, QING Baiyuan, et al. Spectral analysis method based on improved FFT by nuttall self-convolution window[J]. Transactions of China Electrotechnical Society, 2014, 29(7):59-65.

[23] 黄冬梅, 龚仁喜, 焦凤昌,等. 莱夫-文森特窗三谱线插值的电力谐波分析[J]. 电力系统保护与控制, 2014,42(2):28-34. HUANG Dongmei, GONG Renxi, JIAO Fengchang, et al. Power harmonic analysis based on Rife-Vincent window and triple-spectral-line interpolation[J]. Power System Protection & Control, 2014, 42(2):28-34.

[24] 余凯, 贾磊, 陈雨强,等. 深度学习的昨天、今天和明天[J]. 计算机研究与发展, 2013, 50(9):1799-1804. YU Kai, JIA Lei, CHEN Yuqiang, et al. Deep learning:Yesterday,today,and tomorrow[J]. Journal of Computer Research & Development, 2013, 50(9):1799-1804.

[25] 孙志军, 薛磊, 许阳明,等. 深度学习研究综述[J]. 计算机应用研究, 2012, 29(8):2806-2810. SUN Zhijun, XUE Lei, XU Yangming, et al. Overview of deep learning[J]. Application Research of Computers, 2012， 29(8):2806-2810.

[26] 胡洋. 基于马尔可夫链蒙特卡罗方法的RBM学习算法改进[D]. 上海：上海交通大学, 2012. HU Yang . Markov chain monte carlo based improvements to the learning algorithm of restricted boltzmann machines[D].Shanghai: Shanghai Jiaotong University, 2012.

[27] CHEN Y, ZHAO X, JIA X. Spectral-spatial classification of hyperspectral data based on deep belief network[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(6):1-12.

[28] 李岳云, 许悦雷, 马时平,等. 深度卷积神经网络的显著性检测[J]. 中国图象图形学报, 2016, 21(1):53-59. LI Yueyun, XU Yuelei, MA Shiping, et al. Saliency detection based on deep convolutional neural network[J]. Journal of Image & Graphics, 2016, 21(1):53-59.

[29] 林颖, 郭志红, 陈玉峰. 基于卷积递归网络的电流互感器红外故障图像诊断[J]. 电力系统保护与控制, 2015，43(16):87-94. LIN Ying, GUO Zhihong, CHEN Yufeng. Convolutional-recursive network based current transformer infrared fault image diagnosis[J]. Power System Protection & Control, 2015，43(16):87-94.

郭丰娟 (1980)，女，硕士研究生，研究方向为电力系统自动化、机器学习等。

(编辑 张小飞)

Dielectric Loss Angle Identification of Capacitor Based on Synchronous Monitoring and Deep Learning

WANG Xiaohui, ZHU Yongli,GUO Fengjuan

(School of Control and Computer Engineering, North China Electric Power University, Baoding 071003, Hebei Province, China)

In the capacitor online monitoring system,the disturbance of lines on different position monitoring device is different. Therefor, the use of harmonic analysis in the calculation of dielectric loss angle has instability problem in engineering. This paper proposes a capacitor dielectric loss angle identification algorithm based on the synchronous monitoring and deep learning. Firstly, we present the wireless synchronous monitoring method of capacitor current and voltage signal, and the computation process of dielectric loss angle identification signalDδ(t) for deep learning. Then, we verify the effectiveness of the proposed method through simulation, and compare the results with the Hanning windowed harmonic analysis method. Finally, we analyze the visualization of deep neural networks hidden layer. The results show that the algorithm accuracy is affected by white-noise level, harmonic amplitude ratio and the variation level of dielectric loss angle. In situations when harmonic amplitude ratio less then 10%, the algorithm accuracy has been fewer affected by frequency deviation, phase difference of harmonics.

deep learning; dielectric loss angle; synchronous monitoring; capacitor

国家自然科学基金项目(51677072；51407076)；中央高校基本科研业务专项资金(2014MS131)资助

TM 835.4

A

1000-7229(2017)05-0076-09

10.3969/j.issn.1000-7229.2017.05.010

2017-02-25

王晓辉(1981)，男，博士研究生，研究方向为电力系统自动化、深度学习等；

朱永利(1963)，男，教授，博士生导师，研究方向为网络化监控和智能信息处理；

Project supported by National Natural Science Foundation of China(51677072；51407076); Fundamental Research Funds for the Central Universities(2014MS131)