区间集上非交换剩余格的广义模糊布尔滤子

罗俊丽

（商洛学院 数学与计算机应用学院，陕西商洛 726000）

美国数学家Zadeh于1965年首次提出的模糊集理论[1]，极大地促进了模糊逻辑推理系统和模糊逻辑代数分析两个重要研究方向的迅猛发展。Rosenfeld[2]受代数结构模糊化的启示，提出了模糊子群的概念，从而开创了模糊代数学研究的新领域。Bhakat和Das运用模糊点与模糊集间的“属于关系（∈）”和“拟重于关系（q）”[3-4],研究了（∈,∈∨q）-模糊子群的概念及性质[5-7]。张成讨论了（∈',∈'∨q'）-模糊子群的概念[8]；袁学海在引入模糊子群定义的基础上，得到了称之为模糊子群[9-10]的新模糊子群。廖祖华将Rosenfeld意义下的（∈，∈∨q）-模糊子群、Bhakat和Das意义下的-模糊子群以及袁学海意义下的模糊代数统一推广为（∈，∈∨q（λ，μ））-模糊代数[11],并获得了丰硕的成果。

本文是在Yao区间集[12-14]和滤子理论[15-20]研究工作的基础上,作为文献[21]研究讨论的继续，进一步将区间集和滤子理论运用到非交换剩余格上,引入区间集非交换剩余格广义模糊布尔滤子的概念，给出了区间集上非交换剩余格广义模糊布尔滤子的等价性刻画及其特征性质。

1 预备知识

定义 1[18]设＜I(2U),∪,∩,⊗,⇒,→,μ,Ø＞是一个（2，2，2，2，2，0，0）型代数，若满足以下条件：

1）＜I(2U)∪,∩，μ，Ø＞是一个有界格；

2) ＜I(2U)⊗,μ，Ø＞是 μ 以为单位元的半群；

3) ∀X，Y，Z∈I(2U)，X⊗Y⊆Z 当且仅当 X⊆Y⇒Z当且仅当Y⊆X→Z，则称I(2U)为区间集上非交换剩余格。

性质1[18]设I(2U)是一个区间集上非交换剩余格,∀X，Y，Z∈I(2U),则有以下性质成立：

1）⇒(→)：I(2U)×I(2U)→I(2U)关于第二个变量不减,关于第一个变量不增；

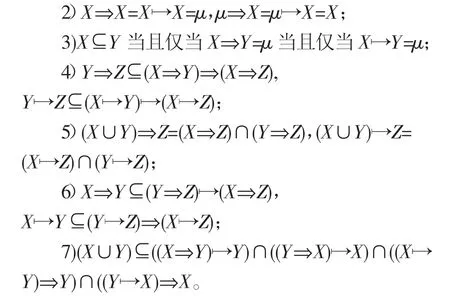
定义2[18]设I(2U)是区间集上非交换剩余格,F⊆I(2U),F≠μ 如果∀X，Y∈I(2U)，有

那么称F为I(2U)上的一个滤子，所有滤子之集记为F(I(2U))。

又若F是I(2U)的一个滤子,且满足∀X，Y∈I(2U),X∪Y⊆F可推出X⊆F或Y⊆F,则称F是I(2U)的素滤子。

命题1[18]设I(2U)是区间集上非交换剩余格,F⊆I(2U),F≠Ø,则F是滤子当且仅当F满足：

1）μ∈F；

2）若 X∈F,X⇒Y∈F 或者 X→Y∈F,则 Y∈F。定义3[18]设I(2U)是区间集上非交换剩余格,F：I(2U)→[Ø，μ]是一个映射，则 F 为 I(2U)的模糊子集。

定义4[18]设I(2U)是区间集上非交换剩余格,∀X，Y∈I(2U),F∈F(I(2U)),如果F满足以下条件：

1）若 X⊆Y,则 F(Y)⊇F(X)；

2）F(X⊗Y)⊇F(X)⊗F(Y),

则F称之为I(2U)上的模糊滤子,全体模糊滤子之集记为FF(I(2U))。

命题2[18]设I(2U)是一个区间集上非交换剩余格,F∈FI(2U),则F是I(2U)上的一个模糊滤子的充要条件为：

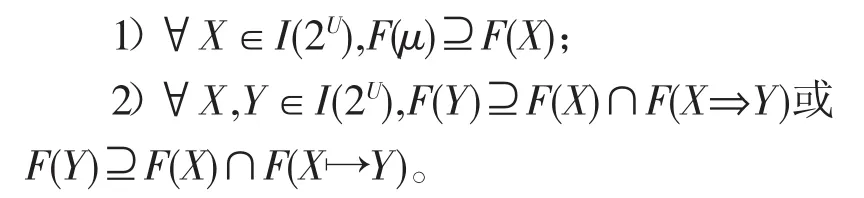
命题3设I(2U)是一个区间集上非交换剩余格,F∈F(I(2U))，则以下条件等价：

1）F是I(2U)上的一个模糊滤子；

2)∀X,Y,Z∈I(2U),如果 X⇒(Y⇒Z)=Ø,则F(Z)⊇F(X)∩F(Y)；

3)∀X,Y,Z∈I(2U),如果 X→(Y→Z)=μ,则F(Z)⊇F(X)∩F(Y)。

2 I(2U)广义模糊布尔滤子的特征性质

定义5设I(2U)是区间集上非交换剩余格,F∈F(I(2U)),若 F 满足∀X,Y∈I(2U)，XUXˉ∈I(2U)且 X∪X˜∈I(2U)，则称 F 为 I(2U)上的一个广义布尔滤子，这里 Xˉ=X⇒Ø,X˜=X→Ø。

定义6设I(2U)是区间集上非交换剩余格,F∈FF(I(2U)),若有关系式：

∀X∈I(2U),F(X∪Xˉ)=F(X∪X˜)=F(μ),则 F 称为I(2U)上的一个广义模糊布尔滤子。

定理1设I(2U)是区间集上非交换剩余格,F,G∈FF(I(2U)),F⊆G 且 F(μ)=G(μ)，若 F 是 I(2U)上的一个广义模糊布尔滤子，则G也是I(2U)上的一个广义模糊布尔滤子。

证明设∀X,Y∈I(2U)，由F是I(2U)上的一个广义模糊布尔滤子及题设条件可得

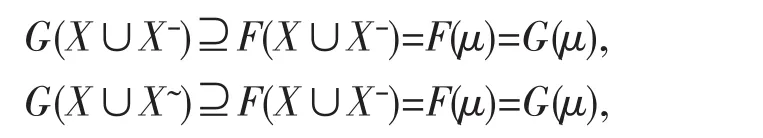
从而 G(X∪Xˉ)=G(X∪X˜)=G(μ),故 G 也是I(2U)上的一个广义模糊布尔滤子。

定理2设I(2U)是区间集上非交换剩余格,F∈FF(I(2U)),则以下条件等价：

1）F是广义模糊布尔滤子；

证明由 1）推出定理 2中 2）。设 X,Y∈I(2U)，则由性质1之7）知：

可类似地证得F(X→Y)⊇F(X→(Y˜⇒Y))。

由定理2中2）推出定理2中3)。设X，Y∈I(2U)，因为 φ⊆Y，则由性质 1 之 1）知 Xˉ=X⇒φ⊆X⇒Y，进而有(X⇒Y)→X⊆Xˉ→X，故

可类似证得 F(X)⊇F((X→Y)⇒X)。

故证得定理2中3）成立。

由定理2中3）推出定理2中4）。不妨在定理 2 中 3）中令 Y=Ø,可证式 4）成立。

由定理2中4）推出定理2中1）。设X∈I(2U)，由于(X∪Xˉ)ˉ=Xˉ∩(Xˉ)ˉ⊆X∪Xˉ，则依据性质 1.1之 2）得到(X∪Xˉ)ˉ→(X∪Xˉ)=μ，继而

F((X∪Xˉ)ˉ→(X∪Xˉ))=F(μ),又结合定理 2 中4）有

F((X∪Xˉ)ˉ→(X∪Xˉ))⊆F(X∪Xˉ)，故 F(X∪Xˉ)=F(μ)。可类似证得 F(X∪X˜)=F(μ)。这样证得 F是广义模糊布尔滤子。

定理3设I(2U)是区间集上非交换剩余格,F是I(2U)上的一个模糊广义布尔滤子，∀X,Y∈I(2U)，则以下性质成立：

证明1)设∀X,Y∈I(2U),则由性质1之5)知

(X∪Xˉ)⇒(X⇒Y)=(X⇒(X⇒Y))∩(Xˉ⇒(X⇒Y)=X⇒(X⇒Y),则 F((X∪Xˉ)⇒(X⇒Y))=F(X⇒(X⇒Y))。又因为F是广义模糊布尔滤子,所以F(X⇒Y)⊇F(X∪Xˉ)∩F((X∪Xˉ)⇒(X⇒Y)=F(μ)∩F(X⇒(X⇒Y))=F(X⇒(X⇒Y))。

可以类似证明F(X→Y)⊇F(X→(X→Y)。

2）设∀X,Y∈I(2U),一方面，依据性质 1之 7）有 X⊆(Y→X)⇒X，从而((Y→X)⇒X)˜⊆X˜⊆X→Y，进一步得到(X→Y)⇒Y⊆((Y→X)⇒X)˜⇒Y⊆((Y→X)⇒X)˜⇒ ((Y→X)⇒X)。

又因为F是广义模糊布尔滤子，则

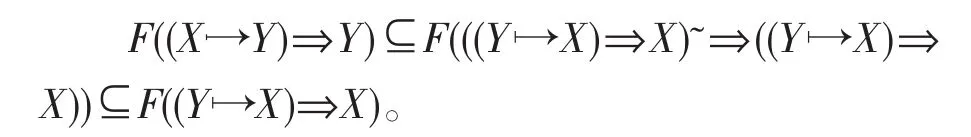
另一方面，根据性质1之7）有Y⊆(X→Y)⇒Y，

从而((X→Y)⇒Y)˜⊆Y˜⊆Y→X,

进一步得到

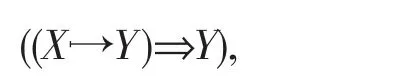
又因为F是广义模糊布尔滤子，所以

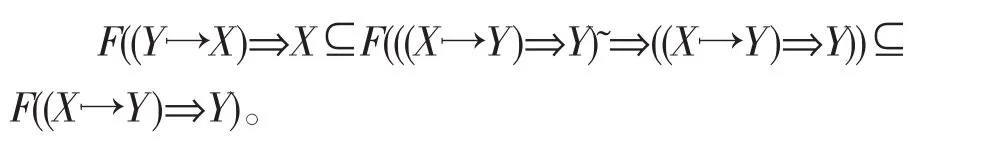
故由以上两方面得到F((X→Y)⇒Y)=F(Y→X)⇒X))。

可以类似证明第二式也成立。

3)设∀X，Y∈I(2U),依据性质 1 之式 5）及 2）可知：

因为F是广义模糊布尔滤子，所以

F(X)⊇F(X∪X˜)∩F((X∪X˜)→X˜)⊇F(μ)∩F(X˜→X)=F(X˜→X)。又由于 X˜⊆X→Y，则根据性质之 1之 1）有(X→Y)→X⊆X˜→X，因而由定义4 得到 F((X→Y)→X)⊆F(X˜→X),进一步有 F(X)⊇F((X→Y)→X)，再依据性质 1 之 6）知 μ⇒(Y→X)⊆((Y→X)⇒X)→(μ⇒X)，由性质 1 之 2）有 Y→X⊆((Y→X)⇒X)→X，再由性质 1 之 1）得到(Y→X)→(((Y→X)⇒X)→Y)⊇(((Y→X)⇒X)→X→(((Y→X)⇒X)→Y)⊇X→Y,

又因为Y⊆((Y→X)⇒X)→Y，则由性质1之1）有 Y→X⊇(((Y→X)⇒X)→Y)→X，从而再根据性质1之1）得

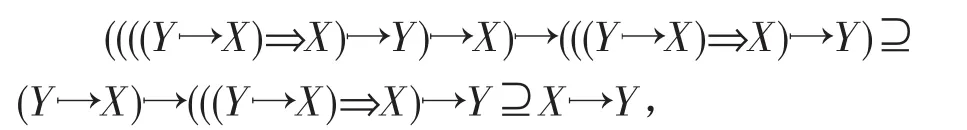
从而

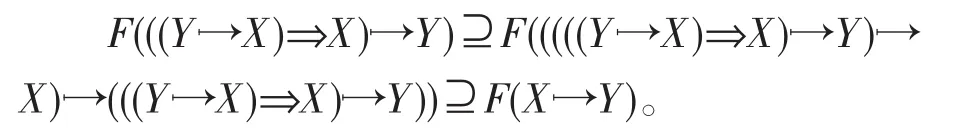
同样类似的方法可以证得F(((Y⇒X)→X)⇒Y)⊇F(X⇒Y)。

3 结语

本文是区间集思想和滤子理论应用于非交换剩余格上，引入了区间集上非交换剩余格广义模糊布尔滤子的定义，研究了其等价性刻画和基本特征性质表示定理。是否可以建立区间集非交换剩余格的相应广义模糊代数结构，将成为进一步深入探讨的问题。

参考文献：

[1]LOTFLA ZADEH.Fuzzy sets[J].Information and Control,1965，8(3)：338-353.

[2]ROSENFELD A. Fuzzy groups [J]. Journl of Mathematical Analysis and Applications,1971,35：512-517.

[3]PU B M,LIU Y M.Fuzzy topologyⅠ：Neighborhood structure of a fuzzy point and Moore-Smith convergence[J].Journal of Mathematical Analysis and Applications,1980,76(2)：571-599.

[4]PU B M,LIU Y M.Fuzzy topologyⅡ：Product and quotient spaces[J].Journal of Mathematical Analysis and Applications,1980,77(2)：20-37.

[5]BHAKAT S K,DAS P.On the defmition of a fuzzy subgroup[J].Fuzzy Sets Systems,1992,51：235-241.

[6]BHAKAT S K,DAS P.fuzzy subgroup[J].Fuzzy Sets Systems,1996,80：359-368.

[7]BHAKAT S K,DAS P.Fuzzy subrings and ideals redefined[J].Fuzzy Sets Systems,1996,81：383-393.

[8]ZHANG C．(∈',∈'∨q')-fuzzy subgroups[J].Fuzzy Sets Systems,1990,35(1)：121-124.

[10]YUAN X H.Generalized fuzzy Subgroups and many-Valued Implications [J].Fuzzy Sets and Systems,2003,138：205-211.

[11]LIAO Z H. (ϵ,ϵq(λ,μ))-fuzzy normal subgroup[J].Fuzzy Systems and Mathematics,2006,20(5)：47-53.

[12]YAO Y Y.Interval sets and Interval-set Algebras[C].The 8th IEEE International Conference on Cognitive informatics.Hong Kong：IEEE Computer Society,2009：307-314.

[13]姚一豫.区间集[M]//王国胤,李德毅,姚一豫,等.云模型与粒计算.北京：科学出版社,2012：74-93.

[14]YAO Y Y.Two views of theory of rough sets in finite universes [J].International Journal of Approximation Rersoning,1996,15(4)：291-317.

[15]WANG Z D,FANG J X.On ν-filters and normal ν-filters of a residuated lattice with a weak νt-operator[J].Information Sciences,2008,178：3465-3473.

[16]王国俊.非经典数理逻辑与近似推理(第二版)[M].北京：科学出版社,2008：155-206.

[17]裴道武.基于三角模的模糊逻辑理论及其应用[M].北京：科学出版社,2013：42-47.

[18]佩捷.从布尔到豪斯道夫：布尔方程与格论漫谈[M].哈尔滨：哈尔滨工业大学出版社,2014：282-292.

[21]罗俊丽，乔希民，吴洪博.区间集上非交换剩余格fuzzy滤子的特征性质[J].西南师范大学学报(自然科学版),2016,41(4)：20-24.