我国住房反向抵押贷款的长寿风险分析——基于Black-Scholes期权定价方法

张英琪胡伟西南财经大学保险学院

我国住房反向抵押贷款的长寿风险分析
——基于Black-Scholes期权定价方法

张英琪胡伟西南财经大学保险学院

一、背景介绍

自新中国成立以来，第一个五年经济计划后，中国人口死亡率由1949年的20‰下降到1957年的10.8‰。在改革开放后，我国人口死亡率从1970年的7.6‰下降到2013年的5.86‰。中国人的平均预期寿命由1981年的67.77岁上升至2010年的74.83岁，且平均预期寿命延长的趋势仍在继续。

上个世纪80年代中期后，老年人口比重每年持续增加。根据世界卫生组织（WHO）的定义：“一个国家65岁以上的人口占总人口的7%以上（或60岁以上的人口占总人口的10%以上）即称为老龄化社会，14%以上则称老龄社会，20%以上则称超老龄社会。”中国在2000年时，65岁以上的人口占比就已经达到了7%，截至2014年，我国60周岁及以上人口有21242万人，占总人口的15.5%，65岁以上的人口占总人口的10.1%，人口老龄化不断加剧。根据全国老龄办的预测，到2020年，我国老年人口将达到2.48亿，老龄化水平将达到17%。

综上所述，在人口老龄化社会背景下，中国的长寿风险与日俱增。对个人而言，长寿风险是个人在其寿命期限内的累计支出超过自身累积财富导致退休金短缺的风险。对政府而言，我国政府是养老保险的主要提供者，长寿风险会增加养老基金的支出，加重政府的财政负担。

在中国，老年人的收入主要来自儿女的供给、社会养老保险、工作时积累的企业年金或者职业年金。由于上个年代的生育政策，我国现在大部分家庭结构是“421”型和“8421”型，随着二胎政策的开放，家庭结构将走向“422”结构，这使得传统的家庭养老模式受到冲击。企业年金和职业年金在我国普及范围并不广泛，2015年领取企业年金的仅有89.7万人。对于大部分退休老人，收入的主要来源是社会养老保险，可是我国的社会养老保险从现收现付制转向积累制，个人账户并未落实，社保基金也面临巨额缺口。

▶图11953—2013年人口年龄结构和抚养比

因此，在现在的时代背景下，探索新的养老方式，充分利用老年人生命周期内的资源，借助于现有的金融和非金融体系，保证老年人的收入，保障老年人的老年生活幸福安康是十分必要的。

2013年，中国部分城市开展了“以房养老”养老产品的试点，该产品借鉴了美国的“以房养老”模式，而美国的“以房养老”模式的本质是住房反向抵押贷款。住房反向抵押贷款主要会面临利率风险、长寿风险、房价波动风险和道德风险。本文主要探究在老龄化背景下的中国，“以房养老”的养老模式是否会面临长寿风险。

二、选择的死亡率情景

截至目前，我国有三张人寿保险生命表，但由于第三张人寿生命表于2017年1月1日正式启用，故本文选取前两张生命表即CL（1990-1993）和CL（2000-2003）运用期间的数据进行分析。通过对比2000年、2010年和2013年全国分年龄死亡率，我们发现十几年来各年龄阶段的死亡率明显降低，特别是高年龄阶段的死亡率下降得更为明显。对年金类保险来说，沿用CL（2000-2003）会严重低估长寿风险。

为了精确地衡量住房抵押反向贷款中的长寿风险，我们纳入日本死亡率作为参考。众所周知，中国在拥有自己的第一张生命表之前，用的都是日本生命表，因为就人体内在因素而言，中国人和日本人的基因构成相似。基于HMD数据库，我们用SPSS软件，对中国2000年和2010年全国死亡率的数据与日本1947至2012年全国死亡率数据进行相关性分析，发现两国人口死亡率相关性很强（我国2000年的死亡率与日本1978年和1980年相关性最高，而2013年死亡率与日本1991年的死亡率相关性最高）。因此，我们选取日本的人口死亡率作为预测未来我国人口死亡率变化的参考。

随后我们进一步分析两国高龄人口死亡率的变化。

我们观察图4发现，随着日本国内经济的发展，日本65岁以上的人死亡率经历了一个快速下降到逐步稳定的过程。

图5显示，最近20年来，中国老龄人口的死亡率呈下降趋势。而中国是一个发展中国家，我们的医疗水平和相关健康意识都还有提高的余地，死亡率有可能会进一步下降，也有可能逐步趋于稳定。

在此假设三个死亡率的情景：情景一是好的情景，即未来死亡率和2000年的年金表中的死亡率一直保持一致；情景二是中等的情景，即中国现在死亡率还处于下降状态，未来高龄人群死亡率会和日本2010年时稳定的死亡率保持一致；情景三是最差的情景，相对于CL（2000-2003），未来我国高龄人群死亡率会下降一半。

三、房屋反向抵押贷款的期权定价模型

为了方便研究和考虑到家庭财富代际间传递的中国本土文化，我们将研究对象确定为有赎回权的住房反向抵押贷款养老产品。

根据有赎回权的住房反向抵押贷款的定义，我们将其视为一种欧式看跌期权，如果在抵押贷款合同到期时，房屋价值超过贷款人给付给借款人的贷款本息之和，借款人可以选择偿还其所有贷款赎回自有房屋；反之，如果房屋价格低于贷款人给付的贷款本息之和,借款人会放弃执行赎回自有房屋的权利。

我们假设贷款人支付给借款人贷款的本息之和XeRt=K（R为贷款合同的利率水平），K为期权的执行价格。当合同结束时，如果房屋价格小于贷款人支付给借款人的贷款额度st＜K，借款人在合同到期后不执行该期权；如果房屋价格大于贷款人支付给借款人的贷款额度st＞K，借款人在合同到期后有动机选择执行期权。所以，合同结束时，贷款人收入的现值等于房价期望的现值减去期权价格，即

根据等价原则，贷款人在合同生效时一次性支付给借款人的贷款总额等于贷款人在合同结束时从借款人处得到的收益的现值。为了计算贷款额，我们需要计算抵押房屋未来价格和赎回权的价值。

在金融市场中，一般都假设基础资产的价格变动服从几何布朗运动。因此我们假设房价的变化跟股价的变化相同，都服从几何布朗运动

其中：st表示合同已经生效t时间长度的房屋价格，

μ表示房屋价格的预期收益率，

σ表示房屋价格的波动率，

wt表示标准布朗运动。

根据前面的分析，我们可以得到贷款人在合同结束时的收益的现值用公式表现为

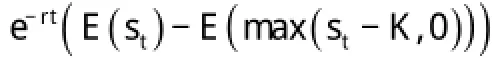
由房屋价格服从几何布朗运动：

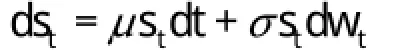
可求得：

到期具有赎回权的反向抵押贷款合同中期权价格为

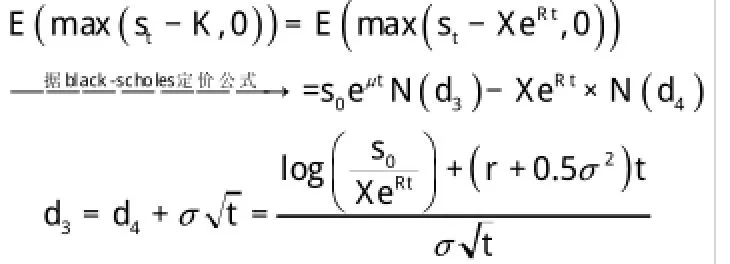
综合上述结果，我们可以得到合同到期贷款人能够获得的收益现值（也即借款人在合同生效时最多能够获得的一次贷款额度满足以下公式：

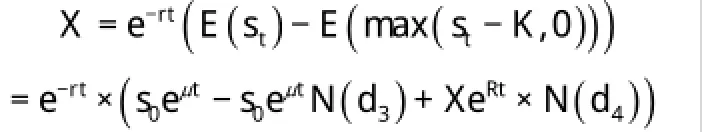
其中：X是合同存续时间t的函数，X=X(t)。

X(t)表示拥有赎回权的借款人在参保t年后死亡，借款人能够在合同生效时获得的贷款额度，对于单个借款人的余命是不确定的，是一个随机变量。

假设x岁的借款人的余命为t∈(0,w-x)，借款人合同生效时能够借到的贷款X(t)，借款人的余命密度函数为fx(t)，则借款人能借到的贷款期望为L=X(t)×(t)dt。三部分的模型，求解两种死亡率情景下的住房抵押贷款的一次性支付额。根据两种情景下的定价结果，得到系统性长寿风险对住房抵押贷款经营的影响。

为了得到某种死亡率情景下，合同生效时借款人能够获得的贷款数额，首先对房屋价格服从的几何布朗运动过程的参数进行估计，然后根据第三章模型得到不同余命的借款人合同生效时能够获得的一次性贷款数额，最后代入相应的死亡率数据，得到借款人在合同生效时获得一次性贷款的期望值。

以下实证分析采用成都市商品房2011年7月到2015年12月销售价格作为房价数据。

四、实证分析

（一）房屋价格函数的参数估计

根据模型关于房价的假设，房价服从几何布朗运动：

为了度量系统性长寿风险对保险机构经营住房反向抵押贷款的影响，我们根据第

2011年7月2011年8月2011年9月2011年10月2011年11月2011年12月2012年1月2012年2月2012年3月2012年4月2012年5月2012年6月2012年7月2012年8月2012年9月2012年10月2012年11月2012年12月2013年1月2013年2月2013年3月2013年4月2013年5月2013年6月2013年7月2013年8月2013年9月6984 6646 6612 6800 7011 6449 6582 6482 6311 6708 6538 6626 6260 5945 7057 7465 6945 6707 6962 6960 6939 7260 7212 7374 7489 7607 7413 2013年10月2013年11月2013年12月2014年1月2014年2月2014年3月2014年4月2014年5月2014年6月2014年7月2014年8月2014年9月2014年10月2014年11月2014年12月2015年1月2015年2月2015年3月2015年4月2015年5月2015年6月2015年7月2015年8月2015年9月2015年10月2015年11月2015年12月7506 8135 7481 8047 7737 7510 7745 7272 7455 8208 7687 7951 7703 7406 7846 6889 7352 7294 6983 7324 7794 7830 7690 7749 7744 7523 7857

通过表1中成都市商品房2011年7月到2015年12月的销售价格，根据Yt性质，可估计出房屋价格的预期收益率μ、房屋价格的波动率σ。

（二）住房反向抵押贷款一次性支付额

根据生命表的死亡数据，求解住房反向抵押贷款一次性支付额，假设借款人在合同生效的第k+1年内死亡，且反向抵押房屋在年末变现，根据第三部分的模型变换，其在合同生效时刻能够获得的一次性贷款可以得到：

如果我们计算一次性贷款额时不考虑具有赎回权的期权价格，仅仅考虑合同到期时房屋期望价格的折现值，虽然与合理定价有差距，但是这可以视为

基于死亡率数据，住房反向抵押贷款合同的一次性贷款给付L（x）是合同生效后x岁的借款人在以后各年死亡时能获得的一次性贷款现值在死亡概率下的平均值。

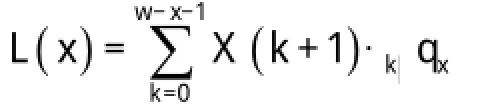
假设成都市的一位老人从2016年参加住房反向抵押贷款，则2016年初成都商品房价为s0，根据收集到的成都商品房价格数据，则s0=7857，同时设合同的无风险利率r=0.02,合同利率R=0.035。首先根据上述分析求出，代入相应的死亡率数据可得到相应的房屋反向抵押贷款的定价。本文根据CL（2000-2003）（男）、日本2010年全国死亡率数据（男）和假设的第三个情景下的生命表，分别计算出相应死亡率下，60岁到65岁的老年人在住房反向抵押贷款合同生效时一次性可以获得的贷款额。为了分析方便，我们此处仅考虑每平方米的住房反向抵押贷款合同在合同生效时刻能够获得的一次性贷款额。

由表2可知，在同一张死亡率表下，借款人参保时年龄越大，能够获得的一次性贷款越小。这是因为根据生命表中的死亡率数据，年龄越大，其预期余命越短，从而合同的期限越短，合同期限越短，房屋未来的预期增值越小，导致借款人年龄越大，其获得的一次性贷款反而越小。

对比在CL（2000-2003）下和在日本2010年全国不同年龄死亡率表，我们发现借款人能领取的每平方米一次性住房抵押贷款的差别不大，即使与最差的情景三（死亡率下降了50%）对比，每平方米一次性住房抵押贷款额度都相差不大。这意味着在现有的房屋价格增长情况下，如果中国未来的死亡率和日本一样，排除医疗水平有很大的突破的情况，最终高龄人群死亡率收敛于同一值，长寿风险将不是住房反向抵押贷款的主要风险，并且长寿风险在房地产市场中能被很好地分散掉。

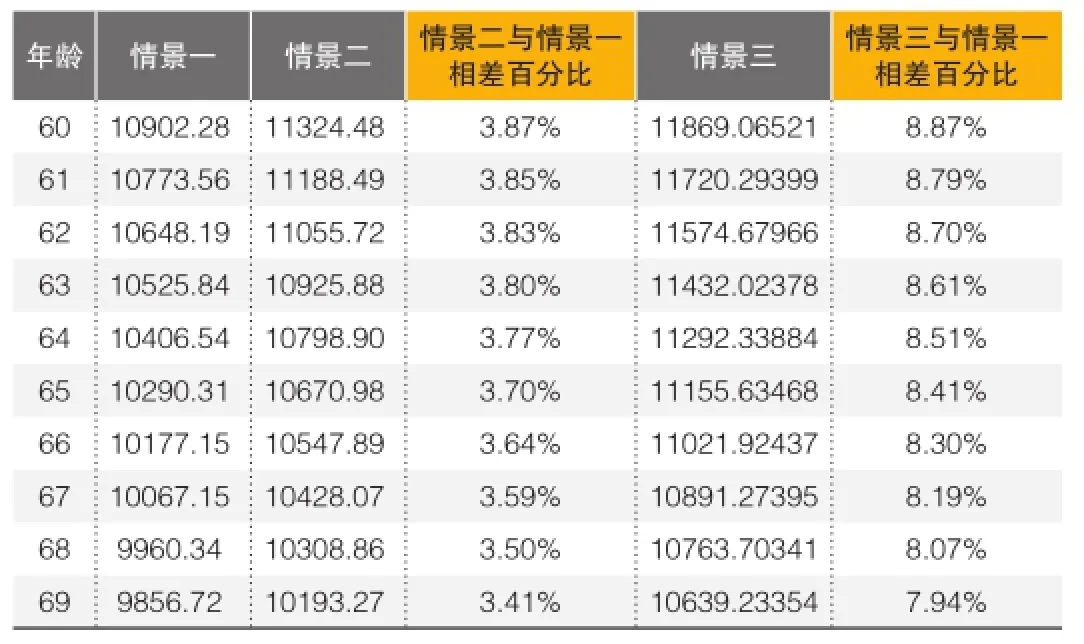
年龄60 61 62 63 64 65 66 67 68 69情景一10902.28 10773.56 10648.19 10525.84 10406.54 10290.31 10177.15 10067.15 9960.34 9856.72情景二11324.48 11188.49 11055.72 10925.88 10798.90 10670.98 10547.89 10428.07 10308.86 10193.27情景二与情景一相差百分比3.87% 3.85% 3.83% 3.80% 3.77% 3.70% 3.64% 3.59% 3.50% 3.41%情景三11869.06521 11720.29399 11574.67966 11432.02378 11292.33884 11155.63468 11021.92437 10891.27395 10763.70341 10639.23354情景三与情景一相差百分比8.87% 8.79% 8.70% 8.61% 8.51% 8.41% 8.30% 8.19% 8.07% 7.94%

（三）住房反向抵押定价拓展--房价增长率对长寿风险的影响

为了更进一步分析房屋价格波动对住房反向抵押贷款面临的系统性的长寿风险的影响，我们假设住房价格波动率σ不变，μ值分别取不同的值，计算在CL（1990-1993）和CL（2000-2003）下的每平方米住房反向抵押贷款合同的一次性贷款额。在此我们引入自定义的盈利百分比概念：

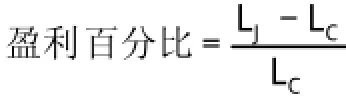
其中：LJ为按照日本2010年死亡率计算得到的一次性贷款额，LC为按照CL（2000-2003）计算得到的一次性贷款额。

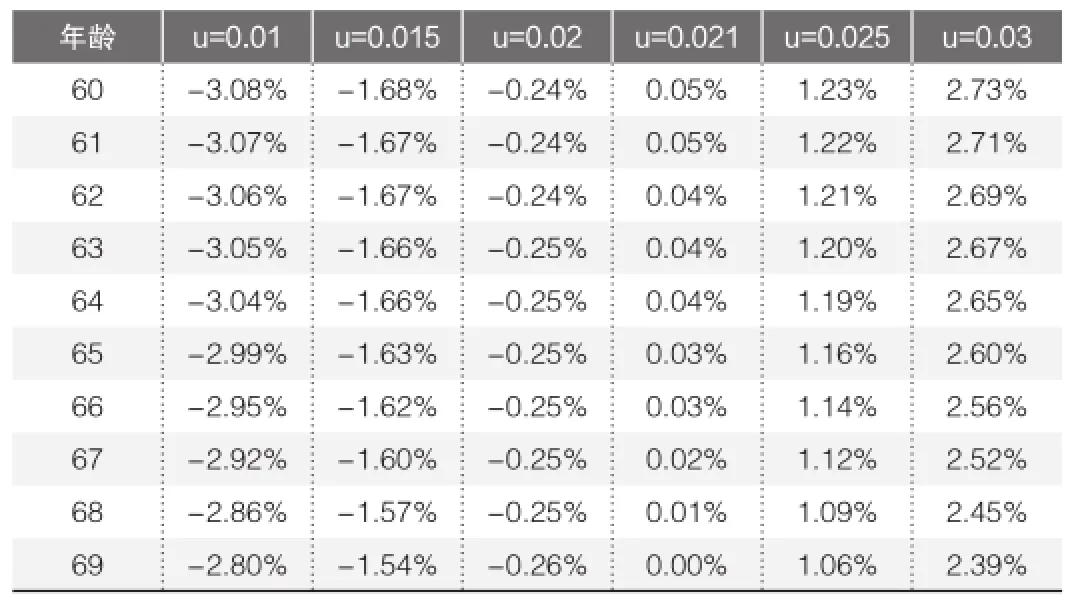
年龄6 0 6 1 6 2 6 3 6 4 6 5 6 6 6 7 6 8 6 9 u = 0 . 0 1 -3 . 0 8 % -3 . 0 7 % -3 . 0 6 % -3 . 0 5 % -3 . 0 4 % -2 . 9 9 % -2 . 9 5 % -2 . 9 2 % -2 . 8 6 % -2 . 8 0 % u = 0 . 0 1 5 -1 . 6 8 % -1 . 6 7 % -1 . 6 7 % -1 . 6 6 % -1 . 6 6 % -1 . 6 3 % -1 . 6 2 % -1 . 6 0 % -1 . 5 7 % -1 . 5 4 % u = 0 . 0 2 -0 . 2 4 % -0 . 2 4 % -0 . 2 4 % -0 . 2 5 % -0 . 2 5 % -0 . 2 5 % -0 . 2 5 % -0 . 2 5 % -0 . 2 5 % -0 . 2 6 % u = 0 . 0 2 1 0 . 0 5 % 0 . 0 5 % 0 . 0 4 % 0 . 0 4 % 0 . 0 4 % 0 . 0 3 % 0 . 0 3 % 0 . 0 2 % 0 . 0 1 % 0 . 0 0 % u = 0 . 0 2 5 1 . 2 3 % 1 . 2 2 % 1 . 2 1 % 1 . 2 0 % 1 . 1 9 % 1 . 1 6 % 1 . 1 4 % 1 . 1 2 % 1 . 0 9 % 1 . 0 6 % u = 0 . 0 3 2 . 7 3 % 2 . 7 1 % 2 . 6 9 % 2 . 6 7 % 2 . 6 5 % 2 . 6 0 % 2 . 5 6 % 2 . 5 2 % 2 . 4 5 % 2 . 3 9 %

从表3可以看出，如果我国的人口死亡率朝着日本2010年人口死亡率方向收敛，随着房价预期增长率越大，住房反向抵押贷款面临的长寿风险越小，甚至给住房反向抵押贷款提供方带来长寿机遇。当房价预期增长率为0.021时，长寿风险带来的影响几乎可以忽略；当房价预期增长率大于0.021时，其面临的长寿风险会给住房反向质押贷款提供方带来正收益；当房价预期增长率小于0.021时，住房反向质押贷款提供方面临的长寿风险会给其带来损失。

由此可得，住房反向质押贷款提供方面临的风险具有交叉作用效应。

五、结论与建议

如果未来房屋价格保持成都市2011年至2015年的增长速度、我国人口死亡率最终收敛于日本稳定人口死亡率的状态，那么长寿风险将不是住房反向抵押贷款面临的主要风险，“以房养老”新型养老方式将会是有效地分散我国老龄化背景下长寿风险的手段。

过去的十几年间，我国的经济处于繁荣期，房地产市场欣欣向荣，房价波动式地向上增长。根据国内研究表明，我国房价周期与经济周期同步，在经济繁荣期，房价会在大背景下有好的增长预期，可是如果经济周期进入衰退或萧条期，房价预期的增长则不可能实现。通过计算可以发现，在不考虑利率风险的情况下，只要房屋价格预期增长率在2.1%以上，住房反向贷款面临的长寿风险可以被分散；可是如果房价低于2.1%的增长速度，房价波动的风险会扩大长寿风险的影响。因此住房反向抵押贷款的提供方需要清楚地认识提供产品时的经济周期的变化和房价未来预期的变化带来的影响，当房价预期增长率低于2.1%时，住房反向抵押贷款的提供方需要重新审核自己的风险管理，并进行新的资产配置，或者调整住房反向抵押贷款的定价水平。另外，本文假设中国未来人口死亡率收敛到日本目前稳定的死亡率水平，但是如果未来中国的死亡率因为医疗水平的重大突破，发生更大的变化甚至进一步降低，低于日本目前的死亡率，那么长寿风险对住房反向抵押贷款提供方的影响需要根据房价预期增长率的大小具体测算。

本文通过将连续的模型离散化，引入与中国死亡率关联程度高的日本死亡率作为中国未来死亡率的参考，根据两张生命表得出的定价，比较分析长寿风险对住房反向抵押贷款提供方的影响；且突出考虑了房价预期增长率变动时，长寿风险对住房反向抵押贷款提供方影响的变化，得出结论：长寿风险的破坏力因房地产市场的行情不同而不同。不足之处是：第一，没有考虑利率风险；第二，没有考虑房屋土地使用权到期后需缴纳的土地出让金和房屋的折旧。SIM