Monomial Derivations without Darboux Polynomials
2017-05-11LIJIANTAO
LI JIAN-TAO
(School of Mathematics,Liaoning University,Shenyang,110036)
Monomial Derivations without Darboux Polynomials
LI JIAN-TAO
(School of Mathematics,Liaoning University,Shenyang,110036)
Communicated by Du Xian-kun
In this paper,it is proved that a monomial derivationdofk[x,y,z]has no Darboux polynomials if and only ifdis a strict derivation with a trivial ring of constants,and we give the specif i c conditions when it has no Darboux polynomials.
derivation,monomial derivation,Darboux polynomial,ring of constants
1 Introduction
Throughout this paper,letk[X]=k[x1,x2,···,xn]denote the polynomial ring over a f i eldkof characteristic 0.
Derivations and Darboux polynomials are useful algebraic methods to study the polynomial or the rational dif f erential systems.If we associate a polynomial dif f erential system
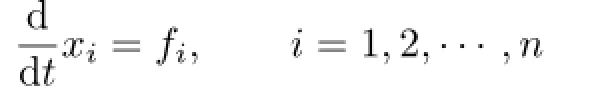
with a derivation
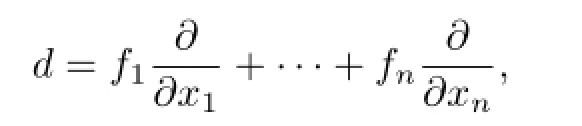
then the existence of the Darboux polynomials is a necessary condition for the system to have a f i rst integral(see[1]–[3]).It is of interest to know whether Darboux polynomials existfor any derivation ofk[X].However,in general,this problem is very diffi cult.Ink[x1,x2],dis a derivation without Darboux polynomials if and only ifdis a simple derivation,and only some sporadic examples of derivations without Darboux polynomials are known(see [4]–[6]).Forn≥3,the most famous example of derivations without Darboux polynomials is the Jouanolou derivation def i ned byd(x)=ys,d(y)=zsandd(z)=xs,s≥2(see[7]–[9]).
If a derivationdhas no Darboux polynomials,then the ring of constants ofd,denoted byk[X]d,must be trivial,that is,k[X]d=k.In 2006,Nowicki and Zieli´nski[10]gave a full description of all monomial derivations of the rational function f i eldk(X)with trivial fi eld of constants in two or three variables.They also proved that a generalized Jouanolou derivation

has a trivial f i eld of constants if and only ifpqr≥2.In 2008,Moulin Ollagnier and Nowicki[11]presented several new examples of homogeneous monomial derivations without Darboux polynomials ofk[x,y,z],in which case

andf1,f2andf3are homogeneous monomials of the same degrees≤4.In 2011,Moulin Ollagnier and Nowicki[12]proved that a strict monomial derivationdofk[x,y,z]has no Darboux polynomials if and only ifk(x,y,z)d=k.
In this paper,we show that a monomial derivationdofk[x,y,z]has no Darboux polynomials if and only ifdis strict and has a trivial ring of constants,that is,k[x,y,z]d=k. It should be noted that the conditionk[x,y,z]d=kcannot implyk(x,y,z)d=k.Even if a derivationdhas a trivial ring of constants ink[x,y,z],it may also exists a nonconstant rational functionfsuch thatd(f)=0.So the result in[12]mentioned above cannot imply our theorem.Moreover,we give the specif i c conditions when it has no Darboux polynomials, that is,dhas no Darboux polynomials if and only if

where the non-negative integersβijsatisfy neither of the following conditions:
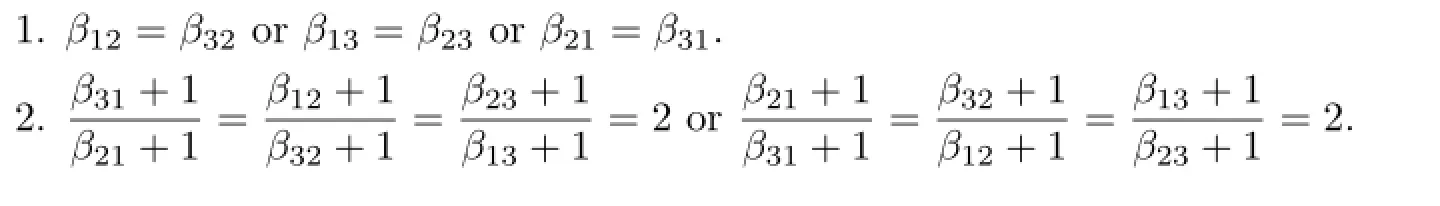
2 Notations and Preliminaries
In this section,we f i x notations and collect some basic facts;see[10]and[13]for details.
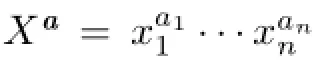
Lemma 2.1([13],Proposition 2.1.6)If d is a monomial derivation,then there exists a direction γ such that d is γ-homogeneous.
Lemma 2.2([13],Proposition 2.2.3)If d is a γ-homogeneous derivation of degree s and F is a Darboux polynomial of d with a cofactor Λ,then Λ is γ-homogeneous of degree s,and all γ-components of F are also Darboux polynomials with the common cofactor Λ.
Now we consider a monomial derivationddef i ned byd(xi)=Xβi,whereβi=(βi1,···,βin)∈Nn.Letβdenote then×nmatrix[βij]andαdenote the matrixβ−I,whereIis then×nidentity matrix.Letwd=detαand

wherek∗=k{0}.Foru=(u1,···,un)∈(k∗)n,letσudenote the diagonal automorphism def i ned byσu(xi)=uixi,i=1,···,n.Thenis equivalent tou∈G(α)from [10].
Lemma 2.3([10],Lemma 4.1])If wd0and u=(u1,···,un)∈G(α),then u1,···, unare the N-th roots of1,where N is the absolute value of wd.In particular,the group G(α)is f i nite.
A polynomialH∈k[X]is calledG(α)-invariant ifσu(H)=Hfor everyu∈G(α).It is clear that a nonzero polynomialHisG(α)-invariant if and only if each monomial ofHisG(α)-invariant.The following lemma is a restatement of Proposition 4.6 in[10]for the case of polynomials.
Lemma 2.4A monomial Xp∈k[X]is G(α)-invariant if and only if there exist r1,···, rn∈Zsuch that Xp=(Xα1)r1···(Xαn)rn,where αiis the i-th row of the matrix α.
3 Main Results
The aim of this section is to give a characterization of monomial derivations ofk[x,y,z] without Darboux polynomials.If a derivationdhas no Darboux polynomials,it is clear thatdis strict.Throughout this section,unless otherwise stated,letdbe a derivation def i ned by
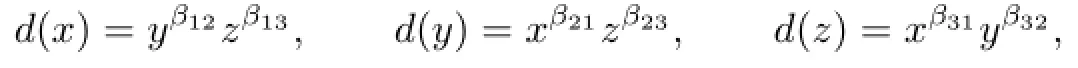
whereβij∈N.
Lemma 3.1The derivation d has a trivial ring of constants if and only if the non-negative integers βijsatisfy neither of the following conditions:
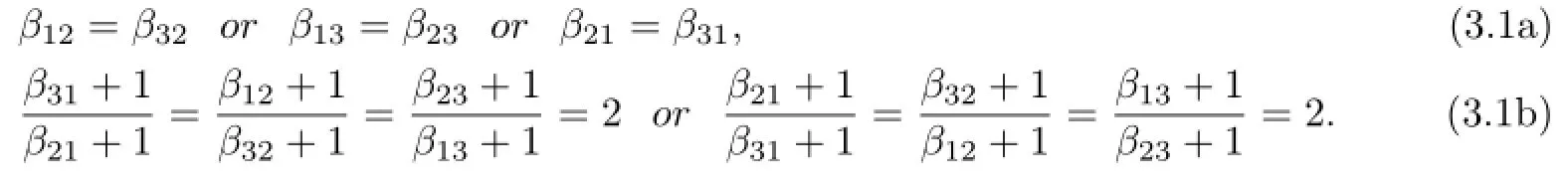

Suppose that the integersβijsatisfy the condition(3.1b).Without loss of generality,we may assume that
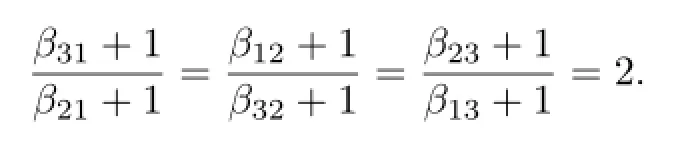
Let
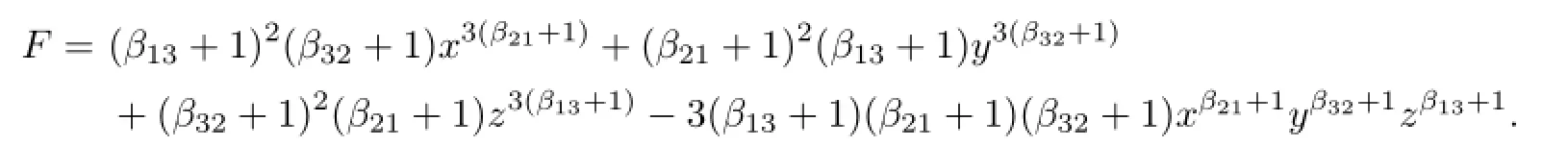
Thensinceβij+1>0.Moreover,d(F)=0,whencek[x,y,z]dk.
Conversely,suppose that the integersβijsatisfy neither the condition(3.1a)nor(3.1b). Putδ=xy z d.Thenk[x,y,z]d=k[x,y,z]δ.Since allβij≥0,we get
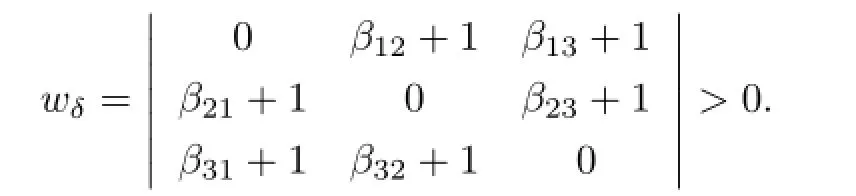
Noting thatβij∈N and applying Theorem 8.6 of[10],we havek[x,y,z]d=k.
Lemma 3.2Suppose that the derivation d has a trivial ring of constants.
(1)If wd0,then d is γ-homogeneous of degree s0with respect to some direction γ.
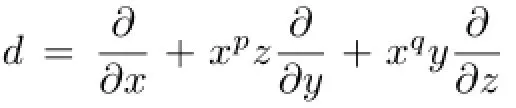
Proof.(1)By Lemma 2.1,there exists a directionγ=(γ1,γ2,γ3)such thatdisγhomogeneous of degrees,that is
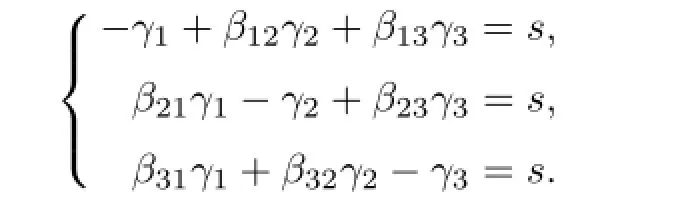
Since the determinant of coeffi cientswd0 and0,we have0.
(2)We f i rst claim that only one ofd(x),d(y),d(z)is contained ink.
Suppose that there exist at least two(say the f i rst two)ofd(x),d(y),d(z)are contained ink.Then

which satisf i es the condition(3.1a),implying thatk[x,y,z]dkby Lemma 3.1,a contradiction.
Suppose thatd(x),d(y),d(z).Thenβ12+β130,β21+β230 andβ31+β320. A routine calculation yields
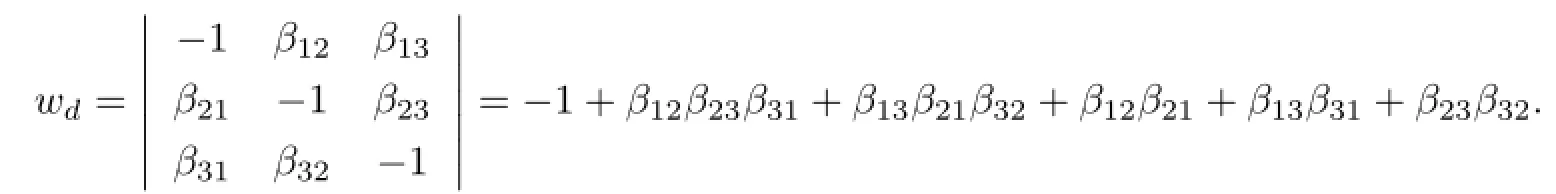
Sincewd=0,
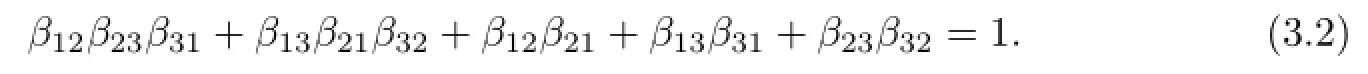
Thus every term on the left-hand side of the equation(3.2)is equal to 0 or 1 sinceβij∈N. Suppose thatβ23β32=1.Thenβ23=β32=1 andβ12β31+β13β21+β12β21+β13β31=0, whence(β12+β13)(β31+β21)=0.Sinceβ12+β130,we haveβ31+β21=0.Thusβ31=β21=0,which implies thatk[x,y,z]dkby Lemma 3.1,a contradiction.Henceβ23β32=0.Ifβ23=β32=0,then

Sinceβ31+β320 andβ21+β230,we haveβ310 andβ210.Moreover,β1323by Lemma 3.1,and henceβ130.It follows from(3.3)thatβ13=β31=1 andβ12=0=β32, contrary to Lemma 3.1.If only one ofβ23andβ32is 0,sayβ23=0 andβ320,thenβ130 by Lemma 3.1 andβ210 sinceβ21+β230.The equation(3.2)yields
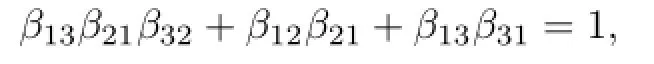
which implies thatβ13=β21=β32=1 andβ12=β31=0.Thus
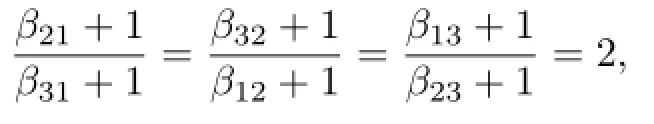
contrary to Lemma 3.1.
Now suppose that there is only one ofd(x),d(y),d(z)belongs tok.Taking a permutation of variables,we may assume thatd(x)∈kand
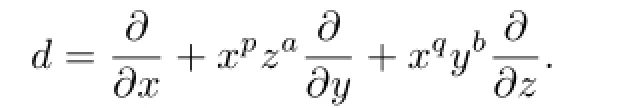
Lemma 3.1 implies that.Clearly,wd=ab−1.Sincewd=0,we getab=1,and soa=b=1.
Lemma 3.3Suppose that d has a Darboux polynomial F such that d(F)=ΛF.Then
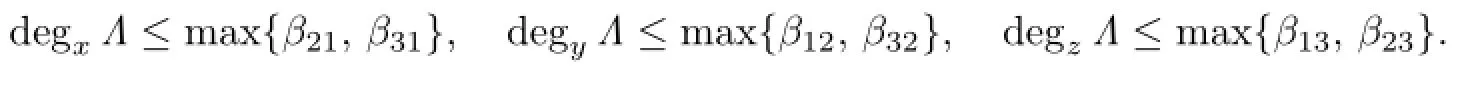
Proof.We only consider the case of degzΛ.Since
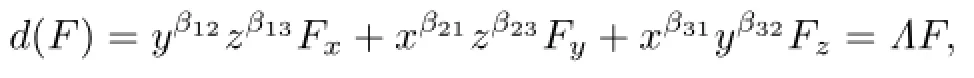
we have
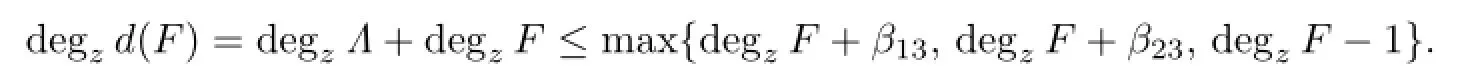
Thus
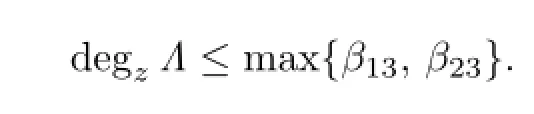
Theorem 3.1Let d be an arbitrary monomial derivation of k[x,y,z].Then the following statements are equivalent:
(1)d has no Darboux polynomials;
(2)d is a strict monomial derivation with a trivial ring of constants;
(a)β12=β32or β13=β23or β21=β31;
Proof.(2)⇔(3)is clear by Lemma 3.1 and(1)⇒(2)is trivial.
Now we deal with the case(2)⇒(1).It should be noted that the conditionk[x,y,z]d=kcannot implyk(x,y,z)d=k.The result in[12]is thatdhas no Darboux polynomials whenk(x,y,z)d=k.However,whenk[x,y,z]d=k,we cannot get the result thatk(x,y,z)d=k.So we cannot use the result in[12],that is,the result in[12]cannot imply our theorem.
Now suppose thatdis a strict monomial derivation with trivial ring of constants,that is,

andk[x,y,z]d=k.The proof is divided into two cases.
Case 1wd0.
By Lemma 3.2(1),there exists a directionγsuch thatdisγ-homogeneous of degree0. Suppose thatdhas a Darboux polynomialFsuch thatd(F)=ΛFfor someΛ∈k[x,y,z].
Choose an arbitraryu1∈G(α)and letσu1be the diagonal automorphism.Then,andis the identity map by Lemma 2.3,where.Let
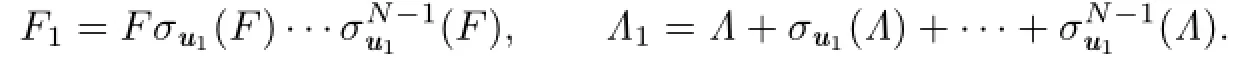
ThenF1is a Darboux polynomial with cofactorΛ1such thatσu1(F1)=F1andσu1(Λ1)=Λ1.Next,chooseu2∈G(α){u1}and the diagonal automorphismσu2.We can also get a Darboux polynomialF2with cofactorΛ2such thatσui(F2)=F2andσui(Λ2)=Λ2fori=1,2,where
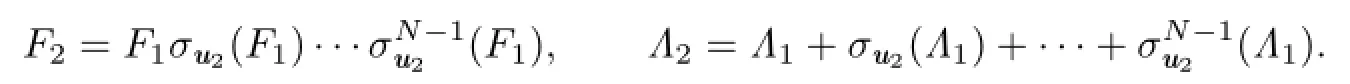
Proceed further in this direction.SinceG(α)is f i nite by Lemma 2.3,we can obtain a Darboux polynomialF′with cofactorΛ′such thatσu(F′)=F′andσu(Λ′)=Λ′for everyu∈G(α),that is,F′andΛ′areG(α)-invariant.Sincek[x,y,z]d=k,we haveΛ′0,andΛ′isγ-homogeneous of degreesby Lemma 2.2.
It is clear that a polynomial isG(α)-invariant if and only if its every monomial isG(α)-invariant.Then by Lemma 2.4,for every monomialxaybzcofΛ′,there existr1,r2,r3∈Z such that
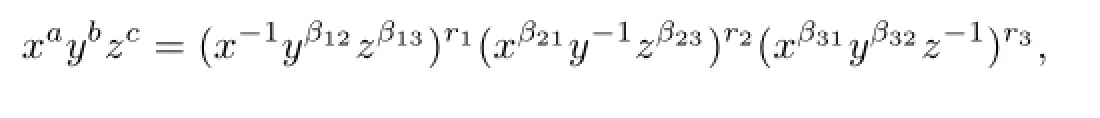
that is,
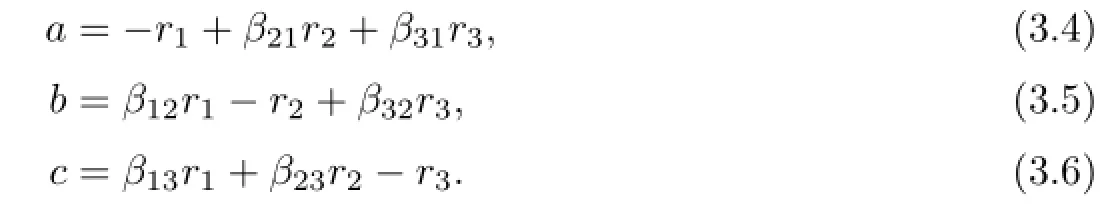
SincedandΛ′areγ-homogeneous of degrees,we have
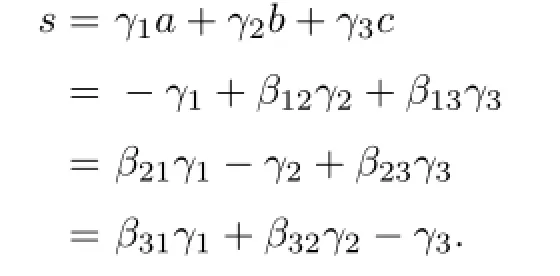
Thus
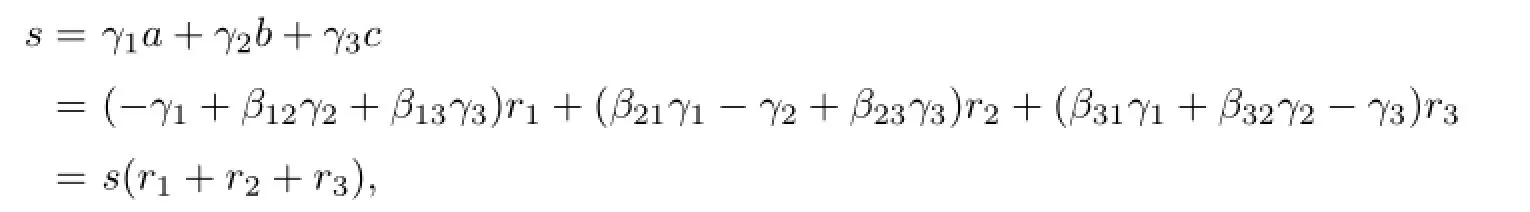
Since0,it follows thatr1+r2+r3=1.Without loss of generality,suppose thatr1≥r2≥r3.Ifr3≥0,thenr1=1,r2=r3=0.Thus the equation(3.4)implies thata=−r1=−1,which contradictsa≥0.Hencer3<0.Ifr2≤0,from the equation(3.4), we can also get

a contradiction.So we conclude thatr1≥r2≥1>0>−1≥r3.By Lemma 3.3,we havec≤degzΛ′≤max{β13,β23},butc=β13r1+β23r2−r3≥β13+β23+1>max{β13,β23},which is impossible.
Case 2wd=0.
Letσ:k[x,y,z]→k[x,y,z]be the automorphism def i ned by
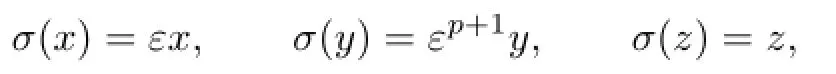
whereεis a primitiveroot of 1 and=p+q+2.It is easy to verify thatσ−idσi=εid. Let

Thenand.Sincen+1≤max{p,q}+1<p+q+2=andεis a primitive¯N-th root of 1,we get

Thus

So=0,contrary tok[x,y,z]d=k.Corollary 3.1If d is a derivation of k[x,y,z]def i ned by

where p,q,r∈N,then d has no Darboux polynomials if and only if pqr≥2.
Proof.For this derivation,β12=p,β23=q,β31=r,β13=β21=β32=0.Ifpqr=0 orpqr=1,then the integersβijsatisfy the condition(3.1a)or(3.1b).Thusk[x,y,z]dkby Lemma 3.1 and sodhas Darboux polynomials.Ifpqr≥2,without loss of generality, suppose thatp≥2.ThenThusβijdo not satisfy the conditions(3.1a) and(3.1b).Consequently,k[x,y,z]d=kanddhas no Darboux polynomials by Theorem 3.1.
Remark 3.1This is a generalization of the fact that the Jouanolou derivation
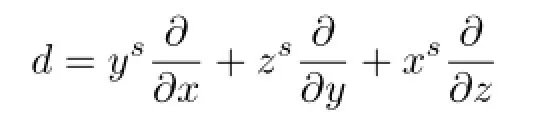
has no Darboux polynomials for alls≥2.
[1]Maciejewski A,Przybylska M.Darboux polynomials and fi rst integrals of natural polynomial Hamiltonian systems.Phys.Lett.A,2004,326:219–226.
[2]Maciejewski A,Moulin Ollagnier J,Nowicki A.Generic polynomial vector fi elds are not integrable.Indag.Math.,2004,15(1):55–72.
[3]Moulin Ollagnier J.Liouvillian fi rst integrals of homogeneous polynomial 3-dimensional vector if elds.Colloq.Math.,1996,70:195–216.
[4]Maciejewski A,Moulin Ollagnier J,Nowicki A.Simple quadratic derivations in two variables.Comm.Algebra,2001,29(11):5095–5113.
[5]Nowicki A.An example of a simple derivation in two variables.Colloq.Math.,2008,113(1): 25–31.
[6]Havran V S.Simple derivations of higher degree in two variables.Ukrainian Math.J.,2009, 61(4):682–686.
[7]Jouanolou J P.´Equations de Pfaf f alg´ebriques.Lect.Notes in Math.708,Berlin:Springer-Verlag,1979.
[8]Maciejewski A,Moulin Ollagnier J,Nowicki A,Strelcyn J M.Around Jouanolou nonintegrability theorem.Indag.Math.,2000,11:239–254.
[9]Zoladek H.Multi-dimensional Jouanolou system.J.Reine Angew.Math.,2003,556:47–78.
[10]Nowicki A,Zieli´nski J.Rational constants of monomial derivations.J.Algebra,2006,302: 387–418.
[11]Moulin Ollagnier J,Nowicki A.Derivations of polynomial algebras without Darboux polynomials.J.Pure Appl.Algebra,2008,212:1626–1631.
[12]Moulin Ollagnier J,Nowicki A.Monomial derivations.Comm.Algebra,2011,39(9):3138–3150.
[13]Nowicki A.Polynomial Derivations and Their Rings of Constants.Toru´n:N.Copernicus University Press,1994.
tion:13N15,12H05
A
1674-5647(2017)02-0185-08
10.13447/j.1674-5647.2017.02.10
Received date:Dec.30,2016.
Foundation item:The NSF(11526104)of China,and the Youth Research Funds(LDGY2015001)from Liaoning University.
E-mail address:jtlimath@qq.com(Li J T).
杂志排行
Communications in Mathematical Research的其它文章
- On Fundamental Group of a Certain Class of Welded Knots
- The Invariant Rings of the Generalized Transvection Groups in the Modular Case
- Two Bijections on Weighted Motzkin Paths
- Uniqueness in Determining a Ball with a Single Incoming Wave
- Growth of Solutions to Higher Order Dif f erential Equation with Meromorphic Coeffi cients
- A New Characterization on g-frames in Hilbert C∗-Modules
