Two Bijections on Weighted Motzkin Paths

CHEN ZHONG-JIN AND ZHAO SHUO

(School of Mathematics,Beijing Technology and Business University,Beijing,100048)

Two Bijections on Weighted Motzkin Paths

CHEN ZHONG-JIN AND ZHAO SHUO

(School of Mathematics,Beijing Technology and Business University,Beijing,100048)

Communicated by Du Xian-kun

In this paper,we provide a bijection between the set of underdiagonal lattice paths of lengthnand the set of(2,2)-Motzkin paths of lengthn.Besides,we generalize the bijection of Shapiro and Wang(Shapiro L W,Wang C J.A bijection between 3-Motzkin paths and Schr¨oder paths with no peak at odd height.J.Integer Seq.,2009,12:Article 09.3.2.)to a bijection betweenk-Motzkin paths and(k−2)-Schr¨oder paths with no horizontal step at even height.It is interesting that the second bijection is a generalization of the well-known bijection between Dyck paths and 2-Motzkin paths.

underdiagonal lattice path,(2,2)-Motzkin path,k-Motzkin path,(k−2)-Schr¨oder path

1 Introduction

For any positive integern,letPdenote an underdiagonal lattice path of lengthnin thexy-plane that:

(1)consists of right stepsR=(1,0),upward stepsW=(1,2)and vertical stepsV= (0,1);

(2)begins at(0,0)and terminates at(n,k),for 0≤k≤n;

(3)never rises above the liney=x.

The length of underdiagonal lattice pathP,denoted bylength(P),is equal ton,whose last step reaches linex=n.Fig.1.1 is an example of an underdiagonal lattice path of length 8.

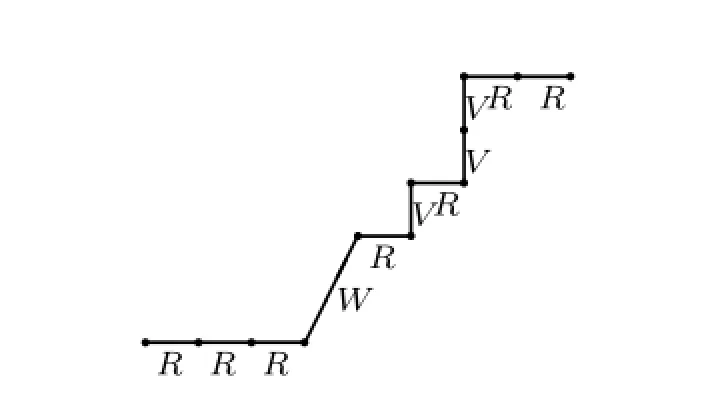
Fig.1.1 An underdiagonal lattice path of length 8

LetPndenote the set of underdiagonal lattice paths of lengthn,andpndenote the number ofPnwhich is listed as entry A071356 in OEIS(see[1]),and its f i rst few items are 1,2,6,20,72,272,1064,···See[2]for more information.

A Motzkin path of lengthnis def i ned as a lattice path from(0,0)to(n,0)consisting of up stepsU=(1,1),horizontal stepsH=(1,0)and down stepsD=(1,−1)that does not go below thex-axis.A(k,t)-Motzkin path is a Motzkin path that each horizontal step is colored with one of thekcolors 1,2,···,k,and each down step is colored with one of thetcolors 1, 2,···,t.Whilet=1,we call it ak-Motzkin path.A bijection between noncrossing linked partitions and large(3,2)-Motzkin paths was given by Chen and Wang[3].The properties of (3,2)-Motzkin paths have been extensively studied by Woan[4],[5].Recently,several papers on the combinatorics of Motzkin paths have been published(see[6]–[9]).

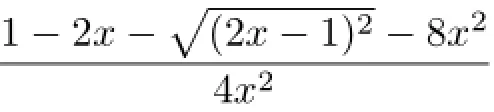
A Schr¨oder path of length 2nis a lattice path from(0,0)to(2n,0)that does not go below thex-axis and consists of up stepsu=(1,1),horizontal stepsh=(2,0)and down stepsd=(1,−1).Ak-Schr¨oder path is a Schr¨oder path whose horizontal steps could be colored by one ofkcolors.Yan[10]provided a one-to-one correspondence between(2,3)-Motzkin paths and Schr¨oder paths for the purpose of enumerating theUDDandLDsubsequences. A bijection between 3-Motzkin paths of lengthn−1 and Schr¨oder paths of length 2nwith no peak at odd height was given by Shapiro and Wang[11].In this paper,we generalize it to a bijection betweenk-Motzkin paths of lengthnand(k−2)-Schr¨oder paths of length 2n+2 with no horizontal step at even height.Restricting(k−2)-Schr¨oder paths to Dyck paths, we get the well-known bijection between 2-Motzkin paths and Dyck paths.One can see[12] to learn more about the bijection.

2 Underdiagonal Lattice Paths and(2,2)-Motzkin Paths

In this section,we aim to construct a bijection between the set of underdiagonal lattice paths of lengthnand the set of(2,2)-Motzkin paths of lengthn,and present some interestingproperties.

2.1 From Underdiagonal Lattice Paths to(2,2)-Motzkin Paths

Let~Pdenote an underdiagonal lattice path of lengthmthat begins at(0,0)and terminates at(m,m)form≥1,whose steps never rise the liney=xexcept at the origin and the destination.We call such path as an irreducible underdiagonal lattice path.Letφdenote the map from the set of underdiagonal lattice paths of lengthmto the set of(2,2)-Motzkin paths of lengthm.LetH1andH2denote horizontal steps of(2,2)-Motzkin path with color 1 and 2,and letD1andD2denote down steps with color 1 and 2,respectively.

Whilem=1 andm=2,we establish four elementary structures of the map as follows, see Fig.2.1.

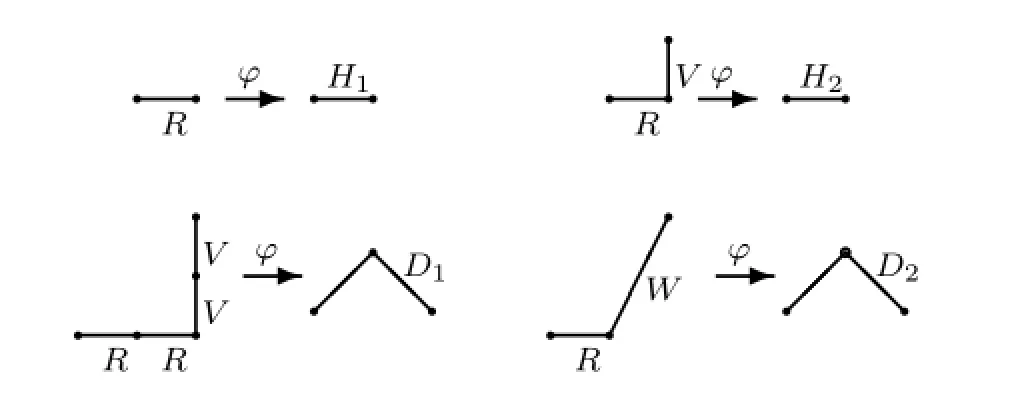
Fig.2.1 Four elementary structures

Note that any irreducible underdiagonal lattice pathforlength≥1 could be consisted of the four elementary structures.

Form≥3,we give two processes of the map based on the four elementary structures. First,we draw auxiliary lines on an irreducible underdiagonal lattice path.If there is a uniqueVon linex=i,then we draw an auxiliary line starting at the upper endpoint of theVand terminating at the left endpoint of the f i rstRit meets from northeast to southwest. Otherwise,if there are at least two consecutiveV’s on linex=i,then we denote theV’s from south to north byV1V2···Vk,fork≥2,and draw auxiliary lines starting at the upper endpoint ofV2,V3,···,Vkand terminating at the left endpoint of the f i rstRit meets from northeast to southwest,respectively.In this case,there arek−1 auxiliary lines starting at linex=i.Note that stepWcould be regarded as consecutive stepsRV V.

For any auxiliary line,the steps below it make up an irreducible underdiagonal lattice path.We label the auxiliary lines by 1,2,···,ℓaccording to the order in which they are taken.As an example,four auxiliary lines of an underdiagonal lattice path of length 6 is illustrated by dash lines in Fig.2.2.

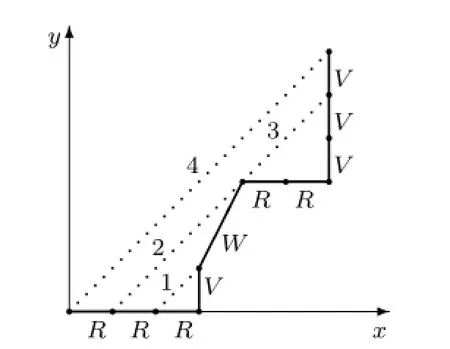
Fig.2.2 Four auxiliary lines and their labels

We now def i ne the mapφvia the following procedures.Letbe an irreducible underdiagonal lattice path.Note that iflength,then we must have, or,or,whereis an irreducible underdiagonal lattice path.Denote,whereis an irreducible underdiagonal lattice path starting at and ending on liney=x−1,for 1≤t≤ℓ.

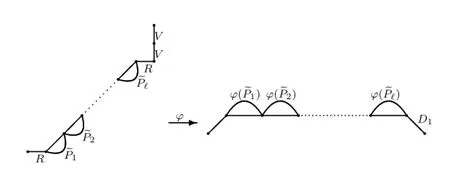
Fig.2.3

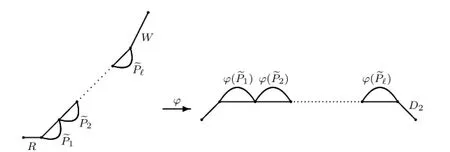
Fig.2.4

Assume thatP=P1P2···Pk,wherePiis either anRstep or an irreducible underdiagonal lattice path,for 1≤i≤k.IfPiis anR,then we letφ(Pi)beH1;ifPiis an irreducible underdiagonal lattice path,then we letφ(Pi)beφ(Pi).Finally,setφ(P)=φ(P1)φ(P2)···φ(Pk).

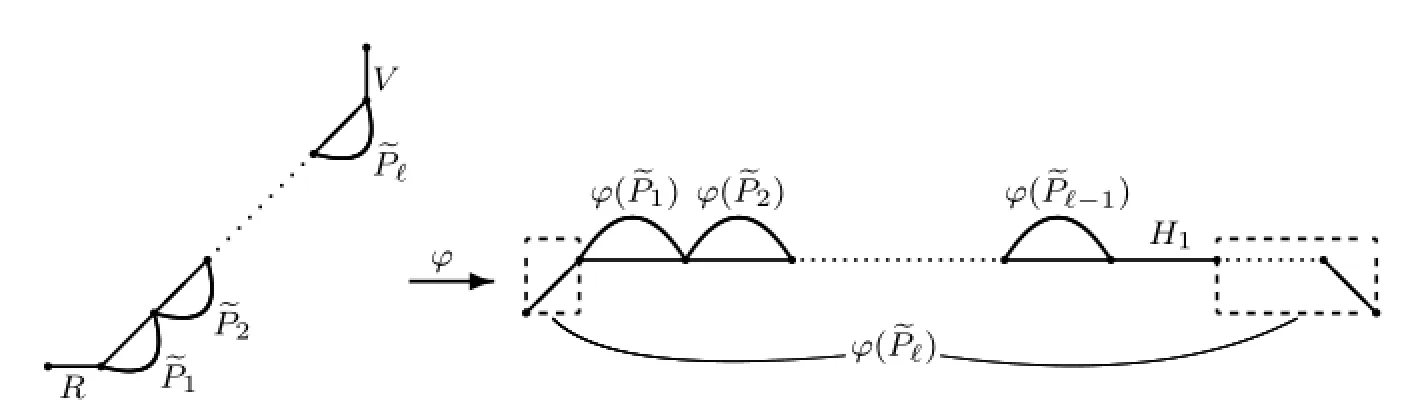
Fig.2.5

For example,an underdiagonal lattice pathPof length 16 is shown in Fig.2.6.

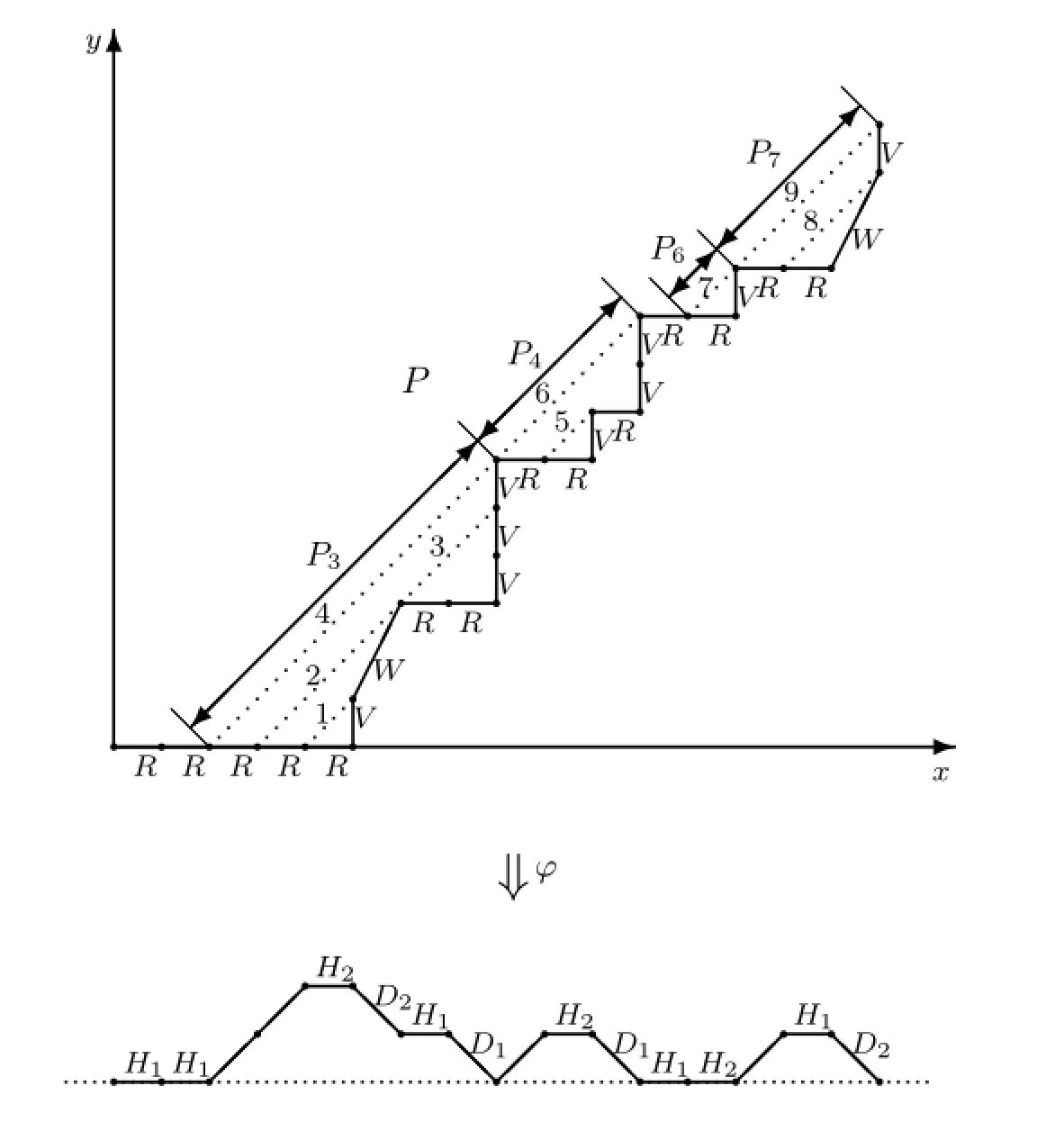
Fig.2.6 The mapφ

We draw auxiliary lines labeled by 1,2,···,9 onP.LetP=P1P2···P7,whereP1=P2=R,P3=RRRV WRRV V V,P4=RRV RV V,P5=R,P6=RV,andP7=RRWV.ForP3,there are four auxiliary lines that separate itself into four segments. LetP3=RP31P32V,whereP31=RP311WandP32=RRV V,whereP311=RV.First,we getφ(P311)=H2.Then,eliminating the auxiliary line 1,we obtainφ(P31)=UH2D2,andφ(P32)=UD1.Note that the auxiliary line 2 connects to auxiliary line 3.Thus by eliminating the auxiliary lines 2 and 3,we obtainP3=RP31P32Vandφ(P3)=UUH2D2H1D1.

Similarly,we getφ(P4)=UH2D1andφ(P7)=UH1D2.Finally,we have

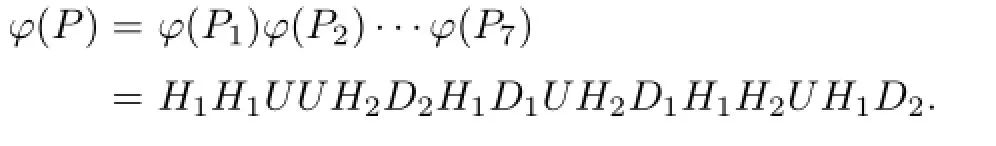
2.2 From(2,2)-Motzkin Paths to Underdiagonal Lattice Paths

An elevated Motzkin path is def i ned as a Motzkin path that does not touch thex-axis except at the origin and the destination.Bear in mind that a horizontal step on thex-axis is considered as an elevated Motzkin path.LetMbe a(2,2)-Motzkin path of lengthn. DenoteM=M1M2···Mk,whereMiis an elevated Motzkin path,for 1≤i≤k.Letψdenote the map from the set of(2,2)-Motzkin paths of lengthnto the set of underdiagonal lattice paths of lengthn.

Forlength(Mi)=1 andlength(Mi)=2,we establish four elementary structures of the map as follows:

IfMi=H1,then we setψ(Mi)=R.

IfMi=H2,then we setψ(Mi)=RV.

IfMi=UD1,then we setψ(Mi)=RRV V.

IfMi=UD2,then we setψ(Mi)=RW.

Iflength(Mi)≥3,andis an elevated Motzkin path such thatlength＜length(Mi).Then we have eitheror.Let=Mi1Mi2···Miℓ, whereMijis an elevated Motzkin path for 1≤j≤ℓ.

IfMi=and for anyj,MijH1,we set

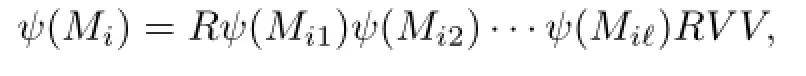
see Fig.2.7.

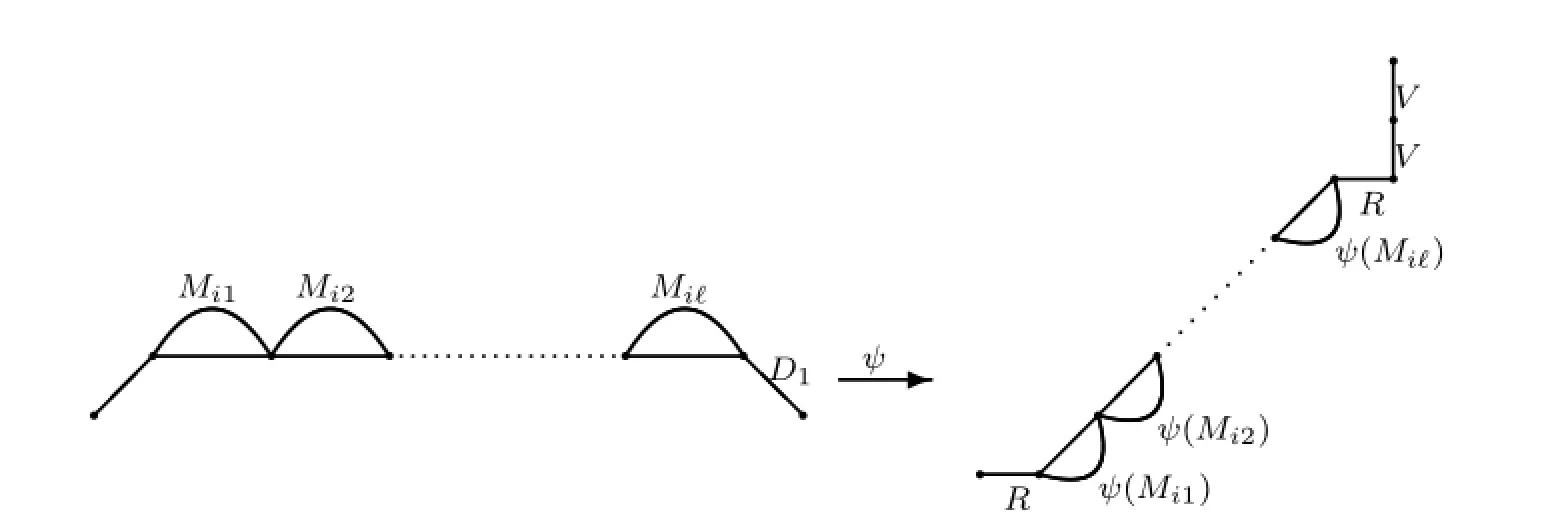
Fig.2.7Mi=andMijH1

IfMi=and there existsjwithMij=H1,then we set

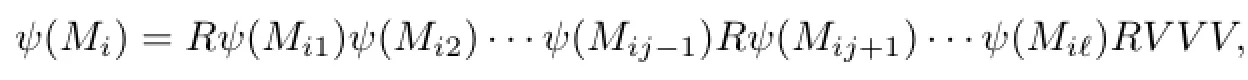
see Fig.2.8.That is to say,if there exists anyjwithMij=H1,then we letψ(Mij)inbe anRand add aVto the end of.IfMi=andMijH1for anyj,we set

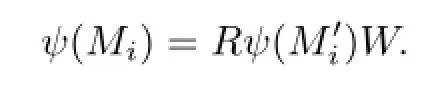
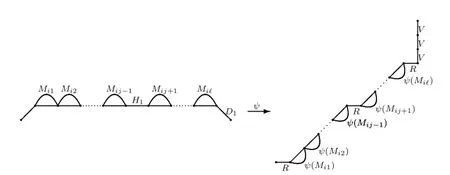
Fig.2.8Mi=andMij=H1

IfMi=and there existsjwithMij=H1,then we set

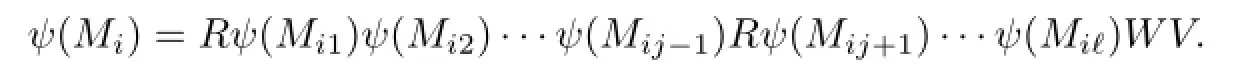
Forlength≥3,we just need to repeat the above steps and f i nally obtain

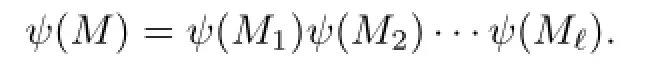
For instance,letM=M1M2M3M4in Fig.2.9,whereM1=H2,M2=UUH1UD2D1U D1H2D1,M3=UH1UD2H1D1andM4=H1.First,we easily have

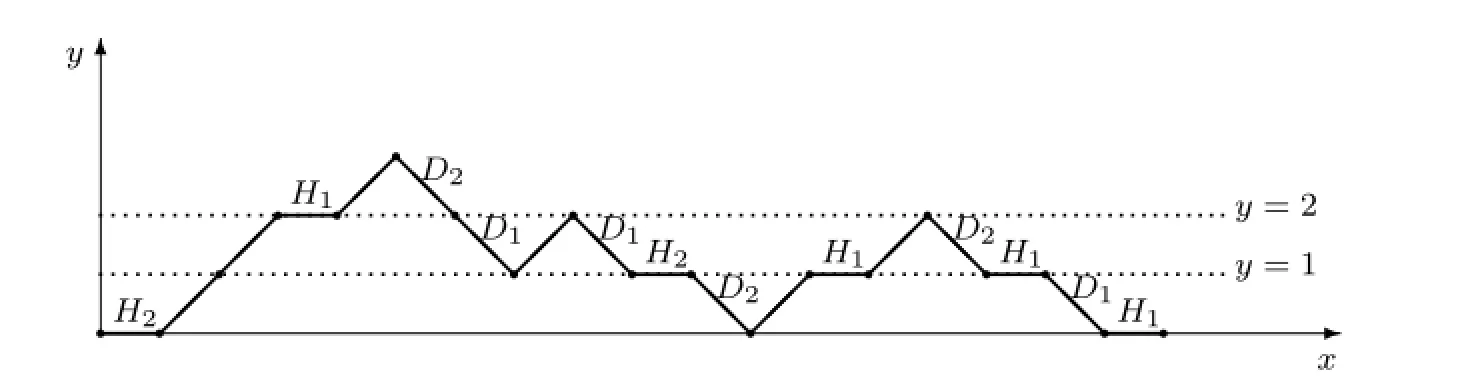
Fig.2.9M=M1M2M3M4

ForM2,letM2=UM21M22M23D1,whereM21=UH1UD2D1,M22=UD1andM23=H2.LetM21=UM211M212D1,whereM211=H1andM212=UD2.Hence

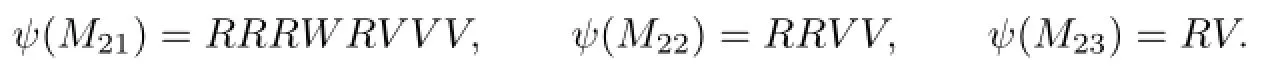
Then we get

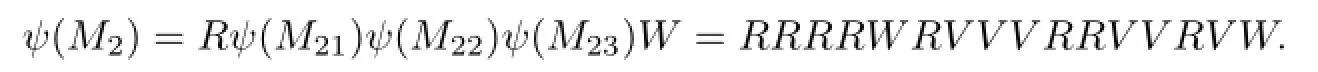
ForM3,letM3=UM31M32M33D1,whereM31=H1,M32=UD2andM33=H1. Hence

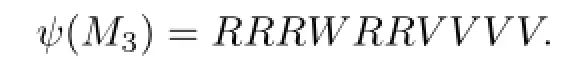
Finally,we have

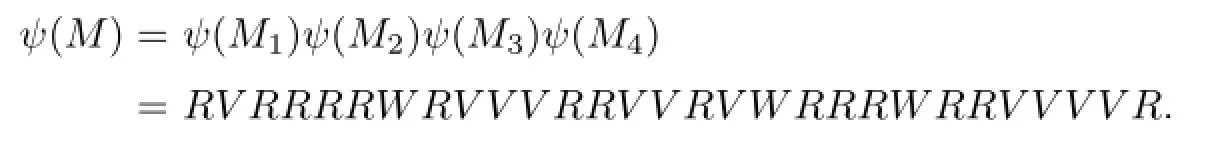
See Fig.2.10.

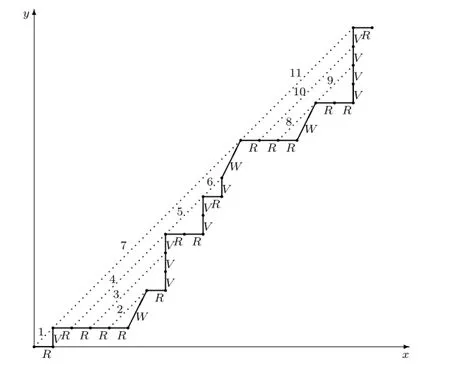
Fig.2.10ψ(M)=ψ(M1)ψ(M2)ψ(M3)ψ(M4)

It is easy to see that for any underdiagonal lattice pathPof lengthnand(2,2)-Motzkin pathMof lengthn,ifφ(P)=M,then we haveψ(M)=P,thereforeφ=ψ−1.Thus we obtain one of the main results of this paper.

Theorem 2.1There is a bijection between the set of underdiagonal lattice paths of length n and the set of(2,2)-Motzkin paths of length n.

Corollary 2.1The number of consecutive steps RV in an underdiagonal lattice path is equal to the number of step H2in the corresponding(2,2)-Motzkin path.

Corollary 2.2The number of consecutive steps RRV V in an underdiagonal lattice path is equal to the number of consecutive steps UD1in the corresponding(2,2)-Motzkin path.

Corollary 2.3The number of consecutive steps RW in an underdiagonal lattice path is equal to the number of consecutive steps UD2in the corresponding(2,2)-Motzkin path.

3 k-Motzkin Paths and(k−2)-Schr¨oder Paths

In this section,we present a bijection between the set ofk-Motzkin paths of lengthnand the set of(k−2)-Schr¨oder paths of length 2n+2 with no horizontal step at even height.

Theorem 3.1For k≥3,the number of k-Motzkin paths of length n equals the number of(k−2)-Schr¨oder paths of length2n+2with no horizontal step at even height.

Proof.LetMkndenote the set ofk-Motzkin paths of lengthn,and letMk(x)denote the generating function of the number ofMkn.LetMk∈Mkn.By the f i rst return decomposition,one can easily see thatMkis a single point,or it starts with a level step,or it starts with an up step.See Fig.3.1 for an illustration.That is to say

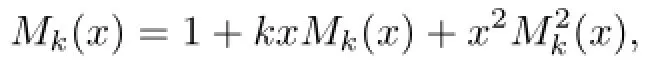
which yields

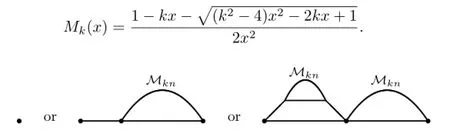
Fig.3.1 Three possible cases ofMk

LetSkndenote the set ofk-Schr¨oder paths of length 2n+2 with no horizontal step at even height,and letSk(x)denote the generating function of the number ofSkn.Letdenote the set ofk-Schr¨oder paths of length 2n+2 with no horizontal step at odd height,and letdenote the generating function of the number of.LetSk∈Sknand. By the f i rst return decomposition,one can see thatSkis a single point,or it starts with an up step,andis a single point,or it starts with a level step,or it starts with an up step. See Fig.3.2.Then

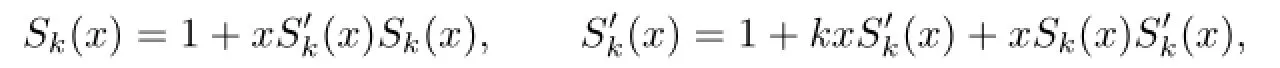
which yields

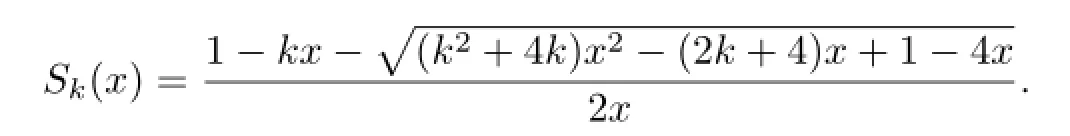
Fig.3.2 Possible cases ofSkand

Interchangingktok−2,we get

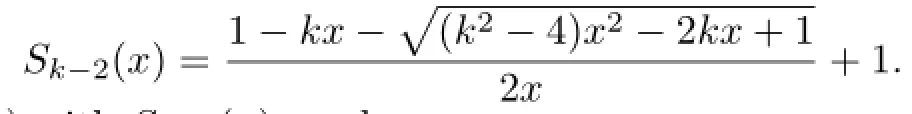
By comparingMk(x)withSk−2(x),we have

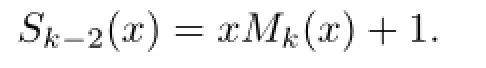
Now we give a combinatorial proof of Theorem 3.1.

For anyk≥3,letHidenote a horizontal step ofk-Motzkin paths with colori,and lethjdenote a horizontal step ofk-Schr¨oder paths with colorj,fori=1,2,···,k,andj=1,2,···,k−2.

Theorem 3.2For k≥3,there exists a bijection between the set of k-Motzkin paths of length n and the set of(k−2)-Schr¨oder paths of length2n+2with no horizontal step at even height.

Proof.We shall construct a mapτfromMkntoSkn.Given ak-Motzkin pathMkof lengthn,we can obtain a lattice pathτ(Mk)via the following procedures.

(1)Setτ(H1)=h1,τ(H2)=h2,···,τ(Hk−2)=hk−2,τ(Hk−1)=udandτ(Hk)=du.

(2)Setτ(U)=uu.

(3)Setτ(D)=dd.

(4)Add austep at the front,and add adstep at the end.

See Fig.3.3 for an illustration.It is obvious thatτ(Mk)is a(k−2)-Schr¨oder path of length 2n+2 with no horizontal step at even height.The map is reversible,see Fig.3.3. Given a(k−2)-Schr¨oder pathSkof length 2n+2 with no horizontal step at even height,it is apparent thatτ−1(Sk)is ak-Motzkin path of lengthn.

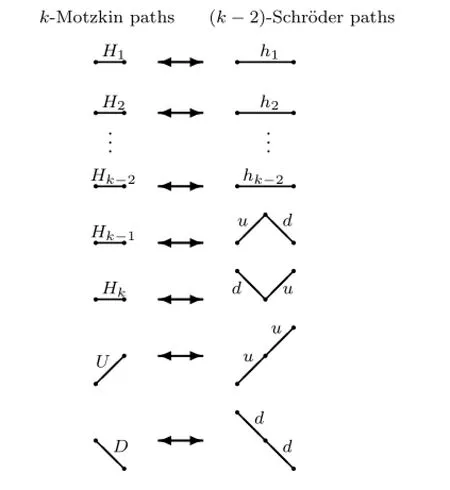
Fig.3.3 The mapτ

Note that ak-Schr¨oder path of length 2n+2 without any horizonal stepsH’s is essence a Dyck path of length 2n+2.Then by Theorem 3.1,we obtain the well-known bijection between the set of Dyck paths of length 2nand 2-Motzkin paths of lengthn−1.

[1]The OEIS Inc.,The On-Line Encyclopedia of Integer Sequences,http://oeis.org.

[2]Merlini D,Rogers D G,Sprugnoli R,Verri M C.Underdiagonal lattice paths with unrestricted steps.Discrete Appl.Math.,1999,91:197–213.

[3]Chen W Y C,Wang C J.Noncrossing linked partitions and large(3,2)-Motzkin paths.Discrete Math.,2012,321:1918–1922.

[4]Woan W.A recursive relation for weigted Motzkin sequences.J.Integer Seq.,2005,8:Article 05.1.6.

[5]Woan W.A relation between restricted and unrestricted weigted Motzkin paths.J.Integer Seq.,2006,9:Article 06.1.7.

[6]Barnabei M,Bonetti F,Silimbani M.Restricted involutions and Motzkin paths.Adv.in Appl. Math.,2011,47:102–115.

[7]Ding Y,Du R R X.Counting humps in Motzkin paths.Discrete Appl.Math.,2012,160: 187–191.

[8]Sulanke R A.Bijective recurrences for Motzkin paths.Adv.in Appl.Math.,2001,27:627–640.

[9]Wang Y,Zhang Z H.Combinatorics of generalized Motzkin numbers.J.Integer Seq.,2015, 18:Article 15.2.4.

[10]Yan S H F.From(2,3)-Motzkin paths to Schr¨oder paths.J.Integer Seq.,2007,10:Article 07.9.1.

[11]Shapiro L W,Wang C J.A bijection between 3-Motzkin paths and Schr¨oder paths with no peak at odd height.J.Integer Seq.,2009,12:Article 09.3.2.

[12]Deutsch E,Shapiro L W.A bijection between ordered trees and 2-Motzkin paths and its many consequences.Discrete Math.,2002,256:655–670.

tion:05C38,05A19

A

1674-5647(2017)02-0149-11

10.13447/j.1674-5647.2017.02.07

Received date:June 8,2016.

Foundation item:The NSF(11601020,11501014)of China,Organization Department of Beijing Municipal Committee(2013D005003000012),Science and Technology Innovation Platform-Business Project 2017.

E-mail address:chenzjst@163.com(Chen Z J).