On Fundamental Group of a Certain Class of Welded Knots
2017-05-11LIZHIGUOLEIFENGCHUNCHENZHIANDWUJIE
LI ZHI-GUOLEI FENG-CHUNCHEN ZHIAND WU JIE
(1.Department of Mathematics,Dalian University of Technology,Dalian,Liaoning,116024)
(2.School of Science,Hebei University of Technology,Tianjin,300401)
(3.Department of Mathematics,Hefei University of Technology,Hefei,230009)
(4.Department of Mathematics,National University of Singapore,Singapore)
On Fundamental Group of a Certain Class of Welded Knots
LI ZHI-GUO1,2,LEI FENG-CHUN1,CHEN ZHI3AND WU JIE4
(1.Department of Mathematics,Dalian University of Technology,Dalian,Liaoning,116024)
(2.School of Science,Hebei University of Technology,Tianjin,300401)
(3.Department of Mathematics,Hefei University of Technology,Hefei,230009)
(4.Department of Mathematics,National University of Singapore,Singapore)
In this paper,a certain class of welded knotsK2nis considered.By calculating the commutators subgroup of fundamental groupGnof welded knotK2n,n∈Z+,we show that these welded knots are not equivalent to each other and they are all not classical knots.Secondly,we study some properties ofGnand obtain thatGnis linear,residually f i nite and Hopf i an.
welded knot,fundamental group,Dihedral group,linear group
1 Introduction
In 1996,Kauf f man[1]introduced the notion of a virtual knot,which is motivated by the study of knots in a thickened surface and abstract Gauss codes.Goussarovet al.[2]showed that virtual knot theory is very ef f ective and natural to study in relation to f i nite type invariants of knots.According to[2],two classical knot diagrams represent the same knot type if and only if they represent the same virtual knot type,which is also proved by Kauf f man[1]by using the notion of involution quandle.Hence the concept of virtual knot is a generalization to classical knot in three space.
Several invariants in classical knot theory can be naturally extended to virtual knot, including the Jones polynomial and knot groupG(K)(see[1]).However,the Jones polynomial is not well-def i ned for welded knot.Fish and Keyman[3]def i ned a Jones polynomial invariant for fused links by changing the base ring Z[t±1]to some quotient ring.But for welded knot,this Jones polynomial invariant is still trivial.As far as we are concerned,littleis known about polynomial invariant for welded knot theory.Hence,for welded knot theory, the fundamental group of a welded knot is the main invariant so far.
In 2000,Silver and Williams[4]gave an example of virtual knot which is not a classical knot by discussing the commutators subgroup of its fundamental group.
In this paper,we consider a certain class of welded knot whose diagram was shown in Fig.1.1,which is a generalization of the example of Silver and Williams,and denote this welded knot byK2n.
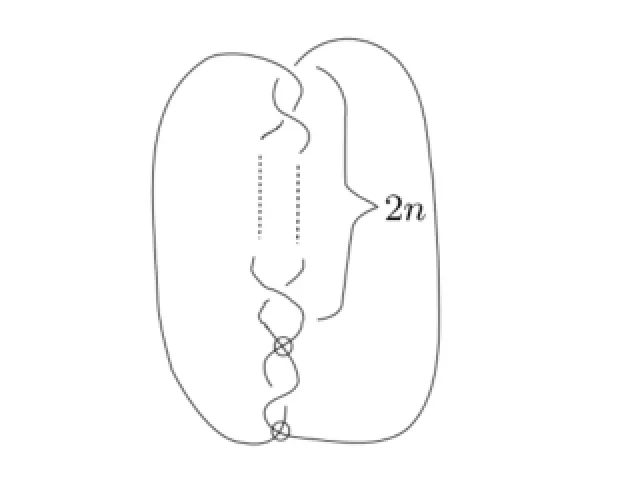
Fig.1.1 The welded knotK2n
This welded knot can be regarded as by f l anking one classical crossing from torus knotT(2n+1,2)by virtuals and switching its crossing.For convenience,We denote the fundamental group ofK2nbyGn.By calculating the fundamental groups of these welded knots for dif f erentn,we prove that they are pairwise dif f erent and they are all not classical knots. Main results are the following:
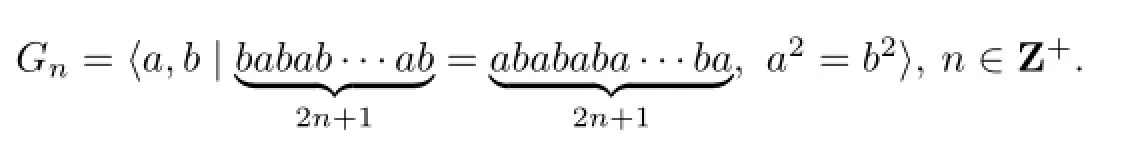
Lemma 1.2[Gn,Gn]~=Z2n+1,n∈Z+.
Theorem 1.1K2mK2nas welded knot if mn(m,n∈Z+).
Corollary 1.1K2nis not a classical knot for n∈Z+.
This paper is organized as follows.In Section 2,we recall some def i nitions about virtual and welded knot theory.In Section 3,we give the presentation of the fundamental group of welded knotK2n.By calculating the commutators subgroup of the fundamental groupGnofKn,we show thatKnis dif f erent toKmifmis dif f erent ton.Finally,forGnis something like between Artin group and Coxeter group,we study some properties ofGnand obtain thatGnis a linear group,residually f i nite and hopf i an.
2 Virtual Knot and Welded Knot Theory
A shape virtual knot diagram is a generic immersion of the circle into the plane,with double points representing classical crossing and virtual crossings.The branches of a classicalcrossing are divided into overpass and underpass in a usual way.A virtual crossing is represented by two crossing arcs with a small circle placed around the crossing point.
Two virtual knot diagrams are shape equivalent under ambient isotopy and some types of local moves(generalized Reidemeister moves):Classical Reidemeister moves(R1–R3), virtual Reidemeister moves(V1–V3)and mixed Reidemeister moves(V4)(see Fig.2.1).A shape virtual knot is an equivalence class of a virtual knot diagram.
If allowed the forbidden moveF1(see Fig.2.1),then one can obtain the theory of shape welded links whose interest is growing up recently because of the fact that the welded braid counterpart can be def i ned in several equivalent ways(for instance in terms of conf i guration spaces,mapping classes and automorphisms of free groups,see[5]).If allowed two forbidden moves,one can get the theory called shape fused knot or shape unwelded knot which is a trivial theory,since any knot in this theory is equivalent to the trivial knot(see[6]–[7]).
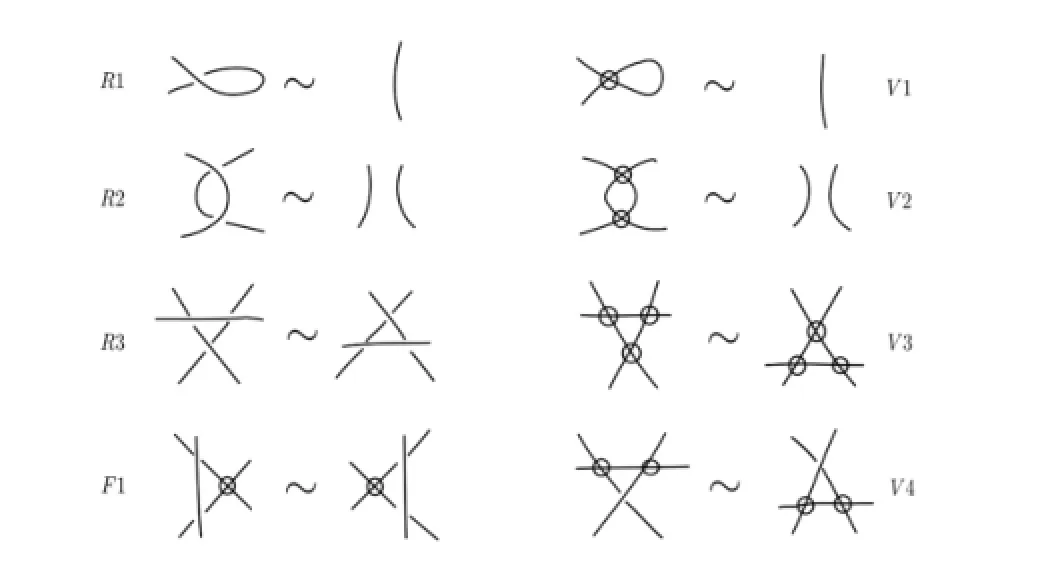
Fig.2.1 Generalized Reidemeister moves for welded knot theory
A virtual knotKcan be formally associated with a groupG(K)through a Wirtinger presentation obtained from any diagram for the knot.The groupG(K)has one generator for each arc,which starts and ends at under-crossings,and one relation for each classical crossing,just as in Fig.2.2.In this construction,we ignore the virtual crossing ofK.This construction was f i rst introduced by Kauf f man[1].G(K)is invariant under all generalized Reidemeister moves and hence is an invariant of a virtual knot.The knot groupG(K)does not change under the forbidden moveF1.So the knot groupG(K)is an invariant of a welded knot.For convenience,we still call the knot groupG(k)the fundamental group of the welded knotK.It is still an open problem whetherG(K)detects the trivial knot among welded knots.
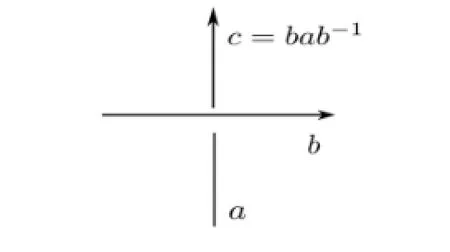
Fig.2.2 Relation at a crossing
3 Presentations of Fundamental Groups for Welded Knot K n
LetGnbe the group of welded knotK2n.We label the diagramDnofK2nas in Fig.3.1.
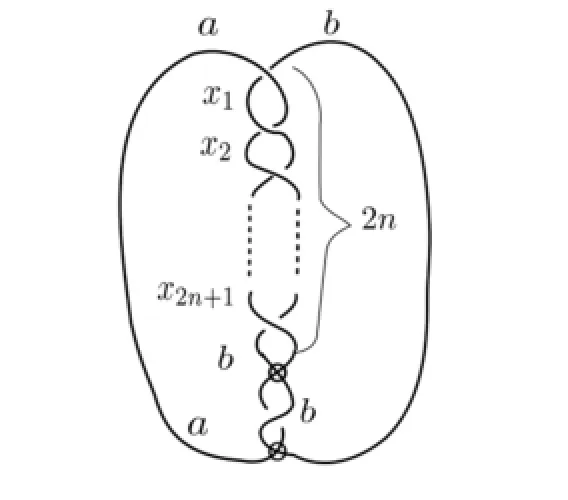
Fig.3.1Gnand their generators
Proposition 3.1Let Gnbe the welded knot group of K2n,then
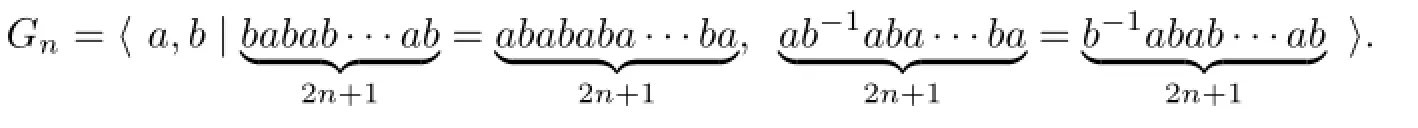
Proof.By Wirtinger presentation,we have
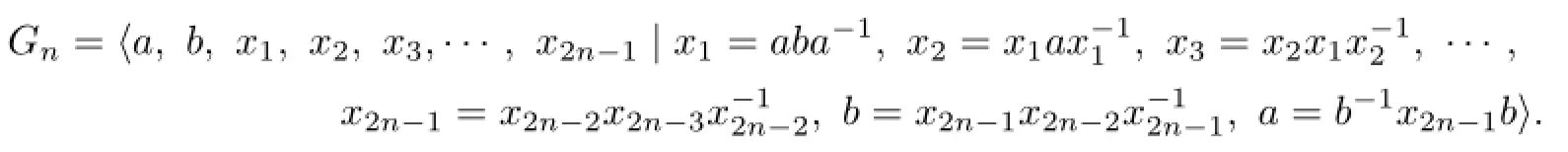
By the relations ofGn,we have
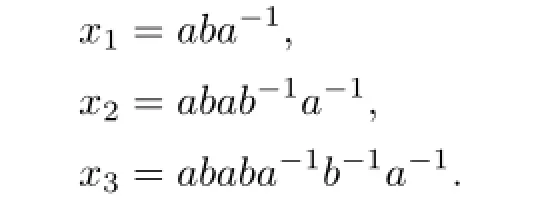
If we suppose

then it is easy to be obtained that
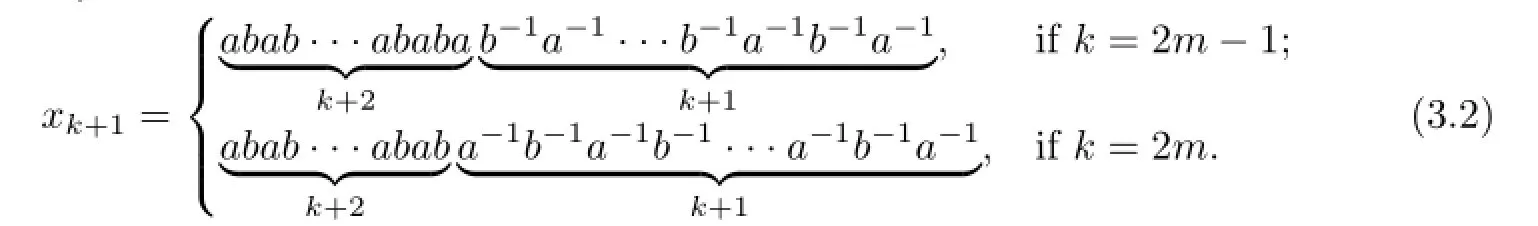
Hence,by induction we have

Thus,the last two relations ofGnis changed to the followings:

Therefore,we obtain

Proof of Lemma 1.1By Proposition 3.1 and Tietze transformations,we haveGn
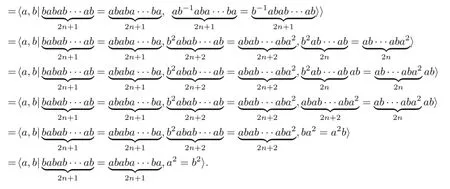


Proof of Lemma 1.2By Lemma 1.1,we have
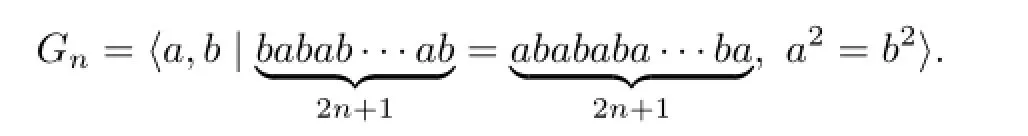
Letc=a2=b2.Thencis a central element inGn.Let
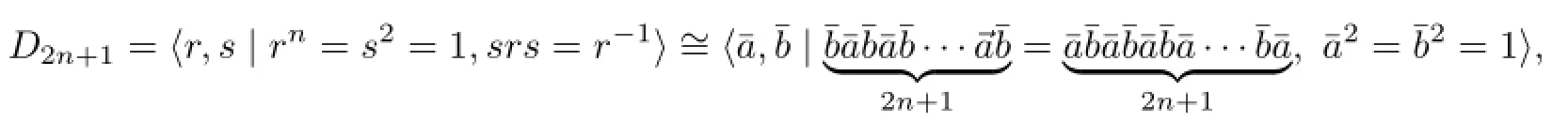
where the isomorphim is given by the Tietze transformation by replacing the two generators withor from the coxeter system of the Dihedral groups.
From the presentations ofGnandD2n+1,we get an epimorphismπfromGntoD2n+1:
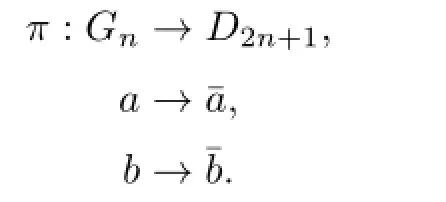
It is easy to see that kerπ={ci,i=1,2,···}~=Z.The epimorphismπinduce an epimorphism between their commutators subgroups:
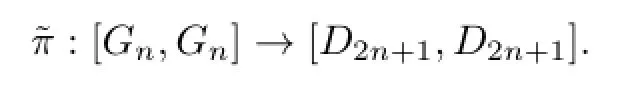
Corollary 3.1(Gn)is the center of the group G.
Corollary 3.2There is an exact sequence
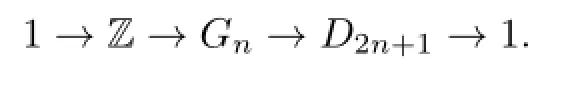
Remark 3.1From the Corollary 3.2,we know thatGnis a central extension of Z by the Dihedral groupD2n+1.
Proof of Theorem 1.1By Lemma 1.2,we know that[Gn,Gn]Z2n+1.SoGnGm().Because welded knot group is an invariant of welded knot,we have
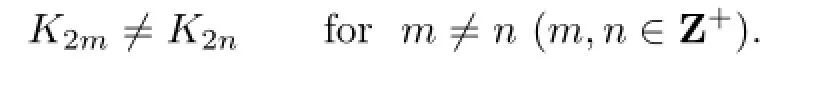
Lemma 3.2[8]The commutator subgroup of any classical knot group is free whenever it isfi nitely generated.
By Lemmas 1.2 and 3.2,we obtain Corollary 1.1.
4 Some Properties on the Group Gn
Proposition 4.1The group Gnis a solvable group,n∈Z+.
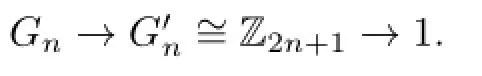
Lemma 4.1[9]Let H be a subgroup of f i nite index m in the group G and ϕ be a monomorphism ofintoGL(n,F).Then there exists a monomorphism ϕ1of G intoGL(mn,F).If H is normal in G,ϕ is completely reducible and eithercharF=0orcharF is prime to m, then ϕ1is also completely reducible.
Proposition 4.2Gnis a linear group,n∈Z+.
Proof.Since Z is a linear group,by Corollary 3.4 and Lemma 4.2,the result is established.Def i nition 4.1A group G is residually f i nite if for any nontrivial element g∈G there exists a f i nite-index subgroup N◁G such that g/∈N.
Def i nition 4.2A Hopf i an group is a group G for which every epimorphism G→G is an isomorphism.Equivalently,a group is Hopf i an if and only if it is not isomorphic to any of its proper quotients.
Lemma 4.2[10]If R is f i nitely generated integral domain,then GL(n,R)is a residuallyfi nite group.
Lemma 4.3[11]Every subgroup of a residually f i nite group is residually f i nite.
Lemma 4.4[12]A f i nitely generated residually f i nite group is a Hopf i an group.
By Proposition 4.2 and Lemmas 4.2–4.4,we have
Corollary 4.1Gnis residually f i nite and Hopf i an for n∈Z+.
Actually,we can transformate every element ofGninto one of the following four normal forms:abab···abci,abab···abaci,baba···baci,baba···babci(i∈Z).For example,a5b−3a4b2=ac2bc−2c2c=abc3.
We can list all elements ofGnas follows:
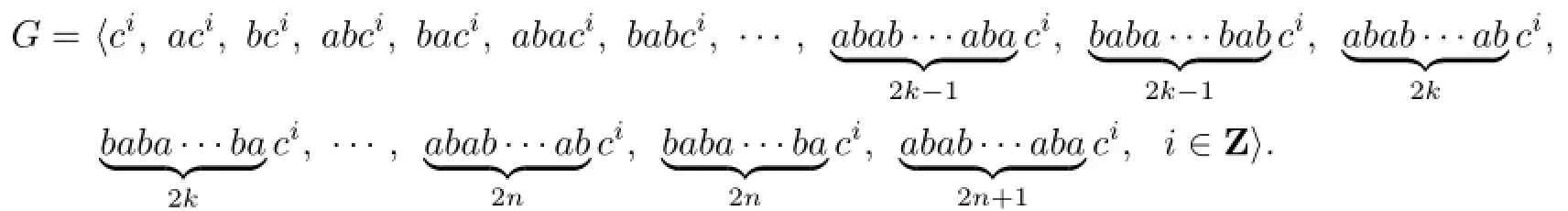
The groupGnhas the following conjugate classes:

From above arguments,it is easy to show the following theorem:
Theorem 4.1Gnhas solvable word problem and conjugacy problem.
Given a propertyP,the groupGis said to be virtuallyPif there is a f i nite index subgroupH≤Gsuch thatHhas propertyP(see[13]).
Proposition 4.3The group Gnis virtually abelian,virtually nilpotent,virtually torsion free and virtually free.
Proof.Gnhas a subgroup Z with f i nite index 4n+2.The subgroup Z is abelian,nilpotent, torsion free and free.So the results are established.
[1]Kauf f man L H.Virtual knot theory.European J.Combin.,1999,20(7):663–690.
[2]Goussarov M,Polyak M,Viro O.Finite-type invariants of classical and virtual knots.Topology, 2000,39(5):1045–1068.
[3]Fish A,Keyman E.Jones polynomial invariants.J.Knot Theory Ramif i cations,2006,15(3): 339–350.
[4]Silver D S,Williams S G.Virtual Knot Groups.In Knots in Hellas’98 Delphi,vol.24 of Ser. Knots Everything.River Edge,NJ:World Sci.Publ.,2000,440–451.
[5]Bardakov V G,Bellingeri P.Groups of virtual and welded links.J.Knot Theory Ramif i cations, 2014,23(3):1450014.
[6]Kanenobu T.Forbidden moves unknot a virtual knot.J.Knot Theory Ramif i cations,2001, 10(1):89–96.
[7]Nelson S.Unknotting virtual knots with gauss diagram forbidden moves.J.Knot Theory Ramif i cations,2001,10(6):931–935.
[8]Burde G,Zieschang H.Knots.vol.5.Berlin:Walter de gruyter,2003.
[9]Wehrfritz B.Inf i nite Linear Groups:An Account of the Group-theoretic Properties of Inf i nite Groups of Matrices,vol.76.New York:Springer Science and Business Media,2012.
[10]Malcev A I.On the faithful representation of inf i nite groups by matrices.Mat.Sb.,1940,50(8): 405–422.
[11]Ceccherini-Silberstein T,Coornaert M.Cellular Automata and Groups.New York:Springer, 2009.
[12]Neumann H.Varieties of Groups,vol.37.New York:Springer Science and Business Media, 2012.
[13]Schneebeli,H.R.On virtual properties and group extensions.Math.Z.,1978,159(2):159–167.
tion:57M25,57M27
A
1674-5647(2017)02-0177-08
10.13447/j.1674-5647.2017.02.09
Received date:Sept.19,2016.
Foundation item:The NSF(11329101,11431009,11301135 and 11471245)of China.
E-mail address:zhiguolee@mail.dlut.edu.cn(Li Z G).
杂志排行
Communications in Mathematical Research的其它文章
- Monomial Derivations without Darboux Polynomials
- The Invariant Rings of the Generalized Transvection Groups in the Modular Case
- Two Bijections on Weighted Motzkin Paths
- Uniqueness in Determining a Ball with a Single Incoming Wave
- Growth of Solutions to Higher Order Dif f erential Equation with Meromorphic Coeffi cients
- A New Characterization on g-frames in Hilbert C∗-Modules
