航空叶片型面三坐标检测技术现状及发展趋势*
2017-05-11
(电子科技大学机械电子工程学院,成都 611371)
航空发动机是一种高度复杂和精密的热力机械,主要为航空器提供飞行动力,被誉为飞机的“心脏”,又被称为“工业之花”,直接影响着飞机的可靠性及经济性,是一个国家工业实力的重要体现。航空叶片是发动机的核心部件之一,也是涉及发动机安全性能的关键动部件,发动机需要通过叶片对空气进行压缩和膨胀,其曲面形状和制造精度很大程度上决定了发动机的推进效率[1]。因此在叶片制造过程中,必须重视其型面的质量控制,通过科学有效地应用叶片检测技术,能够有效保障叶片型面制造精度,最终保证复杂气动外型的高性能特性。
叶片通常为薄壁、大扭曲、批量生产的精密部件,其检测存在一系列难点:(1)检测精度要求高,通常要求微米级测量;(2)对检测效率要求较高,须满足生产要求;(3)由于叶片安装楔型面小,其测量过程中装夹定位和基准建立的误差较大;(4)叶片测量数据的处理与分析复杂,综合评定难度较大[2]。现有的叶片型面检测方法基本可分为接触式检测与非接触式检测两类。接触式测量是指通过传感器测头与产品接触的方式来测量产品表面点的坐标位置;非接触式测量主要是指基于光学、磁学等领域的基本原理,利用相关物理模拟量来得到产品表面数字信息的方法,如激光测量等。叶片测量方法中接触式的三坐标测量技术目前相对于其他测量方式具有更高的可靠性和测量精度,被广泛应用在叶片型面的质量控制中。
如何实现叶片高效、高精度、人性化的测量,解决好检测过程中的一系列技术难题,对提升叶片制造品质和解决数字化工厂的管控效能具有重要价值,也对我国航空航天及其他高端制造行业的制造品质管控具有重要意义。
1 航空叶片三坐标检测技术及设备
坐标测量是在20世纪中期发展起来的一种测量新技术,其主要原理是通过数字测量设备将被测几何元素的测量转化成对部分关键点集的测量,而后再采用数据建模等分析手段来实现对测量对象的评定[3]。国外工业发达国家在坐标测量机(Coordinate Measuring Machine,CMM)领域具有明显的优势,全球著名的坐标测量设备制造商均出自国外,如MAHR、Zeiss、Hexagon等。图1所示为基于Hexagon的三坐标测量机对叶片的测量过程,该CMM配置了专业叶片检测夹具,能够一次性对多个叶片进行测量,大幅提升了检测的效率。
在叶片三坐标检测领域,高效、高精度的测量方法以及叶片专用的测量与分析软件一直是研究的重点和热点。测量的效率和精度很大程度上是由测头系统所决定的,接触式测头又分为触发式与扫描式两大类,其中扫描式测头由于测量效率高、测点密集等特点,多用于有形状和轮廓要求零件的测量,也是目前通过CMM对叶片测量时最常用的测头。近年,为适应车间恶劣的工作环境,MARPOSS公司研发了具有高稳定性和高可靠性Mida™系列测头。英国Renishaw公司也于2015年推出了高精度的五轴测量系统REVO-2,大幅度降低了坐标测量机在高速测量时的动态误差,提高了检测结果的准确性,且相对于传统的依靠分度头所实现的五轴叶片测量系统而言[4],其在测量效率和精度方面具有十分明显的优势。此外,研制高精度的扫描式测头的企业还有日本的Metrol、德国的Kapp和Leitz等单位。

图1 GLOBAL Silver系列的三坐标测量机Fig. 1 CMM of GLOBAL Silver series
为了实现航空叶片高效测量与准确评定,国外企业在叶片专用测量软件研制方面进行了深入研究,目前可谓是硕果累累,仅Renishaw公司就开发了3套叶片测量专用软件,分别是叶片快速扫描测量软件APEXBlade™、叶片型面分析软件MODUS™以及叶片逆向工程软件SurfitBlade™,该系列产品突破了传统分段测量的方式,能够快速、全面地对整个叶片型面进行检测和分析。目前国内应用较多的是Hexagon公司的叶片测量软件包Blade,该软件基于等高测量法对叶片进行检测,通过简单的参数设置便能完成复杂的测量规划,能够准确地分析叶片各项误差,且具有多样化的检测报告输出模块,不过该软件主要以叶片等高截面为分析单元,在整体型面误差以及误差可视化方面还略有不足。此外,Zeiss公司开发了BLADE PRO软件,该软件可对非等比例长度误差进行分析,能够完成对叶片前、后缘等关键区域几何质量的评定。AEH公司也研发了叶片测量软件AC-VANE,该软件以数据库为平台对叶片的关键测量信息进行了统一有效的管理,不仅提高了测量效率,还为叶片后续的跟踪管控提供了基础对比数据。此外,Geomagic、Wenzel等公司也开发了各自的叶片分析专用模块。
国产CMM的研制始于20世纪70年代,目前主要生产厂商有航空工业北京精密机械研究所、北京机床研究所等单位,虽然在可靠性、准确性等性能方面稍逊于国外设备,但由于在价格和售后方面的优势,仍具有一定的市场占有率。在接触式测头研制领域,哈尔滨先锋机电是国内技术相对成熟的厂商,其推出的TP系列和EP系列的测头在国产CMM中有着大量的应用,此外国内研制精密测头的单位主要还有中国航天科工集团第303所、北京机床研究所等。从总体而言,国内在测头研制领域远不及国外先进水平,尤其是在精密扫描测头和多轴测座系统研制方面。
我国在叶片类专用三坐标测量软件方面还处于探索起步阶段,虽然市场尚无成熟的自主开发的商用叶片测量软件系统,不过在分析软件方面还是取得了一定的成果。台湾中央大学开发的Rev CAD软件[5]能够基于坐标测量数据对航空叶片型面进行分析和评定,但其仅能进行二维层次的评价,无法实现可视化程度更高的三维偏差分析。北京航空航天大学席平等[6]基于UG平台开发了一套能够对叶片型面进行误差评定的系统,该系统能够显著提高叶片的误差检测速度和分析质量,但其功能单一,且在检测报告输出方面并不完善,无可视化的测量截面信息,如截面的理论轮廓、实际轮廓、公差带、超差区域等信息。国内首个功能较完善的叶片测量分析系统是西北工业大学陈志强等[7]基于叶片CMM测量数据开发的航空叶片自动评价软件系统,该系统可对叶片的各关键评价参数进行准确地提取,并且能够进行叶片三维偏差分析,且具有多样化的检测报告输出功能,但与国外相应软件相比,该系统的模型配准方式以及部分关键参数提取算法单一,同时软件的可交互性仍有待提高。近期,电子科技大学开发了针对叶片型面进行误差评定与逆向重构的软件系统,并配套相关企业的CMM开展了系列工程化的应用,该系统不仅能够准确地提取叶片型面的各特征参数与位置度误差,还能基于实际重构模型对叶片型面加工误差进行可视化分析。虽经过多年的发展,但国内叶片测量软件在测量过程的规划与控制方面功能仍较欠缺,叶片分析评定软件大多还处于起步阶段,且多数软件适应性较低,对叶片大小和扭曲程度较为敏感,并且分析结果的准确性与国外同类软件相比仍有一定差距,因此这些分析软件在国内航空叶片的精密测量中并没有得到较多的推广和应用。
综上所述,叶片三坐标检测技术及设备在国外发展已较为成熟,商业化的精密三坐标测量设备与叶片测量软件的可选性高,并广泛应用于航空叶片质量的检测中。目前国内研制的坐标测量设备在可靠性、重复性方面与国外仍有一定差距,且尚无成熟的叶片专用的坐标测量软件,在叶片坐标测量评价分析软件方面,普遍智能化程度低、通用性差、功能单一且种类较少,并且多数仍处于试验阶段,因此国内在叶片的高精密坐标测量时仍主要采用国外设备及相应软件系统。
2 叶片三坐标检测关键技术研究进展
在叶片三坐标检测的过程中,其关键技术主要包括叶片的测量规划、测量定位、数据处理分析和质量评定4个方面。
2.1 叶片坐标测量规划技术
测量规划的目的是得到完整的、合理可行的测量路径,且是影响测量效率与评定结果准确性的重要因素。由于叶片通常为扭曲薄壁件,在对其测量的过程中测头易受到前后缘的干扰,从而产生干涉点,这也是目前在叶片制造企业中存在的典型问题,因此目前叶片坐标测量规划的关键主要仍在测点布局和干涉检查方面。
目前测点规划主要在叶片等高截面型线上展开,测点的疏密应尽可能与被测曲面曲率的变化一致。Pahk等[8]提出了弦长准则规划方法,通过控制相邻两点所构成的弦线与截面线之间的最大距离来实现采点密度跟随曲面曲率变化,但该方法在相对平坦的区域易出现采点密度过低的情况,鉴于此,I. Ainsworth等[9]将最小样本密度准则与弦长准则相结合,通过设定相邻点间的最大允许距离来实现对采点密度的控制,弥补了弦长准则的缺陷,此外,还可通过控制型线切线方向变化的速度来实现测点规划。国内学者还提出了基于容差控制的规划方法[10],结合曲率和加工误差进行规划,使得测点分布更为科学合理,提高了评定结果的准确性。针对测点等高线规划方法可能造成测量路径线断裂的问题,蔺小军等[11]提出了基于流道线的测点规划方法,将气流经过叶片型面的近似路线作为测量截面,然后再根据截面型线曲率进行测点规划,等高法测量与流道线测量如图2所示,通过对其分析可知,基于流道线所获取的截面型线较等高截面型线更符合叶片曲面构造方式,更适用于逆向工程中大扭曲叶片的实体造型,而基于等高截面的测量方法则更利于叶片型面质量的评定。
干涉检查操作是为了检验叶片测量路径的可行性,对检测出的碰撞点通过调整检测路径或测头姿态进行规避。干涉检查方法可分为静态检测和动态检测两类。静态检查主要是验证测点的可测性,又可根据干涉判断方式的不同,将其分为距离判断和求交判断两类,如文献[12]中采用层次八叉树方盒近似模型,通过模型之间求交来判断测头是否发生干涉。动态检测主要是判断测头在测点间移动时以及空走时是否出现碰撞,根据检测方式可分为离散和连续碰撞检测两类。离散算法按预设步长对采样处进行静态干涉检测来判断碰撞,存在遗漏碰撞点的可能。连续碰撞检测一般涉及到四维时空问题的精确建模,其中应用较多的是扫描体法,该方法虽不会遗漏碰撞点,但由于缺少即时信息可能出现不发生碰撞时仍会检测到相交的情况,如文献[13]中,基于B-rep模型运用扫描体求交算法实现了叶片的动态碰撞检测。检测效率是决定碰撞检测算法优劣的关键性因素,目前提高效率的主要方法在于简化检测模型与减少干涉检测时运算的几何模型数目两个方面。如Lin等[14]提出将离散碰撞检测算法与扫描体包围盒相结合的方法,简化了求交模型,通过基本几何元素之间的相交检查来完成碰撞检测,极大地提升了检测效率;刘达新等[12]在此基础上,提出了利用轴向包围盒的对边界过滤的方法,减小了求交计算的复杂度。可以看出,目前叶片测量路径动态干涉检测结果的准确度还有待提高,相交检测计算的复杂度仍然很高,导致计算效率低下,因此目前叶片测量路径可行性的验证方法仍有待进一步的优化。
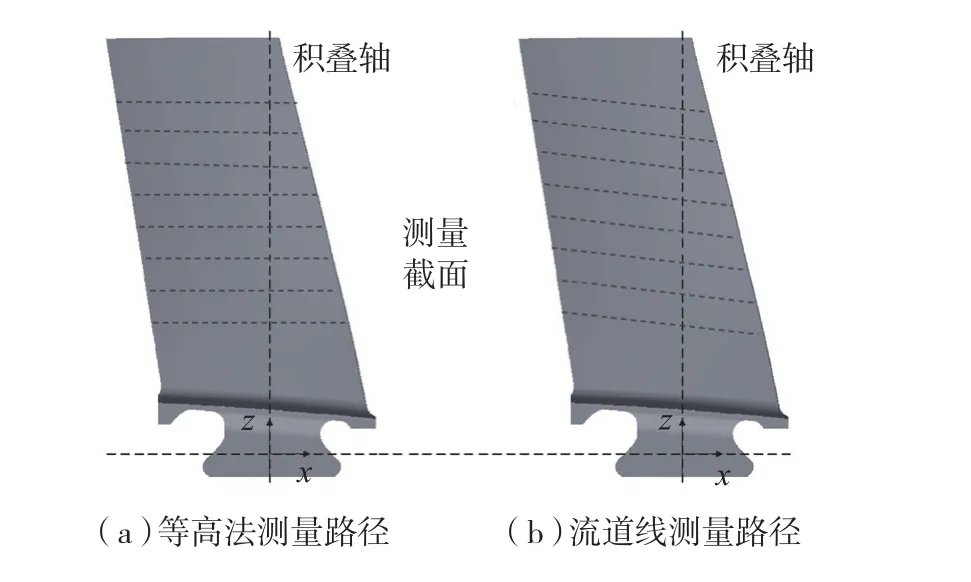
图2 叶片测量路径Fig.2 Measuring path of blade
2.2 叶片坐标测量定位技术
叶片精准快速的定位是高效、高精度检测的前提,定位的精度直接影响着后续的数据处理与型面质量评定。航空叶片通常是由叶身、榫根以及阻尼台构成,可用V型块、吸铁或专用夹具等装置对其进行测量定位,图3所示为叶片通过专用夹具的定位方式。目前基于叶片结构特征的定位夹具设计的理论和方法已较为成熟,单叶片的定位夹具设计可谓有规可循,但在实际应用中,应考虑定位夹具对具有相似外形的不同型号叶片的兼容性,其设计应该在保证定位精度的前提下尽量提高夹具的通用性[15],从而降低检测成本,这也是目前叶片工装夹具发展的主要方向。
叶片三坐标检测所获得的点云相对稀疏,具有测量点云与参考点云的初始姿态相似、位置相近的特点,其定位通常先在叶片特征面上采用6点定位法进行粗定位,其中最经典的是3-2-1定位法则,之后再进一步通过迭代运算对点云数据进行精密定位[16]。目前研究重点主要是如何快速精准地得到叶片测量坐标系与理论模型坐标系之间的变换矩阵。当前测点匹配运算通常采用遗传算法[17]或ICP(Iterative Closest Point)算法[18]进行计算。遗传算法的全局搜索能力强,能够得到全局最优解,但其对初始种群和遗传参数设置敏感,易出现收敛较慢或不收敛的情况,因此在具体匹配应用中常采用加速策略提高计算效率,这也是该方法目前发展的主要方向,如遗传算法结合最小二乘的求解方法。ICP算法对测量数据定位和轮廓误差评估意义重大,其基本原理是定义点-点的平方距离,并最小化该距离函数和,目前主要问题是点-点距离匹配对初值敏感,易陷入局部最优,导致精密定位和轮廓评估的不准确。尽管国内学者开展了ICP算法的改进研究,如陈志强[7]、蔺小军等[19]通过改进其目标函数,分别解决了叶片定位过程中区域公差约束问题和变形问题,但只要是点-点距离,仍然难以克服初值敏感性问题。国际上,文献[20]提出了TDM改进算法,一定程度上降低了对初始值的敏感性;此外文献[21]定义了点-曲面最近距离作为新的误差度量,构造了一种新的自适应距离函数,以此实现收敛速度和收敛稳定性的最优化,对叶片类复杂零件精密测量定位与轮廓评估具有重要意义。通过分析可知,针对有序点云测量数据的精确匹配技术仍有待进一步优化,其优化过程应综合考虑匹配算法的精度和效率这两个主要影响因素。

图3 叶片夹具定位Fig.3 Fixture positioning of blades
2.3 叶片坐标测量数据处理技术
叶片三坐标检测技术中的数据分析处理主要涉及到数据去噪、平滑、测头半径补偿等操作,其目的是为了降低数据的测量误差,提高后续评价参数计算的准确性。
叶片三坐标测量数据通常为有序点云,其数据去噪的方法相对成熟,可通过人机交互、弦高差法[22]、曲线检查法[23]以及平滑滤波[24]等方法实现。人机交互的方法适用于异常点与相邻点偏距较大的情况,其处理效率和自动化程度都较低,常用于点云的初步处理。弦高差法和曲线检查法由于原理简单、处理高效的特点在叶片去噪过程中有着广泛的应用,不过两种方法都对给定阈值的大小敏感,易出现丢失特征点的问题,对此,学者们提出了考虑测点邻域的去噪方法[25],该方法能准确地识别特征点和噪点,保证了点云数据特征的完整性。数据滤波主要是对隐含在测量数据中的噪声进行平滑处理,降低或者消除噪声对后续操作的影响,针对有序点云的滤波通常可采用标准高斯、中值或平均值滤波的方法,如文献[24]中采用高斯滤波的方法对扫描线结构的叶片点云数据进行了平滑去噪处理。
测头半径补偿处理是叶片三坐标测量数据处理的难点,这是由于补偿精度直接影响着叶片型面的评估,同时也影响着叶片型面的重构和再加工等操作。叶片进行等高测量时,由于叶身截面型线上各测点的法向实际属于三维范畴,按二维曲线进行补偿将引入补偿余弦误差,且测头半径越大,其余弦误差也越大。而根据理论点法矢方向进行采点时,由于实际型面与理论数模存在偏差,测点的实际高度就会与理论高度产生偏差,且其补偿曲线易出现“钝头”、“打结”的现象,两种补偿偏差如图4所示。针对上述情况,学者们提出了曲面拟合法进行半径补偿[26],其算法核心是先拟合出测头球心曲面,再通过曲面偏置运算得到实际测量曲面,进而通过映射得到补偿后的测量数据,该方法虽然消除了余弦误差带来的测量精度损失,但又引入了新的拟合误差和偏置误差。总而言之,现有的方法或多或少存在一些近似处理,且补偿算法的自适应性较差,针对不同类型的叶片其补偿精度波动较大,尤其是型面复杂的薄壁大扭曲叶片。
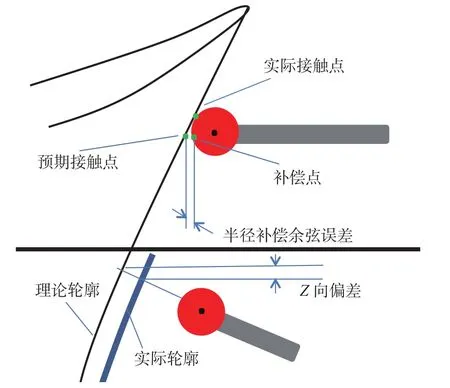
图4 测头半径补偿误差Fig.4 Compensation error of stylus radius
2.4 叶片型面评定技术
叶片型面质量的科学评定是检测的最终目的,在叶型的设计图纸中通常会给定评价参数的误差要求,包括截面型值点坐标、积叠点、缘半径、叶厚、弦长等特征参数要求,还包括叶片型面的倾斜度误差、弯曲度误差等位置度参数要求。通过对相关文献资料的调研,针对叶片截面的各特征评价参数的理论以及提取算法的发展已经较为成熟,在文献[27-29]中,详细介绍了叶片单截面各关键特征参数的提取方法,同时提出了包括倾斜度、弯曲度、扭曲度等多截面评价参数的提取算法,目前这些评定方法在叶片型面质量检测的过程中有着广泛的应用。但另一方面针对叶片整体型面评价参数的计算方法还有待进一步优化,这也是目前研究的重点方向。
叶片类自由曲面零件的曲面加工误差通常用形位误差中的面轮廓度误差来描述,其计算具有代表性的数学模型可分为两大类,一类是依照最小二乘法原则建立数学模型[30-31],将测量曲面与理论曲面的偏差转化成两个曲面上对应点距离的最小二乘法平方和,目前对该类方法的研究主要集中在对目标函数的优化和改进方面,如ICP算法、奇异值分解优化算法以及最速下降优化算法等。由于根据点对之间二范数计算出的点到曲面的距离模型精度较低,以及最小二乘法易收敛于局部最优解的原因,该类方法通常用于一般精度要求的曲面评定。另一类是基于最小区域原则建立的数学模型[32-33],其目标函数要求测量点到理论点距离中的最大值达到最小,可采用启发式的算法来对其进行优化,如遗传算法和粒子群算法等。在计算曲面轮廓度误差的过程中,计算测量数据到设计数模的距离是关键点和难点,对此,Zhu等[33]提出了利用有向距离函数来计算该距离的算法,但由于该算法计算过于复杂,在实际应用中通常利用一阶泰勒展开式来代替其距离函数,并用序列线性规划算法优化其目标函数。此外,Weber等[34]在分析现有最小二乘拟合算法和最小区域公差评价方法缺点的基础上,提出了一种通用的基于线性逼近技术的形状误差评价方法,常用在复杂曲面零件表面加工质量的检测中。总的来说,目前针对叶片类复杂自由曲面的误差评定,尚未形成一套完整、系统的评价方法,且多数误差评定方法主要停留在截面曲线的层面,针对叶片型面的误差评定算法还需不断完善和改进。
3 叶片坐标检测技术发展趋势
通过分析叶片三坐标检测技术所存在的问题,并且结合市场需求以及当前技术环境,可以得出叶片接触式的坐标检测技术正朝着智能化、复合化和网络化的方向发展,如图5所示。
(1)检测过程智能化。
叶片检测的智能化主要是检测过程与检测分析的智能化,包括了叶片的自动装夹与拆卸、叶片的原位测量、测量过程的自动化、测量策略自主化生成、测量测评报告的智能生成等,融入机器人技术、集成化以及人工智能、专家系统等技术,实现测量硬件与软件的智能化,能够有效消除叶片测量过程中人为因素的影响。
(2)检测方式复合化。
在众多叶片测量技术手段中接触式的坐标测量技术仍是目前精度最高的一种,但为了保证测量精度,要求其测量过程平稳,因此其测量效率往往低于非接触式测量技术。基于光学的非接触式测量由于测量效率较高的特点目前得到了迅速发展,尤其是激光测量技术在叶片检测中有着广泛的应用。在对叶片进行测量过程中,应综合考虑精度与效率的因素,不同的测量方式具有不同的优势,但也存在一定的局限性,为了适应不同测量工况和叶片应用对象,叶片检测在测量方式上呈现出复合化的趋势,这也是当前叶片测量设备朝着复合化方向发展的原因。通过应用多测头技术,支持接触式与非接触式融合的测量,能够显著提高测量效率,避免单一测量方式所引起的叶片局部区域失真。目前测量装备复合化已经有了良好的开端,少数国外企业已开发出了一些混合式测量设备。
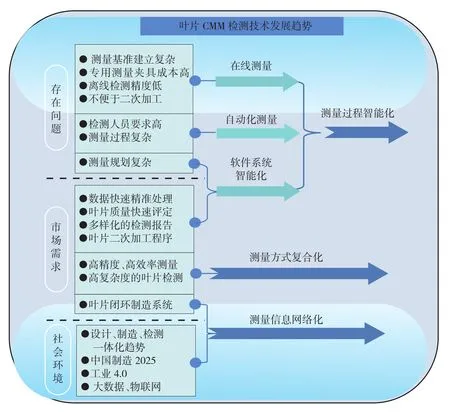
图5 叶片CMM检测技术发展趋势Fig.5 Development trend of CMM detection technology for blade
(3)检测信息网络化。
随着第四次工业革命的到来和“中国制造2025”的提出,工业制造行业向信息化、网络化方向发展。在现今物联网与大数据飞速发展的时代中,检测信息的网络化趋势必将推动叶片接触式坐标检测技术及设备的发展。在上下级多台测量机之间、设计人员与制造人员以及客户之间实现检测信息共享,不仅能够提高制造质量并减少制造耗费、降低生产成本,还能够在产品全周期获取叶片质量信息,实现质量追溯,及时改进制造工艺,实现航空发动机叶片的绿色智能化制造。例如,将测量技术与铣磨抛加工技术集成实现叶片自适应加工技术,通过将测量信息与铣磨抛等设备共享,根据检测结果自动生成叶片再加工方案以及相应程序,实现叶片的闭环模式加工,不仅可以大大缩短叶片制造周期,还能有效提高叶片加工精度与表面质量,最终有效保证叶片制造过程的稳定性与可靠性。
4 结论
目前我国在航空发动机研制领域虽然已经取得了有目共睹的进步,但仍与国际先进水平有着不小的差距。2016年5月,中国航空发动机集团正式成立,以研制大涵道大推力高性能高可靠度的国产航空发动机为目标,标志着我国迈出了建设航空强国的重要一步。叶片作为影响发动机性能的关键部件,对其制造质量实现有效控制和科学测评的叶片先进检测技术已经成为航空发动机研制过程中的一项关键技术。通过对航空叶片三坐标测量技术国内外现状的分析可以看出,虽然国内做了很多研究工作,开发了一些测量设备和软件系统,但是还有待于进一步完善和改进,主要在设备的稳定性、测量精度与效率以及叶片测量分析软件的准确性及智能化程度等方面相对于国外仍有一定差距。针对叶片坐标测量过程中的测量规划、精密定位等关键技术问题仍没有完全解决,从而制约了叶片型面测量精度与测量效率的提高。同时可以看出,为了提升航空发动机的性能,保证叶片型面制造质量,推动叶片的高精度、高效率测量,航空发动机叶片的三坐标检测技术必将向着智能化、复合化、网络化的方向发展。
[1] HUANG J, WANG Z, GAO J, et al. Overview on the profile measurement of turbine blade and its development[J]. Proceedings of SPIE-the International Society for Optical Engineering, 2010, 7656(2): 2-3.
[2] 史小强, 吴宝海, 张定华. 航空发动机叶片加工质量检测技术发展现状与趋势[J]. 航空制造技术, 2015(12): 80-84.
SHI Xiaoqiang, WU Baohai, ZHANG Dinghua. Development tendency of inspecting for aeroengine blade[J]. Aeronautical Manufacturing Technology, 2015(12): 80-84.
[3] ROBERT J H, PAULO H P. Coordinate measuring machines and systems[M]. 2nd ed. Boca Raton: CRC Press , 2016:18-21.
[4] CHANG H C, LIN A C. Automatic inspection of turbine blades using a 3-axis CMM together with a 2-axis dividing head[J]. The International Journal of Advanced Manufacturing Technology, 2005, 26(7): 789-796.
[5] 汪哲. 整体叶轮叶片型面几何误差分析技术研究[D]. 南京:南京航空航天大学, 2014.
WANG Zhe. Research on geometrical error analysis of blades on monolithic impeller[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.
[6] 席平, 孙肖霞. 基于CAD模型的涡轮叶片误差检测系统[J].北京航空航天大学学报, 2008, 34(10): 1159-1162.
XI Ping, SUN Xiaoxia. Error analysis system of turbine blade based on CAD model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(10): 1159-1162.
[7] 陈志强, 张定华, 金炎芳,等. 基于测量数据的叶片截面特征参数提取[J]. 科学技术与工程, 2007, 7(9): 1972-1975.
CHEN Zhiqiang, ZHANG Dinghua, JIN Yanfang, et al. Crosssectional feature parameter extraction of blade based on measurement data[J]. Science Technology and Engineering, 2007, 7(9): 1972-1975.
[8] PAHK H J, KIM Y H, HONG Y S, et al. Development of computeraided inspection system with CMM for integrated mold manufacturing[J]. CIRP Annals-Manufacturing Technology, 1993, 42(1): 557-560.
[9] KOSTRES M. Curvature-dependent parameterization of curves and surfaces[J]. Computer-Aided Design, 1991, 23(8): 569-578.
[10] 汪文虎, 赵德中, 崔康, 等. 航空发动机叶片型面三坐标测量方法: CN103411574 A[P]. 2013-11-27.
WANG Wenhu, ZHAO Dezhong, CUI Kang, et al. Three coordinate measuring method for aeroengine blade surface: CN103411574 A[P]. 2013-11-27.
[11] 蔺小军, 任军学, 李宜明, 等. 航空发动机叶片型面流道线测量路径规划方法: CN102323962A[P]. 2012-01-18.
LIN Xiaojun, REN Junxue, LI Yiming, et al. A path of flow channel line planning method for aeroengine blade surface measurement:CN102323962A[P]. 2012-01-18.
[12] 刘达新, 赵韩, 董玉德, 等. 三坐标测量机无碰撞检测路径的生成[J]. 计算机辅助设计与图形学学报, 2009, 21(6): 804-811.
LIU Daxin, ZHAO Han, DONG Yude, et al. Collision-free inspection path generation for coordinate measuring machines[J]. Journal of Computer-Aided Design & Computer Graphics, 2009, 21(6): 804-811.
[13] REDON S, KIM Y J, LIN M C, et al. Interactive and continuous collision detection for avatars in virtual environments[C]// Proceedings of IEEE Virtual Reality, Chicago:IEEE, 2004: 117-283.
[14] LIN Y J, MURUGAPPAN P. A new algorithm for determining a collision-free path for a CMM probe[J]. International Journal of Machine Tools & Manufacture, 1999, 39(9): 1397-1408.
[15] LIVINGSTON J T, HOLMES W B, SMETHERS F, et al. Jig and fixture for wind turbine blade: US20110030183[P]. 2011-02-10.
[16] HSU T H, LAI J Y, UENG W D, et al. An iterative coordinate setup algorithm for airfoil blades inspection[J]. The International Journal of Advanced Manufacturing Technology, 2005, 26(7): 797-807.
[17] 廖平, 王建录. 基于遗传算法的机械零件形位误差评定[M].北京: 化学工业出版社, 2012: 188-191.
LIAO Ping, WANG Jianlu. Form and position errors evaluation of mechanical parts based on genetic algorithm[M]. Beijing: Chemical Industry Press, 2012: 188-191.
[18] CHETVENRIKOV D, SVIRKO D, STEPANOV D, et al.The trimmed iterative closest point algorithm[C]// Proceedings of 16th International Conference on Pattern Recognition. Quebec: IEEE Computer Society, 2002: 30545.
[19] 蔺小军, 单晨伟, 王增强, 等. 航空发动机叶片型面三坐标测量机测量技术[J]. 计算机集成制造系统, 2012, 18(1): 125-131.
LIN Xiaojun, SHAN Chenwei, WANG Zengqiang, et al. Measurement techniques of coordinate machine for blade surface of aeroengine[J].Computer Integrated Manufacturing Systems, 2012, 18(1): 125-131 .
[20] POTTMANN H, HUANG Q X, YANG Y L, et al. Geometry and convergence analysis of algorithms for registration of 3D shapes[J].International Journal of Computer Vision, 2006, 67(3): 277-296.
[21] LI W L, YIN Z P, HUANG Y A, et al. Three-dimensional point-based shape registration algorithm based on adaptive distance function[J]. IET Computer Vision, 2011, 5(1): 68-76.
[22] LEE K H, WOO H, SUK T. Data reduction methods for reverse engineering[J]. The International Journal of Advanced Manufacturing Technology, 2001, 17(10): 735-743.
[23] 金涛, 陈建良, 童水光. 逆向工程技术研究进展[J]. 中国机械工程, 2002, 13(16): 1430-1436.
JIN Tao, CHEN Jianliang, TONG Shuiguang. Research progress of reverse engineering technology[J]. China Mechanical Engineering, 2002,13(16):1430-1436.
[24] HUANG M C, TAIC C. The preprocessing of data points for cue fining in reverse engineering [J]. The International Journal of Advanced Manufacturing Technology, 2000, 16(9): 635-642.
[25] 汪晓妍, 钱李勇, 杨延红, 等. 一种点云噪声点去除方法:CN103559689A[P]. 2014-2-5.
WANG Xiaoyan, QIAN Liyong, YANG Yanhong, et al. Method for removing noise points of point cloud: CN103559689A[P]. 2014-02-05.
[26] MAYER J R R, MIR Y A, TROCHU F, et al. Touch probe radius compensation for coordinate measurement using Kriging interpolation[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture, 1997, 211(1):11-18.
[27] ZHOU L P. A case study of blade inspection based on optical scanning method[J]. International Journal of Production Research, 2015,53(7): 2165-2178.
[28] LI W L, XIE H, LI Q D, et al. Section curve reconstruction and meancamber curve extraction of a pointsampled blade surface[J]. Plos One,2014, 9(12): 0115471.
[29] 马雯琦. 航空发动机叶片截面特征参数提取技术研究[D].天津: 天津大学, 2014.
MA Wenqi. Research of the aero engine blade cross-sectional feature parameters extraction[D]. Tianjin: Tianjin University, 2014.
[30] YAU H T. Evaluation and uncertainty analysis of vectorial tolerances[J]. Precision Engineering, 1997, 20(2): 123-137.
[31] 何改云. 形位误差的逼近原理及算法研究[D]. 天津: 天津大学, 2006.
HE Gaiyun. Research on the approach theory and algorithm for evaluating geometrical errors[D]. Tianjin: Tianjin University, 2006.
[32] WEN X, ZHAO Y, XU Y, et al. Quasiparticle swarm optimization for cross section linear profile error evaluation of variation elliptical piston skirt[J]. Mathematical Problems in Engineering, 2012,2012(3): 761978.
[33] ZHU L M, ZHANG X M, DING H, et al. Geometry of signed point-to-surface distance function and its application to surface approximation[J]. Journal of Computing & Information Science in Engineering, 2010, 10(4): 819-829.
[34] WEBER T, MOTAVALLI S, FALLAHI B, et al. A unified approach to form error evaluation[J]. Precision Engineering, 2002, 26(3):269-278.
