灵活运用乘法公式

朱适宜

灵活运用乘法公式

朱适宜

在“整式乘法与因式分解”这一章里我们学到的乘法公式有：完全平方公式：（a+b）2=a2+2ab+b2，（a-b）2=a2-2ab+b2.平方差公式：

（a+b）（a-b）=a2-b2.

那么对于这些公式，我们怎样才能做到灵活运用呢？下面和大家一起来分享一下.

一、完全平方公式

例1计算（a+b+c）2.

解法一：

解法二：

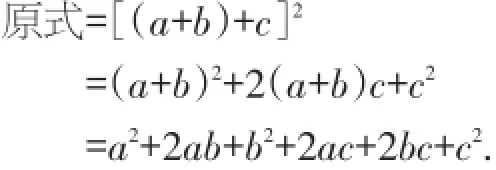
【说明】解法一是根据多项式与多项式相乘的法则：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加；解法二是利用整体思想将a+b看成整体，直接套用完全平方公式展开的.

例2若a是一个数，且4x2+axy+9y2是一个完全平方式，则a=.

解：±12.

【说明】本题考查的是完全平方式，完全平方公式展开后右边的形式a2+2ab+b2叫完全平方式，即两项的平方和加上或者减去两项乘积的2倍.这里可以确定两项的平方分别是4x2和9y2，则这两项分别是2x和3y，两项积的2倍是12xy，前面的符号可以是加号也可以是减号.所以答案是±12.

例3若2a2-2ab+b2+4a+4=0，求ab的值.

解：由题意知：a2-2ab+b2+a2+4a+4=0，

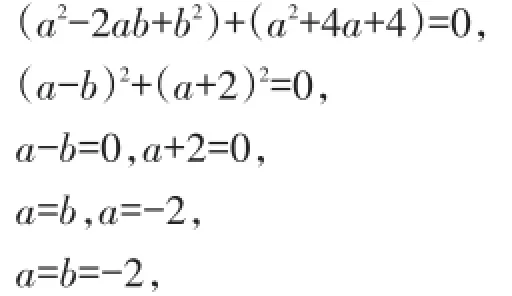
ab=（-2）-2=0.25.

【说明】本题由一个方程，求出两个未知数，所以这个方程一定是特殊的方程，结合已知条件可知：可以通过凑完全平方达到解决问题的目的，将2a2分成a2+a2，一个a2和-2ab，b2凑成（a-b）2，另一个a2和4a，4凑成（a+2）2，再根据平方具有非负性，得到两者均为0，从而求得a与b的值，最后代入求值.

二、平方差公式

例4计算（x+y+4）（x-y-4）.

解法一：

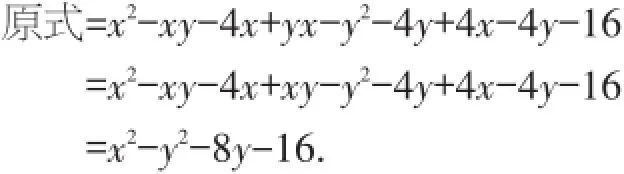
解法二：

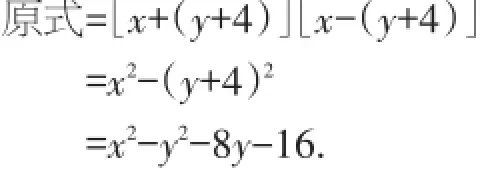
【说明】解法一是根据多项式与多项式相乘的法则：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加；解法二是利用整体思想将y+4看成整体，先套用平方差公式，再套用完全平方公式展开.我们在处理时要先观察：找到相同的项和互为相反数的项.那么对于（a-b+c-d）（-a-b+c+d）应该怎样套用平方差公式呢？这里找到相同的项-b和+c，互为相反数的项是a与-a，-d与d，我们就将其变为［（-b+c）+（a-d）］·［（-b+c）-（ad）］=（-b+c）2-（a-d）2，套用完全平方公式算出结果即可.

例5计算（x-1）（x2+1）（x4+1）（x+1）.

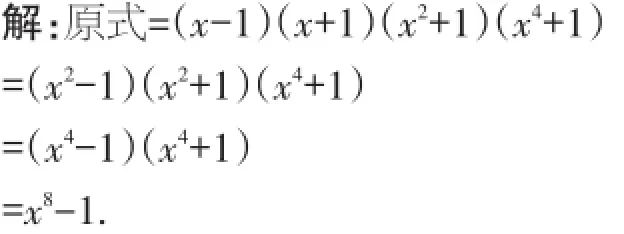
【说明】本题经过观察发现可以将x+1通过乘法交换律交换到前面，这样x-1和x+1就可以套用平方差公式进行简便计算，接着将上面所得的结果与x2+1再套用平方差公式进行简便计算，直至得到结果.

三、乘法公式的综合运用

例6计算（2y+1）2（2y-1）2.

解法一：

解法二：

【说明】本题的两种解法都采取了乘法公式，第一种先套用完全平方公式再套用平方差公式；第二种先利用乘法的交换律和结合律将其转化为［（2y+1）（2y-1）］2的形式，然后套用平方差公式，最后套用完全平方公式.两种方法比较，个人认为第二种在计算上更加简便.

例7解方程（2x-1）（1+2x）+3（x+2）（-2+ x）=7（x-1）2.

【说明】本题经过套用平方差公式和完全平方公式展开，发现关于x的二次项全部抵消，转化成了一个解关于x的一元一次方程的问题.这里需注意的是在套用平方差公式时，我们要看清楚相同的项以及互为相反数的项.

以上是我对运用乘法公式进行简便计算的一些想法和体会，相信你已经感受到了运用乘法公式进行计算的简便之处.其实在因式分解中，如果我们学会对乘法公式进行灵活运用，也可以大大地提高解题的速度和准确率，在以后的学习过程中，同学们要注意积累.

（作者单位：江苏省淮安外国语学校）

责任编辑：沈红艳李诗email：czsshy@126.com